Фрактальность природных объектов
СОДЕРЖАНИЕ: Такие объекты мы можем встречать в природе повсеместно: лист дерева, дерево, облако, сеть кровеносных сосудов человека и т дГОУ Гимназия №1505
«Московская городская педагогическая гимназия-лаборатория»
Реферат
Фрактальность природных объектов
Автор : ученица 9 класса «Б»
Фокин Фёдор
Руководитель: Ветюков Д.А.
Москва
2012
Оглавление
1. Введение………………………………………………………………………………3
2.Основная часть………………………………………………………………………...4
2.1. Виды математических фракталов
а)Геометрические………………………………………………………………..4
б)Алгебраические………………………………………………………………..4
в)Аттракторы. Странные аттракторы…………………………………………..5
г) Стохастические………………………………………………………………..7
2.2 Биологические фракталы
а) Древние фрактальные животные…………………………………………….8
б) Фрактальность современных живых организмов………………………….9
2.3 Механизм возникновения фрактальных структур в математике.
Возможность кодирования фрактала при помощи малого кода…………………….11
3. Заключение…………………………………………………………………………...12
4.Литература…………………………………………………………………………….12
1. Введение
Существует всего 2 типа фракталов: математические и физические (биологические). Математический фрактал (лат. fractus — дроблёный) — бесконечно самоподобная геометрическая фигура, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком. Реальные объекты, в частях которых можно заметить фрактальную структуру (т.е. самоподобие, простирающееся до очень мелких структур этих объектов) называются физическими фракталами. Их отличие от математических в том, что их самоподобие конечно, так как не существует тел с бесконечно малыми размерами элементов (размеры тел, по крайней мере, ограничены размерами атомов). Такие объекты мы можем встречать в природе повсеместно: лист дерева, дерево, облако, сеть кровеносных сосудов человека и т.д.
Наше предположение состоит в том, что наличие самоподобия (фрактальности) у живых организмов может являться принципиальным моментом организации живой материи. Развитие от простого к сложному, когда более мелкие структуры повторяют более крупные – это способ компактной схемы построения живого. В такой схеме на каждом уровне масштаба применяется один и тот же алгоритм построения. Целью нашего реферата является выяснение способов организации фрактальных структур (способов их конструирования в случае математических фракталов) и попытке осмысления их назначения в процессе развития живого организма.
Хотя в настоящее время тема фракталов достаточно популярна, назначение фрактальных структур у живых организмов освещена в литературе крайне скудно, поэтому основным источником информации для нашей работы является информация найденная в Интернете.
В начале основной части приведена информация о различных видах математических фракталах их особенностях и характеристиках. Затем мы остановимся на описании биологических объектов, имеющих фрактальную структуру. После этого мы попытаемся проанализировать алгоритмы конструирования фракталов в математике и природе, в заключение попытаемся сформулировать преимущества фрактальной организации в живых организмах.
2. Основная часть
2.1. Виды математических фракталов
а) Геометрические фракталы
«Именно с этого вида фракталов началась история фракталов. Этот тип фракталов получается путем простых геометрических построений. Обычно при построении этих фракталов поступают так: берется набор отрезков, на основании которых будет строиться фрактал. Далее к ним применяют набор правил, который преобразует их в какую-либо геометрическую фигуру. Далее к каждой части этой фигуры применяют опять тот же набор правил. С каждым шагом фигура будет становиться все сложнее и сложнее, и если мы проведем бесконечное количество преобразований, то получим геометрический фрактал».1

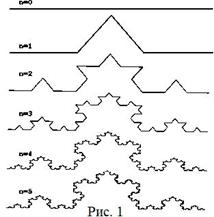
Рис 1. Снежинка Коха
«Из геометрических фракталов очень интересным и довольно хорошо известным является снежинка Коха. Строится она на основе равностороннего треугольника, каждая линия которого заменяется на 4 линии длиной в ![]() исходной. Таким образом, с каждой итерацией длина кривой увеличивается на треть. И если мы сделаем бесконечное число итераций, то получим нужный фрактал, то есть снежинку Коха бесконечной длины».[1]
исходной. Таким образом, с каждой итерацией длина кривой увеличивается на треть. И если мы сделаем бесконечное число итераций, то получим нужный фрактал, то есть снежинку Коха бесконечной длины».[1]
б) Алгебраические фракталы
Это самая крупная группа фракталов. Получают их с помощью нелинейных функций (функций, аргументы которых очень сильно влияют на ее значение). Очень малое изменение аргументов приводит к сильному изменению значения функции. Наиболее хорошо известны функции двух аргументов (например, x,y). В этом случае, если сопоставить со значениями этой функции различные цвета - мы получим фрактальную картинку в этих координатах. Из подобных фракталов наиболее хорошо известен фрактал Мандельброта.
Алгебраические фракталы тесно связаны с рядом физических нелинейных систем (систем, поведение которых очень чувствительно к малейшему изменению некоторых параметров). Геометрический объект, описывающий такие системы, называется странным аттрактором. Рассмотрим странные аттракторы подробнее.
в) Аттракторы. Странные аттракторы.
Пусть имеется нелинейная динамическая система, обладающая несколькими устойчивыми состояниями. Примером такой системы может быть магнитик на нитке, в случае если сбоку прикреплен еще один магнит. Магнитик может повиснуть в нижней точке, а может зависнуть сбоку, притягиваясь ко второму магниту. В таком случае у данной системы имеется два устойчивых состояния. Каждое из этих устойчивых состояний называется аттрактором. Математическое определение аттрактора следующее:
Аттрактор (англ. attract — привлекать, притягивать) — компактное подмножество фазового пространства динамической системы, все траектории из некоторой окрестности которого стремятся к нему при времени, стремящемся к бесконечности.
Фазовое пространство динамической системы:
Система - это какие-либо тела, которые мы назвали системой.
Точка фазового пространства – набор характеристик системы, которые полностью эту систему описывают.
Фазовое пространство – совокупность всех возможных наборов характеристик системы.
Каждый аттрактор обладает некоторой областью начальных состояний, из которых система обязательно попадет в него. В нашем примере имеется две области: если отпустить магнитик в одной области он притянется к одному аттрактору, если в другой - он притянется к другому. Если добавить еще два значения начальной скорости магнитика, мы получаем четырехмерное фазовое пространство, имеющее также две области притяжения к одному и другому аттрактору.
Таким образом, фазовое пространство системы разбивается на области притяжения аттракторов. Если фазовым является двухмерное пространство, то окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы.
Приведем еще один аттрактора.
Имеется шарик на пружинке. Его движение определяется только двумя числами характеризующими начальное состояние системы: растяжением пружинки и скоростью шарика. В этом случае фазовое пространство имеет два измерения: длину пружинки и скорость шарика. Аттрактором в этом случае будет точка 0,0, т.е. пружинка не растянута, а скорость равна нулю.
Странный аттрактор — это аттрактор, имеющий два существенных отличия от обычного аттрактора: траектория движения у такого аттрактора непериодическая (она не замыкается), режим функционирования неустойчив (малые отклонения нарастают).
Динамика на странных аттракторах часто бывает хаотической: прогнозирование траектории, попавшей в аттрактор, затруднено, поскольку малая неточность в начальных данных через некоторое время может привести к сильному расхождению прогноза с реальной траекторией. Непредсказуемость траектории в динамических системах называют динамическим хаосом. Это явление также называют эффектом бабочки, подразумевая возможность преобразования слабых турбулентных потоков воздуха, вызванных взмахом крыльев бабочки в одной точке планеты в мощное торнадо на другой её стороне вследствие многократного их усиления в атмосфере за некоторое время.
Область притяжения к странному аттрактору является фрактальным объектом.
Попытаемся разобраться, почему возникает фрактальность областей притяжения к странным аттракторам. Разберемся для этого со следующим примером:
«Если раскачивать металлический маятник над тремя магнитами, лежащими в вершинах правильного треугольника симметрично от точки подвеса магнита и отмечать разными цветами области притяжения к каждому из них, то непосредственно вокруг самих магнитов будет область, полностью залитая цветом, соответствующим его области притяжения. Но если мы также попробуем точно определить границы областей притяжения, то у нас это не получится. Области притяжения на границах будут смешаны так, что в зоне притяжения одного магнита окажется участок области притяжения другого, в нём небольшой участок притяжения снова к первому. Мы обнаружим и такие участки, где все три цвета бесконечно перемешаны, так что там невозможно найти область притяжения одного магнита, которая не соприкасалась бы с зонами притяжения обоих других магнитов одновременно. Границы притяжения между магнитами будут фрактальны».[2]

Рис 3. Визуализация фрактальной границы между областями притяжения маятника к трём магнитам.
г) Стохастические фракталы
Стохастичность (греч. — цель или предположение) означает случайность, поэтому стохастическими называются алгебраические или геометрические фракталы, при построении которых случайным образом изменяются какие-либо параметры. С помощью компьютера такие структуры строить достаточно просто: надо просто задать последовательности случайных чисел и настроить соответствующий алгоритм. При этом получаются объекты, очень похожие на природные. Например, несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.
Итак, математические фракталы можно разделить на 2 группы:
1. Фракталы, в основе структуры которых лежит функция, т.е. взаимодействие параметров друг с другом.
2. Фракталы, в основе которых лежит четкая зависимость следующих его элементов от уже построенных, а итоге получается практически одинаковая структура на ее всех уровнях.
В обеих группах возможно случайное варьирование некоторыми параметрами фрактала.
2.2 Биологические фракталы. Природные фракталы.
а) Древние фрактальные животные
Организмы в ходе эволюции усложнялись. Возможно, наиболее простые в древности состояли из одинаковых клеток с фрактальной организацией.
«В прошлом фрактальные животные располагались на глубине нескольких тысяч метров на дне океана. Они не считаются растениями, так как на такой глубине света не хватило бы на процесс фотосинтеза. Предположительно, они жили за счет растворенного в океанских водах углерода и других питательных веществ, которые они поглощали всем телом. Они не могли передвигаться, не имели рта и мышц и являются самыми древними многоклеточными организмами на Земле».3
Одной из наиболее специфических особенностей их строения является их способ формировании тел. Они обладали очень простой структурой ветвления, так как их создание занимало 6-8 «генетических команд», следовательно, они использовали фрактальный способ построение тел.
«Фрактофус – одна из наиболее распространенных окаменелостей в Великобритании, свидетельствующих о существовании в прошлом этих животных. Он состоял из ветвящихся элементов, по 20 с каждой стороны. Каждая ветвь в точности повторяла своего родителя, начиная с микроскопического уровня. Это был простой, но очень эффективный способ построения тела. Благодаря тонко разделенным ветвям у организма была большая по площади поверхность, что позволяло ему впитывать питательные вещества напрямую, не имея рта и пищеварительного тракта.
Используя фрактальный способ построении тела животные впервые в истории жизни на Земле стали крупными. Фрактальный способ оказался полезным для того, чтобы ранние организмы начали развиваться, потому что для создания одной особи требовался минимум генетической информации. Фрактальные организмы исчезли после нескольких миллионов лет своего существования».
Таким образом, Дэвид Аттенборо делает очень важное с нашей точки зрение предположение, заключающееся в том, что фрактальная структура у древних животных позволяла очень просто кодировать информацию об организме. Даже такое примитивное живое существо состояло из многих миллионов живых клеток. Фрактальная структура позволяла организовывать положение этих клеток в пространстве при помощи нескольких простых команд.[3]
б) Современные фрактальные организмы
С течением эволюции полностью фрактальные организмы прекратили свое существование, но фрактальность отдельных структур осталась. В настоящее время фрактальность можно встретить повсеместно.
Растения. Жилка листа состоит из ксилемы (древесина) и флоэмы (луб). Ксилема выполняет функцию транспорта воды и минеральных веществ от корня к листьям (для фотосинтеза), а флоэма транспортирует органические вещества (полученные в результате фотосинтеза) от листьев к корню.
У двудольных и однодольных растений жилкование листа разное. У двудольных растений жилкование подразделяется на пальчатое (клен, ревень) и перистое (дуб, осина, липа) Наиболее яркие фрактальные свойства проявляются при перистом типе жилкования. Для фотосинтеза растению нужна вода, а такой тип жилкования обеспечивает каждую клетку листа достаточным количеством воды, что способствует более быстрому протеканию химических процессов, в том числе и фотосинтеза.
Фрактальность можно наблюдать и у дихотомического ветвления побегов.
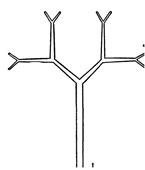
«Ветвление имеет большое значение в жизни растения, увеличивая ассимилирующую поверхность (ассимиляция - совокупность процессов синтеза) и улучшая, таким образом, его питание. Вместе с этим нарастает и общее количество меристемы (образовательной ткани). Так как меристема образуется не сразу, растение всегда имеет запас этой ткани, используемые не только на естественное увеличение мощности побеговой системы, но и на восстановительные процессы после какого-либо повреждения».[4]
Животные. « Любой орган животного в норме также имеет квазифрактальную (почти фрактальную) структуру, даже если внешне не выглядит фрактализованным. Каждая живая клетка многоклеточного образования должна непрерывно потреблять кислород, питательные вещества, избавляться от углекислого газа и продуктов обмена. Одним словом, она должна достаточно свободно контактировать с внешней средой, чтобы обмениваться с ней веществом и энергией. Для внутренней среды организма функцию внешней среды выполняет кровеносная система, она осуществляет газообмен, обмен питательными веществами, информационными молекулами, управляющими деятельностью клеток, в кровь сбрасываются продукты обмена. Обмен между кровеносной системой и внутренней средой организма осуществляется через двумерную поверхность эндотелия капилляров, то есть через плоскость. Чем больше площадь обмена, то есть площадь эндотелия капилляров, тем обмен интенсивнее, тем большее количество продуктов обмена может быть перенесено через неё за единицу времени. Наиболее эффективно заполнить трёхмерный объём двумерной плоскостью, как упоминалось ранее, можно фрактальной укладкой этой плоскости внутри заданного объёма. Фрактальная укладка позволяет достичь изгибами или ветвлениями фрактальной самоподобной двумерной структуры, заполняющей трёхмерное пространство, каждой клетки, каждого участка внутри заполняемого ею объёма. Кровеносная система опутывает квазифрактальной капиллярной сетью внутренний объём каждого органа организма животного так, что в непосредственной близости от каждой клетки находится капилляр, через который происходит обмен клетки с окружающей средой. Кровеносная система организма и каждого отдельного органа квазифрактальна. Но, если рассматривать кровеносную систему как внешнее, относительно самого органа, пространство, например, если удалить из органа кровеносную систему, то и сам орган, разделённый на сегменты пространством, занимаемым ранее кровеносной системой, будет также представлять собой квазифрактал. Обобщая, можно сказать, что структура всякого достаточно большого многоклеточного органа всегда квазифрактальна, так как только через квазифрактальную организацию можно добиться эффективного обмена каждой клетки органа с окружающей средой».[5]
2.3 Механизм возникновения фрактальных структур в математике. Возможность кодирования фрактала при помощи малого кода.
Итак, существует 2 основных группы математических фракталов: алгебраические, основанные на определенной зависимости, и геометрические, суть которых в многократном повторении определенных алгоритмов при построении фрактала, причем эти алгоритмы повторяются все в меньшем масштабе. Оба эти принципа теоретически могут реализовываться в природе. Алгебраический механизм образования фрактальных структур в живых организмах может возникать из-за их чрезвычайной чувствительности ко многим факторам (любой живой организм является нелинейной системой). Но мы не собираемся глубоко изучать алгебраически фракталы, так как для этого у нас не хватает, ни математических, ни биологических знаний.
Рассмотрим более подробно второй способ образования фрактальных структур – геометрический. Сложная структура живых организмов в процессе роста требует последовательного разворачивания. Такое разворачивание можно организовать по алгоритму создания геометрических фракталов. Такая организация дает два основных преимущества: с одной стороны, простота организации, с другой – возможность описать сложную систему несколькими командами (алгоритмом) ее создания.
Как уже было сказано, фрактальные объекты примечательны тем, что они кодируются при помощи всего нескольких операций, которые и описывают самоподобие объекта. Значит и в случае биологического фрактального организма генетическая информация, достаточная для разворачивания такой системы, будет состоять всего из нескольких команд. В природных фрактальных объектах можно заметить, что самоподобие строится от маленьких элементов к большим.
Рассмотрим, как могут выглядеть такие «генетические команды» в простой математической модели развития такого фрактального объекта.
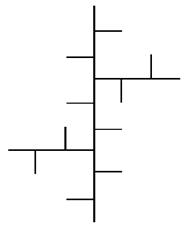
Рис.4
Рассмотрим, как можно запрограммировать построение фрактальной
структуры, изображенной на рисунке 4.(ветвление повторяется на более мелком уровне).
1. Взять отрезок минимальной длины.
2. Начать увеличивать имеющуюся фигуру.
3. При достижении какого-либо элемента фигуры длины равной трем
минимальным, построение двух отрезков, направленных перпендикулярно
исходному из точек, делящих его на 3 равных части из частей фигуры, появившихся в последнем сделанном пункте 3.
4.Перейти к пункту 2.
На наш взгляд именно этот способ построения можно использовать при моделировании развития живых организмов, например, древнего фрактофуса.
3. Заключение
В данной работе мы изучили принципы организации фракталов, как эти принципы соотносятся с живыми организмами. И выдвинули гипотезу, что фрактальная организация позволяет компактно хранить информацию, и быстро разворачивать крупные системы, что
теоретически организмы могут использовать геометрический фрактальный способ роста, так как это способствует хранению меньшего количества информации в ДНК.
4. Источники
1. Режим доступа: http://sakva.net/old/fractals_rus/. Данные соответствуют 14.04.12.
2. Каретин Ю. А. Синергетика: курс лекций для биологов. – ДВГУ, 2007.
3. Научно-популярный фильм «Первая жизнь с Дэвидом Аттенборо», 2010.
4. Л. И. Лотова. Ботаника. Морфология и анатомия высших растений. - М.: Эдиториал УРСС, 2001.
[1] Режим доступа: http://sakva.net/old/fractals_rus/. Данные соответствуют 14.04.12.
[2] Каретин Ю.А. Синергетика: курс лекций для биологов. – ДВГУ, 2007. С.110-111
[3] Расшифровка текста научно-популярного фильма «Первая жизнь с Дэвидом Аттенборо», 2010, сделана автором реферата.
[4] Л. И. Лотова Ботаника. Морфология и анатомия высших растений. М.: Эдиториал УРСС, 2001. С. 138.
[5] Каретин Ю.А. Синергетика: курс лекций для биологов. – ДВГУ, 2007. С. 131-132