Варіаційні ряди, їх види, правила побудови, роль та значення в аналізі статистичних даних
СОДЕРЖАНИЕ: Статистичний ряд розподілу та варіаційні ряди. Приклади побудови та графічного зображення рядів розподілу, полігон, гістограма, кумулята. Криві розподіли та їх види. Суть статистичного зведення, класифікація та агрегатування матеріалів спостереження.МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Кафедра економіки
КУРСОВА РОБОТА
зі статистики на тему
“Варіаційні ряди, їх види, правила побудови, роль та значення в аналізі статистичних даних”
Суми 2009
Зміст
Вступ
1. Статистичний ряд розподілу
2. Варіаційні ряди
3. Приклади побудови та графічного зображення рядів розподілу
3.1 Полігон. Гістограма
3.2 Кумулята
3.3 Криві розподіли та їх види
4. Практичне завдання
Висновок
Перелік посилань
Додатки
Вступ
Статистика – наука, яка вивчає кількісну сторону масових суспільно-економічних явищ та процесів у нерозривному зв’язку з їх якісною характеристикою в умовах визначеного місця і часу.
Статистика має низку суттєвих специфічних особливостей, що відрізняють її від інших суспільних наук. Ці особливості пов’язані з пізнанням суспільно-економічних явищ і процесів, тобто характеристикою кількісної їх визначеності, наприклад, характеристика зміни чисельності населення, його структури, випуску продукції в різних галузях суспільного виробництва, чисельності робітників, зміни показників ефективності видів економічної діяльності, співвідношення між обсягом виробленої і реалізованої сільськогосподарчої продукції тощо[ 1,10].
Вивченням економічного і соціального розвитку країни, окремих її регіонів, галузей, об’єднань, фірм, підприємств займаються спеціально створені для цього органи, сукупність яких називається статистичною службою. В Україні функції статистичної служби виконують органи державної статистики і органи відомчої статистики.
Централізоване керівництво веденням статистики в нашій країні здійснює спеціально уповноважений центральний орган виконавчої влади в галузі статистики, який утворюється відповідно до статті 106 Конституції України. З 1997 року функції державного управління у сфері статистики здійснює Державний комітет статистики України (Указ Президента України “Про утворення Державного комітету статистики України” від 29.07.97 за № 734/97)[ 2,20].
Держкомстат України виконує роботу із збирання, опрацювання та аналізу науково обгрунтованих даних, що характеризують економічний і соціальний розвиток країни, процеси становлення багатоукладної економіки, хід виконання державних і регіональних програм, пов’язаних із рішенням важливих народногосподарських проблем.
Первинні статистичні дані, зібрані внаслідок статистичного спостереження, характеризують окремі одиниці досліджуваної сукупності і часто складні для розуміння. Для того, щоб вивчити характерні риси та істотні відмінності тих чи інших явищ, виявити закономірності їх розвитку, треба дані щодо кожного елементу сукупності систематизувати і обробити Цей етап статистичного дослідження називають статистичним зведенням.
Суть статистичного зведення полягає в класифікації та агрегатуванні матеріалів спостереження. Елементи сукупності об’єднуються за певними ознаками в групи, класи. типи, а інформація про них агрегується як у межах груп, так і в цілому по сукупності. Таким чином, статистичне зведення– це процес упорядкування, систематизації і наукової обробки первинного статистичного матеріалу для виявлення типових рис і закономірностей явищ і процесів, що вивчаються[ 2,47].
Складові елементи статистичного зведення:
Розробка програми систематизації та групування даних, вибір групувальних ознак і встановлення меж групування;
Статистичне групування;
Обгрунтування і розробка системи показників для характеристики груп і сукупності в цілому;
Визначення технологічних схем обробки інформації, типів ЕОМ, програмного забезпечення;
Безпосереднє зведення, узагальнення, розрахунок системи показників;
Викладення результатів зведення у вигляді рядів розподілу, статистичних таблиць і графіків.
Успішне вирішення завдань зведення можливе лише при науковому його обгрунтуванні і правильній організації. Зведення результатів статистичного спостереження має здійснюватись за заздалегідь складеною програмою. Залежно від завдання, поставленого перед конкретним дослідженням, програма встановлює групувальні ознаки, кількість і перелік груп, макети розроблюваних таблиць, а також перелік показників, які повинні бути визначені для характеристики кожної групи і сукупності в цілому. Такі характеристики можуть визначатись у формі абсолютних (підсумкових показників), середніх і відносних величин[ 2,48].
В даній курсовій роботі розглянемо роль та значення варіаційних рядів в аналізі статистичних даних, їх види, правила побудови. Використаємо матеріали конкретної статистики, розглянемо сільсько-господарське підприємство з даними про кількість працюючих на підприємстві та їх заробіток.
1. Статистичний ряд розподілу
Розглянемо такий складовий елемент статистичного зведення, як викладення результатів зведення і групування у вигляді рядів розподілу.
Статистичний ряд розподілу – це ряд, який характеризує розподіл одиниць сукупності по групах за будь-якою ознакою, різновидності якої розташовані у певному порядку. В статистиці ряди розподілу є найпростішим способом узагальнення статистичних даних.
Групувальними ознаками називають ознаки, які покладені в основу групування. За формою вираження групувальні ознаки можуть бути атрибутивними і кількісними. Атрибутивними називаються ознаки, які не мають кількісного вираження і реєструються у вигляді текстового запису. Число груп, на які поділяється досліджувана сукупність, визначається кількістю різновидів цієї ознаки. Так, групування населення за статтю дає дві групи – чоловіки і жінки, групування населення за рівнем освіти дає шість груп – повна вища, базова вища, професійно-технічна, повна загальна, базова загальна середня, початкова загальна.
Окремим видом атрибутивних групувань є групування за альтернативною ознакою, коли є лише два варіанти атрибутивної ознаки, причому один з них виключає інший. Наприклад, розподіл студентів на тих, хто одержує стипендію, і тих, хто її не одержує; підприємство може бути рентабельним, або збитковим.
Кількісні (варіюючі) ознаки – це ознаки, які набувають різних цифрових характеристик і виражаються числовими значеннями. Наприклад, розподіл робітників підприємства за віком, за стажем роботи, за розміром заробітної платні.
Наступним важливим кроком після визначення групувальної ознаки є розподіл одиниць сукупності на групи. Тут виникає питання щодо кількості груп і величини інтервалу. Здійснюючи групування за атрибутивними ознаками, питання про кількість груп не ставиться, оскільки їх стільки, скільки атрибутивних ознак.[ 3,55].
При групуванні за кількісними ознаками постає питання щодо кількості груп і інтервалів групування. Питання про кількість груп і величину інтервалу слід вирішувати залежно від багатьох обставин, насамперед відповідно до мети дослідження і діапазону варіації групувальної ознаки. Кількість груп пов’язано з обсягом сукупності. Тут немає чітко визначених наукових прийомів, які дозволяють вирішувати це питання при будь-яких обставинах. Кожного разу це завдання вирішується з урахуванням конкретних обставин. Однак, існує формула, запропонована американським вченим Стерджесом, за допомогою якої можна визначити кількість груп n, якщо відома чисельність сукупності N[ 2,55]:
n = 1 + 3,322 lg N (1)
Наприклад, при 200 одиницях сукупності число груп визначається таким чином:
n = 1 + 3,322 lg 200 =9.
За величиною розрізняють інтервали рівні і нерівні. Рівні інтервали застосовують тоді, коли зміни кількісної ознаки всередині сукупності відбуваються рівномірно. Розмір рівних інтервалів визначають за формулою:
h = (xmax-xmin)/n,
де h — величина інтервалу;
xmax— максимальне значення ознаки;
xmin — мінімальне значення ознаки;
n — кількість груп.
Таким чином, величина інтервалу залежить від кількості груп (n) і коливання досліджуваної ознаки. Чим ширший розмах коливання (xmax-xmin), тим більша величина h; чим більше n, тим менше h.
2. Варіаційні ряди
Ряди розподілу одиниць сукупності за ознаками, які мають кількісне вираження, називають варіаційними рядами. Варіаційні ряди дають можливість визначити характер розподілу одиниць сукупності за тією чи іншою кількісною ознакою. Варіаційні ряди розподілу залежно від групувальної ознаки поділяють на інтервальні та дискретні.
В інтервальних варіаційних рядах групувальна ознака може приймати любе значення (ціле, дрібне) в межах кожного інтервалу (наприклад, розподіл заробітної платні працюючих в організації, розподіл основних фондів підприємства тощо). Прикладом інтервального варіаційного ряду буде слідуючий розподіл 500 працівників сільськогосподарського підприємства за розміром місячної заробітної плати (табл.2.1).
Таблиця 2.1 Розподіл працівників сільськогосподарського підприємства за розміром місячної заробітної плати
|
Розміри заробітної плати, грн. |
Чисельність працівників |
|
| в абсолютних цифрах |
в % до підсумку |
|
| 1200-1400 |
10 |
2 |
| 1400-1600 |
30 |
6 |
| 1600-1800 |
50 |
10 |
| 1800-2000 |
60 |
12 |
| 2000-2200 |
145 |
29 |
| 2200-2400 |
110 |
22 |
| 2400-2600 |
80 |
16 |
| 2600-2800 |
15 |
3 |
| Разом |
500 |
100 |
Приведений варіаційний ряд показує, що найбільш багаточисельна група складається з працівників, заробітна плата яких є від 2000 до 2200 грн. у місяць. У групах вище та нижче цієї групи чисельність робітників зменшується, причому у групах з більш високою заробітною платою число робітників більше. Таким чином, число робітників у групах, заробітна плата яких є 2200 і вище, складає 41% (22+16+3), а в групах нижче 2000 грн. – 30% (2+6+10+12), а якщо взяти число працюючих в інтервалі місячної заробітної плати від 1800 до 2400 грн., то воно складає 63% усіх працівників (12+29+22).
В дискретних варіаційних рядах варіанти завжди мають значення цілих чисел (наприклад, тарифний розряд робітників, кількість марок автомобілів тощо). Таблицею 2.2 ілюструється дискретний ряд розподілу студентів фінансового факультету за курсами[ 2,58].
Таблиця 2.2 Розподіл студентівфінансового факультету ЛДФЕІ за курсами (станом на 01.01.2001 р.)
| Курс |
Кількість студентів |
| I |
175 |
| II |
200 |
| III |
184 |
| IV |
96 |
| V |
60 |
| Разом |
715 |
До основних елементів варіаційних рядів розподілу відносяться:
варіанти xi – числові значення кількісної ознаки в групуванні (перша графа таблиць), які можуть бути додатними, від’ємними, абсолютними, відносними;
частоти fi – значення окремих варіантів (друга графа);
частки i (третя графа).
У наведеній вище таблиці 2.1 (Розподіл робочих за розміром місячної заробітної платні) варіантою групувальної ознаки є розмір заробітної платні, який приведений у вигляді інтервалів (1200-1400, 1400-1600 і т. д.). Таким чином, перша варіанта (1200-1400) зустрічається в наведеному вище ряді 10 разів (її частота дорівнює 10), друга варіанта – 30 разів і т. д.
У таблиці 2.2 курси є варіантами, а кількість студентів — частотами.
Частоти, які відповідають певній ознаці, можуть подаватись як в абсолютних значеннях, так і у відносних, виражених коефіцієнтом або відсотком (часткою). Накопичену частоту (частку, i) називають кумулятивною.
Окрім зазначених елементів варіаційних рядів до їх характеристик можуть бути віднесені такі показники: щільність частоти (h – ширина інтервалу); накопичена частка. Такі показники використовуються при розгляді побудованих рядів розподілу.
3. Приклади побудови та графічного зображення рядів розподілу
Наочне представлення результатів спостереження та групування соціально-економічних явищ і процесів може бути надано на графіках. Статистичний графік– це масштабне зображення статистичних даних за допомогою ліній, геометричних фігур та інших наочних засобів. Графіки використовуються для характеристики зміни суспільних явищ і процесів у часі, дослідження структури та порівняння явищ, контролю виконання плану, зображення явищ у просторі та в інших випадках. Вони дають змогу візуальним способом охопити всю сукупність статистичних даних і скласти в цілому картину про вивчаєме явище чи процес. Наочне зображення досліджуваних даних сприяє кращому виявленню найхарактерніших зв’язків між факторами, дозволяє виявити тенденцію у зміні та розвитку окремих явищ. Значна роль графічної інформації у пропаганді передового досвіду, новітніх технологій, прогресивних тенденцій, в рекламних цілях тощо[ 3,62].
Особливе місце, у зв’язку із специфічністю, займає графічне зображення рядів розподілу. Такі графіки значно полегшують аналіз рядів розподілу, дозволяють отримати уявлення про форму розподілу. Варіаційний ряд можна зобразити у вигляді полігона і гістограми.
3.1 Полігон. Гістограма
Для графічного зображення дискретного варіаційного ряду використовують полігон розподілу. Його зображують у прямокутній системі координат, де на осі абсцис відкладають значення варіант x, а на осі ординат – частоти f. Одержані точки з координатами xi та fi з’єднують прямими лініями. Для замикання полігону кінцеві вершини з’єднують з точками на осі абсцис, які відстоять на одну поділку від xmax і xmin [ 3,65].
Графічне зображення інтервального варіаційного ряду будується у вигляді гістограми.
При побудові гістограмми для інтервального ряду з рівними інтервалами на осі x відкладаються межі інтервалів та, використовуючи відрізки, що представляють інтервали, як підстави, будують на них прямокутники з висотою, рівній частоті даного інтервалу.
На рис.3.1 представлена гістограмма наведеного вище (табл.2.1) розподілу робітників за розміром місячної заробітної плати.
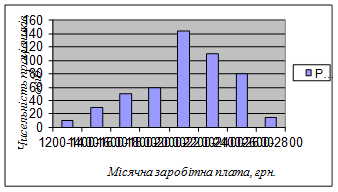
Рис. 3.1 Гістограма розподілу працівників сільськогосподарського підприємства за розміром заробітної плати
3.2 Кумулята
У практиці економічної роботи може виникнути потреба в перетворенні рядів розподілу у кумулятивні ряди, які будуються за накопиченими частотами (частками). На підставі таких рядів визначають структурні середні, вивчають процес концентрації досліджуваного явища. Накопичені частоти визначають шляхом послідовного додавання частот (часток) наступних груп. За даними кумулятивного ряду з накопиченими частотами (частками) можна побудувати графік у вигляді кумуляти (кривої сум). При графічному зображенні кумуляти накопичені частоти наносять на графічне поле у вигляді перпендикулярів на ось абсцис, які з’єднуються ломаною лінією[ 2,61].
Порядок побудови кумулятивного ряду розглянемо на прикладі (таблиця 3.1), використовуючі дані наведеної вище таблиці 2.1 (Розподіл працівників сільськогосподарського підприємства за розміром місячної заробітної платні):
Таблиця 3.1 Розподіл працівників сільськогосподарського підприємства за розміром місячної заробітної плати
| Розміри заробітної платні, грн. |
Чисельність працівників |
Кумулятивна (накопичена) чисельність працівників |
||
| в абсолютних цифрах |
в % до підсумку |
|||
| 1200-1400 |
10 |
2 |
10 |
|
| 1400-1600 |
30 |
6 |
40 |
|
| 1600-1800 |
50 |
10 |
90 |
|
| 1800-2000 |
60 |
12 |
150 |
|
| 2000-2200 |
145 |
29 |
295 |
|
| 2200-2400 |
110 |
22 |
405 |
|
| 2400-2600 |
80 |
16 |
485 |
|
| 2600-2800 |
15 |
3 |
500 |
|
| Разом |
500 |
100 |
||
На рис. 3.2 представлена кумулята розподілу працівників підприємства за розміром заробітної плати.
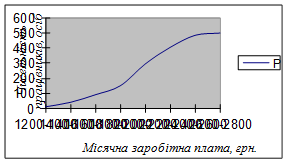
Рис. 3.2 Кумулята розподілу працівників сільськогосподарського підприємства за розміром заробітної плати
3.3 Криві розподіли та їх види
Легко помітити, що розмір прямокутників гістограмми залежить від розміру взятих інтервалів: чим вужче інтервал, тим вужче прямокутник гістограмми й тим ближче східчаста лінія гістограмми до деякої кривої, що виражає закономірність розподілу. Таким чином, залежність частот, або, точніше, щільностей розподілу від розміру варіантів в ідеальному випадку може бути представлена у вигляді деякої функції, зображуваною графічно кривою певного виду. Схематично ж будь-який реальний розподіл можна також зобразити у вигляді деякої кривої, що відтворює основні особливості даного розподілу.
Залежно від виду кривих, що зображують розподіл, можна виділити декілька основних типів розподілів.
Насамперед розподіли по виду їхнього графічного зображення можна розділити на одновершинні й багатовершинні. До одновершинним відносяться ті, у яких один центральний варіант має найбільшу частоту (точніше – найбільшу щільність розподілу), частоти ж варіантів менших і більших, ніж центральний, убувають по мірі видалення розміру варіанта від центрального. При цьому можливо, що частоти убувають однаково і праворуч і ліворуч від центрального значення (рівні між собою). Такі розподіли називаються симетричними.
Якщо частоти убувають ліворуч і праворуч від центру розподілу з різною швидкістю, то такі розподіли називають асиметричними, виділяючи при цьому розподіли, розтягнуті вправо й уліво.
Ступінь асиметрії може бути різною: від зовсім незначної до крайньої, при якій найбільша частота належить до одного із крайніх значень варіантів - найбільшому або, навпаки, найменшому. На рис.3.3 схематично представлені різноманітні види одновершинних розподілів.
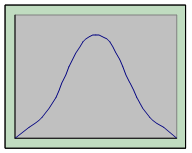
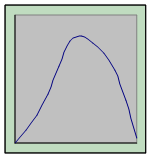
1) Симетричний розподіл 2) Помірно асиметричний 3) Вкрай асиметричний розподіл розподіл
Рис. 3.3
Ідеальний симетричний розподіл украй рідко зустрічається на практиці. Досить близькі йому розподіли чоловіків і жінок по вазі або зросту (при досить великій кількості людей, включених у сукупність).
Основна маса розподілів, із якими доводиться мати справу економісту, це асиметричні розподіли з різним ступенем асиметрії.
Багатовершинні розподіли – це такі розподіли, у яких кілька центрів, інакше, такі, у яких декілька максимумів частот. Багатовершинність розподілу часто є свідченням того, що сукупність складається з неоднорідних, з погляду досліджуваної ознаки, одиниць. Тому, переконавшись у тому, що розподіл має більш ніж один максимум частоти, дослідник повинен ретельно перевірити, чи можна вважати однорідними одиниці, що складають сукупність, або треба для вивчення розбити сукупність на дві або більше однорідні групи[ 4,49].
4. Практичне завдання
Задача 4
Динаміка середньоспискової чисельності робітників підприємства характеризується наступними даними:
Таблиця 4.1
| Рік |
1993 |
1994 |
1995 |
1996 |
1997 |
| Кількість робітників, осіб. |
4850 |
4880 |
4880 |
4900 |
4924 |
З метою аналізу динаміки чисельності робітників підприємства визначте: а) абсолютні прирости, темпи зростання та приросту по роках і до 1993 р., а також абсолютне значення одного відсотку приросту. Здобуті показники представити в таблиці; б) середньорічну чисельність робітників; в) середньорічний абсолютний приріст та середньорічний темп зростання і приросту. Зобразити графічно динаміку чисельності робітників та зробіть висновки.
Розв’язання.
Абсолютний приріст (
) – це різниця між двома рівнями ряду. Він буває ланцюговим (
) і базисним (
) і показує, на скільки одиниць в абсолютному виразі рівень одного періоду більше або менше попереднього рівня.
Темп зростання – це відношення двох рівнів ряду, виражене у відсотках. Він також буває ланцюговим (
) і базисним (
) і показує, у скільки разів рівень даного періоду більше або менше базисного рівня. Якщо з темпу зростання відняти 100%, одержимо темп приросту (
). Абсолютний зміст 1% приросту (А) відповідає сотій частині попереднього рівня, тобто 
.
Розраховані показники заносимо в таблицю 4.2.
Таблиця 4.2
| Рік |
Чисельність робітників, осіб |
Абсолютний приріст, осіб |
Темп зростання, % |
Темп приросту, % |
Абсолютне значення 1% приросту, осіб. |
|||
| Ланцю говий |
Базис ний |
Ланцю говий |
Базис ний |
Ланцюговий |
Базисний |
|||
| 1993 |
4850 |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
| 1994 |
4880 |
30 |
30 |
100.62 |
100.62 |
0.62 |
0,62 |
48.5 |
| 1995 |
4880 |
0 |
30 |
100.00 |
100.62 |
0.00 |
0,62 |
48.8 |
| 1996 |
4900 |
20 |
50 |
100.41 |
101.03 |
0.41 |
1.03 |
48.8 |
| 1997 |
4924 |
24 |
74 |
100.49 |
101.53 |
0,49 |
1.53 |
49 |
Даний динамічний ряд є інтервальним. Інтервал дорівнює 1 року.
Середньорічна чисельність робітників становить
=(4850+4880+4880+4900+4924)/5=4886,8 осіб.
Середньорічний абсолютний приріст визначаємо по формулі:
=(4924-4850)/(5-1)=18,5 осіб.
Середньорічний темп зростання розраховується як середня геометрична з ланцюгових темпів зростання по формулі:
=
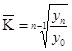=1,0038*100%=100,38%
Середньорічний темп приросту:
=100,38-100=0,38%
Для наочності динаміки середньоспискової чисельності працівників підприємства відобразимо її графічно:
Рис. 4.1 Динаміка середньоспискової чисельності працівників підприємства
Висновок: Як показує аналіз отриманих показників і графік, середньоспискова чисельність працівників підприємства на протязі 5 років щорічно збільшувалася (за винятком 1995 року) і в цілому за 5 років зросла на 74 особи або на 1,53%. В середньому на підприємстві працювало 4887 особи. Середнє зростання чисельності працівників склало 100,38%.
Задача 5
Виробництво молока у районі в першому півріччі характеризується наступними показниками:
Таблиця 4.3
| Дата |
01.01 |
01.02 |
01.03 |
01.04 |
01.05 |
01.06 |
01.07 |
| Виробництво молока, тис. т |
1264 |
1288 |
1325 |
1369 |
1390 |
1450 |
1500 |
Визначте середньомісячне виробництво молока у районі:
а) за перший квартал; б) за другий квартал; в) за перше півріччя.
Обґрунтуйте методи розрахунку середніх рівнів рядів динаміки в задачах 4 і 5.
Розв’язання.
У даному завданні маємо моментальний ряд динаміки, тому що виробництво молока, наведене в таблиці 4.3, не за якийсь період, а в конкретний час (момент). Цей ряд з равностоящими проміжками часу, тому среднесписочное виробництво молока в районі будемо визначати по формулі середньої хронологічної, тому що середня хронологічна використається в тих випадках, коли потрібно розрахувати середню величину за певний відрізок часу. Середню хронологічну визначаємо:
,
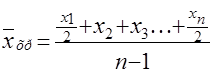де x – рівні ряду;
n – кількість рівнів.
а) середньомісячне виробництво молока за перший квартал
б) середньомісячне виробництво молока за другий квартал
в) середньомісячне виробництво молока за перше півріччя
Таким чином, середньомісячне виробництво молока в районі зростає протягом першого півріччя.
Задача 6
Динаміка середніх цін і обсягу продаж овочів на ринку характеризується наступними даними:
Таблиця 4.4
| Овочі |
Продано, кг |
Середня ціна за 1 кг, грн. |
||
| базисний період |
поточний період |
базисний період |
поточний період |
|
| Огірки |
1800 |
2000 |
1,2 |
1,3 |
| Помідори |
1500 |
1600 |
1,6 |
1,9 |
Визначте: а) індивідуальні індекси цін і фізичного обсягу продаж; б) загальні індекси цін і фізичного обсягу продаж; в) загальний індекс товарообігу; г) як змінився в абсолютному виразі товарообіг поточного періоду в порівнянні з базисним. Зробіть висновки.
Розв’язання.
Індивідуальний індекс ціни характеризує зміни ціни одиниці товару у звітному періоді в порівнянні з базисним і визначається по формулі:
,
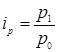де р1 – ціна одиниці продукції у звітному періоді;
р0 – ціна одиниці продукції в базисному періоді.
На огірки: На помідори:
=1,3/1,2=1,08 або 108% =1,9/1,6=1,19 або 119%
Індивідуальний індекс кількості показує, як кількість зробленої або реалізованої продукції в аналізованому періоді змінилася в порівнянні з базисним і визначаємо його по формулі:
,
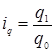де q1 – кількість продукції відповідно у звітному періоді;
q0 – кількість продукції в базисному періоді.
Визначимо індивідуальний індекс фізичного обсягу продажів овочів:
На огірки: На помідори:
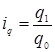=2000/1800=1,11 або 111% 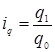=1600/1500=1,06 або 106%
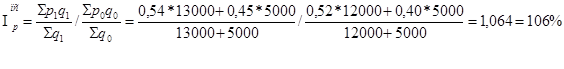
Загальні індекси цін показують, як у середньому ціна на всю зроблену або реалізовану продукцію у звітному році змінилася в порівнянні з базисним періодом.
Загальні індекси цін визначаються по формулі:
,
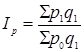де 
- кількість реалізованого товару у звітному періоді за цінами звітного періоду;
- кількість проданого товару у звітному періоді за цінами базисного періоду.
Загальні індекси кількості показують, як у середньому змінилася кількість реалізованої продукції у звітному періоді в порівнянні з базисним періодом.
Загальні індекси кількості визначаються по формулі:
,
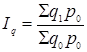де - кількість реалізованого товару у звітному періоді за цінами базисного періоду;
- кількість проданого товару в базисному періоді за цінами базисного періоду.
Загальний індекс товарообігу показує, як обсяг товарообігу у звітному періоді змінився в порівнянні з базисним періодом.
Загальний індекс товарообігу визначаємо по формулі:
,
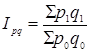де 
- кількість реалізованого товару у звітному періоді за цінами звітного періоду;
- кількість проданого товару в базисному періоді за цінами базисного періоду.
Для того, щоб знайти зміни в абсолютному виразі товарообігу поточного періоду в порівнянні з базисним, потрібно у формулі загального індексу товарообігу із чисельника відняти знаменник.
Тоді одержимо: 5640-4560=1080 грн.
На 1080 грн. Товарообіг в абсолютному вираженні змінився в порівнянні з базисним.
Задача 7
Є наступні дані про зміну товарообігу магазину спортивних товарів:
Таблиця 4.5
| Товар |
Продано товарів у фактичних цінах, тис. грн. |
Зміна кількості проданих товарів у поточному періоді в порівнянні з базисним, % |
|
| базисний період |
поточний період |
||
| Футболки |
1,8 |
2,0 |
Без змін |
| Штани спортивні |
2,4 |
2,5 |
-2 |
| Кросівки |
3,6 |
4,2 |
+3 |
Визначте: а) загальний індекс товарообігу у фактичних цінах; б) загальний індекс товарообігу фізичного обсягу товарообігу; в) загальний індекс цін, використовуючи взаємозвязок індексів. Проаналізуйте отримані результати й зробіть висновки.
Розв’язання.
Вартість товарообігу являє собою добуток ціни товару на кількість проданих товарів. Індекс вартості товарообігу в цьому звязку являє собою добуток індексу цін на індекс кількості, тобто ці індекси взаємозалежні – сполучені.
Загальний індекс товарообігу у фактичних цінах:
=
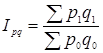1.16 або 116%
На 16% вартість товарообігу у фактичних цінах змінилася в поточному періоді в порівнянні з базисним.
Загальний індекс фізичного обсягу товарообігу знайдемо по наступній формулі:
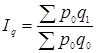
- це значення відомо й дорівнює 7,8.
У чисельнику відомо q1. Відома також зміна кількості проданих товарів у звітному періоді в порівнянні з базисним, що дає можливість визначити індивідуальні індекси кількостей, за допомогою якої знаходим загальний індекс фізичного обсягу товарообігу:
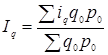
Обчислюємо iq для всіх товарів:
- для футболок iq=1;
- для штанів iq=1-0,02=0,88;
- для кросівок iq=1+0,03=1,03;
1,008 або 100,8%
Між загальними індексами існує взаємозвязок: добуток загального індексу цін на загальний індекс кількості рівняється індексу товарообігу у фактичних цінах:
Отже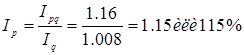 
Аналізуючи отримані результати, можна зробити висновок про те, що збільшення вартості товарообігу в поточному періоді повязане з підвищенням цін на товари, які підвищилися в середньому на 16%, а обсяг продажів виріс у середньому на 0,8%.
Задача 8
Використовуючи дані задачі 1, визначте тісноту звязку між собівартістю одиниці (результативна ознака) і обсягом її виробництва (факторна ознака) за допомогою лінійного коефіцієнта кореляції. Зробіть висновки.
Таблиця 4.6
| Номер підприємства |
Обсяг виробництва, тис. шт. |
Собівартість одиниці продукції, грн. |
Номер підприємства |
Обсяг виробництва, тис. шт. |
Собівартість одиниці продукції, грн. |
| 1 |
10 |
2,8 |
11 |
7 |
3,4 |
| 2 |
6 |
3,8 |
12 |
10 |
3,0 |
| 3 |
12 |
2,6 |
13 |
2 |
4,4 |
| 4 |
3 |
4,2 |
14 |
9 |
2,8 |
| 5 |
7 |
4,0 |
15 |
10 |
2,9 |
| 6 |
4 |
3,3 |
16 |
14 |
2,0 |
| 7 |
8 |
3,3 |
17 |
4 |
4,1 |
| 8 |
5 |
4,0 |
18 |
8 |
3,2 |
| 9 |
17 |
2,4 |
19 |
12 |
3,0 |
| 10 |
11 |
2,8 |
20 |
15 |
2,2 |
Розв’язання.
Лінійний коефіцієнт кореляції (r) являє собою відношення середньоквадратичного відхилення по x(x) до середньоквадратичного відхилення по в(у) і помноженого на коефіцієнт регресії (b). Характеризує тісноту звязку між факторною й результативною ознаками. Лінійний коефіцієнт кореляції може приймати значення від 0±1. Якщо r=0, то звязок відсутній, якщо r=1, то звязок повний і функціональний (але звязок не повинен бути більше 1).
Для розрахунків використаємо наступні формули й отримані дані занесемо в таблицю 4.7.:
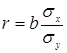, де
;
;
.
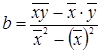Таблиця 4.7 Розрахунок лінійного коефіцієнта кореляції.
| Номер підприємства (n) |
Обсяг виробництва, тис.шт. (x) |
Собівартість одиниці продукції, грн. (y) |
x·y |
X2 |
Y2 |
| 1 |
10 |
2.8 |
28 |
100 |
7.84 |
| 2 |
6 |
3.8 |
22.8 |
36 |
14.44 |
| 3 |
12 |
2.6 |
31.2 |
144 |
6.76 |
| 4 |
3 |
4.2 |
12.6 |
9 |
17.64 |
| 5 |
7 |
4.0 |
28 |
49 |
16 |
| 6 |
4 |
3.3 |
13.2 |
16 |
10.89 |
| 7 |
8 |
3.3 |
26.4 |
64 |
10.89 |
| 8 |
5 |
4.0 |
20 |
25 |
16 |
| 9 |
17 |
2.4 |
40.8 |
289 |
5.76 |
| 10 |
11 |
2.8 |
30.8 |
121 |
7.84 |
| 11 |
7 |
3.4 |
23.8 |
49 |
11.56 |
| 12 |
10 |
3.0 |
30 |
100 |
9 |
| 13 |
2 |
4.4 |
8.8 |
4 |
19.36 |
| 14 |
9 |
2.8 |
25.2 |
81 |
7.84 |
| 15 |
10 |
2.9 |
29 |
100 |
5.41 |
| 16 |
14 |
2.0 |
28 |
196 |
4 |
| 17 |
4 |
4.1 |
16.4 |
16 |
16.81 |
| 18 |
8 |
3.2 |
25.6 |
64 |
10.24 |
| 19 |
12 |
3.0 |
36 |
144 |
9 |
| 20 |
15 |
2.2 |
33 |
225 |
48.4 |
| N=20 |
x=8.7 |
y=3.21 |
x·y=25.48 |
x2=91.6 |
y2=10.756 |
=8.72=75.69; 
=3,212=10,304
=8.7·3.21=27,927
На підставі наведених розрахунків обчислимо інші значення:
=3.21-(-0.154·8.7)=4.55
Лінійний коефіцієнт кореляції дорівнює:
З коефіцієнта кореляції видно, що залежність між змінними зворотна (коефіцієнт кореляції негативний) і звязок між ними сильний (дорівнює 0,913).
Висновок
Статистичний аналіз масових явищ і процесів є необхідною ланкою в системі управління економікою та державою в цілому. Передусім, за допомогою статистики здійснюється “зворотній зв’язок”, тобто потік інформації йде від об’єкта до суб’єкта управління – керівництва підприємств, об’єднань, територіальних, галузевих і центральних органів влади. Без вірогідної, всебічної і своєчасної інформації ефективні управлінські рішення неможливі. Хто володіє інформацією, той володіє світом.
Як суспільна наука статистика не може розвиватись окремо від теоретичних наук про суспільство, зокрема економічної теорії та соціології. Спираючись на суть, якісну природу явищ, через узагальнення масових даних статистика вивчає характер і дію основних законів у реальному житті, проводить прогнозні розрахунки, які конче необхідні при грунтуванні напрямів соціально-економічної політики.
Суспільство в процесі свого розвитку ставить перед статистикою нові завдання, вимагає від неї більш широкого охоплення явищ і прцесів суспільного життя. Це сприяє розвитку статистики і формуванню її галузей.
В даній курсовій роботі був розглянутий такий складовий елемент статистичного зведення, як викладення результатів зведення і групування у вигляді варіаційних рядів розподілу, роль та значення їх в аналізі даних, побудова рядів розподілу одиниць сукупностей за варіюючими ознаками та графічне зображення їх. У ході виконання курсової роботи було зазначено, що ряди розподілу є особливим видом групувань в статистиці. Рядом розподілу називають групування, яке характеризує склад (структуру) явища в даний період часу.
При виконанні курсової роботи були застосовані дані конкретного підприємства, таким чином набуті знання мали своє застосування на конкретних даних одиниць сукупності.
Перелік посилань
1. Теорія статистики, підручник, – третє видання, перероблене та доповнене, О.І. Кулинич, Р.О. Кулинич, Київ ”Знання”, 2006
2. Теорія статистики, навчальний посібник, В.Л. Бек, Київ: ЦУЛ 2002
3. Статистика, підручник, – друге видання, перероблене та доповнене, О.Є.Лугінін, Центр учбової літератури, 2007
4. Общая теория статистики,учебное пособие, – издание второе, переработанное и дополненное, под редакцией А.Я. Боярского, Г.Л. Громыко, Издательство Московского университета, 1985
[ 1,10] Теорія статистики, О. І. Кулинич, Р. О. Кулинич, Київ ”Знання”, 2006
[ 2,20] Теорія статистики, навчальний посібник, В. Л. Бек, ЦУЛ 2002
[ 2,47] Теорія статистики, навчальний посібник, В. Л. Бек, ЦУЛ 2002
[ 2,48] Теорія статистики, навчальний посібник, В. Л. Бек, ЦУЛ 2002
[ 3,55] Статистика, підручник, 2-е видання, перероблене та доповнене, О. Є.Лугінін, Центр учбової літератури, 2007
[ 2,55] Теорія статистики, навчальний посібник, В. Л. Бек, ЦУЛ 2002
[ 2,58] Теорія статистики, навчальний посібник, В. Л. Бек, ЦУЛ 2002
[ 3,62] Статистика,Підручник, 2-е видання, перероблене та доповнене, О. Є.Лугінін, Центр учбової літератури, 2007
[ 3,65] Статистика,Підручник, 2-е видання, перероблене та доповнене, О. Є.Лугінін, Центр учбової літератури, 2007
[ 2,61] Теорія статистики, навчальний посібник, В. Л. Бек, ЦУЛ 2002
[ 4,49] Общая теория статистики, под ред. А. Я. Боярского, Г. Л. Громыко, Изд-во Московского университета, 1985