Исследование смены режимов течения. Определение критических чисел Рейнольдса
СОДЕРЖАНИЕ: Демонстрация режимов течения жидкости и экспериментальное определение критических чисел Рейнольдса для труб круглого сечения. Структура и основные элементы установки Рейнольдса, ее функциональные особенности и назначение, определение параметров.Лабораторная работа №1
Тема: «Исследование смены режимов течения. Определение критических чисел Рейнольдса»
Цель работы
Демонстрация режимов течения жидкости и экспериментальное определение критических чисел Рейнольдса для труб круглого сечения.
Основные сведения
Режим течения определяется соотношением возмущающей течение силы инерции и стабилизирующей течение силы вязкости. Отношение этих сил выражается безразмерным числом Рейнольдса:
![]() ,
,
где u – средняя скорость течения жидкости по сечению трубы;
L – характерный линейный размер поперечного сечения, заполненного жидкостью (так называемого «живого сечения») для труб круглого сечения L=d;
n – кинематическая вязкость.
Средняя скорость находится по формуле
![]() ,
,
где Q – расход потока, т.е. объем жидкости, протекающий за единицу времени через данное сечение потока, площадь которого равна S. Возможны два принципиально отличающихся режима течения жидкости, получивших название ламинарного (слоистого) и турбулентного (бурного, возмущенного) режимов. При достаточно малых скоростях основного потока, когда число Рейнольдса меньше определенного критического (Re Reкр ), инерционная сила незначительна по сравнению с силой вязкости, которая упорядочивает движение жидкости, создавая ламинарное движение. При этом окрашенная струйка, введенная в поток, вытягивается вдоль течения в виде тонко очерченной линии. При Re»Reкр форма окрашенной струйки резко меняется – она приобретает вид более или менее отчетливых завитков. Такая картина отвечает начальной стадии развития турбулентности, а момент ее появления – началу перехода от ламинарного режима к турбулентному (переходный режим). При Re Reкр силы инерции преобладают над силами вязкости, и наступает вполне развитая турбулентность. Критическое число Рейнольдса, как правило, заключено в некоторых пределах: Reкр.н. Reкр Reкр.в , где Reкр.в. – максимальное критическое число Рейнольдса, соответствующее переходу ламинарного режима в турбулентный; Reкр.н – нижнее критическое число Рейнольдса, т.е. минимально возможное число, соответствующее переходу турбулентного режима в ламинарный.
Установление режима движения имеет большое практическое значение, так как он определяет важнейшие характеристики потока, как распределение скоростей, гидравлическое сопротивление, теплоотдачу и др.
Описание установки
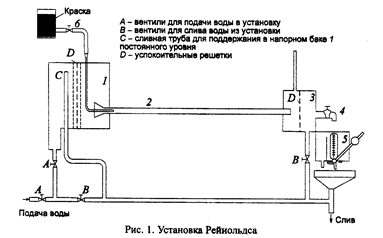
Установка Рейнольдса (рис. 1) состоит из напорного бака 1, прозрачной трубы 2 круглого сечения с плавным входом, промежуточного бака 3 с регулирующим краном 4, расходомерного устройства 5, а также системы подачи и слива рабочей жидкости (воды) и системы подачи краски. Промежуточный бак 3 предназначен для устранения влияния крана 4 на распределение скоростей в трубе 2. Расходомерное устройство 5 представляет собой емкость, в днище которой находятся калибровочные отверстия с насадками. При том или ином расходе, поступающем в емкость из крана 4, жидкость в расходомером устройстве 5 устанавливается на определенном уровне, который отсчитывается по шкале. По полученному уровню Н с помощью экспериментальных (тарировочных) зависимостей вычисляют расход Q . Такие устройства для измерения расхода называются данаидами.
Обработка данных:
течение жидкость рейнолдс труба
Таблица 1
| № опытов | Температура t, С | Кинематическая вязкость , см2 /с | Уровень в мерном бачке Н, мм | Расход Q, см3 /с | Средняя скорость
|
Число Рейнольдса
|
Режим по визуальным наблюдениям |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 20 | 0,01007 | 25 | 13,489 | 4,766 | 899 | Л |
| 2 | 20 | 0,01007 | 205 | 36,307 | 12,829 | 2435 | ЛТ |
| 3 | 20 | 0,01007 | 260 | 39,810 | 14,067 | 2654 | Т |
| 4 | 20 | 0,01007 | 170 | 33,113 | 11,700 | 2207 | ТЛ |
Внутренний диаметр d = 1,9 см.
1. Кинематическая вязкость в зависимости от температуры находится по эмпирической формуле Пуазеля:
![]()
![]() .
.
2. По известному уровню Н (мм) с помощью эмпирической зависимости (для малого калибровочного отверстия
3. Средняя скорость движения воды в трубе находится по формуле:
![]() ,
,
где S – площадь поперечного сечения трубы ![]() .
.
4. Число Рейнольдса для трубы находится по формуле: ![]() .
.
5. Среднее число Рейнольдса находится как
![]()