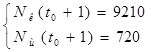Качественное исследование модели хищник-жертва
СОДЕРЖАНИЕ: Математическое моделирование динамики биологических видов (популяций) Т. Мальтусом. Параметры и основное уравнение модели хищник-жертва, ее практическое применение. Качественное исследование элементарной и обобщенной модификаций модели В. Вольтерра.Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Ижевский государственный технический университет»
Факультет «Прикладная математика»
Кафедра «Математическое моделирование процессов и технологий»
Курсовая работа
по дисциплине «Дифференциальные уравнения»
Тема: «Качественное исследование модели хищник-жертва»
Ижевск 2010
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ
1. ПАРАМЕТРЫ И ОСНОВНОЕ УРАВНЕНИЕ МОДЕЛИ «ХИЩНИК-ЖЕРТВА»
2. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ ЭЛЕМЕНТАРНОЙ МОДЕЛИ «ХИЩНИК-ЖЕРТВА»
2.1 Модель трофического взаимодействия по типу «хищник—жертва»
2.2 Обобщенные модели Вольтера типа «хищник-жертва».
3. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ МОДЕЛИ «ХИЩНИК-ЖЕРТВА»
ЗАКЛЮЧЕНИЕ
СПИСОК ЛИТЕРАТУРЫ
ВВЕДЕНИЕ
В настоящее время задачи экологии имеют первостепенное значение. Важным этапом решения этих задач является разработка математических моделей экологических систем.
Одной из основных задач экологии па современном этапе является изучение структуры и функционирования природных систем, поиск общих закономерностей. Большое влияние на экологию оказала математика, способствующая становлению математической экологии, особенно такие её разделы, как теория дифференциальных уравнений, теория устойчивости и теория оптимального управления.
Одной из первых работ в области математической экологии была работа А.Д. Лотки (1880 - 1949), который первый описал взаимодействие различных популяций, связанных отношениями хищник - жертва. Большой вклад в исследование модели хищник -жертва внесли В. Вольтерра (1860 - 1940), В.А. Костицин (1883-1963) В настоящее время уравнения описывающие взаимодействие популяций, называются уравнениями Лотки — Вольтерра.
Уравнения Лотки - Вольтерра описывают динамику средних величин - численности популяции. В настоящее время на их основе построены более общие модели взаимодействия популяций, описываемые интегро-дифференциальными уравнениями, исследуются управляемые модели хищник - жертва.
Одной из важных проблем математической экологии является проблема устойчивости экосистем, управления этими системами. Управление может осуществляться с целью перевода системы из одного устойчивого состояния в другое, с целью её использования или восстановления.
1. ПАРАМЕТРЫ И ОСНОВНОЕ УРАВНЕНИЕ МОДЕЛИ ХИЩНИК-ЖЕРТВА
Попытки математического моделирования динамики как отдельных биологических популяций, так и сообществ, включающих взаимодействующие популяции различных видов, предпринимались давно. Одна из первых моделей роста изолированной популяции (2.1) была предложена еще в 1798 г. Томасом Мальтусом:
, (1.1)
Данная модель задается следующими параметрами:
N — численность популяции;
— разность между коэффициентами рождаемости и смертности.
Интегрируя это уравнение получаем:
, (1.2)
где N(0) – численность популяции в момент t = 0. Очевидно, что модель Мальтуса при 0 дает бесконечный рост численности, что никогда не наблюдается в природных популяциях, где ресурсы, обеспечивающие этот рост, всегда ограничены. Изменения численности популяций растительного и животного мира нельзя описывать простым законом Мальтуса, на динамику роста влияют многие взаимосвязанные причины – в частности, размножение каждого вида саморегулируется и видоизменяется так, чтобы этот вид сохранялся в процессе эволюции. [1]
Математическим описанием этих закономерностей занимается математическая экология – наука об отношениях растительных и животных организмов и образуемых ими сообществ между собой и с окружающей средой.
Наиболее серьезное исследование моделей биологических сообществ, включающих в себя несколько популяций различных видов, было проведено итальянским математиком Вито Вольтерра:
,
где 
— численность популяции;
— коэффициенты естественного прироста (или смертности) популяции; 
— коэффициенты межвидового взаимодействия. В зависимости от выбора коэффициентов модель описывает либо борьбу видов за общий ресурс, либо взаимодействие типа хищник — жертва, когда один вид является пищей для другого. Если в работах других авторов основное внимание уделялось построению различных моделей, то В. Вольтерра провел глубокое исследование построенных моделей биологических сообществ. Именно с книги В. Вольтерра, по мнению многих ученых, началась современная математическая экология.
2. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ ЭЛЕМЕНТАРНОЙ МОДЕЛИ «ХИЩНИК-ЖЕРТВА»
2.1 Модель трофического взаимодействия по типу «хищник—жертва»
Рассмотрим модель трофического взаимодействия по типу «хищник—жертва», построенную В. Вольтерром. Пусть имеется система, состоящая из двух видов, из которых один поедает другой.
Рассмотрим случай, когда один из видов является хищником, а другой — жертвой, и будем считать, что хищник питается только жертвой. Примем следующую простую гипотезу:
— коэффициент прироста жертвы;
— коэффициент прироста хищника;
— численность популяции жертвы;
— численность популяции хищника;
— коэффициент естественного прироста жертвы;
— скорость потребления жертвы хищником;
— коэффициент смертности хищника в отсутствие жертвы;
— коэффициент «переработки» хищником биомассы жертвы в собственную биомассу.
Тогда динамика численности популяций в системе хищник — жертва будет описываться системой дифференциальных уравнений (2.1):
(2.1)
где все коэффициенты положительные и постоянные.
Модель имеет равновесное решение (2.2):
(2.2)
По модели (2.1) доля хищников в общей массе животных выражается формулой 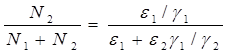(2.3):
(2.3)
Анализ устойчивости состояния равновесия по отношению к малым возмущениям показал, что особая точка (2.2) является «нейтрально» устойчивой (типа «центр»), т. е. любые отклонения от равновесия не затухают, но переводят систему в колебательный режим с амплитудой, зависящей от величины возмущения. Траектории системы на фазовой плоскости 
имеют вид замкнутых кривых, расположенных на различных расстояниях от точки равновесия (рис. 1).
Рис. 1 – Фазовый «портрет» классической вольтерровой системы «хищник-жертва»
Разделив первое уравнение системы (2.1) на второе, получим дифференциальное уравнение (2.4) для кривой на фазовой плоскости .
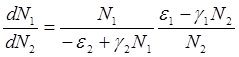(2.4)
Интегрируя данное уравнение получим:
(2.5)
где 
- постоянная интегрирования, где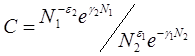 
Несложно показать, что движение точки по фазовой плоскости будет происходить только в одну сторону. Для этого удобно сделать замену функций и 
, перенеся начало координат на плоскости в стационарную точку (2.2) и введя затем полярные координаты:
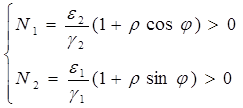(2.6)
В таком случае, подставив значения системы (2.6) в систему (2.1), будем иметь:
(2.7)
Умножив первое уравнение на 
, а второе — на 
и сложив их, получим:
(2.8)
После аналогичных алгебраических преобразований получим уравнение для 
:
(2.9)
Величина 
, как видно из (4.9), всегда больше нуля. Таким образом, не меняет знака, и вращение все время идет в одну сторону.
Интегрируя (2.9) найдем период:
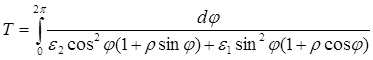(2.10)
Когда мало, то уравнения (2.8) и (2.9) переходят в уравнения эллипса. Период обращения в этом случае равен:
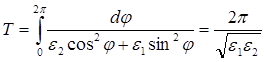(2.11)
Исходя из периодичности решений уравнений (2.1), можно получить некоторые следствия. Представим для этого (2.1) в виде:
(2.12)
и проинтегрируем по периоду:
(2.13)
Так как подстановки от 
и 
в силу периодичности обращаются в нуль, средние по периоду оказываются равными стационарным состояниям (2.14):
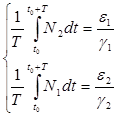(2.14)
Простейшие уравнения модели «хищник—жертва» (2.1) обладают рядом существенных недостатков. Так, в них предполагается неограниченность пищевых ресурсов для жертвы и неограниченный рост хищника, что противоречит экспериментальным данным. Кроме того, как видно из рис. 1, ни одна из фазовых кривых не выделена с точки зрения устойчивости. При наличии даже небольших возмущающих воздействий траектория системы будет все дальше уходить от положения равновесия, амплитуда колебаний расти, и система достаточно быстро разрушится.
Несмотря на недостатки модели (2.1), представления о принципиально колебательном характере динамики системы «хищник— жертва» получили широкое распространение в экологии. Взаимодействиями «хищник—жертва» объясняли такие явления, как колебания численности хищных и мирных животных в промысловых зонах, колебания в популяциях рыб, насекомых и т. д. На самом деле колебания численности могут быть обусловлены и другими причинами.
Предположим, что в системе хищник — жертва происходит искусственное уничтожение особей обоих видов, и рассмотрим вопрос о том, каким образом уничтожение особей влияет на средние значения их численности, если осуществляется пропорционально этой численности с коэффициентами пропорциональности 
и 
соответственно для жертвы и хищника. С учетом сделанных предположений систему уравнений (2.1) перепишем в виде:
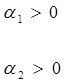(2.15)
Предположим, что 
, т. е. коэффициент истребления жертвы меньше коэффициента ее естественного прироста. В этом случае также будут наблюдаться периодические колебания численности. Вычислим средние значения численностей:
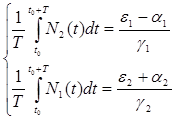(2.16)
Таким образом, если , то средняя численность популяций жертвы возрастает, а хищника — убывает.
Рассмотрим случай, когда коэффициент истребления жертвы больше коэффициента ее естественного прироста, т. Е 
. В этом случае 
при любых 
, и, следовательно, решение первого уравнения (2.15) ограничено сверху экспоненциально убывающей функцией 
, т. е. 
при 
.
Начиная с некоторого момента времени t, при котором 
, решение второго уравнения (2.15) также начинает убывать и при стремится к нулю. Таким образом, в случае оба вида исчезают.
2.1 Обобщенные модели Вольтера типа «хищник-жертва»
Первые модели В. Вольтерра, естественно, не могли отражать все стороны взаимодействия в системе хищник — жертва, поскольку они были в значительной мере упрощены относительно реальных условий. Например, если численность хищника равна нулю, то из уравнений (1.4) следует, что численность жертвы неограниченно возрастает, что не соответствует действительности. Однако ценность этих моделей состоит именно в том, что они были основой, на которой быстрыми темпами начала развиваться математическая экология.
Появилось большое число исследований различных модификаций системы хищник — жертва, где были построены более общие модели, учитывающие в той или иной степени реальную ситуацию в природе.
В 1936 г. А.Н. Колмогоров предложил использовать для описания динамики системы хищник — жертва следующую систему уравнении:
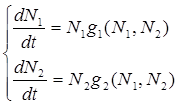
, (2.17)
где 
убывает с возрастанием численности хищников, а 
возрастает с увеличением численности жертвы.
Эта система дифференциальных уравнений в силу ее достаточной общности позволяет хорошо учитывать реальное поведение популяций и вместе с тем проводить качественный анализ ее решений.
Позднее в своей работе, Колмогоров исследовал подробно менее общую модель:
(2.18)
Различные частные случаи системы дифференциальных уравнений (2.18) исследовались многими авторами. В таблице приведены различные частные случаи функций 
, 
, 
.
Таблица 1 - Различные модели сообщества «хищник-жертва»
|
|
|
Авторы |
|
 |
 |
Вольтерра-Лотка |
 |
|
 |
Гаузе |
|
|
 |
Пислоу |
|
 |
|
Холинг |
|
 |
|
Ивлев |
|
 |
|
Рояма |
 |
 |
 |
Шимазу |
|
 |
 |
Мэй |
математическое моделирование хищник жертва
3. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ МОДЕЛИ ХИЩНИК-ЖЕРТВА
Рассмотрим математическую модель совместного существования двух биологических видов (популяций) типа хищник - жертва, называемую моделью Вольтерра - Лотки.
Пусть два биологических вида совместно обитают в изолированной среде. Среда стационарна и обеспечивает в неограниченном количестве всем необходимым для жизни один из видов, который будем называть жертвой. Другой вид - хищник также находится в стационарных условиях, но питается лишь особями первого вида. Это могут быть караси и щуки, зайцы и волки, мыши и лисы, микробы и антитела и т. д. Будем для определенности называть их карасями и щуками.
Заданы следующие начальные показатели:
| Наименование показателя | Щуки | Караси |
 — начальная численность популяции |
10000 | 800 |
 —коэффициент естественного прироста/смертности |
1,1 |
0,001 |
 —коэффициенты межвидового взаимодействия |
0,0001 |
0,0001 |
Со временем число карасей и щук меняется, но так как рыбы в пруду много, то не будем различать 1020 карасей или 1021 и поэтому будем считать 
и 
непрерывными функциями времени t. Будем называть пару чисел (
,) состоянием модели.
Очевидно, что характер изменения состояния (,) определяется значениями параметров. Изменяя параметры и решая систему уравнений модели, можно исследовать закономерности изменения состояния экологической системы во времени.
В экосистеме скорость изменения численности каждого вида также будем считать пропорциональной его численности, но только с коэффициентом, который зависит от численности особей другого вида. Так, для карасей этот коэффициент уменьшается с увеличением числа щук, а для щук увеличивается с увеличением числа карасей. Будем считать эту зависимость также линейной. Тогда получим систему из двух дифференциальных уравнений:
Эта система уравнений и называется моделью Вольтерра-Лотки. Числовые коэффициенты 
, 
, 
- называются параметрами модели. Очевидно, что характер изменения состояния (,) определяется значениями параметров. Изменяя эти параметры и решая систему уравнений модели, можно исследовать закономерности изменения состояния экологической системы.
Проинтегрируем оба уравнения систему по t, которое будет изменяться от 
- начального момента времени, до 
, где T – период, за который происходят изменения в экосистеме. Пусть в нашем случае период равен 1 году. Тогда система принимает следующий вид:
;
;
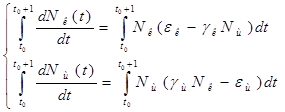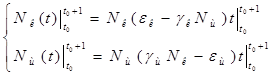Принимая =
и =
приведем подобные слагаемые, получим систему, состоящую из двух уравнений:
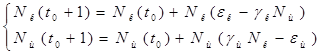
Подставив в полученную систему исходные данные получим популяцию щук и карасей в озере спустя год:
