Кратные интегралы

СОДЕРЖАНИЕ: Министерство образования и науки Российской Федерации Курсовая работа По дисциплине: Высшая математика (Основы линейного программирования) На тему: КРАТНЫЕ ИНТЕГРАЛЫ

Министерство образования и науки Российской Федерации

Курсовая работа

По дисциплине: Высшая математика

(Основы линейного программирования)

На тему: КРАТНЫЕ ИНТЕГРАЛЫ

Выполнил: ______________

Преподаватель:___________

Дата ___________________

Оценка _________________

Подпись ________________

ВОРОНЕЖ 2008

Содержание

1 Кратные интегралы

1.1 Двойной интеграл

1.2 Тройной интеграл

1.3 Кратные интегралы в криволинейных координатах

1.4 Геометрические и физические приложения кратных интегралов

2 Криволинейные и поверхностные интегралы

2.1 Криволинейные интегралы

2.2 Поверхностные интегралы

2.3 Геометрические и физические приложения

Список используемой литературы

1 Кратные интегралы

1.1 Двойной интеграл

Рассмотрим в плоскости Оху замкнутую область D, ограниченную линией L. Разобьем эту область какими-нибудь линиями на п частей , а соответствующие наибольшие расстояния между точками в каждой из этих частей обозначим d₁ , d₂ , ..., d_n . Выберем в каждой части точку Р_i .

Пусть в области D задана функция z = f(x, y). Обозначим через f(P₁ ), f(P₂ ),…, f(P_n ) значения этой функции в выбранных точках и составим сумму произведений вида f(P_i )S_i :

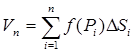, (1)

называемую интегральной суммой для функции f(x, y) в области D.

Если существует один и тот же предел интегральных сумм (1) при и , не зависящий ни от способа разбиения области D на части, ни от выбора точек P_i в них, то он называется двойным интегралом от функции f(x, y) по области D и обозначается

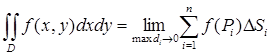. (2)

Вычисление двойного интеграла по области D, ограниченной линиями x = a, x = b( a b ), где ₁ (х) и ₂ (х) непрерывны на [a, b] (рис. 1) сводится к последовательному вычислению двух определенных интегралов, или так называемого двукратного интеграла:

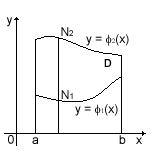
Рис. 1

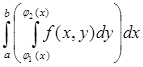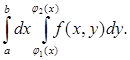= (3)

1.2 Тройной интеграл

Понятие тройного интеграла вводится по аналогии с двойным интегралом.

Пусть в пространстве задана некоторая область V, ограниченная замкнутой поверхностью S. Зададим в этой замкнутой области непрерывную функцию f(x, y, z). Затем разобьем область V на произвольные части v_i , считая объем каждой части равным v_i , и составим интегральную сумму вида

, (4)

Предел при интегральных сумм (11), не зависящий от способа разбиения области V и выбора точек P_i в каждой подобласти этой области, называется тройным интегралом от функции f(x, y, z) по области V:

. (5)

Тройной интеграл от функции f(x,y,z) по области V равен трехкратному интегралу по той же области:

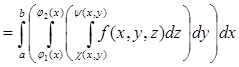. (6)

1.3 Кратные интегралы в криволинейных координатах

Введем на плоскости криволинейные координаты, называемые полярными. Выберем точку О (полюс) и выходящий из нее луч (полярную ось).

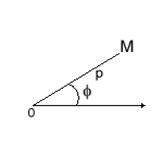
Рис. 2 Рис. 3

Координатами точки М (рис. 2) будут длина отрезка МО – полярный радиус и угол между МО и полярной осью: М(,). Отметим, что для всех точек плоскости, кроме полюса, 0, а полярный угол будем считать положительным при измерении его в направлении против часовой стрелки и отрицательным – при измерении в противоположном направлении.

Связь между полярными и декартовыми координатами точки М можно задать, если совместить начало декартовой системы координат с полюсом, а положительную полуось Ох – с полярной осью (рис. 3). Тогда x=cos, у=sin . Отсюда , tg.

Зададим в области D, ограниченной кривыми =₁ () и =₂ (), где _{1 2} , непрерывную функцию z = f(, ) (рис. 4).

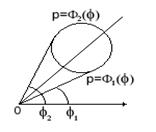
Рис. 4

Тогда

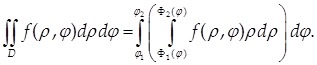(7)

В трехмерном пространстве вводятся цилиндрические и сферические координаты.

Цилиндрические координаты точки Р(,,z) – это полярные координаты , проекции этой точки на плоскость Оху и аппликата данной точки z (рис.5).

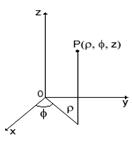
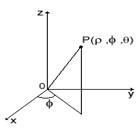
Рис.5 Рис.6

Формулы перехода от цилиндрических координат к декартовым можно задать следующим образом:

x = cos, y = sin, z = z. (8)

В сферических координатах положение точки в пространстве определяется линейной координатой r – расстоянием от точки до начала декартовой системы координат (или полюса сферической системы), – полярным углом между положительной полуосью Ох и проекцией точки на плоскость Оху, и – углом между положительной полуосью оси Оz и отрезком OP (рис.6). При этом

Зададим формулы перехода от сферических координат к декартовым:

x = rsincos, y = rsinsin, z = rcos. (9)

Тогда формулы перехода к цилиндрическим или сферическим координатам в тройном интеграле будут выглядеть так:

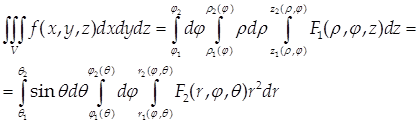, (10)

где F₁ и F₂ – функции, полученные при подстановке в функцию fвместо x, y, z их выражений через цилиндрические (8) или сферические (9) координаты.

1.4 Геометрические и физические приложения кратных интегралов

1) Площадь плоской области S: (11)

Пример 1.

Найти площадь фигуры D, ограниченной линиями

у = 2, у = 5.

Решение.

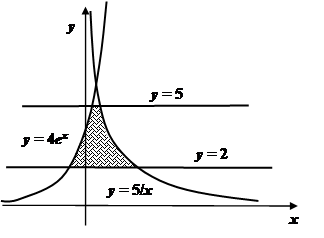
Эту площадь удобно вычислять, считая у внешней переменной. Тогда границы области задаются уравнениями и

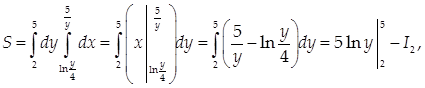
где 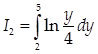вычисляется с помощью интегрирования по частям:

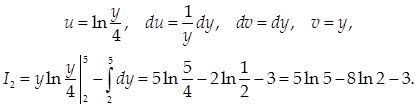
Следовательно,

2) Объем цилиндроида, то есть тела, ограниченного частью поверхности S:z = f(x,y) , ограниченной контуром L, проекцией D этой поверхности на плоскость Оху и отрезками, параллельными оси Оz и соединяющими каждую точку контура L с соответствующей точкой плоскости Оху:

(12)

3) Площадь части криволинейной поверхности S, заданной уравнением z = f(x,y), ограниченной контуром L:

(13)

где D – проекция S на плоскость Оху.

4) Момент инерции относительно начала координат О материальной плоской фигуры D:

(14)

Пример 2.

Найти момент инерции однородной круглой пластинки

(x – a)² + (y – b)² 4b² относительно начала координат.

Решение.

В силу однородности пластинки положим ее плотность (х,у) = 1.

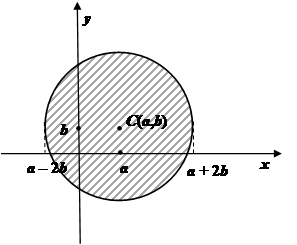
Центр круга расположен в точке C(a, b), а его радиус равен 2b.

Уравнения границ пластинки имеют вид

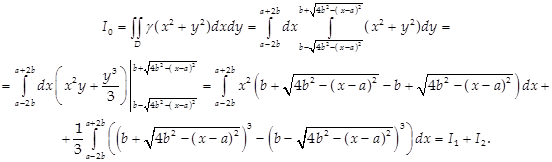
Вычислим каждый из полученных интегралов отдельно.

Для вычисления интеграла I₁ сделаем замену:

при x = a – 2b при x = a + 2b

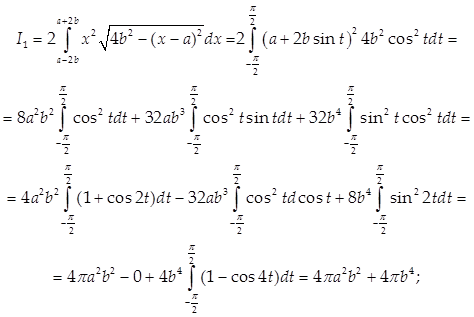
Для вычисления интеграла I₂ преобразуем подынтегральную функцию по формуле разности кубов:

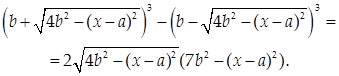
Тогда

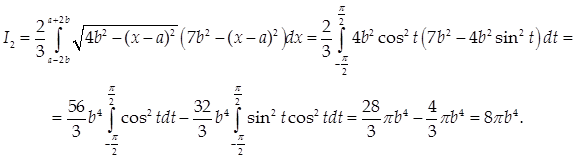
Следовательно,

Моменты инерции фигуры D относительно осей Ох и Оу:

(15)

5) Масса плоской фигуры D переменной поверхностной плотности = (х, у):

(16)

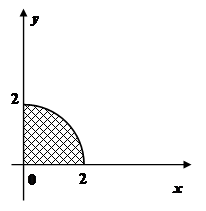
Пример 3.

Найти массу пластинки D плотности = ух³ , если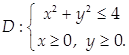

Решение.

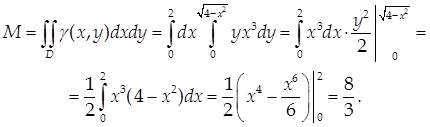
Координаты центра масс плоской фигуры переменной поверхностной плотности = (х, у):

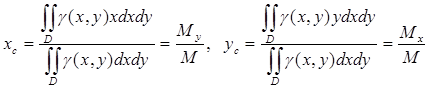(17)

Пример 4.

Найти центр тяжести однородной пластины D, ограниченной кривыми у² = ах и

Решение.

Так как пластина однородна, т.е. ее плотность постоянна, то можно принять ее за единицу.

Тогда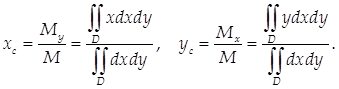

Найдем массу пластины, а для этого определим абсциссу точки пересечения ограничивающих ее линий:

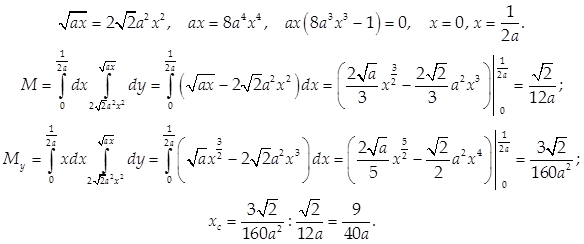
Соответственно

6) Объем тела V:

(18)

Пример 5.

Найти объем тела V, ограниченного поверхностями

Решение.

Найдем проекцию тела на плоскость Оху (при этом заметим, что плоскость проектируется на эту плоскость в виде прямой х = 0):

Определим абсциссу точки пересечения кривых у = х² и х + у = 2:

посторонний корень. Тогда, используя формулу (18), получаем:

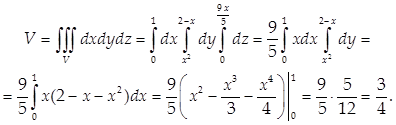
7) Масса тела V плотности = (x, y, z):

(19)

8) Моменты инерции тела V относительно координатных осей и начала координат:

(20)

(21)

где (х, y, z) – плотность вещества.

Статические моменты тела относительно координатных плоскостей Oyz, Oxz, Oxy:

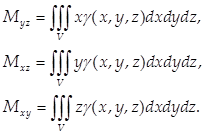(22)

9) Координаты центра масс тела:

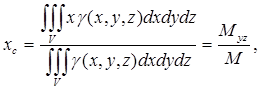
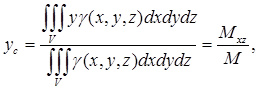
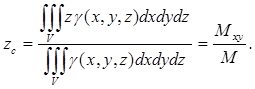
II . Криволинейные и поверхностные интегралы

2.1 Криволинейные интегралы

Рассмотрим на плоскости или в пространстве кривую L и функцию f, определенную в каждой точке этой кривой. Разобьем кривую на части s_i длиной s_i и выберем на каждой из частей точку M_i . Назовем d длину наибольшего отрезка кривой: .

Криволинейным интегралом первого рода от функции f по кривой L называется предел интегральной суммы , не зависящий ни от способа разбиения кривой на отрезки, ни от выбора точек M_i :

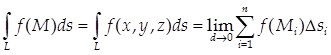(24)

Если кривую L можно задать параметрически:

x = (t), y = (t), z = (t), t₀ t T,

то способ вычисления криволинейного интеграла первого рода задается формулой

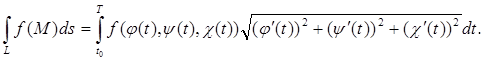(25)

В частности, если кривая L задана на плоскости явным образом:

у=(х), где х₁ х х₂ , формула (40) преобразуется к виду:

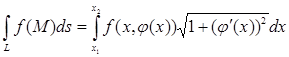. (26)

Теперь умножим значение функции в точке M_i не на длину i-го отрезка, а на проекцию этого отрезка, скажем, на ось Ох, то есть на разность x_i – x_{i - 1} = x_i .

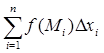Если существует конечный предел при интегральной суммы , не зависящий от способа разбиения кривой на отрезки и выбора точек M_i , то он называется криволинейным интегралом второго рода от функции f(M) по кривой L и обозначается

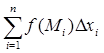. (27)

Подобным образом можно определить и криволинейные интегралы 2-го рода вида

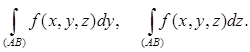
Если вдоль кривой L определены функции P(M)=P(x, y, z), Q(M) = Q(x, y, z), R(M) = R(x, y, z), которые можно считать компонентами некоторого вектора , и существуют интегралы

,

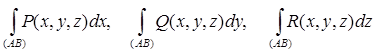тогда их сумму называют криволинейным интегралом второго рода (общего вида) и полагают

.

Если кривая L задана параметрическими уравнениями

x = (t), y = (t), z = (t), t ,

где , , – непрерывно дифференцируемые функции, то

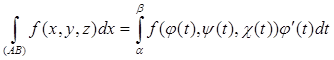. (28)

Связь между двойным интегралом и криволинейным интегралом 2-го рода задается формулой Грина:

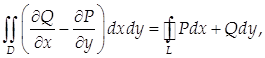(29)

где L – замкнутый контур, а D – область, ограниченная этим контуром.

Необходимыми и достаточными условиями независимости криволинейного интеграла

от пути интегрирования являются:

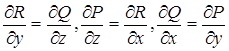. (30)

При выполнении условий (30) выражение Pdx + Qdy +Rdzявляется полным дифференциалом некоторой функции и. Это позволяет свести вычисление криволинейного интеграла к определению разности значений и в конечной и начальной точках контура интегрирования, так как

При этом функцию и можно найти по формуле

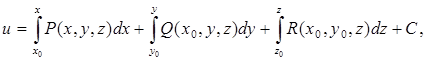(31)

где (x₀ , y₀ , z₀ ) – точка из области D, aC – произвольная постоянная.

2.2 Поверхностные интегралы

Рассмотрим некоторую поверхность S, ограниченную контуром L, и разобьем ее на части S₁ , S₂ ,…, S_п (при этом площадь каждой части тоже обозначим S_п ). Пусть в каждой точке этой поверхности задано значение функции f(x, y, z). Выберем в каждой части S_i точку

M_i (x_i , y_i , z_i ) и составим интегральную сумму

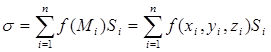
Если существует конечный предел при этой интегральной суммы, не зависящий от способа разбиения поверхности на части и выбора точек M_i , то он называется поверхностным интегралом первого рода от функции f(M) = f(x, y, z) по поверхности S и обозначается

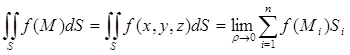. (32)

Если поверхность S задается явным образом, то есть уравнением вида z = (x, y), вычисление поверхностного интеграла 1-го рода сводится к вычислению двойного интеграла:

(33)

где – проекция поверхности S на плоскость Оху.

Разобьем поверхность Sна части S₁ , S₂ ,…, S_п , выберем в каждой части S_i точку M_i (x_i , y_i , z_i ), и умножим f(M_i ) на площадь D_i проекции части S_i на плоскость Оху. Если существует конечный предел суммы

,

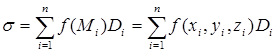не зависящий от способа разбиения поверхности и выбора точек на ней, то он называется поверхностным интегралом второго рода от функции f(M) по выбранной стороне поверхности S и обозначается

(34)

Подобным образом можно проектировать части поверхности на координатные плоскости Оxzи Оyz. Получим два других поверхностных интеграла 2-го рода:

и .

Рассмотрев сумму таких интегралов по одной и той же поверхности соответственно от функций P(x, y, z), Q(x, y, z), R(x, y, z), получим поверхностный интеграл второго рода общего вида:

(35)

Если D, D и D - проекции поверхности S на координатные плоскости Оху, Oxz и Oyz, то

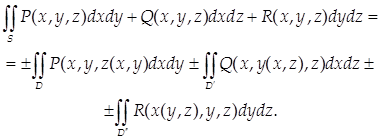(36)

Связь между тройным интегралом по трехмерной области V и поверхностным интегралом 2-го рода по замкнутой поверхности S, ограничивающей тело V, задается формулой Гаусса-Остроградского:

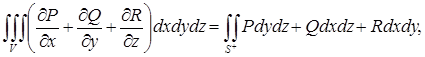(37)

где запись «S⁺ » означает, что интеграл, стоящий справа, вычисляется по внешней стороне поверхности S.

Формула Стокса устанавливает связь между поверхностным интегралом 1-го рода по поверхности и криволинейным интегралом 2-го рода по ограничивающему ее контуру с учетом ориентации поверхности:

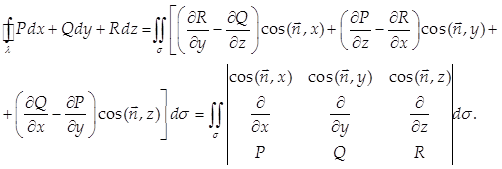(38)

2.3 Геометрические и физические приложения

1) Длина кривой.

Если подынтегральная функция f(x, y, z) 1, то из определения криволинейного интеграла 1-го рода получаем, что в этом случае он равен длине кривой, по которой ведется интегрирование:

(39)

2) Масса кривой.

Считая, что подынтегральная функция (x, y, z) определяет плотность каждой точки кривой, найдем массу кривой по формуле

(40)

Пример 6.

Найти массу кривой с линейной плотностью заданной в полярных координатах уравнением = 4, где

Решение.

Используем формулу (40) с учетом того, что кривая задана в полярных координатах:

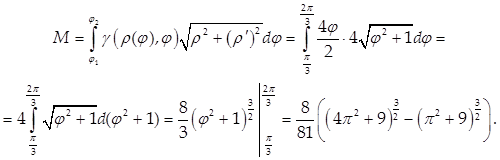
3) Моменты кривой l:

- (41)

- статические моменты плоской кривой l относительно осей Ох и Оу;

- (42)

- момент инерции пространственной кривой относительно начала координат;

- (43)

- моменты инерции кривой относительно координатных осей.

4) Координаты центра масс кривой вычисляются по формулам

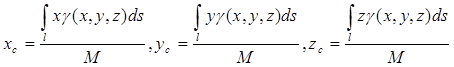. (44)

5) Работа силы , действующей на точку, движущуюся по кривой (АВ):

, (45)

Пример 7.

Вычислить работу векторного поля вдоль отрезка прямой от точки А(-2;-3;1) до точки В(1;4;2).

Решение.

Найдем канонические и параметрические уравнения прямой АВ:

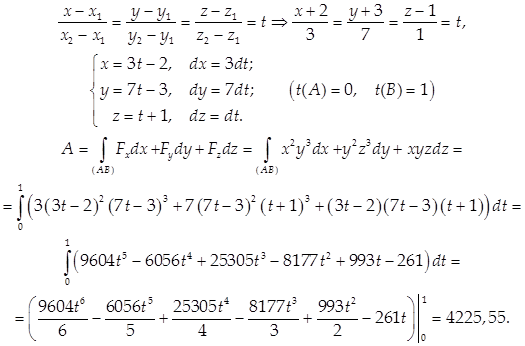
6) Площадь криволинейной поверхности, уравнение которой

z = f(x, y), можно найти в виде:

(46)

( – проекция S на плоскость Оху).

7) Масса поверхности

(47)

Пример 8.

Найти массу поверхности 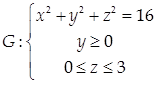с поверхностной плотностью = 2z² + 3.

Решение.

На рассматриваемой поверхности

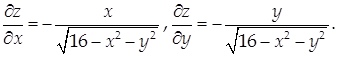Тогда

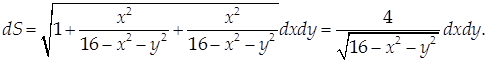
Проекцией D этой поверхности на координатную плоскость Оху является полукольцо с границами в виде дуг концентрических окружностей радиусов 3 и 4.

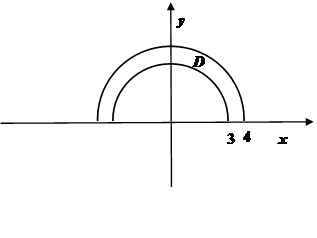
Применяя формулу (47) и переходя к полярным координатам, получим:

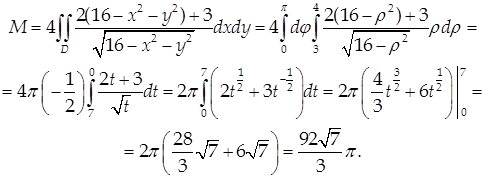
8) Моменты поверхности:

(48) статические моменты поверхности относительно координатных плоскостей Oxy, Oxz, Oyz;

(49)

- моменты инерции поверхности относительно координатных осей;

- (50)

- моменты инерции поверхности относительно координатных плоскостей;

- (51)

- момент инерции поверхности относительно начала координат

9) Координаты центра масс поверхности:

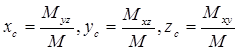. (52)

Список используемой литературы

1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. М.: Наука, 1999.

2. Кудрявцев Л.Д. Краткий курс математического анализа. М.: Наука, 2000.

3. Ильин В.А., Позняк Э.Г. Математический анализ. М.: Наука, 1999.

4. Смирнов В.И. Курс высшей математики.- Т.2. М.: Наука, 2005.

5. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М.: Наука, 2001.

6. Пискунов Н.С. Дифференциальное и интегральное исчисление. – Т.2. М.: Наука, 2001.

7. Сборник задач по математике для втузов. Специальные разделы математического анализа (под редекцией А.В.Ефимова и Б.П.Демидовича). – Т.2. М.: Наука, 2004.

8. Мышкис А.Д. Лекции по высшей математике. М.: Наука, 2003.

9. Титаренко В.И., Выск Н.Д. Кратные, криволинейные и поверхностные интегралы. Теория поля. М.: МАТИ, 2006.

Скачать архив с текстом документа