Математическая статистика
СОДЕРЖАНИЕ: Исследование сходимости рядов. Степенной ряд интеграла дифференциального уравнения. Определение вероятности событий, закона распределения случайной величины, математического ожидания, эмпирической функции распределения, выборочного уравнения регрессии.СОДЕРЖАНИЕ
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Задание 6
Задание 7
Задание 8
Задание 9
Задание 10
Задание 11
Задание 12
Задание 13
Задание 14
Литература
Задание 1. Исследовать сходимость рядов:
а) 
Решение:
Воспользуемся признаком Даламбера
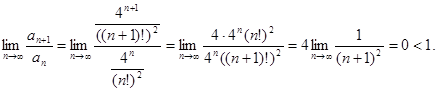
Ряд сходится.
б) 
Решение:
Для исследования этого ряда на сходимость удобнее применить радикальный признак Коши:
p =
=
=
=
= 
=5
Так как показатель Коши ряда строго больше единицы, то по радикальному признаку Коши ряд расходится.
Задание 2. Исследовать ряд на абсолютную и условную сходимость:
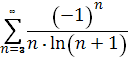
Решение:
Рассмотрим ряд из модулей:
Сравним его с рядом 
Мы сможем это сделать согласно признаку сравнения:
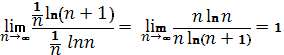
Ряд исследуем при помощи интегрального признака:
т.е. ряд расходится. Значит ряд из модулей тоже расходится, а наш знакопеременный ряд не обладает абсолютной сходимостью. Но он сходится условно согласно теореме Лейбница
|= 
Задание 3. Найти область сходимости ряда:
Решение:
Найдем интервал сходимости 
, где R – радиус сходимости. Найдем радиус сходимости R :
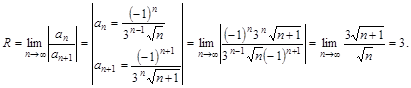
Следовательно, интервал сходимости ряда. Исследуем сходимость ряда на концах интервала:
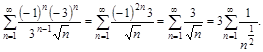
Полученный ряд является обобщенным гармоническим рядом, в котором
Следовательно, полученный ряд расходится.
Получили знакочередующийся ряд. Используем теорему Лейбница:
Значит, полученный ряд сходится.
Областью сходимости заданного ряда является промежуток 
.
Задание 4. Вычислить с точностью
= 0,001 
.
Решение:
Так как 83 является ближайшим к числу 520 кубом целого числа, то целесообразно число 520 представить в виде суммы двух слагаемых:
520 = 83 + 8.
Тогда
= 
= 8
= 8(1+0,001562)1/3
=
=8 =
= 8+ 0,0416-0,0002272+…
Третий член уже меньше чем 0,001, поэтому его следует отбрость и последующие за ним. Итак,
8 + 0,0416 8,0416
Задание 5. Найти три первых, отличных от нуля, члена разложения в степенной ряд интеграла 
дифференциального уравнения, удовлетворяющего следующему начальному условию:
Решение:
Воспользуемся разложением
Так как по условию х = 0, то будем иметь
Найдем коэффициенты при х:
;
, 
.
Подставляя найденные значения в формулу, получим
Задание 6. Среди 10 лотерейных билетов 6 выигрышных. Наудачу взяли 4 билета. Определить вероятность того, что среди них 2 выигрышных.
Решение:
Определимся с событием:
А – среди выбранных 4 билетов 2 выигрышных.
Вероятность этого события: 
Число всех элементарных исходов п ( число всех комбинаций выбора из 6 билетов по 2 билета ) равно числу сочетаний:
Число элементарных исходов т, благоприятствующих событию А :
Тогда, искомая вероятность равна:
Задание 7. В двух партиях 38% и 79% – процент доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них:
а) хотя бы одно бракованное;
б) два бракованных;
в) одно бракованное и одно доброкачественное?
Решение:
Определимся с событиями:
А1 – выбор доброкачественного изделия из первой партии,
выбор бракованного изделия из первой партии,
А2 – выбор доброкачественного изделия из второй партии,
выбор бракованного изделия из второй партии.
Тогда
.
а) А – хотя бы одно изделие бракованное.
б) В – оба изделия бракованные.
.
в) С – одно изделие доброкачественное и одно изделие бракованное.
.
Задание 9. Из 1000 ламп пi
принадлежит i-ой партии, i = 1, 2, 3, 
В первой партии 6%, во второй 5%, в третьей 4% бракованных ламп. Наудачу выбирается одна лампа. Определить вероятность того, что выбранная лампа – бракованная.
Решение:
Так как 
, то
Определимся с событиями:
А – выбрана бракованная лампа;
выбрана лампа i-ой партии, i = 1,2,3.
Найдем вероятности событий Вi :
п = 90 + 690 + 220 = 1000 ,
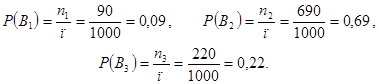
Найдем вероятности события А при условии, что события Bi ( i = 1,2,3 ) наступили, т.е. найдем вероятности выбора бракованной лампы при условии, что лампы взяты из 1-ой, 2-ой, 3-ей партий :
По формуле полной вероятности найдем искомую вероятность:
Задание 9. В магазин поступают однотипные изделия с трех заводов, причем i-й завод поставляет тi % изделий ( i = 1, 2, 3). Среди изделий i-го завода ni % первосортных. Куплено одно изделие. Оно оказалось первосортным. Определить вероятность того, что купленное изделие выпущено j-ым заводом.
.
Решение:
Определимся с событиями:
А – купленное изделие первосортное;
изделие выпущено i-ым заводом, 
.
Запишем вероятности событий Вi :
Запишем условные вероятности, т.е. вероятности того, что купленное изделие первосортное при условии, что оно выпущено i-ым заводом:
Вероятность того, что купленное первосортное изделие выпущено 1-ым заводом, вычислим по формуле Бейеса:
Задание 10. Вероятность наступления некоторого события в каждом из 100 независимых испытаний равна р = 0,8. Определить вероятность того, что число т наступлений события удовлетворяет следующему неравенству:
k1 = 75;
k2 = 90
Решение:
Воспользуемся интегральной теоремой Лапласа :
где Ф(х) – функция Лапласа,
Найдем х1 и х2 :
Учитывая, что функция Лапласа нечетная, т.е. 
, получим
.
По таблице найдем :
Искомая вероятность
Задание 12. Дискретная случайная величина Х принимает только два значения х1
и х2
, причем 
. Известна вероятность р1
= 0,7 возможного значения х1
, математическое ожидание М(Х ) = 1,3 и дисперсия D(X ) = 0,21. Найти закон распределения этой случайной величины.
Решение:
Сумма вероятностей всех возможных значений ДСВ равна 1. Отсюда вероятность того, что Х примет значение х2 равна
р2 = 1 – р1 = 1 – 0,7 = 0,3.
Запишем закон распределения ДСВ Х :
| Х | х1 | х2 |
| р | 0,7 | 0,3 |
Для нахождения значений х1 и х2 составим систему уравнений и решим ее:
или 
;
или 
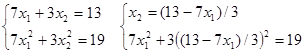
7x1
2
+ 
=19 (x 3)
70x1 2 -182x1 +112 = 0
По условию задачи 
. Следовательно, задаче удовлетворяет только решение 
, и искомый закон распределения будет иметь вид:
| Х | 1 | 2 |
| р | 0,7 | 0,3 |
Задание 12. Непрерывная случайная величина задана функцией распределения 
. Требуется найти:
а) функцию плотности распределения 
;
б) математическое ожидание 
;
в) дисперсию 
;
г) среднее квадратическое отклонение 
.
Построить графики функций и .
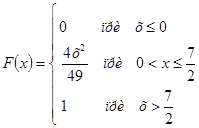
Решение:
а) Найдем функцию плотности распределения НСВ Х :
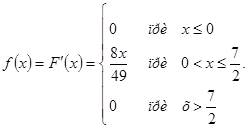
б) Найдем математическое ожидание НСВ Х :
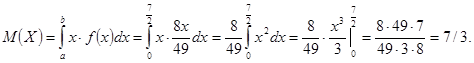
в) Найдем дисперсию НСВ Х :
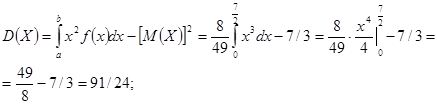
г) Найдем среднее квадратическое отклонение НСВ Х :
График функции распределения:
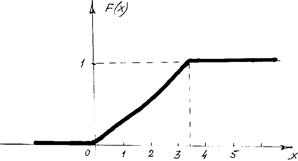
График функции плотности распределения:
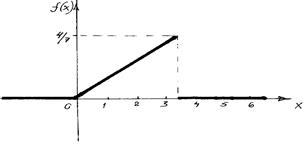
Задание 13. Задано статистическое распределение выборки. Требуется:
а) найти распределение относительных частот;
б) построить полигон относительных частот;
в) найти эмпирическую функцию распределения и построить ее график;
г) найти несмещенные статистические оценки математического ожидания, дисперсии и среднего квадратического отклонения в генеральной совокупности.
| xi | 1 | 3 | 4 | 6 | 7 |
| ni | 20 | 10 | 14 | 6 | 10 |
Решение:
а) Найдем объем выборки:
Относительные частоты определяем по формуле : 
Запишем распределение относительных частот :
| xi | 1 | 3 | 4 | 6 | 7 |
| wi | 0,33 | 0,17 | 0,23 | 0,1 | 0,17 |
Контроль: 
б) Построим полигон относительных частот:
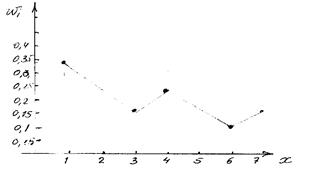
в) Эмпирическая функция
где 
число вариант, меньших х ;
п – объем выборки, может быть представлена в виде:
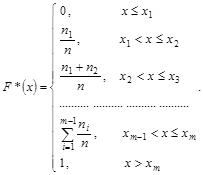
Тогда, искомая эмпирическая функция будет иметь вид :
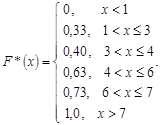
Строим график функции 
г) Несмещенной оценкой математического ожидания в генеральной совокупности является выборочная средняя:
Найдем эту оценку:
xв
= 
(120+310+414+66+710) =
= 3,53;
Несмещенной оценкой дисперсии в генеральной совокупности является исправленная выборочная дисперсия:
где DB – выборочная дисперсия.
Найдем выборочную DВ :
= 
= (400+300+784+216+700) – 12,46 = 27,54;
Найдем исправленную дисперсию, т.е несмещенную оценку генеральной дисперсии:
Несмещенной оценкой среднего квадратического отклонения в генеральной совокупности служит исправленное среднее квадратическое отклонение:
.
Найдем эту оценку:
.
Задание 14. Найти выборочное уравнение прямой линии регрессии Yна Х по данным, приведенным в корреляционной таблице
Х Y |
7 | 14 | 21 | 28 | 35 | 42 |
| 10 | 5 | 1 | - | - | - | - |
| 15 | - | 6 | 5 | - | - | - |
| 20 | - | - | 6 | 35 | 9 | - |
| 25 | - | - | 8 | 9 | 2 | - |
| 30 | - | - | - | 7 | 1 | 6 |
Решение:
Определим частоты 
, т.е. суммы частот появления значений у в каждой строке таблицы. Аналогично, найдем частоты 
. Очевидно, что 
, т.е. суммы частот равны объему выборки. В результате получим таблицу:
Х Y |
7 | 14 | 21 | 28 | 35 | 42 | ny |
| 10 | 5 | 1 | - | - | - | - | 6 |
| 15 | - | 6 | 5 | - | - | - | 11 |
| 20 | - | - | 6 | 35 | 9 | - | 50 |
| 25 | - | - | 8 | 9 | 2 | - | 19 |
| 30 | - | - | - | 7 | 1 | 6 | 14 |
| nx | 5 | 7 | 19 | 51 | 12 | 6 | n=100 |
Уравнение линейной регрессии Yна Х имеет вид:
,
где 
выборочный коэффициент корреляции.
Найдем значения параметров выборочного уравнения линии регрессии:
;
;
;
;
;
;
;
.
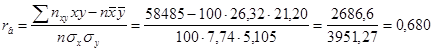Подставляем полученные значения параметров в выборочное уравнение регрессии:
.
Тогда выборочное уравнение регрессии примет окончательный вид:
.
ЛИТЕРАТУРА
1. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.2. – М.: Наука, 1985. – 506с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.2. – М.: Высшая школа, 1986. – 415с.
3. Доценко А.Д., Нагулин Н.И. Методические указания к практическим занятиям по курсу “Высшая математика” (Ряды). Харьков: ХИРЭ, 1992. – 38с.
4. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2000. – 400с.
5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2000. – 400с.