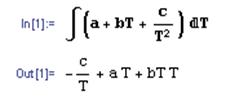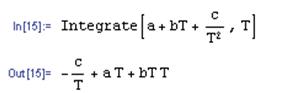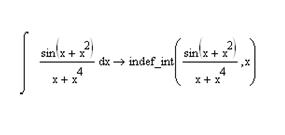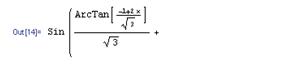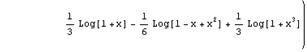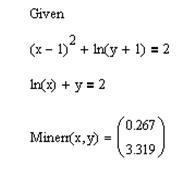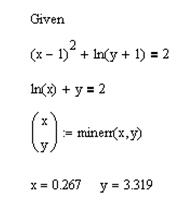«математические пакеты mathcad и mathematica в решении прикладных химических задач»

СОДЕРЖАНИЕ: Решение некоторых химических задачис помощью математических пакетов mathcad и mathematica 12

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Выпускная работа по
«Основам информационных технологий»

Магистрант кафедры

высокомолекулярных соединений

Фролов Александр Николаевич

Руководители:

к.х.н.. Костюк С.В.,

ассистент Шешко С.М.

Минск – 2009 г.

ОГЛАВЛЕНИЕ

[1] ].

1. ЗАРОЖДЕНИЕ И РАЗВИТИЕ СИСТЕМ СИМВОЛЬНОЙ

МАТЕМАТИКИ

Эру создания компьютерной символьной математики принято отсчитывать с начала 60-х годов. Именно тогда в вычислительной технике возникла новая ветвь компьютерной математики, не совсем точно, но зато броско названная компьютерной алгеброй. Речь шла о возможности создания компьютерных систем, способных осуществлять типовые алгебраические преобразования: подстановки в выражениях, упрощение выражений, операции со степенными многочленами (полиномами), решение линейных и нелинейных уравнений и их систем, вычисление их корней и т.д. При этом предполагалась возможность получения аналитических (символьных) результатов везде, где это только возможно.

К сожалению, книги по этому направлению были способны лишь отпугнуть обычного читателя и пользователя компьютера от изучения возможностей компьютерной алгебры в силу перенасыщенности их узкоспециальным теоретическим материалом и весьма специфического языка описания [ [2] ].

Большинство же пользователей заинтересовано в том, чтобы правильно выполнить конкретные аналитические преобразования, вычислить в символьном виде производную или первообразную заданной функции, провести аппроксимацию и т. д., а вовсе не в детальном и сложном математическом и логическом описании того, как это делается компьютером (или, точнее, его программистом).

Поняв это, многие западные фирмы приступили к созданию компьютерных систем символьной математики, ориентированных на широкие круги пользователей, не являющихся профессионалами в компьютерной алгебре. Учитывая невероятно большую сложность автоматизации решения задач в аналитическом виде (число математических преобразований и соотношений весьма велико, и некоторые из них неоднозначны в истолковании), первые подобные системы удалось создать лишь для больших ЭВМ. Но затем появились и системы, доступные для мини-ЭВМ.

Среди разработчиков математических систем долгое время бытовало мнение о вторичной роли пользовательского интерфейса и главенствующем значении математических возможностей таких систем. В результате в прошлом пользовательский интерфейс многих математических систем отличался ущербной простотой и архаичностью.

С переводом таких систем на ПК с графическими операционными системами класса Windows с таким подходом пришлось решительно кончать. Более того, превосходная цветная графика высокого разрешения современных ПК, о которой пользователи ЭВМ класса ЕС не могли и мечтать, резко повысила не только роль графического представления данных вычислений, но и привела к слиянию пользовательского интерфейса математических систем с интерфейсом современных графических операционных систем.

Система Maple V— патриарх в семействе систем символьной математики. И поныне это весьма привлекательная система для химика-аналитика и научного работника. Даже в среде MS-DOS Maple V имеет неплохой интерфейс и превосходно организованную обширную базу данных помощи. Полнота ядра системы, хранящего более 2700 математических функций и правил их преобразования, вполне заслуживает восторга и большого уважения. Весьма привлекательное свойство этой системы — подробная встроенная помощь и множество примеров ко всем встроенным в нее функциям и прикладным пакетам. Эти примеры легко скопировать в окно редактирования системы и тут же решить.

Достойна восхищения и математическая графика системы Maple, в частности возможность изображения пересекающихся трехмерных фигур с функциональной окраской. Новейшие системы Maple V для Windows по возможностям графики стоят на одном уровне с системами Mathematica 3/4. Считается, что они несколько превосходят системы Mathematica в части символьных преобразований, но такое превосходство на сегодня уже является весьма спорным.

К сожалению, фирма Waterloo Maple, Inc. (Канада) - разработчик системы Maple V — больше блистала математической проработкой своего проекта, чем уровнем его коммерческой реализации. В силу этого система Maple V была доступна в основном узкому кругу профессионалов. Сейчас эта фирма работает совместно с более преуспевающей в коммерции и проработке пользовательского интерфейса математических систем фирмой MathSoft, Inc. — создательницей весьма популярных и массовых систем для численных расчетов Mathcad, ставших международным стандартом для технических вычислений. Пока, однако, математические возможности этих систем в области компьютерной алгебры намного уступают системам Maple V, Mathematica 2 и даже малютке Derive (не говоря уже о реализациях Mathematica 3 и 4) [1, 2].

Появление новых версий Mathematica 3 и 4 вновь резко поднимает планку оценки качества систем компьютерной алгебры. Наступает новый этап интеграции математических систем как друг с другом, так и с современными текстовыми и табличными процессорами, такими как Word 2000/2003 и Excel 2000/2003 из офисных пакетов Microsoft Office 2000/2003.

2. ВВЕДЕНИЕ В ЧИСЛЕННЫЕ МЕТОДЫ

В данной главе представлена необходимая информация об основных численных методах, реализуемых на компьютере, которые будут использоваться в работе. Формулы приводятся для общего ознакомления, без вывода, акцент делается на понимание сущности метода.

2.1. Решение дифференциальных уравнений

Химику часто приходится иметь дело с процессами, параметры которых непрерывно меняются в зависимости от некоторой переменной. Эти явления обычно подчиняются законам, которые формулируются в виде дифференциальных уравнений y (x ) = f ( x ,y).

Одной из основных математических задач, которые приходится решать для таких уравнений, является задача Коши (или начальная задача). Эта задача возникает тогда, когда начальное состояние системы в точке x ₀ считается известным (y(x₀ )=y₀ ) и требуется определить ее поведение при x x ₀ .

В тех случаях когда невозможно найти аналитическое выражение y(x) (часто так и происходит), применяют численные методы. В основе их построения лежит тот или иной способ замены дифференциального уравнения y (x ) = f ( x , y) его дискретным аналогом.

Простейшим и исторически первым численным методом решения задачи Коши является метод Эйлера . В его основе лежит идея графического построения решения дифференциального уравнения. Этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.

Идея метода заключается в том, что промежуток [a, b] разбивается на конечное число n интервалов длиной h точками x ₁ , x ₂ ,… x_n , и площадь под кривой производной представляется в виде суммы площадей прямоугольников Таким образом, на малом промежутке h изменения независимой переменной x_i x x_i + h = x_{i +1} вместо интегральной кривой дифференциального уравнения y ( x ) берется касательная к ней

В результате неизвестная интегральная кривая заменяется приближенной к ней ломаной линией (ломаной Эйлера), для которой угловой коэффициент n- го звена равен f( x_n , y_n ) .

Метод Эйлера обладает невысокой точностью, имея лишь первый порядок аппроксимации: с изменением h ошибка вычислений также меняется пропорционально h . К тому же погрешность каждого нового шага, вообще говоря, систематически возрастает. Наиболее приемлемым для практики методом оценки точности является в данном случае метод двойного счета - с шагом h и шагом h /2. Совпадение полученных двумя способами результатов дает естественные основания считать их верными.

Гораздо более точным является метод Рунге-Кутты . Формулы для наиболее популярного алгоритма четвертого порядка имеют вид:

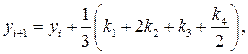
где коэффициенты k вычисляются как:

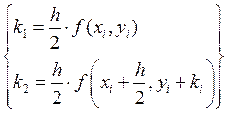
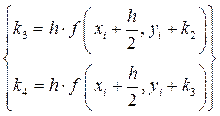
Для повышения точности расчета иногда применяется метод Рунге-Кутты с переменным шагом. В этом случае интервал разбивается на участки разной длины: там, где решение меняется слабо, шаги выбираются редкими, а в областях его сильных изменений - частыми. Это очень просто осуществить, так как алгоритм Рунге-Кутты является одношаговым и подразумевает простой пересчет при любом значении шага h_i искомого y( x_i + h_i ) через y ( x_i ). В результате применения адаптированного алгоритма для достижения одинаковой точности может потребоваться существенно меньшее число шагов, чем для стандартного метода Рунге-Кутты с фиксированным шагом.

Несмотря на кажущуюся универсальность, метод Рунге-Кутты «не работает» в случае так называемых жестких дифференциальных уравнений и соответствующих систем. Будьте осторожны в выборе метода, когда решаете, например, уравнение вида y (x )=-25y + cos(x ) + 25sin(x ), y(0) = 1, или анализируете кинети­ческую схему с сильно различающимися константами скорости, типичную для автокатализа. Если вместо красивых кинетических кривых метод Рунге-Кутты выдает не­понятные осцилляции, знайте: Вы столкнулись со случаем жесткой системы. Для решения требуется применение совсем иных алгоритмов, например неявных методов типа метода Булирша-Штера .

Основной идеей метода является вычисление состояния системы в точке x + h как результата двух шагов длины h /2, четырех шагов длины h /4, восьми шагов длины h /8 и так далее с последующей экс­траполяцией результатов. Метод строит рациональную интерполирующую функцию, которая в точке h /2 проходит через состояние системы после двух таких шагов, в точке h /4 проходит через состояние системы после четырех таких шагов, и т. д., а затем вычисляет значение этой функции в точке h = 0 , проводя экстраполяцию. Таким образом, проводится один шаг метода, после чего принимается решение, следует ли изменять шаг, а если да, то в какую сторону. При этом используется оценка погрешности, которую мы получаем в качестве дополнительного результата при рациональной экстраполяции [ [3] ].

2.2. Гармонический анализ и ряд Фурье

Теорема Фурье гласит, что любую зависящую от времени функцию можно представить в виде суммы синусов и косинусов с соответствующими весами (амплитудами). Таким образом, из общего «хора» сигналов преобразование Фурье выделяет отдельные «голоса», определяет их частоту и амплитуду. Математически можно сказать, что любая периодическая зависимость при определенных (и справедливых для любых реальных сигналов) допущениях может быть представлена бесконечным рядом Фурье. В тригонометрической форме он имеет вид:

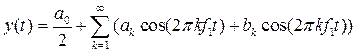
где a_k и b_k - косинусные и синусные коэффициенты Фурье. Они вычисляются по формулам:

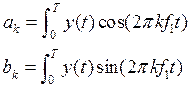
В этих выражениях k-номер гармоники, f₁ – частота первой гармоники, T= 1/f₁ – период колебаний.

Непериодические сигналы также могут иметь ряды Фурье. Но вместо дискретного спектра (из отдельных гармоник с номерами k=1,2,3,...) они имеют сплошной спектр [[4] ].

Применение преобразования Фурье произвело настоящий переворот в спектроскопии. Стало возможным регистрировать и обрабатывать ЯМР-, ИК- и УФ-спектры за несколько секунд или даже до-лей секунд, обеспечивая быстрый перевод первичного сигнала к привычному виду (Рис. 1). Конструкция приборов упростилась, а круг возможностей спектральных инструментов зачастую определяется вычислительной мощностью компьютера [ [5] ].

Рис. 1 - Сигнал спада свободной индукции (а) и полученный из него спектр ЯМР (б )

Смысл преобразования Фурье заключается в представлении функции в виде суммы периодических функций (синусоид). Основное применение преобразования Фурье в химии - перевод функции от времени в функцию от частоты:

Для численных расчетов был разработан быстрый и эффективный метод быстрого преобразования Фурье (БФП, в англоязычной литературе FFT - Fast Fourier Transform,), включенный во все серьезные математические программы. Смысл БФП заключается в разбиении массива точек на два подмассива и проведении преобразования Фурье над каждым в отдельности. Единственным ограничением БПФ является то, что длина набора данных должна быть равна целой степени двойки (т. е. можно обработать 512 точек, но не 511 или 513) [3, 5].

3. РЕШЕНИЕ НЕКОТОРЫХ ХИМИЧЕСКИХ ЗАДАЧ ИС ПОМОЩЬЮ МАТЕМАТИЧЕСКИХ ПАКЕТОВ MATHCAD И MATHEMATICA

Система Mathcad уже довольно длительное время является бесспорным лидером среди математического ПО с WYSIWYG (what you see is what you get) интерфейсом, максимально приближающим внешний вид документов к традиционным расчетам «на бумаге». Язык ввода формул прост и понятен интуитивно. К одному из главных отличий и достоинств пакета Mathematica следует отнести возможности получать решения сложных систем уравнений и функций в аналитическом виде, что не под силу Mathcad. Однако, работа в Mathematica требует не только высокого уровня владения пользователем лексики приложения, но и внимательного выполнения поставленной задачи.

Одной из главных задач настоящей работы является анализ возможности использования данных математических пакетов для решения типичных химических задач. Внимание также уделено оценке удобства в работе в средах обоих приложений.

3.1. Простые расчеты в Mathcad и Mathematica

Следует отметить, что изначально система Mathcad позиционировалась разработчиками как суперкалькулятор. Для примера использования данной системы в простых расчетах, попробуем посчитать какое-нибудь выражение, например, оценить константу равновесия для реакции паровой конверсии СО ( H = –41,17 Дж/моль, S = –42,09 Дж/моль*К) при температуре 600 K. Энтальпию и энтропию сорбции в первом приближении можно считать не зависящими от температуры.

Вводим следующее выражение:

exp(-(-41170+42.09*600)/600*8.314)=

На экране появится:

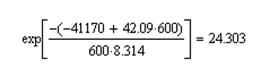
Рис. 2 - Вычисления в Mathcad

Как видно, форма записи максимально приближена к вычислениям «на бумаге».

Численный ответ выдается в виде десятичной дроби, с тремя знаками после запятой. Эти параметры можно изменить в меню “Format Result”. Представить ответ в виде натуральной дроби позволяет функция Fraction.

Несмотря на то, что ядро Mathcad предназначен для численного решения, он позволяет также производить и несложные символьные расчеты. Например, брать неопределенные интегралы типа интеграла зависимости теплоемкости от температуры a+bT+c/T² . Для этого следует ввести знак неопределенного интеграла (Ctrl+I либо с панели “Calculus”), записать уравнение и поставить после него вместо обычного знака равенства значок символьного решения “” (Ctrl+. либо с панели “Evaluation” [ [6] , [7] ]:

Рис. 3 - Вычисление неопределенного интеграла в Mathcad

Подобная задача легко выполняется и в пакете Mathematica с помощью функций Е или Exp

Рис. 4 - Вычисления в Mathematica

В отличие от Mathcad, пакет Mathematica великолепно проводит аналитические вычисления. Так предыдущий интеграл можно взять, используя соответствующую пиктограмму из палитры (Рис. 5(а )) или с помощью функции Integrate (Рис. 5(б ) ) [1, 2]:

а	б

Рис. 5 – Вычисление неопределенного интеграла в Mathematica

Следует также указать, что для решения задач в аналитическом виде использование пакета Mathematica предпочтительнее. Например, более сложный интеграл 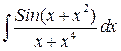Mathcad уже взять не в состоянии (Рис. 6(а )), в отличие от Mathematica (Рис. 6(б )):

а	б

Рис. 6 - Вычисление неопределенного интеграла: а – в среде Mathcad (интеграл вычислить

нельзя: приложение выдает indef_int(f(x), x)); б – в среде Mathematica

Удобнее записать уравнение в параметрическом виде и, меняя значение параметров, получать разные ответы. Например, записав один раз формулу:

и меняя значения Т, можно получить значения К_р при разной температуре.

Для этого сначала необходимо определить переменные. В Mathcad есть несколько особенностей определения переменных:

· Оператор присвоения (:=) вводится нажатием двоеточия “:” либо, если переменная не используется системой, нажатием знака равенства “=”. Оператор присвоения определяет переменную только для расчетов, идущих ниже.

· оператор глобального присвоения (), вызываемый нажатием “~”.применяется, если требуется определить переменную для использования во всем документе [6].

Введем следующие выражения:

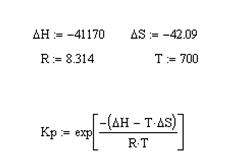
Рис. 7 – Решение выражения с присвоением переменных в Mathcad

Здесь подстрочный символ для К_р вводится нажатием точки “.”, а символы можно взять мышкой с панели “Greek” или набрать заглавную D и нажать Ctrl+G. Сочетание клавиш Ctrl+G превращает стоящую впереди букву в символ греческого алфавита.

Переменным можно присваивать любые имена, но без пробелов. Задавать значения переменной можно не только численно. Например, выбрав на панели “Controls” инструмент “Slider” (Рис. 8) и присвоив его переменной а. Теперь, передвигая движок, можно изменять значения а, что весьма удобно и наглядно.

Рис. 8 – Присвоение переменной в Mathcad с помощью инструмента Slider

Диапазон значений (по умолчанию от 0 до 100) можно менять, кликнув по движку правой кнопкой мыши и выбрав “Mathsoft Slider Control Properties”.

Mathematica выполняет описанные выше операции также легко и удобно.

Принципиального отличия в присвоении переменной значений в Mathematica нет. Если выражение использует «=» или функцию Set [] , программа немедленно заменяет переменную на установленное значение. Выражение «:=» или SetDelayed возвращает значение, когда функция вызывается. Решение представленной задачи в Mathematica будет иметь вид:

Рис. 9 - Решение выражения с присвоением переменных в Mathematica

3.2. Решение функциональных уравнений и построение графиков

Уравнения с параметрами очень удобны, если требуется вычислить лишь одно или несколько значений функции. Но что если нам требуется вычислить значения функции в ста точках и построить график? Можно, конечно постараться, сто раз подставляя значения аргумента и записывая значения функции, но это – весьма нерационально.

Пусть, например, перед нами стоит задача вычислить энтальпию образования кальцита CaCO₃ в диапазоне температур 300-1000 K. Здесь, очевидно, нам придется воспользоваться эмпирической зависимостью теплоемкости от температуры:

Сначала запишем значение энтальпии при 298 К (Н₂₉₈ ) и определите область значений независимой переменной Т (температура). В Mathcad это выглядит следующим образом: имя переменной, оператор присвоения, первое число диапазона, запятая, второе число диапазона, «многоточие» последнее число диапазона. Многоточие вводится через символ точки с запятой “;”. Итак, в данном случае выражение для ввода Т будет следующим:

T:=300,325..1000

Второе число диапазона вводится для определения шага изменения переменной (в нашем случае 25 градусов). Если не вводить его, Mathcad будет по умолчанию считать с дискретизацией 1 (300, 301, 302…).

Теперь определите теплоемкость как функцию от температуры. В Mathcad запись абсолютно аналогична написанию на бумаге С_p (T). Теперь при вызове значений С_р через

C.p=

Mathcad возвращает ответ С_р =function, что позволяет Вам рассчитать значение С_p для любой температуры Т. Так, например, для температуры 300 K рассчитывается С_p (200) = 44,054:

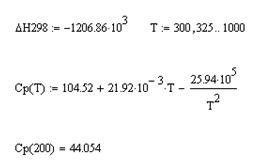
Рис. 10 – Решение функционального уравнения в Mathcad

Теперь определим энтальпию как функцию температуры. Для вставки значка определенного интеграла воспользуйтесь панелью “Calculus” либо нажмите символ “” (Shift+7).

Выбор метода численного интегрирования по умолчанию возложен на программу. Тем не менее, кликнув правой кнопкой мышки по значку интеграла, можно выбрать в контекстном меню один из четырех имеющихся методов.

Для построения графика можно либо выбрать в меню “Insert Graph” пункт “X–Y Plot” либо нажать знак “@” (“Shift+2”). По оси абсцисс укажите имя независимой переменной (в данном случае Т), по оси ординат – имя функции (Н(T)) (Рис. 11). Также можно построить. не зависимость H(T) от Т, а, например, зависимость ln(H(T)) от 1/Т. Все, что для этого нужно, – поменять подписи по осям, Mathcad поймет, чего мы хотим [6, 7].

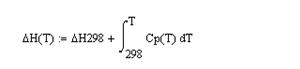
Рис. 11 – Построение графика функции H(T) в Mathcad

Для построения графиков в другой программе (Excel, Origin) можно вызвать столбцы значений Т и H(T) и скопировать их в буфер обмена.

Данная задача решается в Mathematica также с присвоением значений необходимых переменных и и дальнейшего интегрирования (Рис. 12). Для построения графика, в отличие от Mathcad, в котором график строится наглядно при назначении переменной (по оси Х) и функции (по оси Y), нужно воспользоваться дополнительной функцией Plot [ Evaluate []] с указанием диапазона значений переменной и функции:

Рис. 12 - Решение функционального уравнения и построения графика функции в Mathematica

В целом, построение графиков простых зависимостей проще выполнять в Mathcad, благодаря более удобному интерфейсу.

3.3. Решение трансцендентных уравнений

Уравнения, содержащее трансцендентные функции (показательные, тригонометрические, логарифмические, обратные тригонометрические) от неиз-

вестного (переменного), например, , и системы подобных уравнений,

весьма распространены в химической термодинамике. В аналитическом виде подобные уравнения не решаются, а метод последовательных приближений очень трудоемок и не всегда обеспечивает приемлемую точность. Посмотрим, чем может в данном случае помочь Mathcad.

Пусть требуется найти температуру, при которой давление паров воды составляет ровно 5,00 атм., не пренебрегая зависимостью энтальпии и энтропии от температуры.

Необходимо определить переменные: оценку ожидаемой температуры, теплоемкость, энтальпию и энтропию образования жидкой и твердой воды и записать уравнение для давления пара, как это сделано на рисунке 13. Здесь индекс “liq” относится к параметрам жидкой воды, индекс “gas” – газообразной. При первоначально выбранной температуре 150 ^о С давление насыщенного пара равно 4,4 атм, значит, верное значение где-то близко.

Можно подбирать Т , следя за изменением Р , а можно сделать удобнее и быстрее. Для решения уравнений и систем уравнений в Mathcad используется блок решения “given – find” (“дано – найти”). Запишем слово given, под ним введем наше условие: выражение для давления насыщенного пара, знак «булева равенства =» и требуемое значение этого выражения, т. е. 5 (Рис. 13). Теперь скомандуем программе «найди решение относительно Т », для этого вводим строчку [6]:

find(T)=

Полученный ответ и будет корнем уравнения:

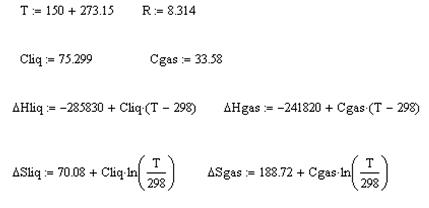
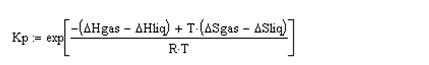
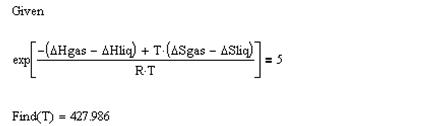
Рис. 13 – Решение трансцендентного уравнения в Mathcad

Для решения приведенного трансцендентного уравнения в среде Mathematica можно использовать функцию Solve[] :

Рис. 14 - Решение трансцендентного уравнения в Mathematica

Проверка показывает, что найденное значение температуры найдено верно:

Рис. 15 – Проверка достоверности найденного решения в Mathematica

3.4. Решение системы уравнений

Для решения уравнений в Mathcad применяется блок решения “given – find” применяется и для систем уравнений. В этом случае ответ будет представляться в виде столбца значений и вызываться функцией find(x,y,x…) либо minerr(x,y,x…), где в скобках через запятую перечисляются имена переменных, относительно которых надо решить систему (Рис 16, а ).

x:= 1 y:= 2	x:= 1 y:= 2
а	б

Рис. 16 – Решение системы уравнений в Mathcad

Можно создать переменные, которым бы мы присвоили значение ответа:

вставить матрицу из n строк и одного столбца (n – количество переменных) и присвоить ей значение minerr(x,y,z…) (Рис 16, б ), это делается с помощью раздела меню “Insert Matrix” или сочетания клавиш “Ctrl+M” [7]

В среде Mathematica воспользуемся функциями: Solve и FindRoot

При использовании функции Solve появляется ошибка, которая говорит о том, что пакет Mathematica не может решить это трансцендентное уравнение алгебраическим методом, т.е. аналитически (This transcendental equation cannot be solved by algebraic methods):

Рис. 17 – Отсутствие аналитического решения для системы уравнений в Mathematica

Следовательно, нужно использовать функцию FindRoot и решать уравнение численно по аналогии с решением в Mathcad:

Рис. 18 – Численное решение системы уравнений в Mathematica

Для проверки полученных корней выполним подстановку в систему и убедимся, что решение верное:

Рис .19 - Проверка достоверности найденных решений системы уравнений в Mathematica

3.5. Дифференциальные уравнения

Численное решение дифференциальных уравнений широко применяется для быстрого и точного решения прямой кинетической задачи: определения зависимости концентраций веществ от времени при заданных начальных концентрациях и скоростях.

Для решения дифференциальных уравнений предусмотрены функции odesolve, rkadapt, rkfixed, bulstoer, а также некоторые другие. Подробную информацию о применимости каждого алгоритма можно найти в разделе Help под названием “differential equation solvers”. Остановимся пока на функции rkfixed. Данная функция интегрирует дифференциальные уравнения и их системы методом Рунге-Кутты четвертого порядка с постоянным (fixed) шагом и может применяться для несложных кинетических схем. К сожалению, эта функция требует специфического ввода условия [[8] , [9] ].

Пусть имеется простейшая кинетическая схема

Известны значения констант скорости (k1 =0,1 с-¹ , k2 =0,05 с-¹ ) и начальных концентраций реагентов (A₀ =1 М, B₀ =0 М, C₀ =0 М). Требуется найти, как будут изменяться концентрации этих веществ во времени в течение 100 секунд.

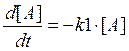По закону действующих масс зависимость концентраций реагентов от времени можно записать в виде системы дифференциальных уравнений:

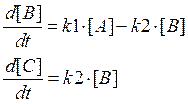
Сначала определим значения констант скорости k1=0,1 и k2=0,05, начальный и конечный моменты времени t0=0 и t1=100, а также число точек N=1000 в интервале [t0, t1], в каждой из которых программа будет искать решение. Затем запишем вектор кинетических уравнений C(t,Y), где Y – массив концентраций, Y₀ , Y₁ и Y₂ – концентрации веществ А, В и С соответственно, а также вектор начальных значений C0. Теперь присвоим матрице решений S значение rkfixed (вектор уравнений, начальное значение независимой переменной, конечное значение независимой переменной, число точек, начальные условия) (Рис. 20).

Если теперь вызвать S , то предстанет матрица из 1000 строчек и 4 столбцов. Первый столбец – значения времени, второй, третий и четвертый – соответствующие значения концентраций. Отдельно столбцы можно вызвать, как это показано на Рис.20, с помощью верхнего индекса A:=S¹ . Верхний индекс ставится через “Ctrl+6” или кнопку “Matrix Column” панели “Matrix”.

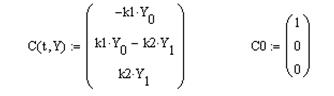
Рис. 20 – Численное решение системы дифференциальных уравнений с помощью

функции rkfixed в Mathcad

Осталось только построить график (Рис. 21), и прямая кинетическая задача решена:

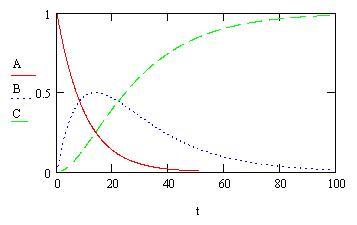
Рис. 21 – Графическое решение системы дифференциальных уравнений в Mathcad

Функция rkadapt требует такого же синтаксиса, но решает уравнения методом Рунге-Кутты с переменным шагом, анализируя скорость изменения решения. Функция bulstoer реализует метод Булирша-Штера (Bulirsch-Stoer Method) для так называемых жестких систем.

Эти функции удобны в работе и при наличии некоторого опыта затруднений с вводом условия не возникает. Но для тех, кто предпочитает бльшую наглядность, предусмотрена функция odesolve, работающая в блоке решения.

Решим с ее помощью ту же задачу. Точно так же определите вначале константы скорости и временной интервал. Затем запишем блок решения с тремя дифференциальными уравнениями и граничными условиями (Рис. 22).

Дифференциал вводится через нажатие клавиш “Shift+/” либо из па-

нели инструментов “Calculus”; также можно пользоваться значком производной “ ’ ” (вызывается нажатием “Ctrl+F7”). После того, как записаны все уравнения, вызовите функцию odesolve (вектор переменных, независимая переменная, конечное значение). Полученную зависимость концентрации от времени можно вывести на график либо вызвать в виде столбца значений для переноса в другую программу.

,

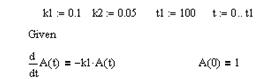
Рис. 22 – Решение системы дифференциальных уравнений с помощью функции

odesolve в Mathcad

Выбор метода численного решения также оставляется на усмотрение пользователя. Если кликнуть правой кнопкой мыши на функцию odesolve, появится контекстное меню, в котором можно выбрать метод (с фиксированным и адаптирующимся шагом, а также stiff-метод для жестких систем). Для простых систем результат одинаков, но в случае сложной системы (автоколебания), возможно, придется задуматься о методе интегрирования.

В пакете Mathematica подобные дифференциальные уравнения в численном виде нужно решать с помощью функции NDSolve . В результате получаем интерполяции трех функций для значений t от 0 до 100. С помощью функции Plot [ Evaluate [ ]] строим зависимости графически (Рис. 23):

Рис. 23 – Решение системы дифференциальных уравнений в Mathematica

Для проведения физико-комических расчетов часто применяется подход, направленный на упрощение математических моделей, основанный на использовании различных приближений химической кинетики. Одним из наиболее распространенных приближений является метод квазистационарных концентраций. Метод применим для описания многостадийных реакций, на определенных стадиях которых образуются промежуточные вещества (интермедиаты) с высокой реакционной способностью (при кинетическом описании цепных [[10] ] и ферментативных [[11] ] реакций). Условием применимости метода является малое время жизни интермедиатов по сравнению с временем, за которое состав реакционной системы успевает значительно измениться (условие Христиансена). Принимается, что производные концентраций активных промежуточных частиц по времени равны нулю (теорема Боденштейна).

Таким образом, в системе уравнений, входящих в математическую модель, некоторые дифференциальные уравнения могут быть заменены на алгебраические. Кинетический анализ механизма реакции в этом случае существенно облегчается. Например, механизм термического разложения ацетальдегида CH₃ CHO в определенных условиях может протекать по цепному механизму, включающему следующие стадии [[12] ]:

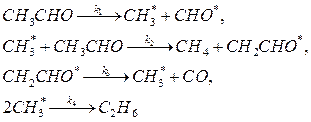
(Промежуточные интермедиаты помечены звездочкой.)

Рассмотрим решение поставленной задачи с помощью редактора Mathcad. Так, скорость расходования ацетальдегида составляет:

Как видно, в выражение входит концентрация нестойких радикалов . Если из вектора правых частей системы уравнений для математической модели экстрагировать строки, относящиеся к производным и , составить из них систему алгебраических уравнений и решить ее путем умножения на обратную матрицу, то можно выразить концентрации указанных интермедиатов через концентрации стабильных участников реакции:

Рис. 24 – Анализ кинетической модели в приближении квазистационарности в Mathcad.

Поскольку отрицательные корни уравнения не имеют смысла, и их мы отбрасываем, получаем , что стационарная концентрация радикалов равна:

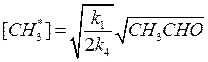
После подстановки полученного выражения в уравнение скорости расходования ацетальдегида получаем окончательное выражение, в которое входят концентрации только стабильных компонентов:

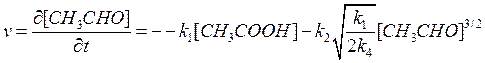
Аналогично получаем уравнения скоростей образования метана, оксида углерода и этана:

Весьма важно, что скорости накопления или расхода всех стабильных веществ, участвующих в процессе, зависят лишь от текущей концентрации ацетальдегида.

Рассмотрим решение данной задачи с помощью пакета Mathematica. Принцип нахождения остается прежний. Решение осуществляли с помощью функции Solve . Как видно из рис. 25 Mathematica легко находит корни заданных уравнений и при этом ответ выдается в более наглядной форме, что может быть удобнее при произведении расчетов обычным химиком, не владеющим в совершенстве математическим аппаратом:

Рис. 25 – Анализ кинетической модели в приближении квазистационарности в Mathematica.

Дальнейшие выводы формул зависимостей концентраций промежуточных интермедиатов от концентрации стабильных компонентов приведены выше.

3.6. Быстрое преобразование Фурье

Рассмотрим функции математических пакетов Mathcad и Mathematica которые позволят нам производить прямое и обратное преобразования Фурье для рассматриваемого примера реального сигнала спада свободной индукции ЯМР. Для начала зададим периодическую функцию в виде суперпозиции синусов:

где: , , и равны 1, 2 и 3, а соответствующие амплитуды 1, 2 и 1 соответственно.

Для применения БПФ в среде Mathcad требуется представить данные в виде векторов времени и значений функции от времени. Число счетных точек N=1024 (число N должно быть целой степенью двойки: 128, 256, 512 и т. п.), временной промежуток =10 и шаг изменения времени dt=/N. Теперь определяем массив k=0..N и вектор времени t_k =k*dt (рис. 26) [6].

Рис.26 – Сумма трех синусоид с разными частотами и амплитудами (построение в Mathcad )

В среде Mathcad быстрое преобразование Фурье осуществляют функции fft, и cfft, вектор ответов вызывается командой, например, F:=fft(y). Сейчас наш вектор F является функцией от точки счета. Для его перевода в функцию от частоты введем дополнительный вектор и построим для наглядности график (Рис. 27). Получились три пика при частотах, близких к 1, 2 и 3 и с соотношением амплитуд 1:2:1, как и было заданно.

Рис. 27 – Прямое преобразование Фурье в Mathcad

Для того чтобы убедиться в справедливости полученные результатов (Рис. 26) можно воспользоваться обратным преобразование Фурье. Для этого воспользуемся встроенной функцией ifft (Inverse Fast Fourier Transform). После данной процедуры должна получиться зависимость, идентичная той, которая представлена на рис. 28.

Рис. 28 – Обратное преобразование Фурье в MathCad

Данные процедуры можно также проделать и в пакете Mathematica. Для начала определим переменную y[t] в виде суммы трех синусов и построим график этой зависимости (рис. 29):

Рис. 29 – Сумма трех синусоид с разными частотами и амплитудами (построение в Mathematica)

Соответствующей функцией для прямого преобразования Фурье является FourierTransform . Однако, в отличие от функции fft пакета Mathcad, выходным параметром функции FourierTransform является аналитическое решение выражения:

Рис. 30 – Прямое преобразование Фурье в Mathematica

Как видно из рисунка 30 аналитическое решение содержит дельта функцию (DiracDelta), которую Mathematica не может отобразить графически. Чтобы убедиться в справедливости выражения, сделаем обратное преобразование Фурье от полученного аналитического выражения. Для этого воспользуемся функцией InverseFourierTransform, представив обратное преобразование Фурье графически, и убедимся в идентичности графика на рисунке 31 и на рисунке 29. Данная функция также позволяет получить аналитическое выражение преобразуемой функции:

Рис. 31 – Обратное преобразование Фурье в Mathematica

ЗАКЛЮЧЕНИЕ

Информационные технологии представляющие собой современные средства обработки и визуализации получаемой информации, становятся неотъемлемым инструментарием исследователя любой области современного знания. Математические пакеты, представляющие собой удобные и многофункциональные прикладные программы, помогают реализовывать численные эксперименты, решать сложные системы уравнений, получаемые при описании химико-физических процессов, визуализировать полученные данные.

При выполнении выпускной работы проведен анализ возможности применения математических пакетов Mathcad 12.0 и Mathematica 5.0 при решении наиболее типичных химических задач, требующих математической обработки результатов. С помощью указанных приложений были разобраны примеры решения простых функциональных уравнений, трансцендентных и дифференциальных уравнений для расчета скоростей изменения концентраций компонентов реакционных сред, а также рассмотрены возможности математических пакетов в проведении прямого и обратного Фурье преобразования.

В результате проделанной работы можно заключить, что математические пакеты Mathcad и Mathematica эффективно справляются с поставленными задачами интегрирования, численного решения простых и дифференциальных уравнений. Стоит отметить, что для получения результата в аналитическом виде, предпочтительнее использовать Mathematica, поскольку Mathcad проводит решение численными методами, в то время как осуществление Фурье преобразований для получения спектров ядерного магнитного резонанса, Mathcad, наоборот, более эффективен при построении графических решений. В заключение следует добавить, что пользовательский интерфейс среды Mathcad несколько удобен по сравнению с Mathematica, однако выбор программы, конечно, остается за исследователем.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ К РЕФЕРАТУ

Maple V................................................................................ 6

Mathcad 2, 4, 6, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 22, 23, 25, 26, 27, 28, 29, 31, 33

Mathematica 2, 4, 6, 11, 12, 13, 14, 16, 17, 18, 19, 20, 23, 24, 26, 27, 29, 30, 31, 33

метод Булирша-Штера................................................. 22

метод Рунге-Кутты........................................................... 8

Метод Эйлера.................................................................... 7

преобразование Фурье ..................... 2, 9, 27, 28, 29, 30

ряд Фурье ........................................................................ 2, 9

ЭВМ................................................................................. 5, 6

ИНТЕРНЕТ РЕСУРСЫ В ПРЕДМЕТНОЙ ОБЛАСТИ ИССЛЕДОВАНИЯ

http://www.sciencedirect.com

На сайте можно найти практически все статьи по научной тематике, однако полные версии статей в основном платные.

http://www.elsiever.com

Данный сайт аналогичен предыдущему, однако упор тут делается на медико-биологические журналы. Опять таки доступ только к abstracts, но иногда открывают и полный доступ.

http://www.springerprotocols.com

Сайт содержит большую электронную базу данных протоколов лабораторных исследований в биомедицинских науках и науках о жизни. Для получения полных версий журналов необходима подписка.

http://www.abc.chemistry.bsu.by/current/trialjournal.html

Сайт создан доцентом химического факультета БГУ и представляет собой каталог, в котором собрана информация об известных нам химических научных журналах, предоставляющих бесплатный доступ к полным текстам опубликованных статей.

http://www.e-library.com

Российская электронная библиотека, где можно найти множество статей, но в основном российских изданий.

http://www.chem.msu.ru

Химическая информационная сеть (Россия). Электронные версии журналов, базы данных, олимпиады и конкурсы научных работ, и т.д. и т.п.

http://www.lipidsonline.org/

Ресурс онлайн для пациентов, исследователей и педагогов с интересом в атеросклерозе, дислипидемии и обменом липидов.

http://www.lipidlibrary.co.uk

На сайте представлены документы, содержащие информацию и опыт, полученные в шотландском научно-исследовательском институте (Scottish Crop Research Institute):определения, структуры, состав, возникновение, биохимия и функции большинства типов жирных кислот и липидов.

http://www.sigmaaldrich.com/

Портал одного из крупнейших в мире поставщиков химических реактивов и лабораторного оборудования. Огромное множество соединений, предлагаемых на продажу.

http://www.biochemweb.org/

Этот сайт предоставляет собой виртуальную библиотеку в областях биохимии, молекулярной и клеточной биологии. В то время как многие из ресурсов, перечисленных на этих страницах, разработаны для ученых, однако есть ресурсы, которые не требуют такого уровня подготовки, они помечены как Beginners Level.

http://www.rsc.org/

Сайт RSC (Royal Society of Chemistry) – самой большой организации в Европе, продвигающей химические науки. Здесь представлена информация в области химии для учителей, лекторов, студентов, которая включает в себя библиотеку, большой диапозон журналов, книг, баз данных, а также конференции и события в мире.

http://www.iupac.org/dhtml_home.html

Официальный сайт Международного Союза Теоретической и прикладной Химии (International Union of Pure and Applied Chemistry) - организации, которая поддерживает мировое взаимодействие в химической науке, и признана в качестве мировой авторитет по таким темам как: химическая номенклатура, терминология, стандартные приемы измерения и атомные массы. 1200 химиков по всему миру включены в работу Союза по 8 направлениям. Здесь можно найти руководства или рекомендации по выполнению тех или иных операций в химии, по терминологии и классификации химических соединений. Организацией ежемесячно издается журнал «Pure And Applied Chemistry»; на сайте бесплатно доступны статьи из этого журнала. Поиск информации осуществляется по ключевым словам, а также авторам статьи, ее названию и году издания.

ВОПРОСЫ К ТЕСТАМ ПО ИТ

1) Тег IMG предназначен:

a) для отображения на веб-странице изображений в графическом формате GIF, JPEG или PNG

b) для отображения на веб-странице изображений только в графическом формате GIF

c) для отображения на веб-странице изображений только в графическом формате JPEG

d) для отображения на веб-странице изображений только в графическом формате PNG

(Правильный ответ а).

question type=close id=93

text Тег IMG предназначен:/text

answers type=request

answer id=313759 right=1 Для отображения на веб-странице изображений в графическом формате GIF, JPEG или PNG /answer

answer id=313760 right=0 для отображения на веб-странице изображений только в графическом формате GIF./answer

answer id=313761 right=0 для отображения на веб-странице изображений только в графическом формате JPEG /answer

answer id=313762 right=0 для отображения на веб-странице изображений только в графическом формате PNG /answer

/answers

/question

2) С помощью какой программы можно рисовать структуры химических соединений:

a) Origin

b) MathType

c) ISIS Draw

d) Paint

(Правильный ответ c).

question type=close id=493

text С помощью какой программы можно рисовать структуры химических соединений:/text

answers type=request

answer id=313759 right=0Origin/answer

answer id=313760 right=0MathType/answer

answer id=313761 right=1ISIS Draw/answer

answer id=313762 right=0Paint/answer

/answers

/question

ДЕЙСТВУЮЩИЙ ЛИЧНЫЙ САЙТ В WWW

http://chem-lab617.narod.ru

ГРАФ НАУЧНЫХ ИНТЕРЕСОВ

магистранта Фролова А.Н. химический факультет.

Специальность “Химия”

Смежные специальностиь 02.00.03 – органическая химия .Органический синтез. 2.Качественный и количественный анализ органических веществ и установление их строения. 02.00.08 –химия элементорганических соединений 1.Синтез элементорганических соединений

Основная специальность 02.00.06 – высокомолекулярные соединения Синтез, анализ, исследование структуры, свойств и превращений высокомолекулярных соединений.

Сопутствующие специальности 02.00.02 – аналитическая химия 1. Выявление и исследование химических и физических свойств веществ, используемых для их разделения и концентрирования. 02.00.04 – физическая химия 1.Исследование зависимостей свойств химических систем от состава и структуры. 2.Разработка общих принципов и методов изучения процесса изменения состояния химических систем во времени. Исследование закономерностей процессов изменения структуры и состава химических систем (кинетика и механизм химических реакций, каталитических процессов).

ПРЕЗЕНТАЦИЯ МАГИСТЕРСКОЙ РАБОТЫ

Презентацию, выполненную в Power Point в цветном варианте, можно посмотреть по следующей ссылке: http://chem-lab617.narod.ru/presentation.rar

СПИСОК ЛИТЕРАТУРЫ К ВЫПУСКНОЙ РАБОТЕ

[1] . Воробьев Е.А. Введение в систему символьных, графических и численных вычислений Математика-5 / М.: Диалог-МИФИ, 2005. – 368 с.

[2] . Дъяконов В.П. Mathematica 4.1/4.2/5.0 в математических и научно-технических расчетах / M.: СОЛОН-Пресс, 2004 г. – 696 с.

[3] . Фихтенгольц Г. М. Основы математического анализа: В 2-х т. / М.: Физматлит, 2002. – 856 с.

[4] . Самарский А. А. Введение в численные методы. / СПб.: Лань, 2000. - 736 с.

[5] . А.Т.Лебедев Масс-спектрометрия в органической химии / М:: БИНОМ. Лаборатория знаний, 2003. – 493 с.

[6] . Васильев A.H. Mathcad 13 на примерах / С-Пб.: БХВ-Петербург, 2006. – 512 с.

0[7]. Ивановский Р.И. Компьютерные технологии в науке и образовании. Практика применения систем MathCAD / М.: Высшая школа, 2003.- 431с.

[8] . Ортега Дж., Пул У. Введение в численные методы решения дифференциальных уравнений. / М.: Наука, 1986. – 288 с.

[9] . Солодов А.П., Очков В.Ф. Mathcad. Дифференциальные модели / М.: МЭИ, 2002. – 239 с.

[10] . Семенов Н. Н. Цепные реакции. / М.: Наука, 1986. – 535 с.

[11] . Бенсон С. Основы химической кинетики / М.: Мир, 1964. – 604 с.

[12] . Коробов В. И. Математические пакеты в химических расчетах: прямая задача химической кинетики. // Exponenta Pro. Математика в приложениях – 2004, № 3-4 – с. 115-121

Скачать архив с текстом документа