Механічні й електромагнітні коливання
СОДЕРЖАНИЕ: Поняття гармонічних коливань, їх сутність та особливості, основні характеристики та відмінні риси, необхідність вивчення. Різновиди гармонічних коливань, їх характерні властивості. Гармонічний осцилятор як диференційна система, різновиди, призначення.РЕФЕРАТ
на тему:” Механічні й електромагнітні коливання ”
План
1. Гармонічні коливання і їх характеристики
2. Механічні гармонічні коливання
3. Гармонічний осцилятор. Пружинний, фізичний і математичний маятники
4. Вільні гармонійні коливання в коливальному контурі
1. Гармонічні коливання і їх характеристики
Коливаннями називаються рухи або процеси, які характеризуються певною повторюваністю в часі. Коливальні процеси широко поширені в природі й техніці, наприклад, коливання маятника годинника, змінний електричний струм і т.д. При коливальному русі маятника змінюється координата його центра мас, у випадку змінного струму - коливаються напруга й струм у ланцюзі. Фізична природа коливань може бути різною, тому розрізняють коливання механічні, електромагнітні й ін. Однак різні коливальні процеси описуються однаковими характеристиками й однаковими рівняннями. Звідси випливає доцільність єдиного підходу до вивчення коливань різної фізичної природи.
Коливання будуть вільними (або власними), якщо вони відбуваються за рахунок деякої енергії, переданої коливальній системі в початковий момент часу, при відсутності в наступні моменти часу будь-яких зовнішніх впливів на цю систему. Найпростішими коливаннями є гармонічні коливання, при яких коливна величина змінюється з часом за законом косинуса або синуса. Вивчення гармонічних коливань важливе з двох причин:
1) коливання, які зустрічаються у природі й техніці, при певних наближеннях є гармонічними;
2) різні періодичні процеси (процеси, які повторюються через рівні проміжки часу), можна подавати як суперпозицію гармонічних коливань.
Гармонічні коливання деякої фізичної величини х описуються таким рівнянням
(1)
де А-
максимальне значення коливної величини x
, яке називається амплітудою коливань
; 
- колова, або циклічна частота; - початкова фаза коливань для моменту часу t =
0; 
- фаза коливань для довільного моменту часу t.
Так як косинус змінюється в межах від +1 до -1, то х
може набувати значень від +А
до -А.
Певні стани системи в процесі гармонічних коливань повторюються
через однаковий проміжок часу Т, який називається періодом коливань . За цей час фаза коливання зростає на 2, тобто
звідки
(2)
Величина, обернена до періоду коливань
(3)
виконана коливною системою за одиницю часу, називається частотою коливань. Прирівнюючи (2) і (3), одержимо
0
= 2
.
Одиницею частоти є герц (Гц), це частота такого періодичного процесу, при якому за 1 с відбувається одне повне коливання.
Запишемо першу й другу похідні фізичної величини х гармонічного коливання, тобто визначимо швидкість і прискорення коливання:
(4)
(5)
тобто маємо гармонічні коливання тієї ж циклічної частоти. Амплітуди величин (4) і (5) відповідно дорівнюють 
і 
. Фаза швидкості (4) відрізняється від фази фізичної величини (1) на /2, а фаза прискорення (5) відрізняється від фази фізичної величини (1) на .
Отже, у моменти часу, коли х =
0, 
має найбільші значення; коли ж x
досягає максимальних від’ємних значень то в ці моменти часу 
будуть мати найбільші додатні значення (рис. 1).
З рівняння (5) одержуємо диференціальне рівняння гармонічних коливань (де враховано, що х = A cos ( t + )),
. (6)
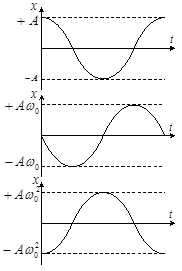
Рис. 1
Таким чином, розв’язком диференціального рівняння (6) є вираз (1).
Гармонічні коливання можна зобразити графічно за допомогою методу обертання вектора амплітуди, або методу векторних діаграм. Для цього з довільної точки О,
взятої на осі х,
під кутом , який дорівнює початковій фазі коливання, відкладається вектор 
, модуль якого дорівнює амплітуді А
гармонічного коливання (рис. 2).
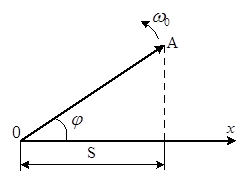
Рис. 2
Якщо цей вектор привести до обертання з кутовою швидкістю 
то проекція кінця вектора буде переміщуватися по осі x
і набувати значень від -А
до + А,
а коливна величина буде змінюватися з часом за законом х
= A
cos(
t + ). У фізиці часто застосовується інший метод, який відрізняється від методу обертання вектора амплітуди лише за формою. У цьому методі коливну величину подають комплексним числом. Відповідно до формули Ейлера, для комплексних чисел
(7)
де 
- уявна одиниця. Тому рівняння гармонічного коливання (1) можна записати також в експонентній формі так:
(8)
Права частина рівняння (8) є рівнянням гармонічних коливань.
2. Механічні гармонічні коливання
Нехай матеріальна точка виконує прямолінійні гармонічні коливання уздовж осі координат x біля положення рівноваги, прийнятого за початок координат. Тоді залежність координати x від часу t задається рівнянням (1),
(9)
Відповідно до виразів (4) і (5) швидкість 
і прискорення а
коливної точки будуть дорівнювати:
(10)
Сила F = ma , що діє на коливну матеріальну точку масою т, у відповідності з рівнянням (1) дорівнює
Отже сила, яка діє на матеріальну точку при гармонічних коливаннях, пропорційна зміщенню матеріальної точки від положення рівноваги і спрямована в протилежну сторону.
Кінетична енергія матеріальної точки, яка здійснює прямолінійні гармонійні коливання, дорівнює
(11)
або
К
=
(12)
Потенціальна енергія матеріальної точки, яка здійснює гармонічні коливання під дією пружної сили F, дорівнює
П
= -
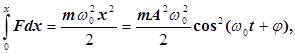(13)
або
П
=
(14)
Рис. 3
Додавши (13) і (14), одержимо формулу для повної енергії гармонічного коливання:
(15)
З формул (12) і (14) видно, що К і змінюються в часі з частотою, яка у два рази перевищує частоту гармонічного коливання. На рис. 3 показані графіки залежності х, К і від часу.
Оскільки середні значення 
то з формул (11), (13) і (15) випливає, що
3. Гармонічний осцилятор. Пружинний, фізичний і математичний маятники
Гармонічним осцилятором називається система, яка описується диференціальним рівнянням виду (6):
(16)
Коливання гармонічного осцилятора є важливим прикладом періодичного руху і служать точною або наближеною моделлю в багатьох задачах класичної і квантової фізики. Прикладами гармонічного осцилятора є пружинний, фізичний і математичний маятники, коливальний контур (для струмів і напруг настільки малих, щоб елементи контуру можна було вважати лінійними).
Пружинний маятник. Пружинний маятник – невеличке тіло масою т, яке підвішене до абсолютно пружної пружині і здійснює гармонічні коливання під дією пружної сили F = - kx , де k - коефіцієнт пружності, у випадку пружини, названий жорсткістю (рис. 4).
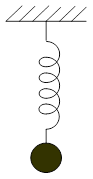
Рис.4
Диференціальне рівняння коливання маятника буде мати вигляд
або
(17)
З виразів (16) і (1) випливає, що пружинний маятник виконує гармонічні коливання за законом 
з циклічною частотою
і періодом 
Формула (17) справедлива для пружних коливань у межах, для яких виконується закон Гука, тобто коли маса пружини мала в порівнянні з масою тіла.
В цьому випадку потенціальна енергія пружинного маятника, згідно (13) дорівнює
(18)
Фізичний маятник. Фізичний маятник – тверде тіло, яке під дією сили тяжіння виконує гармонічні коливання відносно нерухомої горизонтальної осі або підвісу, що не збігається з центром мас С тіла (рис. 5).
Якщо маятник відхилений від положення рівноваги на деякий кут 
, то відповідно до основного рівняння динаміки обертального руху твердого тіла момент
сили F
, яка повертає маятник до положення рівноваги буде дорівнювати
(19)
де J
- момент інерції маятника відносно осі, яка проходить через точку О, l -
відстань між точкою підвісу і центром мас маятника, 
– сила, яка повертає маятник у попереднє положення, (знак мінус обумовлений тим, що зростання 
і швидкості 
завжди протилежні; sin
відповідає малим коливанням маятника, тобто малим відхиленням маятника від положення рівноваги.
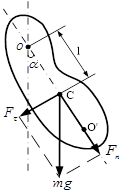
Рис. 5
Рівняння (19) можна записати у вигляді
або
Приймаючи, що 
одержимо рівняння 
ідентичне з (16), розв’язком якого є функція:
(20)
З виразу (20) випливає, що при малих коливаннях фізичний маятник виконує гармонічні коливання з циклічною частотою 
і періодом
(21)
де 
– приведена довжина фізичного маятника.
Точка 0 на продовженні прямої 0С, яка відстоїть від осі підвісу на відстані приведеної довжини L, називається центром коливань фізичного маятника (рис. 5). Застосовуючи теорему Штейнера, можна показати, що 00 завжди більше 0С = l. Точка підвісу 0 і центр коливань 0 мають властивість взаємозамінності, якщо вісь підвісу перенести в центр коливань, то точка 0, в якій розміщувалась раніше вісь підвісу стане новим центром коливань і період коливань фізичного маятника не зміниться.
Математичний маятник. Математичний маятник – ідеалізована система, яка складається з матеріальної точки масою т, підвішеної на нерозтяжній невагомій нитці, і коливається під дією сили тяжіння (рис.6).
Гарним наближенням математичного маятника є невелика важка кулька, підвішений на тонкій довгій нитці. Момент інерції математичного маятника дорівнює
(22)
де l - довжина маятника.
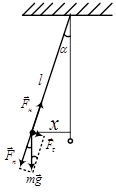
Рис. 6
Так як математичний маятник можна подати як окремий випадок фізичного маятника, припустивши, що вся маса фізичного маятника зосереджена в одній точці – центрі мас, то, підставивши вираз (22) у формулу (21), одержимо знайомий вираз для малих коливань математичного маятника:
(23)
Порівнюючи формули (23) і (21), бачимо, що якщо приведена довжина L фізичного маятника дорівнює довжині l математичного маятника, то їх періоди коливань збігаються. Отже, приведена довжина фізичного маятника – це довжина такого математичного маятника, період коливань якого збігається з періодом коливань даного фізичного маятника.
4. Вільні гармонійні коливання у коливальному контурі
Серед різних електричних явищ особливе місце займають електромагнітні коливання, при яких фізичні величини (заряди, струми, електричні і магнітні поля) періодично змінюються. Для виникнення і підтримування електромагнітних коливань необхідні певні системи, найпростішою з який є коливальний контур – ланцюг, який складається з увімкнених послідовно котушки індуктивністю L , конденсатора ємністю С і резистора опором R.
Розглянемо послідовні стадії коливального процесу в ідеалізованому контурі, опір якого безмежно малий 
Для виникнення в контурі коливань конденсатор попередньо заряджають, надаючи його обкладкам заряди 
Q.
Тоді в початковий момент часу 
(рис. 5, а) між обкладками конденсатора виникне електричне поле, енергія якого
Замкнувши конденсатор на котушку індуктивності, він почне розряджатися й у контурі потече зростаючий з часом струм I . У результаті енергія електричного поля буде зменшуватися, а енергія магнітного поля котушки – зростати.
Так як 
, то, відповідно до закону збереження енергії, повна енергія контуру буде дорівнювати
тому що енергія на нагрівання провідників у такому коливальному контурі не витрачається. У момент часу 
, коли конденсатор повністю розрядиться, енергія електричного поля зменшується до нуля, а енергія магнітного поля, а отже, і струм досягають найбільшого значення (рис. 5,б). Починаючи з цього моменту часу струм у контурі буде зменшуватися; отже, почне слабшати магнітне поле котушки й індукований у ній струм, який тече (відповідно до правила Ленца) у тому ж напрямку, що й струм розрядки конденсатора. Конденсатор почне перезаряджатися, при цьому виникне електричне поле, яке намагатиметься послабити струм, який зрештою зменшується до нуля, а заряд на обкладках конденсатора досягне максимуму (рис. 5, в). Далі ті ж процеси почнуть протікати в зворотному напрямку (рис. 5, г) і система до моменту часу t =
прийде в початковий стан (рис. 5, а). Після цього почнеться повторення розглянутого циклу розрядки і зарядки конденсатора.
Якби втрат енергії не було, то в контурі відбувалися б періодичні незатухаючі коливання, тобто періодично змінювалися (коливалися) б заряд Q на обкладках конденсатора, напруга U на конденсаторі і сила струму I , яка тече через котушку індуктивності.
Отже, у контурі виникають електричні коливання з періодом Т , причому протягом першої половини періоду струм тече в одному напрямку, протягом другої половини – у протилежному. Коливання супроводжуються перетвореннями енергій електричних і магнітних полів.
Електричні коливання у коливальному контурі можна зіставити з механічними коливаннями маятника (рис. 7), які супроводжуються взаємними перетвореннями потенціальної і кінетичної енергій маятника.
У даному випадку потенціальна енергія маятника 
аналогічна енергії електричного поля конденсатора 
, кінетична енергія маятника 
– енергії магнітного поля котушки 
, а швидкість руху маятника – силі струму в контурі.
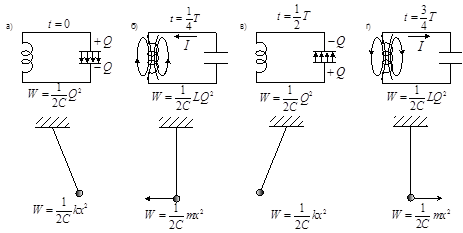
Рис.7
Роль інерції маятника буде зводитися до самоіндукції котушки, а роль сили тертя, яке діє на маятник – до опору контуру.
Відповідно до другого правила Кірхгофа, для контуру, який містить котушку індуктивністю L , конденсатор ємністю С и резистор опором R маємо
,
де IR –
спад напруги на резисторі, 
- напруга на конден-саторі, 
- е. р. с. самоіндукції, яка виникає в котушці при проті-канні в ній змінного струму (
- єдина е.р.с. у контурі).
Отже,
. (24)
Розділивши (24) на L і підставивши
і 
, одержимо диференціальне рівняння коливань заряду Q
у контурі:
(25)
У даному коливальному контурі зовнішні е. р. с. відсутні, тому розглянуті коливання є вільними коливаннями. Якщо опір R = 0, то вільні електромагнітні коливання у контурі є гармонічними. Тоді з (25) одержимо диференціальне рівняння вільних гармонічних коливань заряду Q в контурі:
(26)
З виразу (26) випливає, що заряд Q в коливальному контурі виконує гармонічні коливання за законом
(27)
де Qm — амплітуда коливань заряду конденсатора з циклічною частотою 0 , яка називається власною частотою контуру:
(28)
і періодом
(29)
Формула (29) вперше була отримана Томсоном і називається формулою Томсона.
Сила струму в коливальному контурі буде дорівнювати
(30)
де 
- амплітуда сили струму.
Напруга на конденсаторі
(31)
де 
— амплітуда напруги.
З виразів (30) і (31) випливає, що коливання струму I випереджають по фазі коливання заряду Q на /2, тобто коли струм досягає максимального значення, заряд (а також і напруга звертаються в нуль і навпаки. Цей взаємозвязок був установлений при розгляді послідовних стадій коливального процесу в контурі і на підставі енергетичних міркувань. Вільні електромагнітні коливання в контурі є незатухаючими.