Метод простых итераций с попеременно чередующимся шагом

СОДЕРЖАНИЕ: Учреждение образования «Брестский государственный университет имени А.С. Пушкина» Кафедра информатики и прикладной математики Курсовая работа Метод простых итераций с попеременно чередующимся шагом

Учреждение образования

«Брестский государственный университет имени А.С. Пушкина»

Кафедра информатики и прикладной математики

Курсовая работа

Метод простых итераций с попеременно чередующимся шагом

Брест 2010

Содержание

Априорный выбор числа итераций в методе простых итераций с попеременно чередующимся шагом для уравнений I рода

Постановка задачи

Сходимость при точной правой части

Сходимость при приближенной правой части

Оценка погрешности

Априорный выбор числа итераций в методе простых итераций с попеременно чередующимся шагом для уравнений I рода

Как известно, погрешность метода простых итераций с постоянным или переменным шагом зависит от суммы итерационных шагов и притом так, что для сокращения числа итераций желательно, чтобы итерационные шаги были как можно большими. Однако на эти шаги накладываются ограничения сверху. Возникает идея попытаться ослабить эти ограничения. Это удаётся сделать, выбирая для шага два значения и попеременно, где уже не обязано удовлетворять прежним требованиям.

Постановка задачи

В гильбертовом пространстве решается уравнение I рода с положительным ограниченным самосопряжённым оператором , для которого нуль не является собственным значением. Используется итерационный метод

(4.1)

Предполагая существование единственного точного решения уравнения при точной правой части , ищем его приближение при приближенной правой части . В этом случае метод примет вид

(4.2)

Сходимость при точной правой части

Считаем . Тогда, воспользовавшись интегральным представлением самосопряжённого оператора, получим

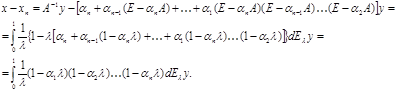
Так как

Поэтому

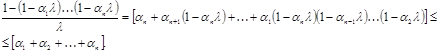
Если , то

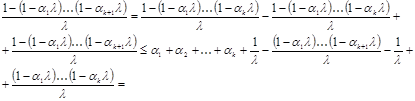
при ,

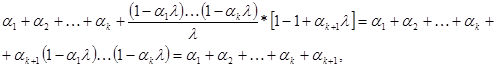
То

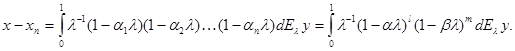
Здесь натуральные показатели, или . Потребуем, чтобы здесь и всюду ниже для , удовлетворяющих условию , для было

(4.3)

для любого , т.е. . Правое неравенство даёт . Так как , то

(4.4)

Левое неравенство даёт

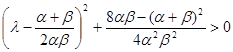Отсюда ,

(4.5)

Из (4.4) и (4.5), двигаясь в обратном порядке, легко получить (4.3). Следовательно, условие (4.3) равносильно совокупности условий (4.4) и (4.5). Из (4.4) и (4.5) получаем следствие:

(4.6)

Докажем сходимость процесса (4.1) при точной правой части. Справедлива следующая теорема.

Теорема: Итерационный процесс (4.1) при условиях , и (4.3) сходится в исходной норме гильбертова пространства.

Доказательство:

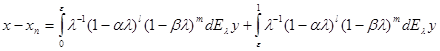При условиях , и (4.3) второй интеграл сходится, так как

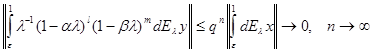Здесь .

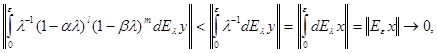
так как сильно стремится к нулю при . Таким образом, . Теорема доказана.

Сходимость при приближенной правой части

Докажем сходимость процесса (4.2) при приближенной правой части уравнения . Справедлива следующая теорема.

Теорема: При условиях , и (4.3) итерационный процесс (4.2) сходится, если выбирать число итераций из условия .

Доказательство: Рассмотрим

Оценим , где

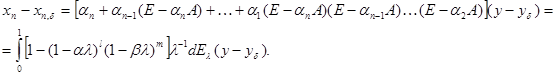
Найдём на максимум подынтегральной функции

Так как

Если , то

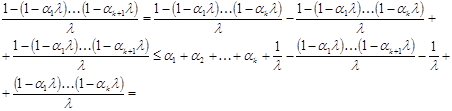
при ,

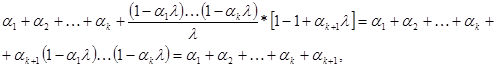
поэтому. Отсюда получим . Поскольку и , то для сходимости метода (4.2) достаточно потребовать, чтобы . Таким образом, достаточно, чтобы . Теорема доказана.

Оценка погрешности

Для оценки скорости сходимости предположим истокопредставимость точного решения, т.е. . Тогда

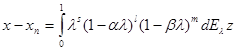Для упрощения будем считать число чётным, т.е. и найдём оценку для . С этой целью оценим модуль подынтегральной функции

. Первый сомножитель для . Второй сомножитель для малых близок к единице, т.е. тоже положителен. Поэтому по крайней мере для всех , не превосходящих первой стационарной точки. Найдём стационарные точки функции .

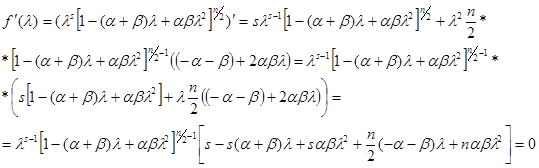Первые два сомножителя не равны нулю, в противном случае . Следовательно, полное квадратное уравнение. Отсюда получим, что

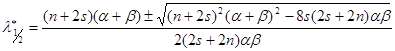
стационарные точки функции . Рассмотрим :

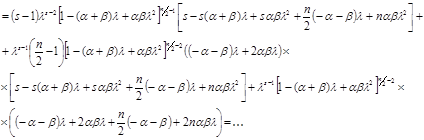
где

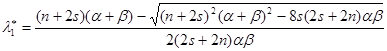Имеем

так как первые два сомножителя при условии (4.3) положительны. Значит, точка максимума функции . Оценим в точке .

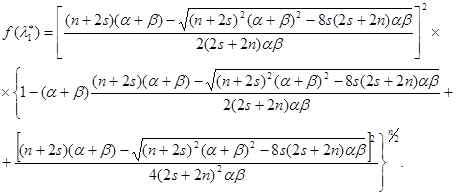
Покажем, что

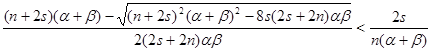. (4.7)

Предположим, что (4.7) справедливо. Оно равносильно неравенству

которое, в свою очередь, равносильно такому

(4.8)

Возведение в квадрат обеих частей неравенства (4.8) даст эквивалентное неравенство, если левая часть неотрицательна. Установим, при каких это будет.

Очевидно, при , .

Будем считать и возведём обе части неравенства (4.8) в квадрат. После приведения подобных членов получим

или

т.е..

При последнее неравенство справедливо и, следовательно, в силу равносильности неравенств, справедливо неравенство (4.7). Отсюда

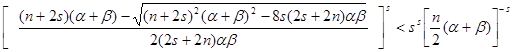Оценим теперь . Покажем, что

, (4.9)

т.е. , т.е.

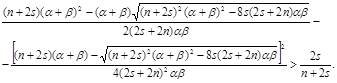
Преобразовав последнее неравенство, получим

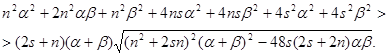
После возведения обеих частей неравенства в квадрат и приведения подобных членов, получим очевидное неравенство

В силу равносильности неравенств справедливо неравенство (4.9), так что

Таким образом, для справедлива оценка

Оценим в точке

Сначала потребуем, чтобы , т.е.

Усилим неравенство

Отсюда . При , причём, при .Пусть , тогда при условии

(4.10)

имеем , т.е. . В противном случае , и оно нас не интересует. Оценим при условии (4.10) функцию .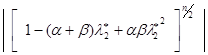

Для этого сначала оценим , так как в точке функция . Найдем, при каких условиях выполняется неравенство

(4.11)

Подставив в (4.11), получим

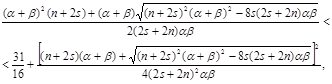
что после упрощения даёт

Возведём обе части неравенства в квадрат, получим

1 случай:

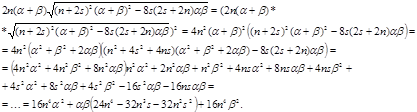
2 случай:

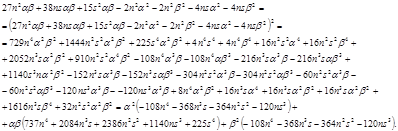
Следовательно:

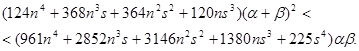
Очевидно, что при условии (4.5) это неравенство справедливо и, следовательно, справедливо (4.11). Итак, при условиях (4.5) и (4.10) справедлива оценка

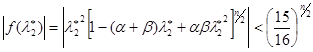На концах отрезка имеем . Таким образом, получим следующие оценки для :

1. в точке ;

2. в точке при условии (4.5) и (4.11) ;

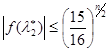3. в точке .

Найдём условия, при которых , т.е. . Это равносильно условию

. (4.12)

Таким образом, если выбирать и из условия (4.12), то .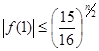

Поскольку геометрическая прогрессия убывает быстрее, чем , то 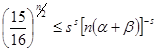для достаточно больших . Поэтому для таких справедлива оценка .

Так как , то при условиях , (4.4), (4.5), (4.10) и (4.12) имеет место следующая оценка погрешности итерационного метода (4.2)

. (4.13)

Нетрудно видеть, что условие (4.12) сильнее условия (4.4). Для нахождения оптимальной по оценки погрешности производную по от правой части выражения (4.13) приравняем к нулю. Тогда оптимальная по оценка погрешности имеет вид

(4.14)

и получается при

. (4.15)

Итак, доказана

Теорема: При условиях , , , (4.10), (4.5), (4.12) оценка погрешности метода (4.2) имеет вид (4.13) при достаточно больших . При этих же условиях оптимальная оценка имеет вид(4.14) и получается при из (4.15).

Таким образом, оптимальная оценка метода (4.2) при неточности в правой части уравнения оказывается такой же, как и оценка для метода простых итераций. Как видно, метод (4.2) не дает преимущества в мажорантных оценках по сравнению с методом простых итераций. Но он дает выигрыш в следующем. В методе простых итераций с постоянным шагом (2) требуется условие , в этом же методе с переменным шагом допускается более широкий диапазон для больших . В методе (4.2) . Следовательно, выбирая и соответствующим образом, можно считать в методе (4.2) примерно втрое меньшим, чем для метода простых итераций с постоянным шагом, и вдвое меньшим, чем для того метода с переменным шагом. Таким образом, используя метод (4.2), для достижения оптимальной точности достаточно сделать итераций соответственно в три раза или два раза меньше. Приведем несколько подходящих значений , удовлетворяющих требуемым условиям:

	0,8	0,9	1,0	1,1	1,15	1,17	1,3
	4,4	5,0	5,5	6,1	6,4	6,5	4,1

Наибольшую сумму и, следовательно, наибольший выигрыш в объеме вычислений дают значения и . Поскольку в выделенном случае , то условие (4.6) показывает, что достигнут практически максимальный возможный выигрыш.

Замечание: Оценки сходимости были получены для случая, когда . В случае, когда , во всех оценках следует заменить на .

Замечание: Считаем, что . На самом деле все результаты легко переносятся на случай, когда .

Литература

1. В.Ф. Савчук, О.В. Матысик «Регуляризация операторных уравнений в гильбертовом пространстве», Брест, 2008, 195 стр.

Скачать архив с текстом документа