Методика изучения динамики твердого тела в курсе физики профильной средней школы
СОДЕРЖАНИЕ: Поиск эффективных методов преподавания теории вращательного движения в профильных классах с углубленным изучением физики. Изучение движения материальной точки по окружности. Понятие динамики вращательного движения твердого тела вокруг неподвижной оси.Содержание
Введение
Методика изучения вращательное движение твердого тела в классах с углубленным изучением физики
Конспект урока по теме «Вращательное движение тел»
Примеры решения задач по теме «Динамика вращательного движения твердого тела вокруг неподвижной оси»
Задача №1
Задача №2
Задача №3
Список используемой литературы
Введение
Одной из главных особенностей современного периода реформирования школьного образования является ориентация школьного образования на широкую дифференциацию обучения, позволяющую удовлетворить потребности каждого учащегося, в том числе и тех, кто проявляет особый интерес и способности к предмету.
В настоящий момент эта тенденция углубляется переходом старшей ступени средней школы на профильное обучение, что позволяет обеспечить восстановление преемственности среднего и высшего образования. Концепция профильного обучения определила его целью «повышение качества образования и установление равного доступа к полноценному образованию различных категорий учащихся в соответствии с их индивидуальными склонностями и потребностями».
Для учащихся это означает, что выбор физико-математического профиля обучения должен гарантировать такой уровень обучения, который бы позволял удовлетворить главную потребность данной группы учащихся -продолжение обучения в высших учебных заведениях соответствующего профиля. Выпускник средней школы, решивший продолжить образование в вузах физического и технического профилей должен иметь углубленную подготовку по физике. Она является необходимой базой обучения в этих вузах.
Решение задач профильного обучения физике возможно только при условии использования расширенных, углубленных программ. Анализ содержания программ для профильных классов различных авторских коллективов показывает, что все они содержат расширенный, по сравнению с базовыми программами, объем учебного материала по всем разделам физики и предусматривают его углубленное изучение. Составной частью содержания раздела «Механика» этих программ является теория вращательного движения.
При изучении кинематики вращательного движения формируются понятия угловых характеристик (угловое перемещение, угловая скорость, угловое ускорение), показывается их связь друг с другом и с линейными характеристиками движения. При изучении динамики вращательного движения формируются понятия «момент инерции», «момент импульса», происходит углубление понятия «момент силы». Особую важность представляют изучение основного закона динамики вращательного движения, закона сохранения момента импульса, теоремы Гюйгенса-Штейнера о вычислении момента инерции при переносе оси вращения, вычисление кинетической энергии вращающегося тела.
Знания кинематических и динамических характеристик и законов вращательного движения необходимы для углубленного изучения не только механики, но и других разделов физики. Теория вращательного движения, предполагающая на первый взгляд, «узкую» область использования, имеет большое значение для последующего изучения небесной механики, теории колебаний физического маятника, теорий теплоемкости веществ и поляризации диэлектриков, движения заряженных частиц в магнитном поле, магнитных свойств веществ, классической и квантовой моделей атома.
Анализ содержания заданий, предлагаемых абитуриентам на вступительных экзаменах по физике в ведущих физико-технических вузах страны, также показывает, что знания по теории вращательного движения способствуют успешному выполнению таких заданий.
Существующий уровень профессионально-методической подготовленности большинства учителей физики к преподаванию теории вращательного движения в условиях профильного обучения недостаточен, у многих учителей нет полного понимания роли теории вращательного движения в изучении школьного курса физики. Поэтому необходима более глубокая профессионально-методическая подготовка, которая позволила бы учителю максимально использовать дидактические возможности для решения задач профильного обучения.
Отсутствие в действующих программах педвузов по теории и методике преподавания физики раздела «Научно-методический анализ и методика изучения теории вращательного движения» приводит к тому, что выпускники педвузов также оказываются недостаточно подготовленными к решению стоящих перед ними профессиональных задач в процессе преподавания теории вращательного движения в профильных классах.
Таким образом, актуальность исследования определяется: противоречием между требованиями, предъявляемыми школьными профильными программами для углубленного изучения физики к уровню знаний учащихся по теории вращательного движения и реальным уровнем знаний учащихся; противоречием между задачами, стоящими перед учителем в процессе преподавания теории вращательного движения в классах с углубленным изучением физики, и уровнем его соответствующей профессионально-методической подготовки.
Проблемой исследования является поиск эффективных методов преподавания теории вращательного движения в профильных классах с углубленным изучением физики.
Цель исследования состоит в разработке эффективных методов преподавания теории вращательного движения, способствующих повышению уровня знаний учащихся, необходимых для глубокого усвоения школьного курса физики, и содержания соответствующей профессионально-методической подготовки учителя.
Объектом исследования являются процесс обучения физике учащихся классов с углубленным изучением предмета.
Предметом исследования является методика преподавания теории вращательного движения и других разделов в классах с углубленным изучением физики.
Гипотеза исследования: Если разработать методику преподавания кинематики и динамики вращательного движения, то это позволит повысить уровень знаний учащихся не только по теории вращательного движения, но и по другим разделам школьного курса физики, где используются элементы этой теории.
вращательный движение физика тело
Методика изучения вращательное движение твердого тела в классах с углубленным изучением физики
Изучение динамики вращательного движения твердого тела преследует следующую цель: познакомить учащихся с законами движения тел под действием моментов приложенных к ним сил. Для этого необходимо ввести понятие момента силы, момента импульса, момента инерции, изучить закон сохранения момента импульса относительно неподвижной оси.
Изучение вращательного движения твердого тела целесообразно начать с изучения движения материальной точки по окружности. В этом случае легко ввести понятие момента сил относительно оси вращения и получить уравнение вращательного движения. Необходимо заметить, что эта тема является трудной для усвоения, поэтому для лучшего понимания и запоминания главных соотношений рекомендуется проводить сопоставления с формулами для поступательного движения. Учащимся известно, что динамика поступательного движения изучает причины возникновения ускорения тел и позволяет вычислить их направления и величину. Второй закон Ньютона устанавливает зависимость величины и направления ускорения от действующей силы и массы тела. Динамика вращательного движения изучает причины появления углового ускорения. Основное уравнение вращательного движения устанавливает зависимость углового ускорения от момента силы и момента инерции тела.
Далее, рассматривая твердое тело как систему материальных точек, вращающихся по окружности, центры которых лежат на оси вращения твердого тела, легко получить уравнение движения абсолютно твердого тела вокруг неподвижной оси. Трудность решения уравнения состоит в необходимости вычисления момента инерции тела относительно его оси вращения. Если нет возможности ознакомить учащихся с методами вычисления моментов инерции, например, из-за их недостаточной математической подготовки, то можно без вывода дать значения моментов инерции таких тел как шар, диск. Как показывает опыт, учащиеся с трудом усваивают понятие о векторном характере угловой скорости, момента силы и момента импульса. Поэтому необходимо выделить возможно большее время для изучения этого раздела, рассмотреть большее число примеров и задач (или делать это на внеклассных занятиях).
Продолжая аналогию с поступательным движением, рассмотрите закон сохранения момента импульса. При изучении динамики поступательного движения отмечалось, что в результате действия силы изменяется импульс тела. При вращательном движении изменяется момент импульса под действием момента силы. Если момент внешних сил равен нулю, то момент импульса сохраняется.
Ранее отмечалось, что внутренние силы не могут изменять скорость поступательного движения центра масс системы тел. Если же под действием внутренних сил изменить расположение отдельных частей вращающегося тела, то сохраняется общий момент импульса, а угловая скорость системы изменяется.
 |
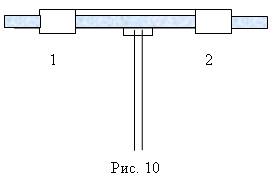Для демонстрации этого эффекта можно воспользоваться установкой, в которой две шайбы надеваются на стержень, скрепленный с центробежной машиной. Шайбы соединены нитью (рис. 10). Вся система вращается с некоторой угловой скоростью. Когда нить пережигают, грузы разбегаются, момент инерции увеличивается, а угловая скорость уменьшается.
Пример решения задачи на закон сохранения момента импульса. Горизонтальная платформа массой M и радиусом R вращается с угловой скоростью. На краю платформы стоит человек массой m. С какой угловой скоростью будет вращаться платформа, если человек перейдет от края платформы к ее центру? Человека можно рассматривать как материальную точку.
Решение. Сумма моментов всех внешних сил относительно оси вращения равна нулю, поэтому можно применить закон сохранения момента импульса.
 |
Момент инерции платформы
момент инерции человека
 |
Первоначально сумма моментов импульса человека и платформы была
Конечная сумма моментов импульса
Из закона сохранения момента импульса следует:
Решая уравнение относительно омега 1 , получим
Конспект урока по теме «Вращательное движение тел»
Тип урока: Интерактивная лекция, 2 ч.
Цели урока:
Социально – психологическая:
Обучающиеся должны выявлять собственный уровень понимания и усвоения основных понятий кинематики и динамики вращательного движения, основного уравнения динамики вращательного движения, закона сохранения момента импульса, методов расчёта кинетической энергии вращения; критически относиться к собственным достижениям в умении применять основное уравнение динамики вращательного движения и закон сохранения момента импульса к решению физических задач; развивать свои коммуникативные способности: принимать участие в обсуждении поставленной на уроке проблемы; выслушивать мнение своих товарищей; способствовать сотрудничеству в парах, группах при выполнении практических заданий и т.д.
Академическая:
Обучающиеся должны усвоить , что величина углового ускорения тела при вращательном движении зависит от суммарного момента приложенных сил и момента инерции тела, что момент инерции – скалярная физическая величина, характеризующая распределение масс в системе, и научиться определять момент инерции симметричных тел относительно произвольных осей, пользуясь теоремой Штейнера. Знать, что момент импульса - величина векторная, сохраняющая численное значение и направление в пространстве при равенстве нулю суммарного момента внешних сил, действующих на тело или замкнутую систему тел (закон сохранения момента импульса), понимать, что закон сохранения момента импульса является фундаментальным законом природы, следствием изотропности пространства. Уметь определять направление угловой скорости, углового ускорения, момента сил и момента импульса, пользуясь правилом правого винта.
Знать математические выражения основного уравнения динамики вращательного движения, закона сохранения момента импульса, формул для определения численного значения момента импульса и кинетической энергии вращающегося тела и уметь ими пользоваться при решении разного рода практических задач. Знать единицы измерения момента импульса, момента инерции.
Понимать , что между вращательным движением твёрдого тела вокруг неподвижной оси и движением материальной точки по окружности (или поступательным движением тела, которое можно рассматривать как движение по окружности бесконечно большого радиуса) существует неформальная аналогия, в которой проявляется материальное единство мира.
Задачи урока:
Образовательные:
Продолжить формирование новых компетенций, знаний и умений, способов деятельности, которые потребуются обучающимся в новой информационной среде обитания, путём использования современных информационных технологий обучения.
Способствовать формированию целостного миропонимания, путём использования метода аналогий, сравнивая вращательное движение твёрдого тела с поступательным движением, а также вращательное движение твёрдого тела с движением материальной точки по окружности, рассматривая вращательное движение твёрдого тела единым блоком: кинематическое описание движения, основное уравнение динамики вращательного движения, закон сохранения момента импульса как следствие изотропности пространства и его проявления на практике, расчёт кинетической энергии вращающегося твёрдого тела и применение закона сохранения энергии к вращающимся телам.
Показать возможности высокоразвитой информационной среды – Интернета – в деле получения образования.
Воспитательные:
Продолжить формирование мировоззренческой идеи познаваемости явлений и свойств материального мира. Научить учащихся выявлять причинно-следственные связи при изучении закономерностей вращательного движения твёрдого тела, раскрыть значение сведений о вращательном движении для науки и техники.
Содействовать дальнейшему формированию у обучающихся положительных мотивов учения.
Развивающие:
Продолжить формирование ключевых компетенций, в том числе информационно-коммуникативной компетентности обучающихся: умения самостоятельно искать и отбирать нужную информацию, анализировать, организовывать, представлять, передавать её, моделировать объекты и процессы.
Содействовать развитию мышления учащихся, активизации познавательной деятельности путём использования частично-поискового метода при решении проблемной ситуации.
Продолжить развитие коммуникативных качеств личности путем использования парной работы над заданиями по компьютерному моделированию.
Способствовать сотрудничеству в микрогруппах, обеспечить условия как для самостоятельного получения значимой для всей группы информации, так и для выработки общего вывода из предложенного задания.
Необходимое оборудование и материалы: Интерактивная мультимедийная система:
· мультимедиа-проектор (проекционное устройство)
· интерактивная доска
· персональный компьютер
Компьютерный класс
Демонстрационное оборудование: Диск вращающийся с набором принадлежностей, маятник Максвелла, легко вращающийся стул в качестве «скамьи» Жуковского, гантели, детские игрушки: волчок (юла), деревянная пирамидка, игрушечные автомобили с инерционным механизмом.
Мотивация учащихся: Содействовать повышению мотивации обучения, эффективному формированию качественных знаний, умений и навыков учащихся посредством:
- создания и решения проблемной ситуации;
- представления учебного материала в интересной, визуализированной, интерактивной и максимально понятной для обучающихся форме (стратегическая цель конкурса – стратегическая цель урока).
Ход и содержание урока:
I. Создание проблемной ситуации.
Демонстрация: быстро вращающийся волчок (или юла) не падает, а попытки отклонить его от вертикали вызывают прецессию, но не падение. Волчок (дрейдл, тромпо – у разных народов разные названия) - незамысловатая с виду игрушка с необычными свойствами!
«Поведение волчка в высшей степени удивительно! Если он не вертится, то сразу опрокидывается, и его не удержать в равновесии на кончике. Но это совершенно другой предмет, когда он кружится: он не только не падает, но и проявляет сопротивление, когда его толкают, и даже принимает всё более и более вертикальное положение» - так говорил о волчке известный английский учёный Дж. Перри.
Почему не падает вращающийся волчок? Почему так «загадочно» реагирует на внешние воздействия? Почему, спустя некоторое время, ось волчка самопроизвольно спиралеобразно удаляется от вертикали, и волчок падает? Встречали ли вы подобное поведение объектов в природе или технике?
II. Изучение нового материала. Интерактивная лекция «Вращательное движение твёрдого тела».
1. Вводная часть лекции: распространённость вращательного движения в природе и технике (слайд 2).
2. Работа с информационным блоком 1 «Кинематика движения твёрдого тела по окружности» (слайды 3-9). Этапы деятельности:
2.1. Актуализация знаний: просмотр презентации «Кинематика вращательного движения материальной точки» - творческой работы Катасоновой Натальи к уроку «Кинематика движения материальной точки» Добавлена в основную презентацию, переход по гиперссылке (слайды 56-70).
2.2. Просмотр слайдов «Кинематика вращательного движения твёрдого тела», выявление аналогии в способах описания вращательного движения твёрдого тела и материальной точки (слайды 4-8).
2.3. Аннотация материалов для дополнительного изучения по вопросу «Кинематика вращательного движения твёрдого тела» в научно-популярном физико-математическом журнале «Квант» с помощью сети Интернет: открыть некоторые гиперссылки, прокомментировать содержательную часть статей и заданий к ним (слайд 9).
3. Работа с информационным блоком 2 «Динамика вращательного движения твёрдого тела» (слайды 10-21). Этапы деятельности:
3.1. Формулирование основной задачи динамики вращательного движения, выдвижение гипотезы о зависимости углового ускорения от массы вращающегося тела и действующих на тело сил на основе метода аналогии (слайд 11).
3.2. Экспериментальная проверка выдвинутой гипотезы с помощью прибора «Диск вращающийся с набором принадлежностей», формулирование выводов из опыта (фоновый слайд 12). Схема проведения опыта:
Исследование зависимости углового ускорения от момента действующих сил: а) от действующей силы F, когда плечо силы относительно оси вращения d диска остаётся постоянным (d = const);
б) от плеча силы относительно оси вращения при постоянной действующей силе (F = const);
в) от суммы моментов всех действующих на тело сил относительно данной оси вращения.
Исследование зависимости углового ускорения от свойств вращающегося тела: а) от массы вращающегося тела при неизменном моменте сил;
б) от распределения массы относительно оси вращения при неизменном моменте сил.
3.3. Вывод основного уравнения динамики вращательного движения на основе применения представления о твёрдом теле как совокупности материальных точек, движение каждой из которых можно описать вторым законом Ньютона; введения понятия момента инерции тела как скалярной физической величины, характеризующей распределение массы относительно оси вращения (слайды 13-14).
3.4. Компьютерный лабораторный эксперимент с моделью «Момент инерции» (слайд 15).
Цель эксперимента: убедиться в зависимости момента инерции системы тел от положения шаров на спице и положения оси вращения, которая может проходить как через центр спицы, так и через её концы.
3.5. Анализ способов расчёта моментов инерции твёрдых тел относительно разных осей. Работа с таблицей «Моменты инерции некоторых тел» (для симметричных тел относительно оси, проходящей через центр масс тела). Теорема Штейнера для вычисления момента инерции относительно произвольной оси (слайды 16-17).
3.6. Закрепление изученного материала. Решение задач о качении симметричных тел по наклонной плоскости на основе применения основного уравнения динамики вращательного движения и на сравнение движений скатывающегося и скользящего с наклонной плоскости твёрдых тел. Организация работы: работа в малых группах с проверкой решения задач с помощью интерактивной доски. (В презентации имеется слайд с решением задачи о качении шара и сплошного цилиндра с наклонной плоскости с общим выводом о зависимости ускорения центра масс, а, значит, и его скорости в конце наклонной плоскости от момента инерции тела) (слайды 18-21).
4. Работа с информационным блоком 3 «Закон сохранения момента импульса» (слайды 22-42). Этапы деятельности.
4.1. Введение понятия момента импульса как векторной характеристики вращающегося твёрдого тела по аналогии с импульсом поступательно движущегося тела. Формула для вычисления, единица измерения (слайд 23).
4.2. Закон сохранения момента импульса как важнейший закон природы: вывод математической записи закона из основного уравнения динамики вращательного движения, разъяснение, почему закон сохранения момента импульса следует считать фундаментальным законом природы наряду с законами сохранения линейного импульса и энергии. Анализ различий в применении закона сохранения импульса и закона сохранения момента импульса, имеющих сходную алгебраическую форму записи, к одному телу (слайды 24-25).
4.3. Демонстрация сохранения момента импульса с легко вращающимся стулом (аналогом скамьи Жуковского) и деревянной пирамидкой. Анализ опытов со скамьёй Жуковского (слайды 26-29) и опытов по неупругому вращательному столкновению двух дисков, насажанных на общую ось (слайд 30).
4.4. Учёт и использование закона сохранения момента импульса на практике. Анализ примеров (слайды 31-40).
4.5. Второй закон Кеплера как частный случай закона сохранения момента импульса (слайды 41-42).
Виртуальный эксперимент с моделью «Законы Кеплера».
Цель эксперимента: проиллюстрировать второй закон Кеплера на примере движения спутников Земли, меняя параметры их движения.
5. Работа с информационным блоком 4 «Кинетическая энергия вращающегося тела» (слайды 43-49). Этапы деятельности.
5.1. Вывод формулы кинетической энергии вращающегося тела. Кинетическая энергия твёрдого тела в плоском движении (слайды 44-46).
5.2. Применение закона сохранения механической энергии к вращательному движению (слайд 47).
5.3. Использование кинетической энергии вращательного движения на практике (слайды 48-49).
6. Заключение (слайды 50-53).
Аналогия как метод познания окружающего мира: физические системы или явления могут быть аналогичны как по своему поведению, так и по их математическому описанию. Часто при изучении других разделов физики можно найти механические аналогии процессов и явлений, но иногда можно найти немеханическую аналогию механическим процессам. Методом аналогии решаются задачи, выводятся уравнения. Метод аналогий не только способствует более глубокому пониманию учебного материала из разных разделов физики, но и свидетельствует о единстве материального мира.
Проверка и оценивание знаний, умений и навыков: Нет
Рефлексия деятельности на уроке:
Саморефлексия деятельности, процесса усвоения и психологического состояния на уроке в процессе работы над отдельными частями лекции.
Работа с рефлексивным экраном в конце урока (слайд 54) (выскажитесь одним предложением). Продолжите мысль:
- сегодня я узнал…
- было интересно…
- было трудно…
- я выполнял задания…
- учебные проблемы…
Домашнее задание
§ 6, 9, 10 (часть). Анализ примеров решения задач к § 6, 9. Творческое задание: подготовить по наиболее заинтересовавшему информационному блоку презентацию, интерактивный плакат или другой мультимедиа продукт. Вариант: тест или видеозадачник.
Дополнительная необходимая информация
Для подборки заданий использовать:
- Уокер Дж. Физический фейерверк. М.: Мир, 1988.
- Ресурсы Интернет.
Обоснование, почему данную тему оптимально изучать с использованием медиа-, мультимедиа, каким образом осуществить:
Учебный материал представлен в интересной, визуализированной, интерактивной и максимально понятной для обучающихся форме. Предусмотрен компьютерный эксперимент, выполняемый с интерактивными моделями (Открытая физика. 2.6), и решение задач с последующей проверкой с помощью интерактивной доски InterWrite. Имеется система подсказок-гиперссылок, помогающих решению задач. Презентация содержит гиперссылки на отдельные ресурсы Интернета (например, статьи электронной версии журнала «Квант»), которые можно просмотреть в режиме on-line, а также использовать для подготовки творческого задания. Для актуализации знаний служит подготовленная при изучении кинематики движения материальной точки презентация «Кинематика вращательного движения материальной точки».
Осуществляется компетентностный подход к организации учебного процесса, обеспечивается высокая мотивация учебной деятельности.
Советы по логическому переходу от данного урока к последующим:
В рамках блочно-зачётной системы с использованием методики укрупнения дидактических единиц усвоения данный урок является первым; предусмотрены уроки коррекции, закрепления знаний и зачётный урок с использованием дифференцированного по уровню сложности тестового задания. В зависимости от качества выполнения домашнего творческого задания возможно проведение в рамках изучения блока «Вращательное движение твёрдого тела»
Для закрепления знаний в классах с углубленный изучением физики при проведении практикума в конце года можно предложить следующую лабораторную работу «Изучение законов вращательного движения твердого тела на крестообразном маятнике Обербека»
1. Введение
Явления природы очень сложны. Даже такое обычное явление как движение тела, на самом деле оказывается совсем не простым. Чтобы понять главное и физическом явлении, не отвлекаясь на второстепенные летали, физики прибегают к моделированию, т.е. к выбору или построению упрощенной схемы явления. Вместо реального явления (или тела) изучают более простое фиктивное (несуществующее) явление, похожее на действительное в главных чертах. Такое фиктивное явление (тело) называют моделью.
Одной из важнейших моделей, с которой имеют дело в механике, является абсолютно твердое тело. В природе нет недеформируемых тел. Всякое тело пол действием приложенных к нему сил деформируется в большей или меньшей степени. Однако, в тех случаях, когда деформация тела мала и не влияет на его движение, рассматривают модель, называемую абсолютно твердым телом. Можно сказать, что абсолютно твердое тело - это система материальных точек, расстояние между которыми остается неизменным во время движения.
Одним из простых видов движения твердого тела является его вращение относительно неподвижной оси. Изучению законов вращательного движения твердого тела и посвящена настоящая лабораторная работа.
Напомним, что вращениетвердого тела вокруг неподвижной оси описывается уравнением моментов
(1)
Здесь 
- момент инерции тела относительно оси вращения, 
- угловая скорость вращения. Mx- сумма проекций моментов внешних сил на ось вращения OZ
.
Это уравнение по виду напоминает уравнение второго закона Ньютона:
.
Роль массы т играет момент инерции T, роль ускорения 
играет угловое ускорение 
, а роль силы 
играет момент сил Mx.
Уравнение (1) является прямым следствием законов Ньютона, поэтому его экспериментальная проверка является в то же время проверкой основных положений механики.
Как уже отмечалось, в работе изучается динамика вращательного движения твердого тела. В частности, экспериментально проверяется уравнение(1) - уравнение моментов для вращения твердого тела вокруг неподвижной оси.
2. Экспериментальная установка. Методика эксперимента.
Экспериментальная установка, схема которой представлена на рис.1, известна как маятник Обербека. Хотя на маятник эта установкасовсем непохожа, мы по традиции и для краткости будем называть ее маятником.
Маятник Обербека состоит из четырех спиц, укрепленных на втулке под прямым углом друг к другу. На той же втулке имеется шкив радиусом r . Вся эта система может свободно вращаться вокруг горизонтальной оси. Момент инерции системы можно менять, передвигая грузы то вдоль спиц.
 |
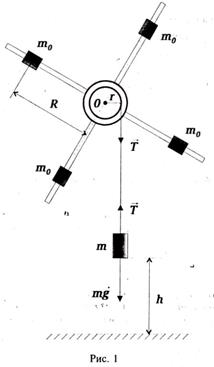Вращающий момент, создаваемый силой натяжения нитиT , равен Мн=Т r . Кроме того на маятник действуетмомент сил трения в оси – М mp - С учетом этого уравнение (1) примет вид
(2)
Согласно второму закону Ньютона для движения груза т имеем
ma=mg-T, (3)
где ускорение a
поступательного движения груза связано с угловым ускорением 
маятника кинематическим условием выражающим разматывание нити со шкива без проскальзывания. Решая уравнения (2)-(4) совместно, нетрудно получить угловое ускорение
(4)
(5)
Угловое ускорение, с другой стороны, можно довольно просто определить экспериментально. Действительно, измеряя время (, в течении которого груз т
опускается на расстояние h, можно найти ускорение а: a =2 h / t 2 , и, следовательно,
угловое ускорение
(6)
Формула (5) дает связь между величиной углового ускорения
,
которую можно измерить, и величиной момента инерции . В формулу (5) входит неизвестная величина М
mp
. Хотя момент сил трения мал, тем не менее он мал не на столько, чтобы им в уравнении (5) можно было пренебречь. Уменьшить относительную роль момента сил трения при данной конфигурации установки можно было бы, увеличивая массу груза m. Однако, здесь приходится принимать во внимание два обстоятельства:
1) увеличение массы т ведет к увеличениюдавления маятника на ось, что в свою очередь вызывает возрастание сил трения;
2) с увеличениемmуменьшается время движения (и снижается точность измерения времени, а значит ухудшается точность измерения величины углового ускорения.
Моментинерции, входящий в выражение (5), согласно теореме Гюйгенса-Штейнера и свойства аддитивности момента инерции может быть записан в виде
(7)
Здесь 
- момент инерции маятника, при условии, что центр масс каждого грузаm
0
находится на оси вращения. R - расстояние от оси до центров грузов то.
В уравнение (5) также входит величина т
r
2.
В
условиях опыта 
. (убедитесь в этом!).
Пренебрегая этой величиной в знаменателе (5), получаем простую формулу, которую можно проверить экспериментально
(8)
Экспериментально исследуем две зависимости:
1. Зависимость углового ускорения Е от момента внешней силы М=т
gr
при условии, что момент инерции остается постоянным. Если построить график зависимости =
f
(
M
)
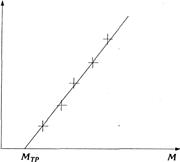
, то согласно (8) экспериментальные точки должны ложиться на прямую (рис.2), угловой коэффициент которой равен 
, а точка пересечения с осью ОМ
дает Мmp.
2.
|
|
2. Зависимость момента инерции - от расстояния Rгрузов до оси вращения маятника (соотношение (7)).
Выясним, как проверить эту зависимость экспериментально. Для этого преобразуем соотношение (8), пренебрегая в нем моментом сил трения Мmpсравнению с моментомM = mgr . (подобное пренебрежение будет правомочно, если величина груза такова, чтоmgr Мmp). Из уравнения (8) имеем
Следовательно,
(9)
Из полученного выражения понятно, как экспериментально проверить зависимость (7): нужно, выбрав постоянную массу груза т, измерять ускорение a при различных положениях R грузов m 0 на спицах. Результаты удобно изобразить в виде точек на координатной плоскости ХОУ , где
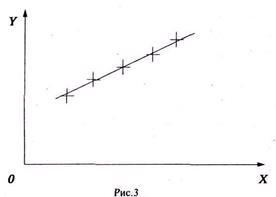
Если экспериментальные точки в пределах точности измерений ложиться на. прямую (рис.3), то это подтверждает зависимость (9), а значит и формулу
3. Измерения. Обработка результатов измерений.
1. Сбалансируйте маятник. Установите грузы 
на некотором расстоянии Rот оси маятника. При этом маятник должен находиться в состоянии безразличного равновесия. Проверьте, хорошо ли сбалансирован маятник. Для этого маятник следует несколько раз привести во вращение и дать возможность остановиться. Если маятник останавливается в различных отличающихся другот друга положениях, то он сбалансирован.
2. Оцените момент сил трения.Для этого, увеличивая массу груза т, найдите минимальное ее значениеm
1,
при котором маятник начинает вращаться. Повернув маятник на 180° по отношению к начальному положению, повторите описанную процедуру и найдите здесь минимальное значение т2. (Может оказаться, что 
по причине неточной балансировки маятника). Оцените по этим данным момент сил трения
3. Экспериментально проверьте зависимость (8). (В этой серии измерений момент инерции маятника должен оставаться постоянным =const). Укрепите на нити некоторый груз mmi, (i=1,2) и измерьте время t, за которое груз опускается на расстояние h. Измерение времени tдля каждого груза при постоянном значении hповторить 3 раза. Затем найдите среднее значение времени падения груза 
по формуле
и определите среднее значение углового ускорения
Подумайте, как оценить и оцените погрешность полученного значения 
. Описанные в этом пункте измерения повторите для 5 значений массы груза m. удовлетворяющих неравенству mmi, (i=1,2).
Результаты измерении занесите в таблицу
т |
r |
t1 |
t2 |
t3 |
|
|
h |
 |
 |
 |
М |  |
1 |
||||||||||||
2 |
||||||||||||
3 |
||||||||||||
4 |
||||||||||||
5 |
По полученным данным постройте график зависимости=
f
(
M
).
По графику определите момент инерции маятника и момент сил трения Мmp.
4. Проверьте экспериментально зависимость (7). Для этого, взяв постоянную массу грум m, определите ускорение а груза aпри 5 различных положениях на спицах грузов то .В каждом положении R измерения времени падения tгруза m. с высоты hповторите 3 раза. Найдите среднее значение времени падения:
и определите среднее значение ускорения груза
Результаты измерений занесите в таблицу
R |
t1 |
t2 |
t3 |
|
|
h |
|
|
|
1 |
|||||||||
2 |
|||||||||
3 |
|||||||||
4 |
|||||||||
5 |
По полученным данным рассчитайте величины 
и 
и постройте графикy
=
f
(
x
).
Для построения графика удобно сначала заполнить таблицу
Таблица
1 |
2 |
3 |
4 |
5 |
x |
||||
|
||||
y |
||||
|
5. Объясните полученные результаты. Сделайте выводы, находятся ли результаты экспериментов в соответствии с теорией.
4. Контрольные вопросы
1. Что мы называем абсолютно твердым телом? Какое уравнение описывает вращение твердого тела относительно неподвижной оси?
2. Получите выражение для момента импульса икинетической энергиитвердого тела, вращающегося вокруг неподвижной оси.
3. Что называют моментом инерции твердого тела относительно некоторой оси? Сформулируйте и докажите теорему Гюйгенса-Штейнера.
4. Какие измерения в проведенных Вами экспериментах вносилинаибольшую погрешность? Что необходимо сделать для уменьшения этойпогрешности?
Примеры решения задач по теме «Динамика вращательного движения твердого тела вокруг неподвижной оси»
Задача №1
Условие задачи:
Маховик в виде диска массой m=50 кг и радиусом r=20 см был раскручен до частоты вращения n1=480 мин-1 и затем предоставлен самому себе. Вследствие трения маховик остановился. Найти момент M сил трения, считая его постоянным для двух случаев: 1) маховик остановился через t=50 с; 2) маховик до полной остановки сделал N=200 оборотов.
 |
Задача №2
Условие задачи:
Платформа в виде диска радиусом R=1,5 м и массой m1=180 кг вращается по инерции около вертикальной оси с частотой n=10 мин-1. В центре платформы стоит человек массой m2=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?
Задача №3
Условие задачи:
Стержень длиной l=1,5 м и массой M=10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня (рис. 3.6). В середину стержня ударяет пуля массой m=10 г, летящая в горизонтальном направлении со скоростью v0=500 м/с, и застревает в стержне. На какой угол отклонится стержень после удара?
 |
Список используемой литературы
Основная
1.Учеб. для 10 кл. шк. и кл. с углубл. изуч. физики/О. Ф. Кабардин, В. А. Орлов, Э. Е. Эвенчик и др.; Под ред. А. А.Пинского. – 3-е изд.: М.: Просвещение, 1997.
2.Факультативный курс физики /О. Ф. Кабардин, В. А. Орлов, А. В. Пономарева. - М.: Просвещение, 1977.
3.Дополнительная
4.Ремизов А. Н. Курс физики: Учеб. для вузов / А. Н. Ремизов, А. Я. Потапенко. - М.: Дрофа, 2004.
5.Трофимова Т. И. Курс физики: Учеб. пособие для вузов. М.: Высшая школа, 1990.
Интернет
1.http://ru.wikipedia.org/wiki/
2.http://elementy.ru/trefil/21152
3.http://www.physics.ru/courses/op25part1/content/chapter1/section/paragraph23/theory.html и др.