Моделирование парожидкостного равновесия в четырехкомпонентной смеси ацетонтолуолн-бутанолдиметилформамид
СОДЕРЖАНИЕ: Оглавление Введение 1. Литературный обзор Термодинамико-топологический анализ структур диаграмм фазового равновесия Закономерности векторного поля нод и скалярного поля равновесных температур. Уравнение их взаимосвязиОглавление
Введение
1. Литературный обзор
Термодинамико-топологический анализ структур диаграмм фазового равновесия
Закономерности векторного поля нод и скалярного поля равновесных температур. Уравнение их взаимосвязи
Нелокальные закономерности диаграмм фазового равновесия жидкость–пар
Единичные ![]() -многообразия
-многообразия
Складки на скалярных полях равновесных температур кипения двухфазных многокомпонентных смесей
Экстрактивная ректификация как способ разделения многокомпонентных смесей
Математическое моделирование фазовых равновесий
Постановка задачи исследования
2. Расчетно-аналитическая часть
Число степеней свободы при изменении состава вдоль складок на скалярных полях равновесных температур двухфазных четырехкомпонентных смесей
Систематический анализ складок на поверхности равновесных температур четырехкомпонентных смесей
Выбор объекта и метода исследования
3. Проверка смеси ацетон–толуол–н-бутанол–диметилформамид по правилам азеотропии
4. Моделирование парожидкостного равновесия в четырехкомпонентной смеси ацетон–толуол–н-бутанол–диметилформамид
Система ацетон–толуол–н-бутанол
Система толуол–н-бутанол–диметилформамид
Система ацетон–н-бутанол–диметилформамид
Система ацетон–толуол–диметилформамид
Система ацетон–толуол–н-бутанол–диметилформамид
5. Обсуждение результатов
Выводы
Список литературы
Приложение
Приложение I
Приложение II
Приложение II-a
Приложение III
Приложение IV
Приложение V
Приложение VI
Введение
Для разделения азеотропных смесей в технологии основного органического и нефтехимического синтеза широкое распространение получили ректификационные методы. Создание научно обоснованных схем разделения сложных многокомпонентных смесей является неотъемлемой частью решения таких стратегически важных задач химической технологии, как экологическая безопасность, ресурсосбережение и повышение качества органических продуктов. В основе синтеза технологической схемы разделения многокомпонентных азеотропных смесей лежит термодинамико-топологический анализ структур диаграмм гетерогенного равновесия, помогающий выявить все возможные ограничения на выделение продуктов требуемого качества и определить предельные возможности процесса разделения.
Основной характеристикой диаграммы фазового равновесия разделяемой смеси является наличие особых точек, к которым относятся точки азеотропов и чистых компонентов. Наличие этих точек порождает сепаратрические многообразия, обусловленные векторным полем нод и складки на скалярных полях равновесных температур. Особенности поведения скалярных стационарных полей температуры имеют практическое значение. Они в определенной степени объясняют ход траектории процесса экстрактивной ректификации смесей в присутствии разделяющего агента, которая проходит через минимум или максимум температуры.
В данной работе на примере системы ацетон–толуол–н-бутанол–диметилформамид был изучен ход поверхности складки на скалярном поле равновесных температур и едничной ![]() –поверхности. Данная четырехкомпонентная система является смесью растворителей производства термостабилизатора стабилина-9.
–поверхности. Данная четырехкомпонентная система является смесью растворителей производства термостабилизатора стабилина-9.
В качестве метода исследования выбран вычислительный эксперимент с использованием проблемно-ориентированного комплекса CHEMCAD 5.2.0. Для моделирования парожидкостного равновесия системы при давлении 760 мм рт. ст. использовалось уравнение Вильсона. Получена полная математическая модель парожидкостного равновесия системы ацетон–толуол–н-бутанол–диметилформамид. В концентрационном тетраэдре построены изотермо–изобарические поверхности, поверхность складки на скалярном поле равновесных температур и едничная ![]() –поверхность.
–поверхность.
Работа выполнена на кафедре химии и технологии основного органического синтеза Московской государственной академии тонкой химической технологии имени М.В. Ломоносова.
1. Литературный обзор
1.1 Термодинамико-топологический анализ структур диаграмм фазового равновесия
Для технологий получения различных продуктов основного органического и нефтехимического синтеза характерны крупнотоннажность производства, широкий ассортимент получающихся веществ, которые используются в том числе в дальнейших синтезах, высокие требования к качеству получаемых продуктов. Поэтому при разработке технологии большая роль принадлежит блоку разделения реакционной смеси.
В производствах основного органического и нефтехимического синтеза применяются практически все известные методы разделения многокомпонентных смесей на чистые компоненты или фракции, имеющие товарную ценность. Это обусловлено постоянным расширением номенклатуры продуктов промышленного органического синтеза, широким диапазоном свойств синтезируемых веществ и повышением требований к их чистоте. Однако одним из основных процессов разделения многокомпонентных жидких смесей является ректификация, так как данный процесс отвечает специфике рассматриваемой отрасли промышленности.
Блок разделения является самым энергоемким. Энергозатраты на разделение зависят от технологической схемы разделения, а выбор той или иной схемы определяется физико-химическими и химическими свойствами как отдельных компонентов, так и разделяемых смесей в целом. На различных стадиях разделения смесей любой сложности выделяются фракции, содержащие разное число компонентов, которые, в свою очередь, также подвергаются разделению. В связи с этим возникает необходимость в исследовании физико-химических свойств всех смесей, составляющих первоначальную сложную смесь.
Синтез технологической схемы разделения многокомпонентной азеотропной системы – сложная многоуровневая задача. Первым этапом ее решения является метод термодинамико-топологического анализа (ТТА) структур диаграмм фазового равновесия. Этот метод впервые был предложен Серафимовым Л.А. [1] и рассмотрен в [3-6]. ТТА базируется на теоремах о локальных и нелокальных закономерностях структур диаграмм фазового равновесия, то есть включает в себя закономерности соотношения неподвижных стационарных точек векторных полей нод и особых точек скалярных полей различных свойств, обусловленных физико-химическими свойствами разделяемой смеси. При ТТА выявляются все возможные ограничения на те или иные варианты разделения данной смеси.
1.2 Закономерности векторного поля нод и скалярного поля равновесных температур. Уравнение их взаимосвязи
Фазовое равновесие жидкость–пар многокомпонентных смесей можно рассматривать в диаграммах, отражающих зависимости скалярных свойств от вектора состава, и в диаграммах, отражающих закономерности векторного поля нод жидкость–пар.
Рассмотрим закономерности векторного поля нод.
Представим фазовое равновесие некоторой многокомпонентной смеси в общем виде как функцию ![]() отображения множества (т.е. симплекса) составов одной фазы
отображения множества (т.е. симплекса) составов одной фазы ![]() в множество (т.е. симплекс) составов другой фазы
в множество (т.е. симплекс) составов другой фазы ![]() :
:
![]() , (1.1)
, (1.1)
где ![]() означает, что каждому составу первой фазы
означает, что каждому составу первой фазы ![]() , который характеризуется набором концентраций компонентов
, который характеризуется набором концентраций компонентов ![]() , ставится в соответствие термодинамически равновесный ему состав второй фазы
, ставится в соответствие термодинамически равновесный ему состав второй фазы ![]() , который характеризуется своим набором концентраций
, который характеризуется своим набором концентраций ![]() .
.
Данное соответствие обеспечивается для бинарной смеси построением кривой равновесия жидкость–пар. Для многокомпонентной смеси такое построение в принципе невозможно, так как состав каждой из фаз имеет уже не скалярную, а векторную природу.
Основой, позволяющей осуществить различные процессы разделения, является то, что в общем случае составы равновесных фаз различаются. Степень этого различия в бинарных смесях определяется степенью удаления кривой фазового равновесия от диагонали в диаграмме ![]() . Пример кривых фазового равновесия жидкость–пар для бинарных зеотропных и азеотропных смесей приведен на рис. 1.1.
. Пример кривых фазового равновесия жидкость–пар для бинарных зеотропных и азеотропных смесей приведен на рис. 1.1.

![]()
1
2
3
![]()
Рис. 1.1. Кривые фазового равновесия жидкость–пар бинарных зеотропных (1) и азеотропных смесей: с минимумом (2) и максимумом (3) температуры кипения.
Для многокомпонентных смесей, совместив концентрационный симплекс одной фазы на концентрационный симплекс другой, соединим равновесные фазы некоторыми отрезками, указанная степень отличия будет определяться длиной каждого отрезка. Отрезки такого типа называются равновесными нодами (например, нода жидкость–пар, нода жидкость–жидкость).
С учетом того, что энтропия жидкой фазы (1) меньше, чем энтропия паровой фазы (2), будем считать, что вектор ноды будет направлен от состава жидкости к составу пара, и наоборот. Таким образом, нода ![]() – это некоторый вектор, получаемый как разность состава фаз:
– это некоторый вектор, получаемый как разность состава фаз:
![]() , (1.2)
, (1.2)
Противоположно направленный вектор называется ренодой.
![]() (1.3)
(1.3)
Очевидно, что:
![]() (1.4)
(1.4)
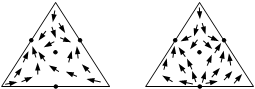
Совокупность нод образует в совмещенном концентрационном симплексе некоторое векторное поле, покрывающее весь симплекс или его часть. Данное векторное поле, которое является стационарным, то есть не зависит от времени, является геометрическим образом, отражающим физико-химическую природу рассматриваемой системы. На рис. 1.2 приведены векторные поля нод жидкость–пар для трехкомпонентных смесей.
Точки, в которых длина вектора ноды равна нулю, а направление его неопределенно, называются неподвижными точками функции отображения или особыми точками диаграммы фазового равновесия. К таким точкам относятся, например, в случае фазового равновесия жидкость–пар точки, соответствующие чистым компонентам, и точки, соответствующие бинарным, тройным, четверным и другим азеотропам. В этих точках составы равновесных фаз равны друг другу, а для случая азеотропов в соответствии с законом Гиббса–Коновалова наблюдается экстремум температуры (при закрепленном давлении) или давления (при закрепленной температуре) [2].

3.0.0-1 3.1.0-1а 3.1.0-1б 3.1.0-2
3.1.1-1а 3.1.1-1б 3.1.1-2 3.2.0-1
3.2.0-2а 3.2.0-2б 3.2.0-2в 3.2.1-1

3.2.1-2а 3.2.1-2б 3.2.1-3а 3.2.1-3б


3.3.0-1а 3.3.0-1б 3.3.0-2 3.3.1-1а

3.3.1-1б 3.3.1-1в 3.3.1-2 3.3.1-3а
3.3.1-3б 3.3.1-4
Рис. 1.2. Векторные поля нод жидкость–пар для диаграмм различных классов и видов.
Различают несколько типов особых точек, каждому из которых соответствует определенный ход дистилляционных линий. Например, для случая трехкомпонентных смесей в случае узловых точек все траектории сходятся в особой точке (устойчивый узел) или выходят из нее (неустойчивый узел). В случае седел – часть траекторий сходятся к особой точке, часть – выходят из нее и часть траекторий имеют в окрестности особой точки гиперболический ход, сначала приближаясь к ней, а потом удаляясь от нее. На рис. 1.3 показан ход дистилляционных линий в окрестностях особых точек различных типов.



(а) (б) (в)
Рис. 1.3. Особые точки траектории дистилляции в трехкомпонентных системах:
(а) – неустойчивый узел; (б) – устойчивый узел; (в) – седло.
Таковы закономерности векторного поля равновесных нод жидкость–пар. Далее рассмотрим закономерности скалярного поля равновесных температур.
Фазовое равновесие жидкость–пар многокомпонентных смесей можно рассматривать в диаграммах, отражающих зависимости скалярных свойств от вектора состава. Например, диаграмма равновесия может быть представлена полем равновесных температур кипения жидкой фазы системы при заданном давлении. На диаграммах состав–свойство для n -компонентной двухфазной системы любое свойство, выраженное некоторой скалярной величиной, не зависящей от времени, индуцирует над концентрационным симплексом непрерывное стационарное скалярное поле, структура которого усложняется с увеличением компонентности системы. Для трехкомпонентной системы диаграмма равновесия характеризуется некоторыми линиями, называемыми изотермоизобарами. Для четырехкомпонентных систем изотермоизобары являются уже некоторыми поверхностями и т.д. Скалярное стационарное поле равновесных температур может быть представлено и в векторном виде с помощью вектора-градиента. Этот вектор всегда направлен в сторону наибольшего возрастания поля (в данном случае поля температур) ортогонально к многообразию уровня. Вектор-градиент характеризуется набором частных производных величины свойства (температуры) по концентрациям компонентов:
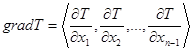 (1.5)
(1.5)
Производная этого градиента по времени равна нулю, что отражает стационарность рассматриваемого поля:
![]() (1.6)
(1.6)
Использование градиента позволяет представить скалярное поле в виде некоторых линий, в каждой точке которой направление касательной к этой линии задается градиентом, то есть мгновенная скорость продвижения по такой линии численно равна градиенту. Мгновенное изменение вектора состава, равное dX , будет также вектором, принадлежащим концентрационному симплексу и коллинеарному градиенту. Следовательно, имеем следующую функциональную зависимость:
![]() (1.7)
(1.7)
Или теоретически можно представить себе движение фигуративной точки в поле градиента температуры, при котором в каждой точке траектории градиент лежит на касательной прямой к этой траектории. Такое движение описывается системой уравнений вида [6]:
![]() (1.8)
(1.8)
Дифференциал температуры в общем виде представляется как скалярное произведение градиента температуры на вектор изменения состава одной из фаз. Для жидкой фазы:
![]() (1.9)
(1.9)
Согласно уравнению (1.9), равенство нулю дифференциала равновесной температуры ![]() будет реализовываться в двух случаях:
будет реализовываться в двух случаях:
1) Вектор-градиент равновесной температуры равен нулю ![]() , то есть равны нулю все частные производные скалярной величины по переменным концентрациям компонентов. Этот случай характеризует особую точку температурной поверхности размерности
, то есть равны нулю все частные производные скалярной величины по переменным концентрациям компонентов. Этот случай характеризует особую точку температурной поверхности размерности ![]() , которая может быть минимумом, максимумом, минимаксом.
, которая может быть минимумом, максимумом, минимаксом.
2) Векторы ![]() и
и ![]() ортогональны друг другу, и их произведение равно нулю. Это условие соответствует движению вдоль изотермоизобарического многообразия, вдоль которого
ортогональны друг другу, и их произведение равно нулю. Это условие соответствует движению вдоль изотермоизобарического многообразия, вдоль которого ![]() и
и ![]() .
.
Уравнение Ван-дер-Ваальса–Сторонкина [7] – это математическая модель, описывающая равновесное распределение всех компонентов между фазами и устанавливающая соответствие между параметрами фазового перехода. Также это уравнение фазового обмена, связывающее фазовые эффекты (объемный, энтропийный, эффект химических потенциалов), которые отражают локальное поведение системы при переходе бесконечно малого количества одной фазы в конечное количество другой фазы.
В общем виде для двухфазной ![]() -компонентной системы уравнение Ван-дер-Ваальса–Сторонкина записывается так [7]:
-компонентной системы уравнение Ван-дер-Ваальса–Сторонкина записывается так [7]:
![]() (1.10)
(1.10)
Уравнение связи между векторным полем нод и скалярным полем равновесных температур [3, 6, 8] позволяет легко анализировать фазовое равновесие для многокомпонентных смесей. Данное уравнение записывается как система уравнений в частных производных и при ![]() имеет следующий вид:
имеет следующий вид:
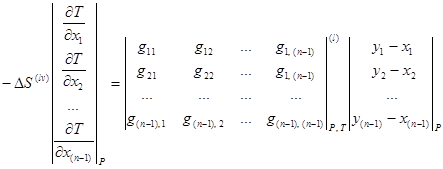 (1.11)
(1.11)
Для случая ![]() :
:
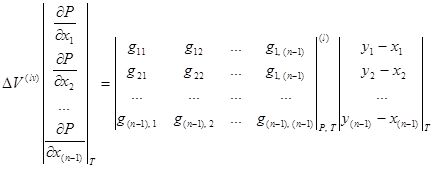 , (1.12)
, (1.12)
где ![]() – изменение энтропии при фазовом дифференциальном переходе бесконечно малого количества смеси из жидкости (
– изменение энтропии при фазовом дифференциальном переходе бесконечно малого количества смеси из жидкости (![]() ) в пар (
) в пар (![]() );
);
![]() – изменение объема при фазовом дифференциальном переходе бесконечно малого количества смеси из жидкости (
– изменение объема при фазовом дифференциальном переходе бесконечно малого количества смеси из жидкости (![]() ) в пар (
) в пар (![]() );
);
![]() – вторые производные изобарно-изотермического потенциала Гиббса для жидкой (
– вторые производные изобарно-изотермического потенциала Гиббса для жидкой (![]() ) фазы;
) фазы;
![]() – концентрации
– концентрации ![]() -компонента в жидкой и паровой фазе соответственно.
-компонента в жидкой и паровой фазе соответственно.
В общем виде уравнения (1.11) и (1.12) можно представить так [3, 6, 8]:
![]() , (1.13)
, (1.13)
![]() (1.14)
(1.14)
С помощью оператора ![]() в уравнениях (1.13) и (1.14) связывают вектор-ноду жидкость–пар и градиент температуры (при
в уравнениях (1.13) и (1.14) связывают вектор-ноду жидкость–пар и градиент температуры (при ![]() ) или градиент давления (при
) или градиент давления (при ![]() ). На рис. 1.4 приведена общая картина расположения векторов, взаимосвязанных уравнением фазового обмена [8].
). На рис. 1.4 приведена общая картина расположения векторов, взаимосвязанных уравнением фазового обмена [8].
Как видно, в первом случае векторы ноды и градиента температур направлены в разные стороны и образуют между собой тупой угол; во втором – векторы ноды и градиента давлений направлены в одну сторону и образуют между собой острый угол, что объясняет знак «–» в уравнении (1.11). После действия оператора G вектор ноды изменяет свое направление и модуль и становится вектором ![]() . Вектор градиента после умножения на скалярный множитель изменяет свой модуль и также становится равным по величине вектору
. Вектор градиента после умножения на скалярный множитель изменяет свой модуль и также становится равным по величине вектору ![]() .
.
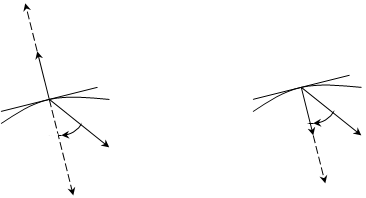
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(а) (б)
Рис. 1.4. Взаимное расположение изотермоизобарического многообразия, векторов ноды жидкость–пар и градиентов температуры (а) и давления (б) в трехкомпонентных системах.
Из сравнения уравнений (1.11) и (1.12) следует частный вывод. Для некоторого вектора состава жидкой фазы отнимем одно уравнение от другого. При определенных ![]() и
и ![]() получим следующий результат [8]:
получим следующий результат [8]:
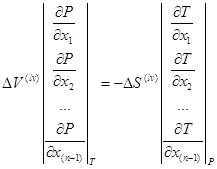 (1.15)
(1.15)
или:
![]() (1.16)
(1.16)
Поскольку ![]() и
и ![]() – некоторые скалярные множители, то для закрепленного состава системы градиенты стационарного поля температур кипения при
– некоторые скалярные множители, то для закрепленного состава системы градиенты стационарного поля температур кипения при ![]() и градиенты стационарного поля давлений при
и градиенты стационарного поля давлений при ![]() колинеарны. Последнее согласуется с физическим смыслом, так как в этом случае точка состава смеси принадлежит определенному изотермоизобарическому многообразию, которое является многообразием уровня как для температуры, так и для давления. Однако векторы имеют разный знак, и их линейная (в точке) комбинация всегда равна нулю:
колинеарны. Последнее согласуется с физическим смыслом, так как в этом случае точка состава смеси принадлежит определенному изотермоизобарическому многообразию, которое является многообразием уровня как для температуры, так и для давления. Однако векторы имеют разный знак, и их линейная (в точке) комбинация всегда равна нулю:
![]() (1.17)
(1.17)
Следовательно, эти два вектора всегда лежат на одной прямой, ортогональной многообразию уровня, и имеют противоположное направление.
Подробное исследование уравнений (1.11) и (1.12) было проведено в [8]. Отмечено, что полученные результаты можно использовать для выявления различных корреляций и тонких закономерностей фазового равновесия жидкость–пар в многокомпонентных системах, в частности:
- для определения взаимосвязи топографического представления равновесной температуры кипения смеси и хода ![]() -линий, в том числе единичных;
-линий, в том числе единичных;
- для определения экстремумов температуры (давления) по направлению;
- для корреляции хода изотермоизобар и коэффициентов распределения компонентов;
- для получения некоторых общих выводов относительно различных термодинамических свойств путём исследования полученных уравнений в избыточных функциях.
Подробное исследование свойств скалярных полей равновесных температур двухфазных трехкомпонентных систем было проведено в [9-11].
1.3 Нелокальные закономерности диаграмм фазового равновесия жидкость–пар
Индексом (![]() ) особой точки поля нод называют число поворотов вектора на 360° при обходе вокруг этой точки вдоль замкнутой линии, охватывающей эту точку. Если векторы поворачиваются на 360° при обходе особой точки, причем в ту же сторону, в какую совершается обход, то
) особой точки поля нод называют число поворотов вектора на 360° при обходе вокруг этой точки вдоль замкнутой линии, охватывающей эту точку. Если векторы поворачиваются на 360° при обходе особой точки, причем в ту же сторону, в какую совершается обход, то ![]() , а если нода поворачивается в противоположную сторону, то
, а если нода поворачивается в противоположную сторону, то ![]() . Если при обходе вектор-нода остается неподвижной или совершает равные колебания в стороны, то
. Если при обходе вектор-нода остается неподвижной или совершает равные колебания в стороны, то ![]() . Все простые (не особые) точки имеют индекс, равный нулю. Если обойти по замкнутой кривой некоторое многообразие, которое содержит несколько особых точек с разными индексами, то индекс многообразия (
. Все простые (не особые) точки имеют индекс, равный нулю. Если обойти по замкнутой кривой некоторое многообразие, которое содержит несколько особых точек с разными индексами, то индекс многообразия (![]() ), то есть число поворотов вектора-ноды на его границе, вдоль которой осуществляется движение, будет равен сумме индексов особых точек этого многообразия:
), то есть число поворотов вектора-ноды на его границе, вдоль которой осуществляется движение, будет равен сумме индексов особых точек этого многообразия:
![]() (1.18)
(1.18)
Для замкнутых многообразий, например сферы, индекс не зависит от конкретного векторного поля, размещенного на этой сфере, а характеризуется некоторым инвариантом – характеристикой Эйлера, которая в топологии определяется уравнением:
![]() , (1.19)
, (1.19)
где ![]() – размерность сферы.
– размерность сферы.
Алгебраическая сумма индексов особых точек равна на сфере характеристике Эйлера:
![]() (1.20)
(1.20)
Уравнение (1.20) было принято за основу в исследованиях общих законов построения фазовых диаграмм, характеризуемых разным числом особых точек различного типа. Как видно из этого уравнения, суммарный индекс сферы равен нулю, если m – нечетное число, и равен двум, если m – четное число. Таким образом, зная общий индекс сферы, можно задачу подсчета алгебраической суммы особых точек диаграммы фазового равновесия свести к задаче построения сферы из концентрационных симплексов той же размерности и подсчета повторяющихся при этом особых точек.
Если обозначить: ![]() – узлы с положительным индексом,
– узлы с положительным индексом, ![]() – узлы с отрицательным индексом,
– узлы с отрицательным индексом, ![]() – седла с положительным индексом,
– седла с положительным индексом, ![]() – седла с отрицательным индексом, то уравнение связи этих особых точек, предложенное Жаровым В.Т., имеет вид:
– седла с отрицательным индексом, то уравнение связи этих особых точек, предложенное Жаровым В.Т., имеет вид:
![]() , (1.21)
, (1.21)
где n
– число компонентов; k
– число ![]() составляющих п
-компонентной смеси, изменяющееся от 1 до п
; а
составляющих п
-компонентной смеси, изменяющееся от 1 до п
; а ![]() отражает повторяемость данной особой точки на сфере.
отражает повторяемость данной особой точки на сфере.
Используя несколько другой метод построения сферы из концентрационных симплексов, Серафимовым Л.А. было получено уравнение, в котором индекс «п
» относится к п
-компонентным азеотропам, а индекс «Г
» – к граничным особым точкам концентрационного симплекса, то есть к любому азеотропу, содержащему от ![]() до двух компонентов, и точкам, соответствующим чистым веществам:
до двух компонентов, и точкам, соответствующим чистым веществам:
![]() (1.22)
(1.22)
В отличии от уравнения (1.21), в уравнение (1.22) входят только те особые точки, которые при «склеивании» симплексов и отображении их на сферу имеют индекс +1 или –1. Ряд граничных точек, которые при склеивании имеют индекс 0 (сложные особые точки), в уравнение не входят. К таким точкам относятся положительно-отрицательные узлы ![]() , седло–узлы
, седло–узлы ![]() и
и ![]() , положительно-отрицательные седла
, положительно-отрицательные седла ![]() .
.
Уравнения (1.21) и (1.22) называют правилами азеотропии. Они являются составляющими единой системы диофантовых уравнений и взаимно дополняют друг друга. Для трехкомпонентных систем оба уравнения приводят к виду, полученному Гуриковым Ю.В. [12]:
![]() (1.23)
(1.23)
Здесь нижний индекс соответствует числу компонентов. Уравнения (1.21) и (1.22) применимы к любой азеотропной многокомпонентной смеси и описывают нелокальные закономерности фазовых диаграмм. Каждое из уравнений позволяет воспроизвести все диаграммы фазового равновесия, удовлетворяющие термодинамическим и топологическим закономерностям.
Все возможные не противоречащие термодинамике гетерогенных смесей диаграммы траекторий открытого равновесного испарения, которые однозначно характеризуют векторные поля нод трехкомпонентных смесей, а так же соответствующие векторным полям скалярные поля равновесных температур представлены в работах [2, 4, 6].
1.4 Единичные ![]() -многообразия
-многообразия
Относительная летучесть компонентов ![]() и
и ![]() есть отношение их коэффициентов распределения
есть отношение их коэффициентов распределения ![]() и
и ![]() между паровой и жидкой фазой, находящихся в равновесии, соответственно:
между паровой и жидкой фазой, находящихся в равновесии, соответственно:
![]() (1.24)
(1.24)
При этом ![]() , а
, а ![]() . Таким образом, можем записать:
. Таким образом, можем записать:
![]() (1.25)
(1.25)
Относительная летучесть может так же быть выражена с использованием коэффициента активности ![]() , учитывающего отклонение от идеальности компонента
, учитывающего отклонение от идеальности компонента ![]() в жидкой фазе (в предположении, что паровая фаза смесь идеальных газов) и давления насыщенных паров чистого компонента
в жидкой фазе (в предположении, что паровая фаза смесь идеальных газов) и давления насыщенных паров чистого компонента ![]() в системе
в системе ![]() [13]:
[13]:
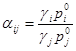 (1.26)
(1.26)
Единичное ![]() -многообразие характеризуется тем, что вдоль него одна относительная летучесть или несколько относительных летучестей равны единице. В [14] были впервые рассмотрены единичные
-многообразие характеризуется тем, что вдоль него одна относительная летучесть или несколько относительных летучестей равны единице. В [14] были впервые рассмотрены единичные ![]() -многообразия для различных типов диаграмм фазового равновесия двухфазных трехкомпонентных систем, там же приведено следующее определение: единичным
-многообразия для различных типов диаграмм фазового равновесия двухфазных трехкомпонентных систем, там же приведено следующее определение: единичным ![]() -многообразием, вложенным в концентрационное пространство, соответствующее жидкой или паровой фазе, принято называть такое многообразие, для которого относительная летучесть определенной пары компонентов или некоторой совокупности пар компонентов равна единице.
-многообразием, вложенным в концентрационное пространство, соответствующее жидкой или паровой фазе, принято называть такое многообразие, для которого относительная летучесть определенной пары компонентов или некоторой совокупности пар компонентов равна единице.
Кратностью ![]() единичного
единичного ![]() -многообразия называется число пар компонентов, для которого выполняется следующее равенство [15, 16]:
-многообразия называется число пар компонентов, для которого выполняется следующее равенство [15, 16]:
![]() (1.27)
(1.27)
Если в концентрационном симплексе отсутствуют единичные ![]() -многообразия, то кратность равна нулю. В этом случае концентрационный симплекс можно рассматривать как единичное
-многообразия, то кратность равна нулю. В этом случае концентрационный симплекс можно рассматривать как единичное ![]() -многообразие нулевой кратности. Единичное
-многообразие нулевой кратности. Единичное ![]() -многообразие кратности
-многообразие кратности ![]() соответствует п
-компонентному азеотропу, то есть азеотропной точке, расположенной во внутренней области концентрационного симплекса. Таким образом размерность
соответствует п
-компонентному азеотропу, то есть азеотропной точке, расположенной во внутренней области концентрационного симплекса. Таким образом размерность ![]() единичных
единичных ![]() -многообразий изменяется в интервале:
-многообразий изменяется в интервале:
![]() (1.28)
(1.28)
Единичное ![]() -многообразие кратности 1 имеет размерность
-многообразие кратности 1 имеет размерность ![]() , то есть на единицу меньше размерности концентрационного симплекса; последняя в свою очередь равна
, то есть на единицу меньше размерности концентрационного симплекса; последняя в свою очередь равна ![]() . Таким образом это многообразие делит концентрационный симплекс на две области: область
. Таким образом это многообразие делит концентрационный симплекс на две области: область ![]() и область
и область ![]() .
.
При ![]() размерность единичного
размерность единичного ![]() -многообразия равна
-многообразия равна ![]() и т.д. В общем случае можно записать [15, 16]:
и т.д. В общем случае можно записать [15, 16]:
![]() (1.29)
(1.29)
Поэтому единичное ![]() -многообразие любой кратности выше единицы можно рассматривать как некоторое многообразие, образованное пересечением
-многообразие любой кратности выше единицы можно рассматривать как некоторое многообразие, образованное пересечением ![]() единичных
единичных ![]() -многообразий, при этом
-многообразий, при этом ![]() .
.
Для трехкомпонентных систем в [14] показано, что тройной азеотроп соответствует точке пересечения двух линий, вдоль которых ![]() и
и ![]() . Через эту точку пройдет также и третья линия
. Через эту точку пройдет также и третья линия ![]() , но она уже принадлежит зависимой паре компонентов. Вдоль линии
, но она уже принадлежит зависимой паре компонентов. Вдоль линии ![]() будут наблюдаться условные экстремумы температур относительно линий, вдоль которых химический потенциал второго компонента равен постоянной величине. Линии
будут наблюдаться условные экстремумы температур относительно линий, вдоль которых химический потенциал второго компонента равен постоянной величине. Линии ![]() и
и ![]() являются линиями условных экстремумов температур, относительно изопотенциала первого и третьего компонентов соответственно. Если паровая фаза идеальна, то изопотенциалы и линии
являются линиями условных экстремумов температур, относительно изопотенциала первого и третьего компонентов соответственно. Если паровая фаза идеальна, то изопотенциалы и линии ![]() соответствующих компонентов совпадают. Каждый бинарный азеотроп
соответствующих компонентов совпадают. Каждый бинарный азеотроп ![]() трехкомпонентной системы
трехкомпонентной системы ![]() дает начало одной линии
дает начало одной линии![]() , которая заканчивается на одной из сторон треугольника Гиббса –
, которая заканчивается на одной из сторон треугольника Гиббса – ![]() или
или ![]() . Рассмотренные линии
. Рассмотренные линии ![]() являются также линиями условных экстремумов химических потенциалов относительно изотермоизобар. Поэтому в точке окончания
являются также линиями условных экстремумов химических потенциалов относительно изотермоизобар. Поэтому в точке окончания ![]() -линий химический потенциал компонента имеет наивысшее значение вдоль той изотермоизобары, которая приходит в эту же точку. Эти выводы [14] были получены авторами из анализа уравнения Ван-дер-Ваальса–Сторонкина.
-линий химический потенциал компонента имеет наивысшее значение вдоль той изотермоизобары, которая приходит в эту же точку. Эти выводы [14] были получены авторами из анализа уравнения Ван-дер-Ваальса–Сторонкина.
В [17] было рассмотрено взаимное расположение некоторых изомногообразий в диаграммах равновесия двухфазных многокомпонентных смесей.
1.5 Складки на скалярных полях равновесных температур двухфазных многокомпонентных смесей
Основным вопросом организации процесса разделения является определение предельно возможных составов получаемых продуктов или отдельных фракций с необходимым выходом. Для любой зеотропной многокомпонентной системы решение этого вопроса связано только с эффективностью процесса и протяженностью аппарата, в котором осуществляется разделение. Для азеотропных многокомпонентных систем появляются иные ограничения, связанные с особенностью фазовых диаграмм. В большинстве диаграмм концентрационный симплекс распадается на ряд областей дистилляции. Как было показано в [1] при бесконечном флегмовом числе границами между этими областями являются сепаратрические многообразия. Крутизна траекторий ректификации при конечных флегмовых числах больше таковой при бесконечном флегмовом числе, и потому траектории ректификации не должны выходить за пределы, определяемые сепаратрическим многообразием [18].
В работах [19-22] было показано, что границами между областями ректификации в трехкомпонентных системах являются, в частности, сепаратрисы, а сами границы бывают двух типов: сепаратрисы и граничные траектории. В [23] было отмечено, что границы между областями определяются совокупностью предельно возможных составов конечных продуктов, получаемых для множества исходных составов. При этом было подчеркнуто, что определенную роль играют складки на поверхности равновесной температуры. А также учитывали тот факт, что в ректификационной колонне температура непрерывно растет от дистиллята к кубовому продукту. В [24] определяли границу между областями ректификации в трехкомпонентных системах градиентным методом, совмещенным с поиском максимальной кривизны изотермоизобар. Границей между областями ректификации была линия наибыстрейшего спуска вдоль складки на поверхности равновесной температуры. В [25] установлено, что складки на поверхности равновесных температур, определяемые таким способом, не связаны с сепаратрическими многообразиями и не разделяют концентрационный симплекс на области развития процесса ректификации. В работах [24] и [25] определяли складку для скалярных полей равновесных температур (давлений) как «абсолютную складку».
Однако, в настоящей дипломной работе, как и в [7, 9-11, 26], каждую складку определяем по координатам, то есть относительно независимых концентраций. Складка, при этом, образуется всякий раз, когда одна из составляющих![]() , а именно
, а именно ![]() , где
, где ![]() для случая трехкомпонентной смеси. Так как градиент есть вектор, обладающий вполне определенными свойствами, то равенство нулю одной или нескольких составляющих
для случая трехкомпонентной смеси. Так как градиент есть вектор, обладающий вполне определенными свойствами, то равенство нулю одной или нескольких составляющих ![]() связано со специфическим направлением этого вектора в концентрационном симплексе. Положение вектора
связано со специфическим направлением этого вектора в концентрационном симплексе. Положение вектора ![]() легко анализировать в треугольнике Розебума, как представлено в [11]. Если движение некоторой точки происходит вдоль изотермоизобары: условие
легко анализировать в треугольнике Розебума, как представлено в [11]. Если движение некоторой точки происходит вдоль изотермоизобары: условие 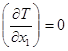 равносильно условию
равносильно условию ![]() в одной точке (т. О), в то время как на всем изотермоизобарическом многообразии
в одной точке (т. О), в то время как на всем изотермоизобарическом многообразии ![]() , а
, а 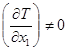 ; точка (т. О), в которой
; точка (т. О), в которой ![]() , идентична точке касания линии
, идентична точке касания линии ![]() и изотермоизобары. В этом случае вектор
и изотермоизобары. В этом случае вектор ![]() , который всегда был ортогонален вектору
, который всегда был ортогонален вектору ![]() , имеет составляющую
, имеет составляющую ![]() , в то время как
, в то время как ![]() (то есть
(то есть ![]() ). Проекция вектора-градиента температуры на ось
). Проекция вектора-градиента температуры на ось ![]() равна нулю. Следовательно,
равна нулю. Следовательно, 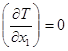 . Проекция же вектора
. Проекция же вектора ![]() на ось
на ось ![]() так же равна нулю (
так же равна нулю (![]() ), то есть дифференциал температуры – скалярное произведение векторов
), то есть дифференциал температуры – скалярное произведение векторов ![]() и
и ![]() . Соединив все т. О, в которых
. Соединив все т. О, в которых 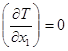 на каждой изотермоизобаре, получим кривую, которая и будет складкой на поле равновесных температур (для случая трехкомпонентных смесей).
на каждой изотермоизобаре, получим кривую, которая и будет складкой на поле равновесных температур (для случая трехкомпонентных смесей).
Известно [7], что наличие складок при ![]() на скалярном поле равновесных температур кипения (конденсации) двухфазных многокомпонентных систем так же как и при
на скалярном поле равновесных температур кипения (конденсации) двухфазных многокомпонентных систем так же как и при ![]() на скалярном поле равновесных давлений порождается азеотропией. При этом складка, как правило, начинается в точке азеотропа и может оканчиваться: в точке другого азеотропа; в точке чистого компонента; вырождаясь при приближении к какому-то элементу симплекса.
на скалярном поле равновесных давлений порождается азеотропией. При этом складка, как правило, начинается в точке азеотропа и может оканчиваться: в точке другого азеотропа; в точке чистого компонента; вырождаясь при приближении к какому-то элементу симплекса.
В [11] исследование складок проводили с помощью уравнения связи векторного поля нод и скалярного поля равновесных температур [3, 6, 8]. На основе анализа поведения систем классов 3.1.0-1а и 3.1.0-2 в сечениях концентрационного треугольника показано, что линия складки температур кипения и единичная ![]() -линия не совпадают, что может служить объяснением наличия на траекториях процесса экстремума температуры, не связанного с азеотропией.
-линия не совпадают, что может служить объяснением наличия на траекториях процесса экстремума температуры, не связанного с азеотропией.
Основные свойства скалярных полей равновесных температур и единичных ![]() -линий при атмосферном давлении изучены на примере двухфазных трехкомпонентных систем ацетон–гексан–этанол класса 3.2.0-26, которая также была исследована в [25], ацетон–метанол–вода класса 3.1.0-1а, метилацетат–хлороформ–бензол класса 3.1.0-2, бензол–циклогексан–1-пропанол класса 3.3.1-2. В качестве метода исследования выбран вычислительный эксперимент с использованием проблемно-ориентированного комплекса CHEMCAD 5.2.0. Получены полные математические модели парожидкостного равновесия в трехкомпонентных системах. Моделирование проводилось с использованием уравнения Вильсона. В концентрационных треугольниках построены поля изотермоизобар, линии складок температурной поверхности и единичные
-линий при атмосферном давлении изучены на примере двухфазных трехкомпонентных систем ацетон–гексан–этанол класса 3.2.0-26, которая также была исследована в [25], ацетон–метанол–вода класса 3.1.0-1а, метилацетат–хлороформ–бензол класса 3.1.0-2, бензол–циклогексан–1-пропанол класса 3.3.1-2. В качестве метода исследования выбран вычислительный эксперимент с использованием проблемно-ориентированного комплекса CHEMCAD 5.2.0. Получены полные математические модели парожидкостного равновесия в трехкомпонентных системах. Моделирование проводилось с использованием уравнения Вильсона. В концентрационных треугольниках построены поля изотермоизобар, линии складок температурной поверхности и единичные ![]() -линии. Авторами [9, 11] было установлено, что:
-линии. Авторами [9, 11] было установлено, что:
1) линии складок и единичных ![]() -линий пересекаются только в точках азеотропов;
-линий пересекаются только в точках азеотропов;
2) возможен случай, когда складка примыкает к ребру концентрационного треугольника, причем начинается и заканчивается на этом же ребре (система ацетон-метанол-вода);
3) количество складок в системе не зависит от количества азеотропных точек (что подтверждено примерами всех изученных трехкомпонентных систем).
Выявленные закономерности диаграмм скалярных стационарных полей температур и векторных полей нод двухфазных трехкомпонентных систем имеют практическое значение. Они в определенной степени объясняют ход траектории процесса экстрактивной ректификации бинарных смесей в присутствии разделяющего агента, которая проходит через минимум или максимум температуры.
Если построить зависимость паровой и жидкой фаз от их состава, то в силу смещения этих кривых относительно друг друга нода жидкость–пар, выраженная в относительных концентрациях, имеет конечную длину. В связи с этим относительный экстремум по температуре, обусловленный складкой на поверхности равновесных температур, не является особой точкой диаграммы и может быть пройден траекторией экстрактивной ректификации.
1.6 Экстрактивная ректификация как способ разделения многокомпонентных смесей
Создание научно обоснованных схем разделения сложных многокомпонентных систем является неотъемлемой частью решения таких важных задач химической технологии, как экологическая безопасность, ресурсосбережение, повышение качества органических продуктов. Эффективность принимаемых решений в значительной степени определяется особенностями технологии основного органического синтеза. В силу многотоннажности и непрерывности процессов даже незначительное улучшение их количественных показателей (повышение степени извлечения ценных веществ и содержания целевых компонентов в продуктовых потоках, снижение кратности рециклов и др.) дает ощутимую экономию материальных и энергетических ресурсов.
В основе большинства методов ректификационного разделения азеотропных систем лежит фундаментальный принцип перераспределения полей концентраций (ПППК) между областями ректификации. Его реализация базируется на специфике фазового поведения жидких систем и определяет структуру разделительного комплекса как совокупности аппаратов, охваченных обратными связями (рециклами).
Весьма перспективным для разделения азеотропных систем и зеотропных систем с относительной летучестью компонентов, близкой к единице, является процесс экстрактивной ректификации (ЭР). Необходимыми условиями его реализации являются выбор селективного разделяющего агента (РА) и организация разноуровневой подачи исходной системы и РА в колонну. В данном случае ПППК в присутствии разделяющих агентов, проявляется следующим образом: за счет направленного изменения относительной летучести разделяемых компонентов и динамической системы процесса исходная смесь, характеризующаяся наличием нескольких областей ректификации, делится как зеотропная, характеризующаяся наличием одной области ректификации.
Основные требования к селективным растворителям рассмотрены в [27], пути поиска и выбора растворителей – в [28].
Комплексы ЭР в большинстве случаев используются для разделения бинарных азеотропных систем. В то же время в технологии основного органического синтеза и смежных отраслях актуальной является проблема выделения целевых продуктов и регенерации растворителей из сложных многокомпонентных смесей. Исследованию некоторых аспектов этой проблемы посвящена работа [29]. Для разделения четырехкомпонентных смесей растворителей производства термостабилизатора стабилина–9 в [29] предложены энергоемкие схемы разделения с использованием комплексов, ориентированных на реализацию ПППК в присутствии селективных РА. К числу таких систем принадлежит и система ацетон–толуол–н-бутанол–диметилформамид [28], выбранная в настоящем дипломном проекте в качестве объекта исследования.
В [30] изучались режимы ректификации реальных зеотропных и азеотропных бинарных систем в колоннах с различной организацией внешних потоков. В качестве метода исследования был выбран расчетный эксперимент с использованием проблемно-ориентированного комплекса ChemCad. Моделирование парожидкостного равновесия и расчет ректификации осуществляли с применением уравнения NRTL. Авторы [30] исследовали влияние различных статических параметров на профиль температур и концентраций по высоте аппарата. Для каждой из исходных систем была проведена серия вычислительных экспериментов. Анализ расчетных данных показал, что при ректификации всех изученных смесей распределение температур (компонентов) по высоте колонны при организации противотока двух питаний характеризуется наличием экстремумов, что свидетельствует о наличии элементов обратной ректификации.
Исследование режимов ректификации в колоннах с различной организацией внешних потоков на основе одновременного анализа балансовых соотношений массы и тепла в сложных колоннах проводилось в работе [31]. В качестве исходных смесей были выбраны модельные бинарные зеотропные смеси с постоянной относительной летучестью компонентов. Данный выбор объясняется тем, что для освоения теории ректификации сложных азеотропных смесей, необходимо четко представлять основные закономерности ректификации бинарных смесей, из которых простейшими являются зеотропные смеси. Использовалась модель ректификации, базирующаяся только на статических характеристиках процесса. Для анализа ректификации бинарной смеси использовалась наряду с диаграммой парожидкостного равновесия и тепловая диаграмма.
Исследования проведенного типа [31] являются частью системных исследований экстрактивной и реэкстрактивной ректификации многокомпонентных смесей. В указанных процессах помимо эффекта, связанного с физико-химической составляющей, присутствуют эффекты, отличающие их от обычной ректификации и связанные с организацией внешних потоков. Последнее приводит к явлениям относительно обратной ректификации в определенной части колонны. Под относительно обратной ректификацией в реальных процессах подразумевается эффект, связанный со смешением вдоль аппарата (в верхней или нижней частях) РА с исходным раствором, при котором целевая пара компонентов продолжает делиться. Этот эффект должен существенно уменьшаться при интенсивном флегмировании и особо ярко проявляться при флегмовом числе, равном нулю, о чем свидетельствуют как результаты, полученные авторами [31].
Все экстрактивные гетерогенные системы подразделяют на системы с распределенными между фазами компонентами и системы с нераспределенными между фазами разделяющими агентами. Первые можно условно разделить на системы, в которых разделяющий агент является самым тяжелолетучим компонентом, и системы, в которых разделяющий агент является самым легколетучим компонентом. Для каждого из этих вариантов имеется свой типовой комплекс ректификационных колонн с определенной организацией потоков. Среди систем с тяжелолетучими разделяющими агентами можно выделить системы, в которых экстрактивный агент практически не летуч, то есть отсутствует в паровой фазе. Частным случаем экстрактивной ректификации с нелетучим агентом является солевая ректификация. Здесь в отличие от жидких нелетучих разделяющих агентов используют раствор соли или нескольких солей в разделяемой смеси. Применение смесей разделяющих агентов позволяет во многих случаях усилить экстрактивный эффект по сравнению с одиночным агентом. Приведенный перечень процессов разделения смесей в присутствии разделяющего агента по существу дает общую классификацию экстрактивных гетерогенных систем.
В работе [32] были получены общие уравнения, описывающие гетерогенные экстрактивные системы с несколькими нелетучими разделяющими агентами, в которых часть компонентов сосредоточена в жидкой фазе. А так же показано, что в сечениях, соответствующих постоянной концентрации нелетучего агента, эти системы не подчиняются закону Коновалова. Анализ этих уравнений и подробное рассмотрение трехкомпонентных систем с одним нелетучим агентом приведены в [33]. В работе [34] исследование было направлено на изучение особенностей фазового равновесия в четырехкомпонентной системе экстрактивной ректификации с одним нелетучим агентом. Было показано, что в различных сечениях концентрационного тетраэдра и на границах сечений закон Гиббса–Коновалова, согласно которому особые точки векторного поля нод жидкость–пар и скалярного поля равновесных температур должны совпадать, не действует.
1.7 Математическое моделирование фазовых равновесий
В настоящее время математическое моделирование является перспективным способом для анализа особенностей фазового равновесия и возможностей разделения многокомпонентных систем. Очевидным является многообразие принципов и методов оценки различных аспектов фазового равновесия. Лишь в очень редких случаях какой-либо один метод во всех отношениях превосходит другие. Это во многом затрудняет решение конкретных вопросов. Тем не менее, можно привести ряд рекомендаций, руководствуясь которыми можно получить достаточно точные результаты. Кроме того, на практике следует исходить из имеющегося опыта и аналогий.
Из множества уравнений состояния для корреляции коэффициентов активности с составом системы и до некоторой степени с температурой некоторые из них имеют более или менее разработанное теоретическое обоснование, другие являются чисто эмпирическими.
Математическое моделирование фазового равновесия жидкость–пар многокомпонентных смесей было описано в [35-37], моделирование равновесий жидкость–жидкость–пар – в работе [38]. В [39] авторы привели структуру концентрационного пространства и математическое описание фазового равновесия полиазеотропных смесей, а принципы его моделирования рассмотрены в [40]. Математическому моделированию фазового равновесия азеотропных смесей с учетом ассоциации в паровой фазе посвящена работа [41].
На сегодня наиболее широко применяются шесть различных видов корреляций коэффициентов активности. Рассмотрим каждый из них в отдельности.
Наиболее старым из числа применяемых на данный момент является уравнение Маргулеса.
Оно было получено в 1895г. Зачастую оно дает лучшие результаты по сравнению с другими уравнениями. Маргулесом было предложено представлять ![]() и
и ![]() в виде степенных рядов по составу:
в виде степенных рядов по составу:
![]() (1.30)
(1.30)
![]() (1.31)
(1.31)
для двухкомпонентных систем. Как правило, применяют линейные перегруппировки этих рядов, предложенные Карлсоном и Кольборном:
![]() (1.32)
(1.32)
![]() (1.33)
(1.33)
в которых существует простая зависимость между параметрами и коэффициентами активности при бесконечном разбавлении:
![]() (1.34)
(1.34)
![]() (1.35)
(1.35)
Избыточная энергия Гиббса, соответствующая этим уравнениям, составляет:
![]() (1.36)
(1.36)
Параметры уравнений (1.30) и (1.31) выводят следующим образом:
![]() (1.37)
(1.37)
![]() (1.38)
(1.38)
Эти параметры можно определить исходя из одной группы коэффициентов активности.
Редлихом и Кистером в 1948г. было предложено разложение в ряд, сходное по форме с уравнением (1.36):
![]() (1.39)
(1.39)
Уравнение (1.37) позволяет получить трехпараметрическое уравнение для коэффициентов активности:
![]() (1.40)
(1.40)
![]() (1.41)
(1.41)
Уравнение ван Лаара было выведено исходя из уравнения состояния Ван-дер-Ваальса, однако в силу того, что степень соответствия параметров последнего экспериментальным данным о коэффициентах активности низка, в настоящее время уравнение ван Лаара считается чисто эмпирическим.
Зависимость избыточной энергии Гиббса от мольных долей определяется выражением:
![]() , (1.42)
, (1.42)
из которого получаем следующие уравнения для коэффициентов активности:
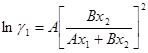 (1.43)
(1.43)
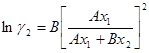 (1.44)
(1.44)
Параметры уравнения можно рассчитать исходя из одной группы данных о коэффициентах активности по уравнениям (1.45) и (1.46):
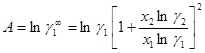 (1.45)
(1.45)
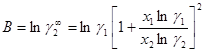 (1.46)
(1.46)
Блэком была предложена одна из линейных форм уравнения ван Лаара:
![]() (1.47)
(1.47)
Позднее было предложено несколько трехпараметрических модификаций уравнения ван Лаара с несколько улучшенной точностью представления. Так, Блэк прибавил еще один член к первоначальному определению избыточной энергии Гиббса, что дало:
![]() (1.48)
(1.48)
Уравнения Маргулеса, ван Лаара и связанные с ними алгебраические выражения характеризуются относительной простотой математического аппарата, легкостью оценки параметров по данным о коэффициентах активности и во многих случаях возможностью адекватного представления двухкомпонентных систем, довольно значительно отклоняющихся от идеальных, включая частично растворимые жидкие системы. Эти уравнения неприменимы к многокомпонентным системам, если отсутствуют параметры взаимодействия между тремя и более компонентами.
Уравнение Вильсона было предложено в 1964 году. При его разработке Вильсон исходил из того, что межмолекулярные взаимодействия зависят от «локальных концентраций», которые он выражал в объемных долях. Эти концентрации входят в вероятностные члены энергетического распределения Больцмана.
Теория локальных составов рассматривает раствор как упорядоченную структуру, в которой можно выделить для бинарной системы два вида молекулярных микроансамблей с определенным координационным числом. Один тип микроансамблей имеет в центре молекулу первого компонента, другой – молекулу второго компонента.
Согласно уравнению Вильсона избыточную энергию Гиббса можно представить следующим образом:
![]() , (1.49)
, (1.49)
где ![]() – приведенные значения параметров.
– приведенные значения параметров.
Применяя уравнение (1.50):
 , (1.50)
, (1.50)
можно найти коэффициенты активности:
![]() (1.51)
(1.51)
![]() (1.52)
(1.52)
![]() (1.53)
(1.53)
Было предпринято несколько попыток придать выводу уравнения Вильсона более строгое теоретическое обоснование и в некотором отношении улучшить его. Так, Моулрап вывел это и ряд других уравнений, используя одну из модификаций уравнения Ван-дер-Ваальса, в которой учитывается локальный состав, при этом он исходил в каждом случае из различных допущений. Нитта и Катаяма рассматривают уравнение Вильсона как вывод теории ассоциированных растворов. Цубока и Катаяма считают его частым случаем своих выкладок, предполагающим равенство молярных объемов компонентов.
Уравнение Вильсона позволяет точно представить равновесие жидкость–пар в двух- и многокомпонентных системах с использованием только параметров бинарного взаимодействия. К тому же оно отличается простотой. Еще одна положительная особенность этого уравнения состоит в том, что в нем заранее учтен температурный эффект [42].
Для представления равновесия жидкость–жидкость нельзя непосредственно применить уравнение Вильсона [4]; использование в этих целях его модификации, уравнения Цубоки–Катаямы , дает удовлетворительные результаты, хотя последнее не было подвергнуто такой тщательной экспериментальной проверке, как другие уравнения. Уравнение Вильсона положено в основу метода групповых вкладов ASOG, используемого для получения коэффициентов активности.
В [43] авторы определяли число корней уравнения Вильсона по данным о единственной бинарной точке. Термодинамический анализ этой модели с использованием парциальных избыточных функций был проведен в [44].
Уравнение NRTL (nonrandom two-liquid) для избыточной энергии Гиббса выводят, основываясь на теории, согласно которой жидкость в двухкомпонентной системы имеет ячеистую структуру, причем эти ячейки (кластеры) состоят из молекул типа 1 и 2, каждая из которых окружена такими же молекулами, которые в свою очередь имеют аналогичное окружение, и т.д.
Итоговое уравнение для избыточной энергии Гиббса имеет вид:
 (1.54)
(1.54)
![]() (1.55)
(1.55)
![]() (1.56)
(1.56)
![]() (1.57)
(1.57)
![]() , (1.58)
, (1.58)
где ![]() – Гиббсовы энергии взаимодействий между молекулами, причем подстрочным индексом j
указывают центральную молекулу;
– Гиббсовы энергии взаимодействий между молекулами, причем подстрочным индексом j
указывают центральную молекулу;
![]() – константа, принимаемая за характеристику заданности системы.
– константа, принимаемая за характеристику заданности системы.
Коэффициенты активности получают дифференцированием:
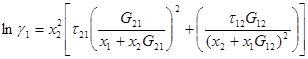 (1.59)
(1.59)
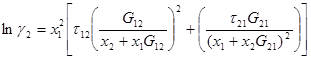 (1.60)
(1.60)
Эти уравнения содержат три независимых параметра ![]() ,
, ![]() и
и ![]() .
.
При помощи трехпараметрического уравнения NRTL можно, как правило, достаточно хорошо представить данные о равновесии в бинарных системах. Преимущество уравнения NRTL по сравнению с уравнениями Маргулеса и ван Лаара состоит в том, что его можно применять к многокомпонентным системам, основываясь только на бинарных параметрах, а по сравнению с уравнением Вильсона – в том, что его можно использовать для представления равновесия жидкость–жидкость. Кроме того, применительно к водным системам уравнение NRTL часто превосходит другие уравнения. Однако его недостаток состоит в том, что для каждой пары составляющих необходимы три параметра.
Термодинамический анализ модели NRTL с использованием концентрационных зависимостей избыточных функций был проведен в [45].
На концепции локальных составов основано так же предложенное Абрамсоном Д.С. и Праузницем Д.И. уравнение UNIQUAC (Universal Quasi Chemical). Используемая авторами модель предполагает, что избыточная энергия Гиббса обусловлена, во-первых, различием размеров и форм молекул (конфигурационная или комбинаторная составляющие) и, во-вторых, энергией взаимодействия молекул.
Коэффициенты активности имеют в этом случае вид:
![]() (1.61)
(1.61)
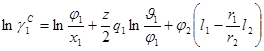 (1.62)
(1.62)
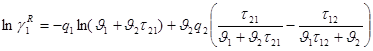 (1.63)
(1.63)
![]() (1.64)
(1.64)
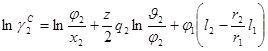 (1.65)
(1.65)
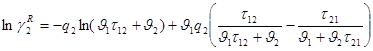 (1.66)
(1.66)
![]() (1.67)
(1.67)
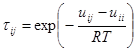 , (1.68)
, (1.68)
где ![]() – параметр площади компонента i
;
– параметр площади компонента i
;
![]() – параметр объема компонента i
;
– параметр объема компонента i
;
![]() – параметр взаимодействия между компонентами i
и j
;
– параметр взаимодействия между компонентами i
и j
; ![]() ;
;
![]() – координационное число,
– координационное число, ![]() ;
;
![]() – комбинаторная часть коэффициента активности компонента i
;
– комбинаторная часть коэффициента активности компонента i
;
![]() – остаточная часть коэффициента активности компонента i
;
– остаточная часть коэффициента активности компонента i
;
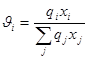 – доля площади компонента i
;
– доля площади компонента i
;
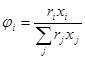 – объемная доля компонента i
.
– объемная доля компонента i
.
Маурер и Праузниц предложили более простой способ вывода этого уравнения, они же разработали трехпараметрическую модификацию уравнения, которую, однако, невозможно распространить на многокомпонентные системы.
Уравнение UNIQUAC – наиболее сложное в алгебраическом отношении, хотя в нем используется только по два параметра для каждой пары компонентов. В уравнении учитываются сведения о площадях поверхности и объемах молекул чистых компонентов, которые можно определить по данным о структуре, в силу чего этот метод представляется особенно эффективным применительно к смесям, молекулы которых значительно различаются по размеру. Уравнение применимо для представления равновесия жидкость–пар и жидкость–жидкость в многокомпонентных системах при использовании только параметров бинарного взаимодействия и данных о чистых компонентах. Кроме того, оно учитывает влияние температуры по крайней мере для среднего диапазона.
Основными недостатками уравнения UNIQUAC – это его несколько большая алгебраическая сложность, а также часто более низкая по сравнению с некоторыми менее сложными уравнениями степень точности представления данных.
В [46] было рассмотрено моделирование коэффициентов активности от концентрации раствора уравнениями локальных составов.
Уравнение UNIQUAC положено в основу метода групповых вкладов UNIFAC (Universal functional group Activity Coefficients), предназначенного для определения коэффициентов активности по данным о структуре [47].
Модель UNIFAC была предложена Фреденслундом А., Джонсом Р.Л. Праузницем Д.И. Основная идея модели «раствора групп» заключается в использовании существующих данных по фазовому равновесию для расчета фазового равновесия систем, для которых экспериментальные данные отсутствуют.
Комбинаторная часть коэффициента активности в уравнении UNIFAC такая же, как и в уравнении UNIQUAC. Остаточная часть коэффициента подсчитывается как сумма групповых вкладов:
![]() (1.69)
(1.69)
где ![]() – число групп вида k
в молекуле i
;
– число групп вида k
в молекуле i
;
![]() и
и ![]() – остаточные коэффициенты активности группы k
в растворе и чистой жидкости i
соответственно; суммирование производится по всем группам.
– остаточные коэффициенты активности группы k
в растворе и чистой жидкости i
соответственно; суммирование производится по всем группам.
Зависимость коэффициента активности ![]() от группового состава раствора описывается соотношением, аналогичным соотношениям (1.63) и (1.66).
от группового состава раствора описывается соотношением, аналогичным соотношениям (1.63) и (1.66).
![]() (1.70)
(1.70)
![]() ;
; ![]() (1.71)
(1.71)
![]() , (1.72)
, (1.72)
где ![]() – мольная доля групп m
в растворе;
– мольная доля групп m
в растворе;
![]() и
и ![]() – параметры, характеризующие взаимодействие каждой пары групп;
– параметры, характеризующие взаимодействие каждой пары групп;
![]() – мера энергии взаимодействия групп n
и m
.
– мера энергии взаимодействия групп n
и m
.
Как показали расчёты, модель UNIFAC обеспечивает точность предсказания коэффициентов активности и парожидкостного равновесия, достаточную для технологических целей. В [47] отмечается, что ошибка в значении коэффициентов активности для большинства систем не превышает 10-12%. Модель позволяет также описывать равновесие между жидкими фазами.
В [48] авторы рассматривают выбор базовых смесей для предсказания фазового равновесия по групповой модели.
В настоящее время уже рассчитаны значения групповых параметров для многих практически важных функциональных групп, поэтому для применения модели UNIFAC необходимо определить только параметры, учитывающие молекулярную структуру чистых компонентов.
1.8 Постановка задачи исследования
· Провести систематический анализ складок на поверхности равновесных температур кипения для четырехкомпонентных смесей в общем виде.
· Определить качественный ход складок на поверхности равновесных температур кипения и единичных ![]() -линий для случая экстрактивной ректификации двухфазных четырехкомпонентных смесей.
-линий для случая экстрактивной ректификации двухфазных четырехкомпонентных смесей.
· Провести расчетное исследование структуры диаграммы парожидкостного равновесия конкретной четырехкомпонентной смеси с целью получения складок первой кратности на поверхности равновесных температур кипения и единичных ![]() -линий.
-линий.