Неевклидова геометрия

СОДЕРЖАНИЕ: Происхождение Неевклидовой геометрии. Возникновение геометрии Лобачевского. Аксиоматика планиметрии Лобачевского. Три модели геометрии Лобачевского. Модель Пуанкаре и Клейна. Отображение геометрии Лобачевского на псевдосфере (интерпретация Бельтрами).

Министерство образования Российской Федерации.

Реферат.

Неевклидова геометрия.

Содержание:

1. Введение

2. Появление геометрии Лобачевского

3. Три модели геометрии Лобачевского

1) Модель Пуанкаре

2) Модель Клейна

3) Интерпретация Бельтрами

4. Свойства и понятия

5. Практическое применение геометрии Лобачевского

6. 1) Теорема Пифагора

2) Замечание к теореме Пифагора

3) Площадь треугольника

4) Длина окружности и площадь круга

7. Вывод

8. Список источников

1. Введение:

Геометрия – это одна из древнейших наук. Исследовать различные пространственные формы издавна побуждало людей их практическая деятельность. Древнегреческий ученый Эдем Родосский в IV веке до нашей эры писал: «Геометрия была открыта египтянами, и возникла при измерении Земли. Это измерение было им необходимо вследствие разлития реки Нил, постоянно смывавшей границы. Нет ничего удивительного, что эта наука, как и другие, возникла из потребности человека».

Многие первоначальные геометрические сведения получили также шумеро-вавилонские, китайские и другие ученые древнейших времен. Устанавливались они сначала только опытным путем, без логических доказательств.

Как наука, геометрия впервые сформировалась в Древней Греции, когда геометрические закономерности и зависимости, найденные ранее опытным путем, были приведены в надлежащую систему и доказаны.

В III веке до нашей эры греческий ученый Евклид привел в систему известные ему геометрические сведения в большом сочинении «Начала». Эта книга более двух тысяч лет служила учебником геометрии во всем мире.

В своём реферате я хочу показать, что кроме геометрии, которую изучают в школе (Геометрии Евклида или употребительной геометрии), существует еще одна геометрия, геометрия Лобачевского. Эта геометрия существенно отличается от евклидовой, например, в ней утверждается, что через данную точку можно провести бесконечно много прямых, параллельных данной прямой, что сумма углов треугольника меньше 180°. В геометрии Лобачевского не существует прямоугольников, подобных треугольников и так далее.

Я выбрал данную тему по нескольким причинам: теория геометрии Лобачевского помогает взглянуть по-другому на окружающий нас мир, это интересный, необычный и прогрессивный раздел современной геометрии, она дает материал для размышлений – в ней не все просто, не все ясно с первого взгляда, чтобы ее понять, нужно обладать фантазией и пространственным воображением. Ситуация с геометрией Лобачевского и геометрией Евклида во многом похожа на ситуацию с Теорией относительности Эйнштейна и классической физикой. Геометрия Лобачевского и ОТП Эйнштейна это прогрессивные взаимосвязанные теории, выполняющиеся на огромных величинах и расстояниях, и остающимися верными на приближениях к нулю. В пространственной модели ОТП используется не обычная евклидовая плоскость, а искривленное пространство, на котором верна теория Лобачевского.

Неевклидова геометрия появилась вследствие долгих попыток доказать V постулат Евклида, аксиому параллельности. Эта геометрия во многом удивительна, необычна и во многом не соответствует нашим привычным представлениям о реальном мире. Но в логическом отношении данная геометрия не уступает геометрии Евклида.

2.Происхождение Неевклидовой геометрии.

Среди аксиом Евклида была аксиома о параллельности прямых, а точнее, пятый постулат о параллельных линиях: если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которых меньше развернутого угла, то такие прямые пересекаются при достаточном продолжении с одной стороны .

В современной формулировке она говорит о существовании не более одной прямой, проходящей через данную точку вне данной прямой и параллельной этой данной прямой .

Сложность формулировки пятого постулата породила мысль о возможной зависимости его от других постулатов, и потому возникали попытки вывести его из остальных предпосылок геометрии. Все попытки заканчивались неудачей. Были попытки доказательства от противного: прийти к противоречию, предполагая верным отрицание постулата. Однако и этот путь был безуспешным.

Оказалось то, что пятый постулат не зависит от предыдущих, а значит, его можно заменить на ему эквивалентный. И в начале XIX века, почти одновременно сразу у нескольких математиков: у К. Гаусса в Германии, у Я. Больяи в Венгрии и у Н. Лобачевского в России, возникла мысль о существовании геометрии, в которой верна аксиома, заменяющая пятый постулат: на плоскости через точку, не лежащую на данной прямой, проходят, по крайней мере, две прямые, не пересекающие данную.

В силу приоритета Н. Лобачевского, который первым выступил с этой идеей в 1826, и его вклада в развитие новой, отличной от евклидовой геометрии последняя была названа в его честь «геометрией Лобачевского».

Аксиоматика планиметрии Лобачевского отличается от аксиоматики планиметрии Евклида лишь одной аксиомой: аксиома параллельности заменяется на ее отрицание – аксиому параллельности Лобачевского:

Найдутся такая прямая a и такая не лежащая на ней точка A, что через A проходят по крайней мере две прямые, не пересекающие a.

Непротиворечивость системы аксиом доказывается представлением модели, в которой реализуются данные аксиомы.

3. Три модели геометрии Лобачевского.

Выделяют три различные модели геометрии Лобачевского:

1) Модель Пуанкаре

2) Модель Клейна

3) Отображение геометрии Лобачевского на псевдосфере (интерпретация Бельтрами)

1) Модель Пуанкаре.

В модели Пуанкаре на евклидовой плоскости E фиксируется горизонтальная прямая x. Она носит название «абсолюта». Точками плоскости Лобачевского считаются точки плоскости E, лежащие выше абсолюта x. Таким образом, в модели Пуанкаре плоскость Лобачевского – это полуплоскость L, лежащая выше абсолюта.

Прямыми плоскости L считаются полуокружности с центрами на абсолюте или лучи с вершинами на абсолюте и перпендикулярные ему.

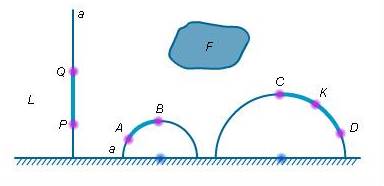Фигура на плоскости Лобачевского – это фигура полуплоскости L. Принадлежность точки фигуре понимается так же, как и на евклидовой плоскости E. При этом отрезком плоскости L считается дуга окружности с центром на абсолюте или отрезок прямой, перпендикулярной абсолюту (рис. 1 ). Точка K лежит между точками C и D, значит, что K принадлежит дуге CD. В условиях нашей модели это эквивалентно тому, что K лежит между C и D, где C, K и D – проекции точек C, K и D соответственно на абсолют. Чтобы ввести понятие равенства неевклидовых отрезков в модели Пуанкаре, определяют неевклидовы движения в этой модели. Неевклидовым движением называется преобразование L, которое является композицией конечного числа инверсий с центрами на абсолюте и осевых симметрий плоскости E, оси которых перпендикулярны абсолюту. Инверсии с центром на абсолюте и осевые симметрии

Рисунок 1 плоскости E, оси которых перпендикулярны абсолюту, называют неевклидовыми симметриями. Два неевклидовых отрезка называют равными, если один из них неевклидовым движением можно перевести во второй.

2) Модель Клейна.

За плоскость принимается какой-либо круг (рис. 2.1 ), за точки - точки принадлежащие этому кругу, за прямые - хорды - конечно, с исключением концов, поскольку рассматривается только внутренность круга. За перемещения принимаются преобразования круга, переводящие его в себя и хорды - в хорды. Соответственно, конгруэнтными называются фигуры, переводимые друг в друга такими преобразованиями.

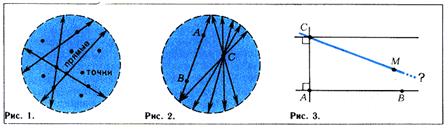
Рисунок 2

Очевидно, что в пределах определенной части плоскости (круга), как бы эта часть не была велика, можно провести через данную точку С множество прямых, не пересекающих данной прямой. Внутри круга любого конечного радиуса существует множество прямых (т.е. хорд), проходящих через т. С и не встречающих прямой АВ (рис.2.2 ). Всякая теорема планиметрии Лобачевского является в этой модели теоремой геометрии Евклида и, обратно, всякая теорема геометрии Евклида, говорящая о фигурах внутри данного круга, является теоремой геометрии Лобачевского. Это общее утверждение доказывается проверкой справедливости в модели аксиом геометрии Лобачевского. Поэтому, если в геометрии Лобачевского имеется противоречие, то это же противоречие имеется и в геометрии Евклида.

Далее, всякая теорема геометрии Лобачевского описывает в модели Клейна некоторые факты, имеющие место внутри круга. Именно факты, если мы берем не абстрактный круг, а реальный круг и реальные хорды и интерпритируем теоремы как утверждения об этих реальных вещах, взятые, конечно, с той точностью, которая доступна для наших построений. Таким образом, геометрия Лобачевского в модели Клейна имеет вполне реальный смысл с той точностью, с какой вообще имеет смысл геометрия в применении к реальным телам.

3) Отображение геометрии Лобачевского на псевдосфере (интерпретация Бельтрами)

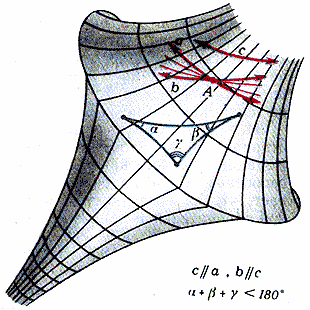
Эудженио Бельтрами (1835-1900) нашел модель для неевклидовой геометрии, показав в своей работе «Опыт интерпретации неевклидовой геометрии» (1868г.), что наряду с плоскостями, на которых осуществляется евклидова геометрия, и сферическими поверхностями, на которые действуют формулы сферической геометрии, существуют и такие реальные поверхности, названные им псевдосферами (рис.4 ), на которых частично осуществляется планиметрия Лобачевского.

Известно, что сферу можно получить вращением полуокружности вокруг своего диаметра. Подобно тому, псевдосфера образуется вращением линии FCE, называемой трактрисой, вокруг ее оси АВ (рис.3 ). Итак, псевдосфера – это поверхность в обыкновенном реальном пространстве, на котором выполняются многие аксиомы и теоремы неевклидовой планиметрии Лобачевского. Например, если начертить на псевдосфере треугольник, то легко усмотреть, что сумма его внутренних углов меньше 2. Сторона треугольника – это дуги псевдосферы, дающие кратчайшее расстояние между двумя ее точками и выполняющие ту же роль, которую выполняют прямые на плоскости. Эти линии, называемые геодезическими, можно получить, зажав туго натянутую и политую краской или мелом нить, в вершинах треугольника. Таким образом, для планиметрии Лобачевского была найдена реальная модель - псевдосфера. Формулы новой геометрии Лобачевского нашли конкретное истолкование. Ими можно было пользоваться, например, для решения псевдосферических треугольников. Псевдосферу, которую мы назвали «моделью», Бельтрами назвал интерпретацией (истолкованием) неевклидовой геометрии на плоскости.

Впоследствии, с развитием и введением в математику аксиоматического метода, под

Рисунок 4 интерпретацией (или моделью) некоторой системы аксиом стали понимать любое множество объектов, в которых данная система аксиом находит свое реальное воплощение, то есть, любая совокупность объектов, отношение между которыми полностью совпадают с теми, которые описываются в данной системе аксиом. При этом полагают, что если для некоторой системы аксиом существует или можно построить интерпретацию (модель), то эта система аксиом непротиворечива, то есть, не только сами аксиомы, но и любые теоремы, на них логически основывающиеся никогда не могут противоречить одна другой.

4. Свойства и понятия.

Рассмотрим некоторые свойства, понятия и факты выполняющиеся в геометрии Лобачевского. В данном случае я рассматривал свойства основываясь на модели Клейна. Большинство из них будут выполнятся и на других моделях неевклидовой геометрии.

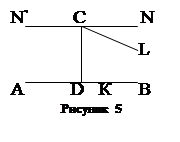1) Если прямые CN и CL не встречают прямой АВ, то любая прямая СМ, проходящая через т. C внутри вертикальных углов NCL и N’CL’ также не встретит прямой АВ (рис.5). Отсюда первое следствие аксиомы Лобачевского: через т. С вне прямой АВ плоскости АВС, проходит бесчисленное множество прямых, не пересекающихся с прямой АВ.

2) Если соединить (рис.5 ) какую-либо точку прямой DB с т. С, получим прямую, допустим, СК, проходящую через т. С и встречающую АВ. Итак, все прямые, проходящие через т. С внутри прямого угла NCD, разбиваются на две категории, на два класса: встречающие прямую АВ (названные Лобачевским «сходящимися» с АВ) и не встречающие прямую АВ (их Лобачевский называет «расходящимися» с АВ). Любая прямая первой категории образует с перпендикуляром CD угол, меньший угла, образованного перпендикуляром CD с любой прямой второй категории. Вращаясь непрерывно около т. С в направлении против часовой стрелки, прямая СК на известном этапе, допустим в положении CL, перестанет пересекать АВ и из сходящейся перейдет в категорию расходящихся с АВ прямых. Эта предельная прямая CL, служащая переходной прямой, граничной, отделяющей сходящиеся от расходящихся прямых, и названной Лобачевским параллельной к прямой АВ из т. С. Итак, параллельная CL – это не просто расходящаяся прямая, а первая, граничная расходящаяся, т.е. такая, что любая прямая, проходящая через т. С внутри угла, образованного параллельной CL и перпендикуляром CD, является сходящейся прямой, а всякая прямая, проходящая внутри угла LCN будет расходящаяся с прямой АВ. Угол DCL, образованный параллельной CL с перпендикуляром CD, называют углом параллельности.

В силу симметрии относительно перпендикуляра CD внутри прямого угла N’CD получим картину, аналогично той, которую мы имеем в угле NCD, т.е. построив угол DCF равный углу DCL, получим прямую CF, также параллельную прямой АВ слева от перпендикуляра CD. Итак, через т. С, лежащую вне прямой АВ, проходят в плоскости АВС две прямые, параллельные прямой АВ, в одну и другую сторону этой прямой. Все прямые, проходящие внутри вертикальных углов, образованных параллельными прямыми LL’ и GG’ (в том числе и евклидова «параллельная» NN’), расходятся с АВ; все остальные прямые, проходящие через т. С сходятся с прямой АВ.

Следовательно: а) 2 прямые как АВ и NN’, имеющие общий перпендикуляр CD, расходятся; б) если вращать прямую NN’ около т. С, допустим, по часовой стрелке, а прямую АВ около т.D в том же направлении так, чтобы углы, образованные этими прямыми с пересекающей их прямой CD, оставались равными, то прямые АВ и NN’ остаются расходящимися, т.е. две прямые, образующие при пересечении с третьей прямой равные соответственные углы, расходятся.

3) Из предыдущего положения вытекает, что на параллели Лобачевского различается направление параллельности. Прямая CE параллельна прямой АВ в направлении или в сторону от A к B, прямая CF параллельна той же прямой AB в направлении или в сторону ВА (от В к А) (рис.5).

Несмотря на коренные отличия, понятия параллельности у Лобачевского от одновременного понятия в геометрии Евклида, можно доказать, что «параллельность» в смысле Лобачевского тоже обладает свойствами взаимности или симметрии (если прямая а параллельна прямой в , то в параллельна а ). И транзитивности (если а и в параллельны с , то а и в параллельны между собой).

Приведем некоторые другие понятия и факты геометрии Лобачевского:

1) Функция Лобачевского.

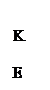Как уже говорилось выше, через т. С в плоскости САВ проходят 2 направленные параллели к прямой АВ (СЕ и CF), симметрично расположенные относительно перпендикуляра CD (рис.6 ). Угол параллельности, образованный каждой из этих параллелей с CD, является острым, его величина не постоянна и зависит от расстояния CD(в геометрии Евклида угол параллельности всегда прямой). То, что угол параллельности острый, вытекает непосредственно из аксиомы Лобачевского. В изменении этого угла с изменением расстояния CD можно убедиться путем следующих рассуждений (рис.7 ).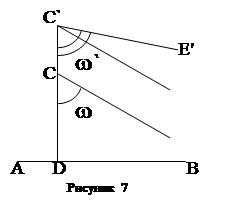 Пусть C’DCD, CE || AB, в т. С угол параллельности – W. Пусть далее прямая C’E ‘|| AB в т. С’ угол параллельности - W’. В силу свойства транзитивности CE||C’E’. Ясно, что WW’. Действительно, если допустить, что W= W’, то следует также допустить, что C’E’ и CE – расходящиеся прямые, как было показано выше, а это неверно. Построим C’K, образующую с CD угол a= w, ясно, что w’ a , т.к. параллельC’E’ ближе к перпендикуляру, чем расходящаяся C’K. Итак, w w ; отсюда следует, что угол параллельности убывает по мере удаления от прямой АВ; чем ближе т. С к прямой АВ, т.е. чем короче перпендикуляр CD, тем больше угол параллельности. Если обозначить расстояние т. С от прямой АВ, т.е. длину перпендикуляра CD через х, то можно сказать, что угол параллельности есть функция от х, названная «функцией Лобачевского» и обозначаемая П (х). Это монотонно убывающая функция. При изменении аргумента х от 0 до функция П (х) непрерывно изменяется соответственно от p /2 до 0. Таким образом,

,

При х ® 0 , иными словами, если оставаться в пределах сравнительно небольших расстояний, то угол параллельности мало отличается от p /2 то есть от этого значения, которое он имеет в евклидовой геометрии, это означает, что геометрия Лобачевского не противоречит, не исключает геометрии Евклида; последнего можно рассматривать как частный случай большой общей геометрии – геометрии Лобачевского. Реальный смысл предельного перехода (при х ® 0) от геометрии Лобачевского к геометрии Евклида состоит в том, что физика изучает, в конечном счете, только ограниченную, сравнительно небольшую часть пространства. Вот почему в окружающей нас среде (даже в пределах нашей планеты) свойства физического пространства приблизительно таковы, какими мы их знаем из Евклидовой геометрии, но для всего пространства, для мира звезд, для вселенной в целом, они иные, неевклидовы.

2) Сумма углов треугольника меньше 2 .

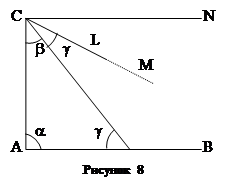
Это предположение эквивалентно аксиоме Лобачевского, то есть из него вытекает эта аксиома и наоборот. Для примера докажем первое. Пусть (рис.8 ) в прямоугольном треугольнике CDK сумма углов S= a+b+g2, то есть b+g.Это значит, что внутри угла NCK можно построить LCK = а (NC^CD).

Прямая CL не может пересечь прямой АВ в какой- либо точке М, так как если бы это случилось, то угол DKC , внешний по отношению к треугольнику KCM , равнялся бы внутреннему, не смежному с ним углу треугольника KCM, что противоречит абсолютной геометрии о внешнем угле треугольника. Итак, через т. С, кроме CN , проходит еще одна прямая – CL, не встречающая прямой АВ; следовательно, верна аксиома Лобачевского. Разность (2–S), то есть между 180 и суммой углов данного треугольника, называется угловым дефектом этого треугольника.

3) Предложение «сумма углов четырехугольника меньше 4» вытекает из предыдущего. Отсюда следует, что в геометрии Лобачевского нет ни прямоугольников, ни квадратов. Вообще сумма углов n – угольника меньше 2(n-2).

4) Внешний угол треугольника больше суммы внутренних, с ним не смежных углов. Действительно, пусть d - внешний угол треугольника, смежный с внутренним углом треугольника a , и пусть b и g - остальные его внутренние углы, тогда: a + d = 2.

Следует, что d b + g .

5) Если три угла одного треугольника соответственно равны трем углам другого треугольника, то эти треугольники равны между собой. Это четвертый признак равенства треугольников в геометрии Лобачевского.

Таким образом, в плоскости Лобачевского треугольник вполне определяется своими углами. Стороны и углы зависят друг от друга. Отсюда ясно, что в геометрии Лобачевского нет подобных фигур. Действительно, ведь из существования подобных фигур вытекает евклидова аксиома параллельности.

6) Площади . Уже известно, что, чем меньше размеры фигур, которые мы изучаем, тем ближе к геометрии Евклида, в которой угловой дефект треугольника равен 0. Доказывается следующая теорема: площадь треугольника прямопропорциональна его угловому дефекту. Чем меньше размеры фигуры, тем меньше ее дефект, тем меньше площадь. Однако угловой дефект по определениям не может превзойти 2, следовательно, и площадь треугольника в геометрии Лобачевского не может стать больше некоторой, определенной, конечной величины.

5. Практическое применение геометрии Лобачевского.

1) Теорема Пифагора.

Теорема . Для всякого прямоугольного треугольника плоскости Лобачевского выполняется равенство ch c = ch a ·ch b, где a, b - длины катетов, c - длина гипотенузы этого треугольника, а ch x =(гиперболический косинус).

Доказательство. Воспользуемся моделью Пуанкаре плоскости Лобачевского на евклидовой полуплоскости. Будем считать (см. рисунок ниже), что вершинам A, B, C данного прямоугольного треугольника соответствуют комплексные числа где так как этого всегда можно добиться с помощью некоторого неевклидова движения.

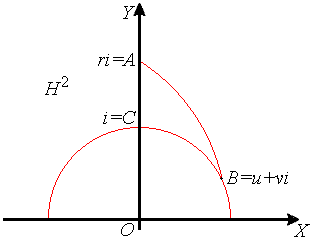
Используя формулу

для вычисления неевклидова расстояния между точками z и w в H² , получаем, что

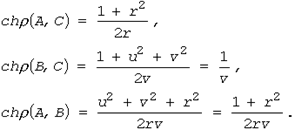
Почленное перемножение двух первых соотношений и приводит, как показывает третье соотношение, к завершению доказательства теоремы.

2) Замечание к теореме Пифагора

Н.И.Лобачевским было замечено, что созданная им неевклидова геометрия в бесконечно малом, то есть в первом приближении, совпадает с геометрией евклидовой плоскости. Проиллюстрируем это на примере теоремы Пифагора. Используя разложение гиперболического косинуса в ряд

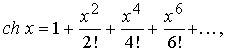
получим для теоремы Пифагора соотношение

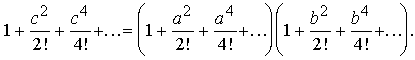
Исключая теперь члены низшего порядка, приходим к теореме Пифагора евклидовой геометрии:

3) Площадь треугольника

Подробный вывод формулы площади треугольника на плоскости Лобачевского я приводить не буду ввиду его сложности (в нем используется формулы, доказываемые лишь в курсе дифференциальной геометрии).

Если ABC - треугольник в модели Пуанкаре, меры углов A, B и C - , и соответственно, - мера угла B в треугольнике ABD, а 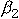и 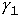мера углов B и C в треугольнике BCD. Тогда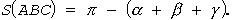

Вследствие этого можно сформулировать теорему

Теорема. Для площади треугольника ABC с угламисправедлива формула

Следствие1. Площадь треугольника плоскости Лобачевского ограничена.

Следствие 2. Если дан выпуклый многоугольник с внутренними углами ^то

4) Длина окружности и площадь круга.

Теорема. Площадь круга с радиусом r равна

а длина окружности, ограничивающей этот круг, равна , где . Длина неевклидовой окружности не пропорциональна радиусу, как в случае евклидовой геометрии, а растет быстрее. Также площадь неевклидова круга больше площади круга евклидовой плоскости, имеющего тот же радиус.

6. Вывод:

Открытие неевклидовой геометрии, начало которому положил Лобачевский, не только сыграло огромную роль в развитии новых идей и методов в математике естествознании, но имеет и философское значение. Господствовавшее до Лобачевского мнение о незыблемости геометрии Евклида в значительной мере основывалось на учении известного немецкого философа И. Канта (1724-1804), родоначальника немецкого классического идеализма. Кант утверждал, что человек упорядочивает явления реального мира согласно априорным представлениям, а геометрические представления и идеи якобы априорны (латинское слово aprior означает – изначально, заранее), то есть, не отражают явлений действительного мира, не зависят от практики, от опыта, а являются врожденными человеческому миру, раз и навсегда зафиксированными, свойственными человеческому разуму, его духу. Поэтому, Кант считал, что Евклидова геометрия непоколебима, неизменна, и является вечной истиной. Еще до Канта геометрия Евклида считалась незыблемой, как единственно возможное учение о реальном пространстве.

Открытие неевклидовой геометрии доказало, что нельзя абсолютировать представления о пространстве, что «употребительная» (как назвал Лобачевский геометрию Евклида) геометрия не является единственно возможной, однако это не подорвало незыблемость геометрии Евклида. Итак, в основе геометрии Евклида лежат не априорные, врожденные уму понятия и аксиомы, а такие понятия, которые связаны с деятельностью человека, с человеческой практикой. Только практика может решить вопрос о том, какая геометрия вернее излагает свойства физического пространства. Открытие неевклидовой геометрии дало решающий толчок грандиозному развитию науки, способствовало и поныне способствует более глубокому пониманию окружающего нас материального мира.

Список источников:

1. Математика XIX века, «Наука», М., 1981

2. “Квант” №11,№12 Академик АН СССР А.Д. Александров, Интернет-издания.

3. Юшкевич А.П., История математики в России, «Наука», М., 1968

4. Ефимов Н.В., Высшая геометрия, «Наука», М.,1971.

5. Неевклидовы пространства и новые проблемы физики, «Белка», М., 1993

6. Клайн М., Математика. Утрата определенности, «Мир», М., 1984

7. Г.И. Глейзер. История математики в школе IX – X классы. Пособие для учителей. Москва, «Просвещение» 1983г.

8. Даан Дальмедино А., Пейффер И. Пути и лабиринты. Очерки по истории математики. Перевод с французского. М: Мир.1986г.

9. Б.Л. Лаптев. Н.И. Лобачевский и его геометрия. Пособие для учащихся. М. «Просвещение», 1970г.

10. И.М. Яглам. Принцип относительности Галилея и неевклидова геометрия. Серия «Библиотека математического кружка» М: 1963г.

11. http://www.bankreferatov.ru

12. http://www.refportal.ru

13. http://www.edu.ru

14. http://www.

15. http://www.themesoch.narod.ru/t_s

16. http://www.referat.online.ru

17. http://www.pautina.net

Скачать архив с текстом документа