Некоторые линейные операторы
СОДЕРЖАНИЕ: Содержание Введение §1. Определение линейного оператора. Примеры §2. Непрерывные линейные операторы в нормированном пространстве. Ограниченность и норма линейного оператораСодержание
Введение
§1. Определение линейного оператора. Примеры
§2. Непрерывные линейные операторы в нормированном пространстве. Ограниченность и норма линейного оператора
§3. Обратный оператор. Спектр оператора и резольвента
§4. Оператор умножения на непрерывную функцию
§5. Оператор интегрирования
§6. Оператор дифференцирования
§7. Оператор сдвига
Заключение
Введение
Наиболее доступными для изучения среде операторов, действующих в линейных нормированных пространствах, являются линейные операторы. Они представляют собой достаточно важный класс операторов, так как среди них можно найти операторы алгебры и анализа.
Целью дипломной работы является показать некоторые из линейных операторов, исследовать их на непрерывность и ограниченность, найти норму ограниченного оператора, а также спектр оператора и его резольвенту.
В первом и втором параграфах приведены основные сведения теории операторов: определение линейного оператора, непрерывности и ограниченности линейного оператора, его нормы. Рассмотрены некоторые примеры.
В третьем параграфе даны определения обратного оператора, спектра оператора и его резольвенты. Рассмотрены примеры.
В четвертом параграфе исследуется оператор умножения на непрерывную функцию: Ах(t) = g(t)x(t).
В пятом параграфе приведен пример оператора интегрирования Аf(t)=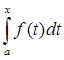 .
.
В седьмом параграфе исследуется оператор сдвига Af(x) = f(x+a).
Показана линейность, непрерывность, ограниченность, найдена норма, точки спектра и резольвента всех трех операторов.
В шестом параграфе исследуется оператор дифференцирования Дf(x)=f/ (x), в пространстве дифференцируемых функции D[ a , b ] . Показана его линейность. Доказано, что Д не является непрерывным оператором, а также как из неограниченности оператора следует его разрывность.
§1. Определение линейного оператора. Примеры
Определение 1.
Пусть Ex
и Ey
[1]
– линейные пространства над полем комплексных (или действительных) чисел. Отображение А: Ex
® Ey
называется линейным оператором
, если для любых элементов х1
и х2
пространства Ex
и любого комплексного (действительного) числа ![]() выполняются следующие равенства [2]
:
выполняются следующие равенства [2]
:
1. А(х1 +х2 ) = Ах1 + Ах2 ;
2. А(![]() х) =
х) = ![]() А(х);
А(х);
Примеры линейных операторов:
1) Пусть Е = Е1 – линейное топологическое пространство. Оператор А задан формулой:
Ax = x для всех x ![]() Е.
Е.
Такой оператор, переводящий каждый элемент пространства в себя является линейным и называется единичным оператором.
2) Рассмотрим D[ a , b ] – пространство дифференцируемых функций, оператор дифференцирования Д в пространстве D[ a , b ] задан формулой:
Дf(x) = f/ (x).
Где f(x) ![]() D[a, b]
, f/
(x)
D[a, b]
, f/
(x) ![]() C[a, b]
.
C[a, b]
.
Оператор Д определен не на всем пространстве C[ a , b ] , а лишь на множестве функций имеющих непрерывную производную. Его линейность, очевидно, следует из свойств производной.
3) Рассмотрим пространство С[-![]() , +
, +![]() ]
– пространство непрерывных и ограниченных функций, оператор А сдвигает функцию на const a:
]
– пространство непрерывных и ограниченных функций, оператор А сдвигает функцию на const a:
Аf(x) = f(x+a).
Проверим линейность оператора А:
1) А(f+g) = (f+g)(x+a) = f(x+a) + g(x+a) = А(f) + А(g).
Исходя из определения суммы функции, аксиома аддитивности выполняется.
2) A(kf(x)) = kf(x+a) = kA(f(x)).
Верна аксиома однородности.
Можно сделать вывод, что А – линейный оператор.
4) Пусть ![]()
![]()
![]() (пространство непрерывных функций на отрезке [0,1], и дано отображение
(пространство непрерывных функций на отрезке [0,1], и дано отображение ![]() 1
, заданное формулой:
1
, заданное формулой:
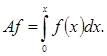
Так как интеграл с переменным верхним пределом от непрерывной функции является функцией дифференцируемой, а, следовательно, непрерывной, то ![]()
![]() . В силу линейности определенного интеграла данное отображение является линейным оператором.
. В силу линейности определенного интеграла данное отображение является линейным оператором.
§2. Непрерывные линейные операторы в нормированном
пространстве. Ограниченность и норма линейного оператора
Пусть ![]() ,
, ![]() – нормированные пространства.
– нормированные пространства.
Определение 2 .
Оператор А: Е ![]() Е1
называется непрерывным
в точке
Е1
называется непрерывным
в точке ![]() , если какова бы не была последовательность xn
, если какова бы не была последовательность xn
![]() x0
, А(xn
) сходится к А(x0
). То есть, при p (xn
, x0
)
x0
, А(xn
) сходится к А(x0
). То есть, при p (xn
, x0
) ![]() 0, p (А(xn
), А(x0
))
0, p (А(xn
), А(x0
)) ![]() 0.
0.
Известно и другое (равносильное) определение непрерывности линейного оператора.
Определение 3.
Отображение А называется непрерывным
в точке x0
, если какова бы не была окрестность[3]
U точки y0
= А (x0
) можно указать окрестность V точки x0
такую, что А(V) ![]() U.
U.
Иначе ![]() 0
0 ![]() 0, что как только p (x, x0
)
0, что как только p (x, x0
) ![]() , p (f(x), f(x0
))
, p (f(x), f(x0
)) ![]() .
.
Теорема 1.
Если линейный оператор непрерывен в точке х0 = 0, то он непрерывен и в любой другой точке этого пространства.
Доказательство.
Линейный оператор А непрерывен в точке х0
=0 тогда и только тогда, когда ![]() . Пусть оператор А непрерывен в точке х0
=0. Возьмем последовательность точек пространства хn
®х1
, тогда хn
–х1
®0, отсюда А(хn
–х1
)®А(0)=0, т. е. А(хn
–х1
)®0.
. Пусть оператор А непрерывен в точке х0
=0. Возьмем последовательность точек пространства хn
®х1
, тогда хn
–х1
®0, отсюда А(хn
–х1
)®А(0)=0, т. е. А(хn
–х1
)®0.
Так как А – это линейный оператор, то А(хn –х1 )®Ахn –Ах0 , а тогда
Ахn -Ах0 ® 0, или Ахn ®Ах0 .
Таким образом, из того, что линейный оператор А непрерывен в точке х0 =0, следует непрерывность в любой другой точке пространства.
т. д-на.
Пример.
Пусть задано отображение F(y) = y(1) пространства С[0, 1] в R. Проверим, является ли это отображение непрерывным.
Решение.
Пусть y(x) – произвольный элемент пространства С[0, 1] и yn (x) – произвольная сходящаяся к нему последовательность. Это означает:
![]() p (yn
, y) =
p (yn
, y) = ![]()
![]() |yn
(x)- y(x))| = 0.
|yn
(x)- y(x))| = 0.
Рассмотрим последовательность образов: F(yn ) = yn (1).
Расстояние в R определено следующим образом:
p (F(yn
), F(y)) = |F(yn
) - F(y))| = | yn
(1) - y(1)| ![]()
![]() |yn
(x)- y(x))|=p(yn
,y),
|yn
(x)- y(x))|=p(yn
,y),
то есть p (F(yn
), F(y)) ![]() 0.
0.
Таким образом, F непрерывно в любой точке пространства С[ a , b ] , то есть непрерывно на всем пространстве.
С понятием непрерывности линейного оператора тесно связано понятие ограниченности.
Определение 4.
Линейный оператор А: Е ![]() Е1
называется ограниченным
, если можно указать число K0 такое, что
Е1
называется ограниченным
, если можно указать число K0 такое, что
||Аx|| ![]() K||x||. (1)
K||x||. (1)
Теорема 2.
Среди всех констант K, удовлетворяющих (1), имеется наименьшее.
Доказательство:
Пусть множество S – множество всех констант K, удовлетворяющих (1), будучи ограниченным снизу (числом 0), имеет нижнюю грань k. Достаточно показать, что k ![]() S.
S.
По свойству нижней грани в S можно указать последовательность (kn
), сходящуюся к k. Так как kn
![]() S, то выполняется неравенство: |А(x)|
S, то выполняется неравенство: |А(x)| ![]() kn
||x||, (x
kn
||x||, (x![]() E). Переходя в этом неравенстве к пределу
E). Переходя в этом неравенстве к пределу
![]()
получаем |А(x)| ![]() k||x||, где (x
k||x||, где (x![]() E), (k
E), (k ![]() S).
S).
т. д-на.
Определение 5. Наименьшая из этих констант K, для которых выполняется неравенство (1), называется нормой оператора А и обозначается ||A||[4] .
||А|| ![]() K, для
K, для ![]() K, подходящего для (1), то есть |А(x)|
K, подходящего для (1), то есть |А(x)| ![]() ||А||||x||, где
||А||||x||, где
||А|| = ![]()
![]() x
x![]() E.
E.
Между ограниченностью и непрерывностью линейного оператора существует тесная связь, а именно справедлива следующая теорема.
Теорема 3.
Для того, чтобы линейный оператор А действующий из Ex в Ey был ограничен, необходимо и достаточно, чтобы оператор А был непрерывен.
Необходимость :
Дано: А – ограничен;
Доказать: А – непрерывен;
Доказательство:
Используя теорему 1 достаточно доказать непрерывность А в нуле.
Дано, что ||Аx|| ![]() K||x||.
K||x||.
Докажем, что А непрерывен в нуле, для этого должно выполняться ![]() 0,
0, ![]() 0 что ||x||
0 что ||x|| ![]()
![]() ||Ax||
||Ax|| ![]() .
.
Выберем ![]() так, чтобы K*||x||
так, чтобы K*||x|| ![]() , ||x||
, ||x|| ![]() , (К0), значит
, (К0), значит ![]() =
= ![]() , тогда если ||x||
, тогда если ||x|| ![]() , то ||Аx||
, то ||Аx|| ![]() K||x|| K
K||x|| K![]() =
= ![]()
Непрерывность в нуле доказана, следовательно доказана непрерывность в ![]() точке.
точке.
Достаточность :
Дано: А – непрерывен;
Доказать А – ограничен;
Доказательство:
Допустим, что А не ограничен. Это значит, что числу 1 найдется хотя бы один соответственный вектор x1 такой, что ||A x1 || 1|| x1 ||.
Числу 2 найдется вектор x2 , что ||A x2 || 2|| x2 || и т.д.
Числу n найдется вектор xn , что ||A xn || n|| xn ||.
Теперь рассмотрим последовательность векторов yn
= ![]() , где
, где
||yn
|| = ![]() .
.
Следовательно последовательность yn
![]() 0 при n
0 при n ![]()
![]() .
.
Так как оператор А непрерывен в нуле, то Аyn
![]() 0, однако
0, однако
||Аyn
|| = ||A![]() || =
|| = ![]() ||Axn
||
||Axn
||![]() n|| xn
||
n|| xn
||![]()
![]() = 1, получаем противоречие с Аyn
= 1, получаем противоречие с Аyn
![]() 0, то есть А – ограничен
0, то есть А – ограничен
Для линейных операторов ограниченность и непрерывность оператора эквивалентны.
Примеры.
1) Покажем, что норма функционала[5]
F(y) = 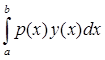 в C[
a
,
b
]
, где p(x) – непрерывная на [a,b] функция, равна
в C[
a
,
b
]
, где p(x) – непрерывная на [a,b] функция, равна 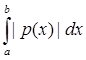 .
.
По определению 5: ||F|| = ![]() |F(x)| =
|F(x)| = ![]() |
|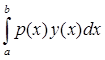 |.
|.
|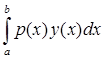 |
| ![]() |
|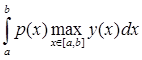 | = |
| = |![]() y(x)||
y(x)||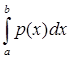 |
| ![]()
![]() |y(x)||
|y(x)|| |;
|;
||F|| = ![]() (
(![]() |y(x)||
|y(x)||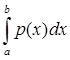 |) =
|) = ![]() ||y(x)|||
||y(x)|||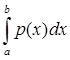 | = |
| = |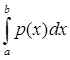 |
| ![]()
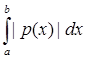 .
.
Таким образом, норма F(y) = 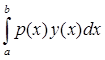 будет ||F|| =
будет ||F|| = 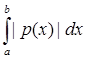 ;
;
2) Найдем норму функционала, определенного на C[0, 2], где p(x)=(x-1)
F(y) = 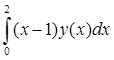 .
.
По выше доказанному ||F|| = 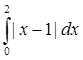 = 1.
= 1.
§3. Обратный оператор. Спектр оператора и резольвента
Пусть ![]() ,
, ![]() – нормированные пространства,
– нормированные пространства, ![]() – линейный оператор, DA
- область определения оператора,
а RA
– область значений.
– линейный оператор, DA
- область определения оператора,
а RA
– область значений.
Определение 6. Оператор А называется обратимым , если для любого элемента у, принадлежащего RA , уравнение Ах=у имеет единственное решение.
Если оператор А обратим, то каждому элементу у, принадлежащему RA , можно поставить в соответствие единственный элемент х, принадлежащий DA и являющийся решением уравнения Ах=у. Оператор, осуществляющий это соответствие, называется обратным оператором к оператору А и обозначается А-1 .
Теорема 4.
Для того чтобы линейный оператор ![]() имел ограниченный обратный оператор необходимо и достаточно, чтобы выполнялось неравенство:
имел ограниченный обратный оператор необходимо и достаточно, чтобы выполнялось неравенство:
![]() , (m0).
, (m0).
Доказательство:
Достаточность.
Пусть выполняется данное неравенство. Тогда равенство Ax=0 возможно лишь тогда, когда x – нулевой вектор. Получим 0 ![]() m*||x||, отсюда ||x||
m*||x||, отсюда ||x|| ![]() 0, но так как норма не может быть 0, то x=0. А обращается в ноль лишь на нулевом векторе. Итак, А-1
существует.
0, но так как норма не может быть 0, то x=0. А обращается в ноль лишь на нулевом векторе. Итак, А-1
существует.
Докажем его ограниченность.
y=Ax.
x=A-1
y, норма ||A-1
y||=||x||, но ||x|| ![]()
![]() ||Ax||=
||Ax||=![]() ||y||.
||y||.
Отсюда ||A-1
y|| ![]()
![]() ||y||, то есть обратный оператор существует и он ограничен.
||y||, то есть обратный оператор существует и он ограничен.
Если за m возьмем наибольшую из возможных, то получим, что ||A-1
||=![]() .
.
Необходимость.
Пусть от А имеется ограниченный обратный А-1 на нормированном пространстве.
Итак, ||A-1
y|| ![]() М||y||.
М||y||.
Подставляем значение y и значение A-1
y,получим ||x|| ![]() M||Ax|| (М всегда можно считать положительным числом).
M||Ax|| (М всегда можно считать положительным числом).
Отсюда ||Ax|| ![]()
![]() ||x||.
||x||.
Положим ![]() =m, получим ||Ax||
=m, получим ||Ax|| ![]() m||x||.
m||x||.
т. д-на.
В теории операторов важную роль играет понятие спектра оператора. Рассмотрим это понятие сначала для конечномерного пространства.
Определение 7.
Пусть А – линейный оператор в n-мерном пространстве Еn
. Число называется собственным значением
оператора А, если уравнение Ах=х имеет ненулевые решения. Совокупность всех собственных значений называется спектром
оператора А, а все остальные значения – регулярными.
Иначе говоря, есть регулярная точка, если оператор ![]() , где I – единичный оператор, обратим, При этом оператор (А – I)-1
, как и всякий оператор в конечномерном пространстве, ограничен. Итак, в конечномерном пространстве существуют две возможности:
, где I – единичный оператор, обратим, При этом оператор (А – I)-1
, как и всякий оператор в конечномерном пространстве, ограничен. Итак, в конечномерном пространстве существуют две возможности:
1) уравнение Ах=х имеет ненулевое решение, то есть является собственным значением для оператора А; оператор (А – I)-1 при этом не существует;
2) существует ограниченный оператор (А – I)-1 , то есть есть регулярная точка.
В бесконечном пространстве имеется еще и третья возможность, а именно:
3) оператор (А – I)-1 существует, то есть уравнение Ах=х имеет лишь нулевое решение, но этот оператор не ограничен.
Введем следующую терминологию. Число мы назовем регулярным для оператора А, действующего в линейном нормированном пространстве Е, если оператор (А – I)-1 , называемый резольвентой оператора А, определен на всем пространстве Е и непрерывен. Совокупность всех остальных значений называется спектром оператора А. Спектру принадлежат все собственные значения оператора А, так как, если (А – I)х=0 при некотором х0, то оператор (А – I)-1 не существует. Их совокупность называется точечным спектром . Остальная часть спектра, то есть совокупность тех , для которых (А – I)-1 существует, но не непрерывен, называется непрерывным спектром. Итак, каждое значение является для оператора А или регулярным, или собственным значением, или точкой непрерывного спектра. Возможность наличия у оператора непрерывного спектра – существенное отличие теории операторов в бесконечномерном пространстве от конечномерного случая.
Определение 8.
Оператор ![]() , где
, где ![]() – регулярная точка оператора А, называется резольвентой[6]
оператора А и обозначается
– регулярная точка оператора А, называется резольвентой[6]
оператора А и обозначается ![]() (или
(или ![]() ).
).
Теорема 5.
Пусть ![]() – линейный непрерывный оператор,
– линейный непрерывный оператор, ![]() его регулярные числа. Тогда
его регулярные числа. Тогда ![]() .
.
Доказательство.
Умножим обе части равенства на ![]() :
: ![]() (
(![]()
![]()
![]()
![]()
![]() =
=![]()
![]() =
=![]()
![]() . С другой стороны получим
. С другой стороны получим ![]()
![]()
![]() . Так как числа
. Так как числа ![]() – регулярные для оператора А, то оператор
– регулярные для оператора А, то оператор ![]() имеет обратный. Значит, из равенства
имеет обратный. Значит, из равенства ![]()
![]() следует, что
следует, что ![]() . Значит, утверждение теоремы верно.
. Значит, утверждение теоремы верно.
т. д-на.
Примеры.
1) Рассмотрим в пространстве C[0,1] оператор умножения на независимую переменную t: Ax = tx(t).
Уравнение Аx=![]() x принимает в этом случае вид:
x принимает в этом случае вид:
tx(t) - ![]() x(t) = y(t),
x(t) = y(t),
решение x(t) этого уравнения есть функция, тождественно ему удовлетворяющая.
Если ![]() лежит вне отрезка [0, 1], то уравнение Аx=
лежит вне отрезка [0, 1], то уравнение Аx=![]() x имеет при любом y(t) единственное непрерывное решение:
x имеет при любом y(t) единственное непрерывное решение:
x(t) = ![]() y(t),
y(t),
откуда следует, что все такие значения параметра ![]() являются регулярными, и резольвента есть оператор умножения на
являются регулярными, и резольвента есть оператор умножения на ![]() :
:
R![]() (y) =
(y) = ![]() y(t).
y(t).
Все значения параметра, принадлежащие отрезку[0, 1], являются точками спектра. В самом деле, пусть ![]() 0
0
![]() [0, 1]. Возьмем в качестве y(t) какую-нибудь функцию, не обращающуюся в нуль в точке
[0, 1]. Возьмем в качестве y(t) какую-нибудь функцию, не обращающуюся в нуль в точке ![]() 0
, y(
0
, y(![]() 0
) = a
0
) = a ![]() 0. Для такой функции равенство (t -
0. Для такой функции равенство (t - ![]() 0
)x(t) = y(t), не может тождественно удовлетворяться ни при какой непрерывной на отрезке [0, 1] функции x(t), ибо в точке t =
0
)x(t) = y(t), не может тождественно удовлетворяться ни при какой непрерывной на отрезке [0, 1] функции x(t), ибо в точке t = ![]() 0
левая часть его равна нулю, в то время как правая отлична от нуля. Следовательно, при
0
левая часть его равна нулю, в то время как правая отлична от нуля. Следовательно, при ![]() =
= ![]() 0
уравнение Аx=
0
уравнение Аx=![]() x не имеет решения для произвольной правой части, что и доказывает принадлежность
x не имеет решения для произвольной правой части, что и доказывает принадлежность ![]() 0
спектру оператора A. Вместе с тем ни одна точка спектра не является собственным значением, так как решение однородного уравнения (t -
0
спектру оператора A. Вместе с тем ни одна точка спектра не является собственным значением, так как решение однородного уравнения (t - ![]() )x(t) = 0,
)x(t) = 0, ![]()
![]() [0, 1], при любом t, отличном от
[0, 1], при любом t, отличном от ![]() , а следовательно, в силу непрерывности и при t =
, а следовательно, в силу непрерывности и при t = ![]() , обращается в нуль, т.е. тождественно равно нулю.
, обращается в нуль, т.е. тождественно равно нулю.
2) Пусть оператор А действующий из Е ![]() Е, задается матрицей А=
Е, задается матрицей А=![]() .
.
Аx = ![]()
![]() =
= 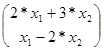 .
.
Введем обозначения:
![]() = y1
= y1
![]() = y2
= y2
x1
, x2
, y1
, y2
![]() E;
E;
A - ![]() *I =
*I = ![]() , найдем определитель A -
, найдем определитель A - ![]() *I:
*I:
D(A - ![]() *I) =
*I) = 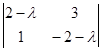 = (2-
= (2-![]() )*(-2-
)*(-2-![]() ) – 3 =
) – 3 = ![]() 2
– 7;
2
– 7;
Если определитель отличен от нуля, то есть если ![]() не есть корень уравнения
не есть корень уравнения ![]() 2
– 7 = 0, следовательно, все такие значения параметра
2
– 7 = 0, следовательно, все такие значения параметра ![]() регулярные.
регулярные.
Корни уравнения ![]() 2
– 7 = 0 образуют спектр:
2
– 7 = 0 образуют спектр:
![]() 1
=
1
= ![]() ;
; ![]() 2
= -
2
= -![]() ;
;
![]() 1
,
1
, ![]() 2
– собственные значения.
2
– собственные значения.
Найдем собственные векторы для собственных значений ![]() :
:
при ![]() =
= ![]() получаем:
получаем:
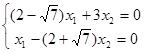
откуда x1
= (2+![]() )x2
; 1-й собственный вектор: ((2+
)x2
; 1-й собственный вектор: ((2+![]() )x, x);
)x, x);
при ![]() = -
= -![]() получаем:
получаем:
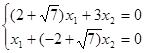
откуда x1
= (2 - ![]() )x2
; 2-й собственный вектор: ((2 -
)x2
; 2-й собственный вектор: ((2 - ![]() )x, x);
)x, x);
§4. Оператор умножения на непрерывную функцию
Рассмотрим пространство ![]() непрерывных на отрезке
непрерывных на отрезке ![]() функций, и оператор А, заданный формулой:
функций, и оператор А, заданный формулой:
Ах(t) = g(t) x(t).
g(t) - функция, непрерывная на [a, b]; a,b![]() R.
R.
Проверим является ли оператора А линейным, то есть, по определению 1, должны выполняться аксиомы аддитивности и однородности.
1) Аксиома аддитивности: A(f+g) = A(f) + A(g).
A(f+g) = (g(t)+f(t))x(t) = g(t)x(t)+f(t)x(t) = A(f) + A(g).
2) Аксиома однородности: A(k*f) = k*A(f).
A(k*f) = A(k*x(t)) = k*g(t)x(t) = kA(x(t)) = k*A(f).
По средствам арифметических операции над функциями, аксиомы аддитивность и однородность выполняются. Оператор А является линейным по определению.
3) Проверим, является ли А непрерывным, для этого воспользуемся определением непрерывности:
p (fn
(x), f0
(x)) ![]() 0
0 ![]() p (A fn
(x), Af0
(x))
p (A fn
(x), Af0
(x)) ![]() 0.
0.
Оператор А, действует в пространстве C[
![]() ]
, в котором расстояние между функциями определяется следующим образом:
]
, в котором расстояние между функциями определяется следующим образом:
p (fn
(x), f0
(x)) = ![]() | fn
(x) - f0
(x)|.
| fn
(x) - f0
(x)|.
Решение:
p (A xn
(t), Ax0
(t)) = ![]() |Axn
(t) - Ax0
(t)| =
|Axn
(t) - Ax0
(t)| = ![]() |xn
(t)g(t) - x0
(t)g(t)|
|xn
(t)g(t) - x0
(t)g(t)| ![]()
![]() |g(t)|
|g(t)| ![]() |xn
(t) - x0
(t)| =
|xn
(t) - x0
(t)| = ![]() |g(t)|p (xn
(t), x0
(t))
|g(t)|p (xn
(t), x0
(t)) ![]() 0.
0.
Итак, p (A xn
(t), Ax0
(t)) ![]() 0. Следовательно по определению 2 оператор А является непрерывным, а по теореме 3 он ограничен.
0. Следовательно по определению 2 оператор А является непрерывным, а по теореме 3 он ограничен.
4) Оператор А ограниченный, следовательно у него можно найти норму.
По определению 5: ||A||=![]() |A(f)|.
|A(f)|.
Решение.
||A||=![]() |A(f)|=
|A(f)|=![]() |g(t)x(t)|.
|g(t)x(t)|.
|g(t)x(t)| ![]() |g(t)
|g(t) ![]() x(t)| = |g(t)| |
x(t)| = |g(t)| |![]() x(t)|
x(t)| ![]()
![]() |x(t)| |g(t)|.
|x(t)| |g(t)|.
||A||=![]()
![]() |x(t)| |g(t)| =
|x(t)| |g(t)| = ![]() ||x(t)|| |g(t)|
||x(t)|| |g(t)| ![]() |g(t)|.
|g(t)|.
Норма оператора А: ||A|| = |g(t)|.
5) Обратимость оператора А, его спектр и резольвента.
Возьмем произвольное число ![]() и составим оператор
и составим оператор ![]() :
:
(А- l I ) x (t) = (g(t) –l ) х(t).
Чтобы найти обратный оператор, нужно решить уравнение ![]() относительно функции
относительно функции ![]() . Это возможно, если
. Это возможно, если ![]() для любого
для любого ![]() :
:
![]() .
.
Если число ![]() не является значение функции g(t), то знаменатель не обращается в 0, и функция
не является значение функции g(t), то знаменатель не обращается в 0, и функция ![]() непрерывна на данном отрезке, а, значит, ограничена: существует такое число С, что на всем отрезке
непрерывна на данном отрезке, а, значит, ограничена: существует такое число С, что на всем отрезке ![]() . Отсюда следует, что оператор
. Отсюда следует, что оператор ![]() является ограниченным.
является ограниченным.
Если же ![]() , то оператор
, то оператор ![]() не существует. Следовательно, спектр оператора состоит из всех l = g(t).
не существует. Следовательно, спектр оператора состоит из всех l = g(t).
Резольвента оператора имеет вид ![]() .
.
Отметим, что точки спектра ![]() ,
, ![]() , не являются собственными числами. Не существует такой непрерывной функции
, не являются собственными числами. Не существует такой непрерывной функции ![]() , для которой
, для которой ![]() , или
, или ![]() . Поэтому весь спектр данного оператора является непрерывным.
. Поэтому весь спектр данного оператора является непрерывным.
Вывод:
Оператор A, заданный формулой: Ах(t) = g(t)x(t), где g(t) - функция, непрерывная на [a, b], a,b![]() R:
R:
1. линейный;
2. непрерывный;
3. ограниченный, с нормой ||A|| = |g(t)|;
4. обратим при ![]() , для любого
, для любого ![]() ;
;
5. спектр оператора состоит из всех l = g(t); спектр данного оператора является непрерывным;
6. резольвента имеет вид ![]() .
.
§5. Оператор интегрирования
Рассмотрим оператор интегрирования, действующий в пространстве непрерывных функций - C[ a , b ] , определенных на отрезке [a,b], заданный следующим образом:
Аf(t) = 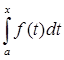 .
.
f(t) – функция, непрерывная на [a, b],t ![]() [a,x]; x
[a,x]; x ![]() [a,b]; a,b
[a,b]; a,b![]() R;
R;
Поскольку 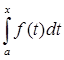 - интеграл с переменным верхним пределом, есть функция от верхнего предела – F(x), a
- интеграл с переменным верхним пределом, есть функция от верхнего предела – F(x), a ![]() x
x ![]() b; Следовательно можно утверждать, что А – оператор.
b; Следовательно можно утверждать, что А – оператор.
Проверим оператор A на линейность. По определению 1:
1) Аксиома аддитивности: A(f+g) = A(f) + A(g).
A(f+g) = 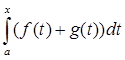 =
= 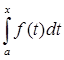 +
+ 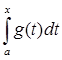 = A(f) + A(g).
= A(f) + A(g).
2) Аксиома однородности: A(kf) = kA(f).
A(kf) = 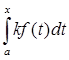 = k*
= k*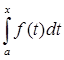 = kA(f).
= kA(f).
Исходя из свойств интеграла:
1. интеграл от суммы, есть сумма интегралов;
2. вынесение const за знак интеграла.
Можно сделать вывод: оператор А является линейным.
3) Проверим, является ли А непрерывным, для этого воспользуемся определением непрерывности:
p (fn
(t), f0
(t)) ![]() 0
0 ![]() p (A fn
(t), Af0
(t))
p (A fn
(t), Af0
(t)) ![]() 0.
0.
Оператор А, действует в пространстве C[ a , b ] , в котором расстояние между функциями определяется следующим образом:
p (fn
(t), f0
(t)) = ![]() | fn
(t) - f0
(t)|.
| fn
(t) - f0
(t)|.
Решение:
p (A fn
(t), Af0
(t)) = ![]() |
| -
- 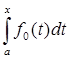 |.
|.
| -
- 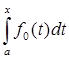 | = |
| = |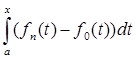 |
| ![]()
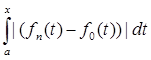
![]()
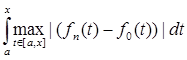 = p (fn
(t), f0
(t))
= p (fn
(t), f0
(t)) ![]() = p (fn
(t), f0
(t)) (x-a)
= p (fn
(t), f0
(t)) (x-a) ![]() 0
0
a![]() x
x![]() b.
b.
Таким образом p (A fn
(t), Af0
(t)) ![]() 0. следовательно по определению 2 оператор А непрерывен.
0. следовательно по определению 2 оператор А непрерывен.
4) Непрерывный оператор является ограниченным (теорема 3):
|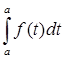 |
| ![]() |
|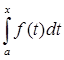 |
| ![]() |
|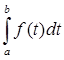 |
|
|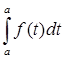 | = 0; |
| = 0; |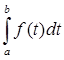 | = |b-a|.
| = |b-a|.
0 ![]() |
|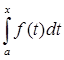 |
| ![]() |b-a|.
|b-a|.
5) Оператор А ограниченный, следовательно у него можно найти норму. Найдем норму оператора А (используя определение ||A||=![]() |A(f)|):
|A(f)|):
||A|| = ![]() |A(f)| =
|A(f)| = ![]() |
|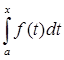 |
| ![]()
![]()
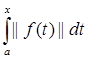
![]()
![]()
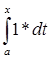 = (x-a);
= (x-a);
a ![]() x
x ![]() b;
b;
Норма оператора А: ||A|| = (b-a);
6) Обратимость интегрального оператора и его спектр.
Возьмем пространство S = {f ![]() C[0,
b
]
/ f(0) = 0} с нормой ||f|| =
C[0,
b
]
/ f(0) = 0} с нормой ||f|| = ![]() |f(x)|.
|f(x)|.
В пространстве S рассмотрим оператор А:
Аf = 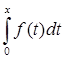
x ![]() [0,b], t
[0,b], t ![]() [0,x];
[0,x];
Найдем оператор обратный к (A - ![]() *I),
*I), ![]()
![]() R;
R;
(A - ![]() *I)*f = g
*I)*f = g
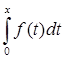 -
- ![]() *f(x) = g(x) (1)
*f(x) = g(x) (1)
Пусть функции f и g дифференцируемы;
Продифференцируем уравнение (1), получим:
f - ![]() *f/
= g/
(2)
*f/
= g/
(2)
Это уравнение (2) – дифференциальное неоднородное линейное уравнение. Решим это уравнение, используя метод Бернулли.
![]() - f/
=
- f/
= ![]()
![]() -
- ![]() + f/
= 0 (3)
+ f/
= 0 (3)
Представим решение уравнения в виде: f(x) = U(x)*V(x), тогда уравнение (3) примет вид:
![]() -
- ![]() *U*V + U/
*V + U*V/
= 0
*U*V + U/
*V + U*V/
= 0
U/
*V + U*V/
- ![]() *U*V = -
*U*V = - ![]()
U/
*V + U*(V/
- ![]() *V) = -
*V) = - ![]() (4)
(4)
Решаем однородное линейное уравнение:
V/
- ![]() *V = 0
*V = 0
V/
= ![]() *V
*V
![]() =
= ![]() *V
*V
![]() =
= ![]()
LnV = ![]() + c
+ c
V = ![]() *
*![]() , пусть
, пусть ![]() = с1
= с1
V = с1
*![]()
Подставим частное решение однородного уравнения в уравнение (4) при условии, что V/
- ![]() *V = 0.
*V = 0.
Получим уравнение:
U/
* с1
*![]() = -
= - ![]()
![]() = -
= -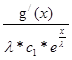
![]() = -
= - ![]() *
*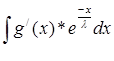
U = -![]() *
*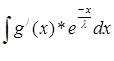
Подставим U и V в f(x) = U(x)*V(x) и получим:
f(x) = с1
*![]() *(-
*(-![]() )*
)*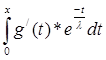
найдем интеграл Y = 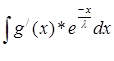 , интегрируем по частям:
, интегрируем по частям:
dz = g/ (x)dx;
z = 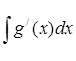 = g(x);
= g(x);
j = ![]() ;
;
dj = - ![]() *
*![]() dx;
dx;
Y = g(x)* ![]() +
+ ![]() *
*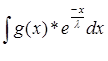
Подставим полученное значение в выражение f(x), которое примет вид:
f(x) = -![]() -
- ![]() *
*![]() *
*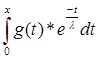 ;
;
Получим оператор В:
Bg = -![]() -
- ![]() *
*![]() *
*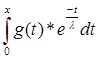 ;
;
x ![]() [0,b], t
[0,b], t ![]() [0,x], g(x)
[0,x], g(x) ![]() S,
S, ![]() - произвольное число.
- произвольное число.
Оператор В не существует, если ![]() = 0;
= 0;
Рассмотрим ограниченность оператора В для всех ![]()
![]() R,
R, ![]()
![]() 0;
0;
||Bg|| = ||f(x)|| = ![]() |f(x)| =
|f(x)| = ![]() |-
|-![]() -
- ![]() *
*![]() *
*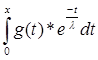 |
| ![]()
![]() (|
(|![]() | + |
| + |![]() *
*![]() *
*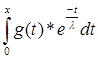 |)
|) ![]()
![]() |
|![]() | +
| + ![]() |
|![]() *
*![]() *
*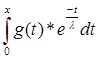 |
| ![]()
![]() |
|![]() | +
| + ![]() |
|![]() *
*![]() |*
|*![]() |g(x)*
|g(x)* ![]() |*|x|
|*|x| ![]()
![]() *
*![]() |g(x)| +
|g(x)| + ![]()
![]()
![]() *
*![]() |g(x)|*
|g(x)|* ![]() (|
(|![]() |*|x|)
|*|x|) ![]()
![]() |g(x)|*(
|g(x)|*( ![]() +
+ ![]() *
*![]()
![]() *
*![]()
![]() *b);
*b);
При ![]() 0
0
![]()
![]() =
= ![]() ;
;
![]()
![]() = 1;
= 1;
При ![]() 0
0
![]()
![]() =1;
=1;
![]()
![]() =
= ![]() ;
;
Эти оба случая можно записать в общем виде: ![]() {1,
{1, ![]() }, тогда
}, тогда
![]() |g(x)|*(
|g(x)|*( ![]() +
+ ![]() *
*![]()
![]() *
*![]()
![]() *b)
*b) ![]()
![]() |g(x)|*(
|g(x)|*( ![]() +
+ ![]() *
*![]() {1,
{1, ![]() }*b) = ||g(x)||*(
}*b) = ||g(x)||*( ![]() +
+ ![]() *
*![]() {1,
{1, ![]() }*b);
}*b);
Итак:
||Bg|| ![]() ||g(x)||*(
||g(x)||*( ![]() +
+ ![]() *
*![]() {1,
{1, ![]() }*b);
}*b);
То есть В – ограничен.
Осталось проверить, что В – оператор, обратный к (A - ![]() *I).
*I).
Если это так, то произведение этих операторов равно единичному оператору или же (A - ![]() *I)*(Bg) = g(x).
*I)*(Bg) = g(x).
Итак, нужно доказать, что
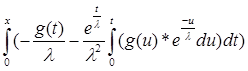 + g(x) +
+ g(x) + ![]() *
*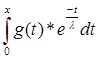 = g(x)
= g(x)
или
-![]() *
*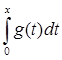 -
- ![]()
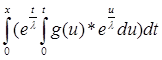 +
+ ![]() *
*![]() *
*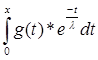 = 0; (*)
= 0; (*)
Возьмем производную от левой части (*) и получим:
-![]() *g(x) -
*g(x) - ![]() *
*![]() *
*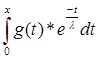 +
+ ![]() *
*![]() *
*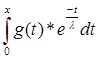 +
+ ![]() *
*![]() *
*![]() * g(x) = -
* g(x) = -![]() *g(x) +
*g(x) + ![]() *g(x) -
*g(x) - ![]() *
*![]() *
*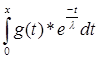 +
+ ![]() *
*![]() *
*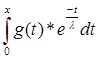 = 0;
= 0;
Следовательно, выражение (*) = const. Но, так как при x=0 выражение (*) (точнее его левая часть) равно 0, то и const=0. Значит В – обратный оператор к (A - ![]() *I) в S.
*I) в S.
Итак, мы получили ограниченный оператор В, обратный к (A - ![]() *I), который существует при
*I), который существует при ![]()
![]()
![]() R, за исключением
R, за исключением ![]() =0, то есть все возможные
=0, то есть все возможные ![]()
![]() 0 – это регулярные точки оператора А; Сам же оператор В – резольвента оператора А. Спектр оператора А – значение
0 – это регулярные точки оператора А; Сам же оператор В – резольвента оператора А. Спектр оператора А – значение ![]() при которых В не существует, то есть
при которых В не существует, то есть ![]() =0.
=0.
Вывод:
Оператор интегрирования, действующий в пространстве непрерывных функций – C[
a
,
b
]
, определенных на отрезке [a,b], заданный следующим образом: Аf(t) = 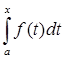 , где f(t) – функция, непрерывная на [a, b], t
, где f(t) – функция, непрерывная на [a, b], t ![]() [a,x]; x
[a,x]; x ![]() [a,b]; a,b
[a,b]; a,b![]() R:
R:
1. линейный;
2. непрерывный;
3. ограниченный: 0 ![]() |
|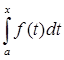 |
| ![]() |b-a|;
|b-a|;
4. норма A: ||A|| = (b-a);
5. резольвента оператора А: R![]() (A) = -
(A) = -![]() -
- ![]() *
*![]() *
*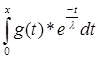 , где
, где
x ![]() [0,b], t
[0,b], t ![]() [0,x], g(x)
[0,x], g(x) ![]() S, S = {f
S, S = {f ![]() C[0,
b
]
/ f(0) = 0} с нормой ||f||=
C[0,
b
]
/ f(0) = 0} с нормой ||f||=![]() |f(x)|, g(x) =
|f(x)|, g(x) = 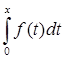 -
- ![]() *f(x),
*f(x), ![]() - произвольное число.
- произвольное число.
6. Спектр оператора А: ![]() =0.
=0.
§6. Оператор дифференцирования.
Рассмотрим оператор дифференцирования Д действующий в пространстве дифференцируемых функций – D[ a , b ] , заданный следующим образом:
Дf(x) = f/ (x);
Функция f(x) ![]() D[a, b]
, f/
(x)
D[a, b]
, f/
(x) ![]() C[a, b]
;
C[a, b]
;
Проверим оператор Д на линейность, по определению 1:
1) Аксиома аддитивности: Д(f+g) = Д(f) + Д(g).
Д(f+g) = (f+g)/ = f/ + g/ = Д(f) + Д(g).
2) Аксиома однородности: Д(kf) = kД(f).
Д(kf) = (kf) / = k(f)/ = kД(f).
Исходя из свойств производной:
1. производная от алгебраической суммы нескольких функций равна алгебраической сумме их производных;
2. постоянный множитель можно вынести за знак производной.
Можно утверждать, что Д – линейный оператор.
3) Для линейных операторов ограниченность и непрерывность оператора эквивалентны, это следует из теоремы 3.
3.1) Для начала покажем, что Д не является непрерывным оператором.
Задан оператор Дf(x) = f/
(x) подпространства E ![]() C[0, 2
C[0, 2![]() ]
, состоящего из непрерывно дифференцируемых функций, в пространство C[0, 2
]
, состоящего из непрерывно дифференцируемых функций, в пространство C[0, 2![]() ]
.
]
.
Рассмотрим f0
(x) = 0 ![]() C[0, 2
C[0, 2![]() ]
и последовательность функций fn
(x)=
]
и последовательность функций fn
(x)=![]() .
.
В пространстве E ![]() C[0, 2
C[0, 2![]() ]
: p (f0
, fn
) =
]
: p (f0
, fn
) = ![]() |
|![]() | =
| = ![]()
![]() 0, следовательно fn
0, следовательно fn
![]() f0
.
f0
.
Рассмотрим последовательность образов: Д(fn ) = cos(nx).
Имеем:
p (Дfn
, Дf0
) = ![]() |cos(nx)|
|cos(nx)| ![]()
![]() = 1.
= 1.
Это означает, что Дfn не может сходиться к Дf0 , то есть отображение Д терпит разрыв в f0 .
Поскольку оператор не является непрерывным, то, следовательно, он и не является ограниченным.
3.2) Теперь покажем, как из неограниченности оператора следует его разрывность.
Пусть оператор Д действует из C[0, 1] в C[0, 1] , оператор Дf(x) = f/ (x);
Этот оператор определен не на всем пространстве непрерывных функций, а лишь на подпространстве непрерывных функций, имеющих непрерывную производную.
В пространстве C[0, 1]
норма ||f|| = ![]() |f(t)|.
|f(t)|.
Возьмем из C[0, 1]
последовательность fn
(t) = tn
. Она ограничена в C[0, 1]
: ||fn
(t)|| = ![]() |tn
| = 1.
|tn
| = 1.
Рассмотрим Д fn (t): Д fn (t) = f/ n (t) = n tn-1 ;
||f/
n
(t)|| = ![]() |n tn-1
| = n.
|n tn-1
| = n.
В результате получили, что оператор Д переводит ограниченное множество в неограниченное, значит, по определению этот оператор не является ограниченным, а по теореме 3 не является непрерывным.
Вывод:
Оператор дифференцирования Д действующий в пространстве дифференцируемых функций – D[
a
,
b
]
, заданный следующим образом: Дf(x)=f/
(x), где функция f(x) ![]() D[
a
,
b
]
, f/
(x)
D[
a
,
b
]
, f/
(x) ![]() C[
a
,
b
]
:
C[
a
,
b
]
:
1. линейный;
2. не ограниченный;
3. не непрерывный.
§7. Оператор сдвига
Рассмотрим оператор А, действующий в пространстве непрерывных и ограниченных функций – C[
![]() ]
, заданный следующим образом:
]
, заданный следующим образом:
Af(x) = f(x+a).
Функции f(x), f(x+a) ![]() C[
C[
![]() ]
, a
]
, a ![]() R, f(x+a) – непрерывная и ограниченная функция.
R, f(x+a) – непрерывная и ограниченная функция.
Покажем линейность оператора А, по определению 1 должны выполняться следующие аксиомы :
1) Аксиома аддитивности: А(f+g) = А(f) + А(g).
А(f+g) = (f+g)(x+a) = f(x+a) + g(x+a) = А(f) + А(g).
По определению суммы функции, аксиома верна.
2) Аксиома однородности: А(kf) = kА(f).
A(k*f(x)) = k*f(x+a) = k*A(f(x)).
Аксиомы 1 и 2 верны, следовательно можно сделать вывод, что А – линейный оператор.
3) Проверим является ли оператор A непрерывным, для этого воспользуемся определением непрерывности:
p (fn
(x), f0
(x)) ![]() 0
0 ![]() p (A fn
(x), Af0
(x))
p (A fn
(x), Af0
(x)) ![]() 0.
0.
Оператор А действует в пространстве C[
![]() ]
, в котором расстояние между функциями определяется следующим образом:
]
, в котором расстояние между функциями определяется следующим образом:
p (fn
(x), f0
(x)) = ![]() | fn
(x) - f0
(x)|.
| fn
(x) - f0
(x)|.
Решение:
p (A fn
(x), Af0
(x)) = ![]() |Afn
(x) - Af0
(x)| =
|Afn
(x) - Af0
(x)| = ![]() |fn
(x+a) - f0
(x+a)| =
|fn
(x+a) - f0
(x+a)| = 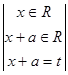 =
= ![]() |fn
(t) - f0
(t)| = p (fn
(t), f0
(t))
|fn
(t) - f0
(t)| = p (fn
(t), f0
(t)) ![]() 0.
0.
Таким образом p (A fn
(x), Af0
(x)) ![]() 0. Следовательно оператор А непрерывен.
0. Следовательно оператор А непрерывен.
4) Непрерывный оператор является ограниченным, а у ограниченного оператора есть норма, найдем норму оператора А (по определению 5):
||A|| = ![]() |Af| =
|Af| = ![]() |f(x+a)|
|f(x+a)| ![]() 1.
1.
Поскольку ||f|| = ![]() |f(x)|
|f(x)| ![]() 1.
1.
Норма А: ||A|| = 1.
5) Обратимость оператора А: Af(x) = f(x+a)
Такой оператор A сдвигает функцию на const a; обратный к A оператор будет сдвигать функцию на const (-a):
A-1 f(x) = f(x-a).
6) Спектр оператора А.
Рассмотрим пространство непрерывных функций – С[0, +![]() )
, имеющих конечный предел на
)
, имеющих конечный предел на ![]() :
:
Af(x) = f(x+a), a![]() 0.
0.
Вопрос о спектре оператора А касается разрешимости в пространствах С[0,
b
)
и С[а,+![]() )
.
)
.
Введем функцию V(x) = ![]() при |
при |![]() |1,
|1, ![]()
![]() 0, найдем ее предел:
0, найдем ее предел:
![]()
![]() = 0
= 0
Следовательно рассмотренная функция входит в пространство С[0,+![]() )
.
)
.
Теперь рассмотрим V(x+a) = ![]() =
= ![]() *
*![]() =
= ![]() *V(x).
*V(x).
Для ![]() =0 подберем непрерывную функцию = 0 при x
=0 подберем непрерывную функцию = 0 при x ![]() а и не равную 0 при x
а и не равную 0 при x ![]() [0, a]. Для этой функции A(V(x)) = 0 то есть она является собственным вектором для числа 0; функция V(x) = с, так же удовлетворяет разностному отношению
[0, a]. Для этой функции A(V(x)) = 0 то есть она является собственным вектором для числа 0; функция V(x) = с, так же удовлетворяет разностному отношению ![]() V(x) - V(x+a) = 0. Значит
V(x) - V(x+a) = 0. Значит ![]() =1
=1 ![]() точечному спектру и в том и в другом пространстве. И все точки внутри единичного круга
точечному спектру и в том и в другом пространстве. И все точки внутри единичного круга ![]() точечному спектру.
точечному спектру.
Покажем, что остальные точки окружности ![]() точечному спектру оператора А в пространстве С[0, +
точечному спектру оператора А в пространстве С[0, +![]() )
.
)
.
Рассмотрим U(x) = ![]() и число
и число ![]() =
= ![]() (|
(|![]() | = 1);
| = 1);
U(x+a) = 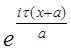 =
= ![]()
![]() =
= ![]() U(x);
U(x);
U(x) = ![]() = Cos(
= Cos(![]() ) + iSin(
) + iSin(![]() ), принадлежит пространству С[0,
b
)
так как мнимая и действительная части – функции ограниченные, но не принадлежат пространству С[
a
, +
), принадлежит пространству С[0,
b
)
так как мнимая и действительная части – функции ограниченные, но не принадлежат пространству С[
a
, +![]() )
так как не имеют конечного предела на
)
так как не имеют конечного предела на ![]() .
.
Если точки лежат вне единичного круга, то они регулярные для оператора А в 2-х пространствах.
Покажем, что в пространстве С[0, +![]() )
точки
)
точки ![]() =
= ![]() ,
, ![]()
![]() 2
2![]() n не будут собственными числами.
n не будут собственными числами.
Докажем это от противного: пусть найдется ![]() =
= ![]() ,
, ![]()
![]() 2
2![]() n – собственное число, тогда найдется функция f(x)
n – собственное число, тогда найдется функция f(x) ![]() С[0, +
С[0, +![]() )
, что
)
, что
f(x+a) = ![]() f(x).
f(x).
Применим оператор А n раз: f(x+n*a) = ![]() n
f(x), тогда
n
f(x), тогда
![]() f(x+na) =
f(x+na) = ![]()
![]() n
f(x), у левой части предел конечен;
n
f(x), у левой части предел конечен;
правая часть предела не имеет, так как не имеет предела последовательность ![]() n
=
n
= ![]() = Cos(
= Cos(![]() n) + iSin(
n) + iSin(![]() n).
n).
Следовательно ![]() =
= ![]() ,
, ![]()
![]() 2
2![]() n собственным числом не является.
n собственным числом не является.
Эти точки будут принадлежать спектру оператора А в пространстве С[0,+![]() )
, так как спектр замкнутое множество и граница единичного круга должна принадлежать спектру оператора А в пространстве С[0, +
)
, так как спектр замкнутое множество и граница единичного круга должна принадлежать спектру оператора А в пространстве С[0, +![]() )
.
)
.
Сделаем вывод:
При |![]() |1 все точки регулярные
;
|1 все точки регулярные
;
При |![]() |1 и
|1 и ![]() =1 – точки спектра;
=1 – точки спектра;
При ![]() =
= ![]() ,
, ![]()
![]() 2
2![]() n – точки непрерывного спектра.
n – точки непрерывного спектра.
Вывод:
Оператор А, действующий в пространстве непрерывных и ограниченных функций – C[
![]() ]
, заданный следующим образом: Af(x) = f(x+a), где функции f(x), f(x+a)
]
, заданный следующим образом: Af(x) = f(x+a), где функции f(x), f(x+a) ![]() C[
C[
![]() ]
, a
]
, a ![]() R, f(x+a) – непрерывная и ограниченная функция:
R, f(x+a) – непрерывная и ограниченная функция:
1. линейный;
2. непрерывный и ограниченный;
3. норма А: ||A|| = 1;
4. A-1 f(x) = f(x-a);
5. Спектр оператора А:
· при |![]() |1 и
|1 и ![]() =1 – точки спектра;
=1 – точки спектра;
· при ![]() =
= ![]() ,
, ![]()
![]() 2
2![]() n – точки непрерывного спектра;
n – точки непрерывного спектра;
· При |![]() |1 все точки регулярные.
|1 все точки регулярные.
Заключение
В ходе проделанной работы были рассмотрены основные определения теории линейных операторов: непрерывность, ограниченность, норма, спектр оператора и резольвента. Проведено исследование четыре оператора: оператор умножения на непрерывную функцию, оператор интегрирования, оператор дифференцирования, оператор сдвига. Можно сказать, что поставленные цели были достигнуты.
Список литературы
1. Колмогоров, А.Н. Элементы теории функций и функционального анализа [Текст]/ А.Н. Колмогоров, С.В. Фомин. – М.: Наука; Главная редакция физико–математической литературы, 1972.
2. Соболев, В.И. Лекции по дополнительным главам математического анализа [Текст] / В.И. Соболев. - М.: Наука, 1968.
3. Петров, В.А., Виленкин, Н.Я, Граев, М.И. Элементы функционального анализа в задачах [Текст]/ В.А. Петров, Н.Я. Виленкин, М.И. Граев под ред. О.А. Павлович. - М.: Просвещение, 1978.
4. Данфорд, Н. Линейные операторы. Общая теория [Текст]/ Н. Данфорд, Дж.Т. Шварц; под ред. А.Г. Костюченко; пер. с англ. Л.И. Головина, Б.С. Литягина. – М.: Издательство иностранной литературы, 1926.
[1]
Ex
и Ey
- линейные многообразия, то есть если x, y ![]() Ex
, то
Ex
, то ![]() x +
x + ![]() y
y ![]() Ey
, при
Ey
, при ![]()
![]() ,
, ![]() .
.
Ex – область определения А;
Ey - область значения А;
[2] Равенства 1 и 2 определяются как аксиомы аддитивности и однородности;
[3] Шаром в метрическом пространстве называется совокупность элементов x пространства, удовлетворяющих условию p ( xn , x 0 ) а.
Шар D ( x 0 , a ).
Если
p
(
xn
,
x
0
) ![]() а, то
D
(
x
0
,
a
) – замкнутый шар.
а, то
D
(
x
0
,
a
) – замкнутый шар.
Если p ( xn , x 0 ) = а, то S ( x 0 , a ) – сфера.
Всякий шар метрического пространства, содержащий точку y , называется окрестностью точки y .
[4] Свойства нормы оператора.
1) Если оператор ![]() ограничен,
ограничен, ![]() , то и оператор
, то и оператор ![]() ограничен, причем
ограничен, причем ![]() .
.
2) Если операторы ![]() ограничены, то и оператор
ограничены, то и оператор ![]() ограничен, причем
ограничен, причем ![]() и
и ![]() .
.
[5] Линейный функционал, есть частный случай линейного оператора. Именно, линейный функционал есть линейный оператор, переводящий пространство E в числовую прямую.
[6] Резольвента – это функция комплексного переменного со значениями во множестве операторов, определенная на множестве регулярных чисел данного оператора.