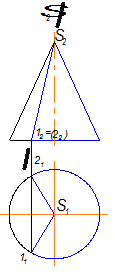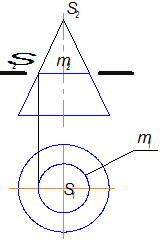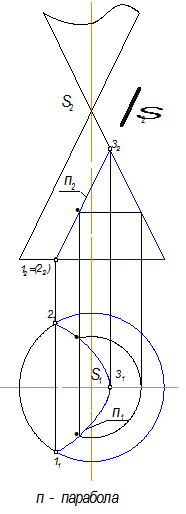Проекционное черчение, аксонометрия

СОДЕРЖАНИЕ: Содержит сведения и правила построения изображений на технических чертежах, правила оформления чертежей в соответствии с государственными стандартами, примеры решения задач по проекционному черчению, методы построения наглядных изображений деталей

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Тольяттинский государственный университет

Автомеханический институт

Кафедра Начертательная геометрия и черчение

МОДУЛЬ №5

ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ, АКСОНОМЕТРИЯ,

НАКЛОННОЕ СЕЧЕНИЕ

Учебно-методическое пособие к выполнению графических работ

г.Тольятти

2008 год

УДК 744 ( 075. 8)

ББК 30.11

М31

Модуль №5. Проекционное черчение, аксонометрия и наклонное

сечение.

Учебно-методическое пособие к выполнению графических работ

/ Сост. Буткова Т.А., Масакова Н.И., Уполовникова Г.Н.

Яковлева Т.М.-Тольятти, ТГУ, 2008-С.

Содержит сведения и правила построения изображений на технических чертежах, правила оформления чертежей в соответствии с государственными стандартами, примеры решения задач по проекционному черчению, методы построения наглядных изображений деталей.

Для студентов технических специальностей высших учебных заведений.

Рецензент: к.т.н., доцент Виткалов В.Г.

Научный редактор: к.п.н., доцент Варенцова Т.А.

Утверждено НМС Автомеханического института ТГУ

Тольяттинский государственный университет, 2008

Содержание

Изображения на технических чертежах. 5

1.Основные положения. 5

2.Виды. 6

2.1.Основные виды.. 6

2.2.Местные виды. 7

2.3. Дополнительные виды. 8

3.Разрезы. 9

3.1. Построение разрезов. 10

3.2 Обозначение разрезов. 11

3.3Штриховка материалов в разрезах и сечениях. 12

3.4. Классификация разрезов. 13

3.4.1 Простые разрезы.. 14

3.4.2. Местные разрезы.. 16

3.4.3.Соединение части вида и части разреза. 17

3.4.4. Сложные разрезы. 20

4. Сечения. 21

4.1. Построение сечений. 21

4.2. Расположение сечений. 22

4.3. Отличие разреза от сечения. 23

4.4. Обозначение сечений. 24

4.5 Некоторые правила построения сечений. 24

5.Выносные элементы. 26

6. Условности и упрощения, применяемые при выполнении изображений. 26

7.Содержание заданий. 33

8. Сведения о поверхностях. 43

Построение линий, принадлежащих поверхностям. 43

Поверхности. 43

8.1. Призма. 44

8.2. Пирамида. 44

8.3. Тела, ограниченные поверхностями вращения. 45

8.3.1. Цилиндр вращения. 46

8.3.2.Конус вращения. 49

8.3.3. Сфера. 52

9. Примеры выполнения заданий. 53

10.Аксонометрия. 60

10.1. Краткие теоретические сведения об аксонометрических проекциях. 60

10.2.1. Прямоугольная изометрия. 64

10.2.2. Изометрия окружности. 66

10.3. Этапы выполнения наглядного изображения детали. 71

10.4Прямоугольная диметрия. 76

10.4.1. Построение окружностей в прямоугольной диметрии. 78

10.5.Косоугольная диметрическая проекция (фронтальная) 78

11.Наклонные сечения. 80

Контрольные вопросы.. 85

Библиографический список. 86

Изображения на технических чертежах.

1.Основные положения.

Изображения на чертежах в зависимости от содержания разделяют на виды, разрезы, сечения в соответствии с ГОСТ 2.305-68*.

Изображения предметов на чертежах получают способом прямоугольного проецирования. За основные плоскости проекций принимают шесть граней куба (рис. 1.1), грани совмещают с плоскостью, как показано на рис. 1.2.

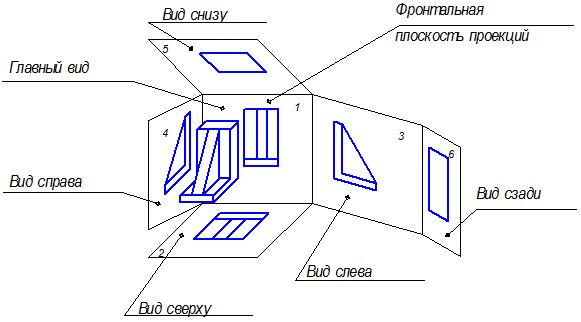
Рис.1.1

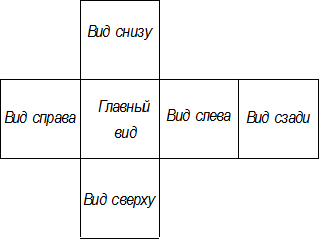
Рис.1.2

Вид-это изображение обращенной к наблюдателю видимой части поверхности предмета, полученное методом ортогонального проецирования.

Изображение на фронтальной плоскости проекций (рис. 1.1) принимается на чертеже в качестве главного вида. Предмет располагают относительно этой плоскости проекций так, чтобы изображение на ней давало наиболее полное представление о форме и размерах предмета.

2.Виды.

2.1.Основные виды

Стандарт устанавливает следующие виды, получаемые на основных плоскостях проекций (рис.1.2): вид спереди (главный), вид сверху, вид слева, вид справа, вид снизу, вид сзади.

За главный вид принимают тот, который дает наиболее полное представление о форме и размерах предмета.

Количество изображений должно быть наименьшим, но обеспечивающим полное представление о форме и размерах предмета.

Если основные виды расположены в проекционной связи, то их названия не обозначают. Для наилучшего использования поля чертежа виды допускается располагать вне проекционной связи (рис.2.2). В этом случае изображение вида сопровождается обозначением по типу:

1)указывается направление взгляда

2) над изображением вида наносят обозначение А , как на рис. 2.1.

Виды обозначаются прописными буквами русского алфавита шрифтом, на 1...2 размера превышающим шрифт размерных чисел.

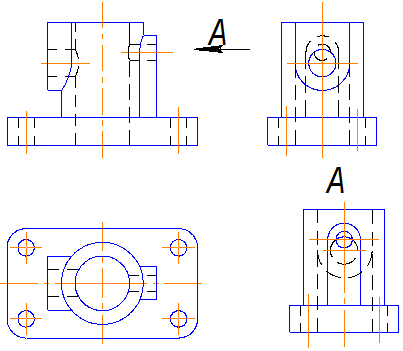
Рис. 2.1

На рисунке 2.1 показана деталь, для которой необходимо выполнить четыре вида. Если эти виды расположить в проекционной связи, то на поле чертежа они займут много места. Можно расположить необходимые виды так, как показано на рис. 2.1. Формат чертежа уменьшается, но нарушена проекционная связь, поэтому нужно выполнить обозначение вида справа ().

2.2.Местные виды.

Местным видом называется изображение отдельного ограниченного места поверхности предмета.

Он может быть ограничен линией обрыва (рис.2.3 а) или не ограничен (рис.2.3б).

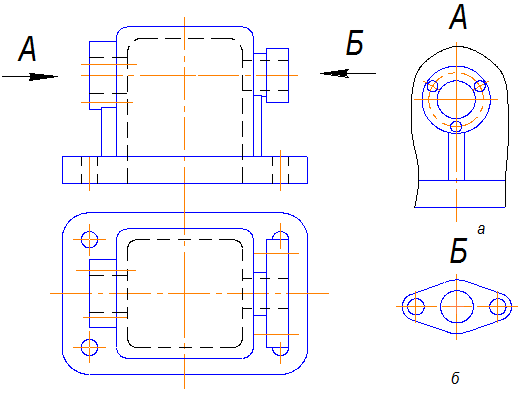
Рис. 2.3

В общем случае местные виды оформляются так же, как и основные виды.

2.3. Дополнительные виды.

Если какую-либо часть предмета невозможно показать на основных видах без искажения формы и размеров, то применяют дополнительные виды.

Дополнительным видом называется изображение видимой части поверхности предмета, получаемой на плоскости, не параллельной ни одной из основных плоскостей проекций.

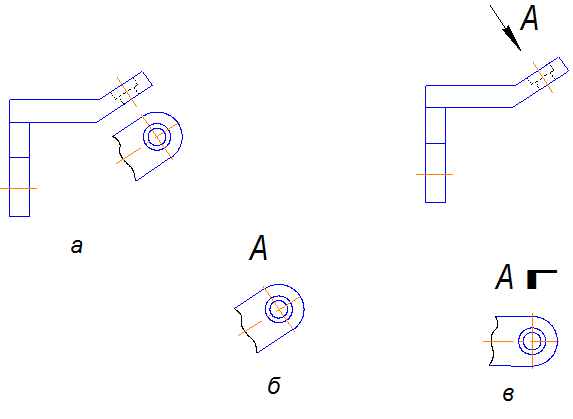
Рис. 2.4

Если дополнительный вид выполняется в проекционной связи с соответствующим изображением (рис.2.4 а), то его не обозначают.

Если изображение дополнительного вида выносится на свободное место (рис.2.4 б), т.е. нарушается проекционная связь, то направление взгляда указывается стрелкой, расположенной перпендикулярно изображаемой части детали и обозначается буквой русского алфавита, причем буква остается параллельна основной надписи чертежа, а не поворачивается за стрелкой.

При необходимости изображение дополнительного вида можно поворачивать, тогда над изображением ставится буква и знак поворота (это окружность 5...6мм со стрелкой, между створками которой угол 90°) (рис.2.4 в).

Дополнительный вид чаще всего выполняют как местный.

3.Разрезы.

Разрезом называется изображение предмета, мысленно рассеченного одной или несколькими плоскостями. На разрезе показывается то, что лежит в секущей плоскости и что расположено за ней.

При этом часть предмета, расположенную между наблюдателем и секущей плоскостью, мысленно удаляют, в результате чего все закрытые этой частью поверхности становятся видимыми.

3.1. Построение разрезов.

На рис.3.1 даны три вида предмета (без разреза). На главном виде внутренние поверхности: прямоугольный паз и цилиндрическое ступенчатое отверстие показаны штриховыми линиями.

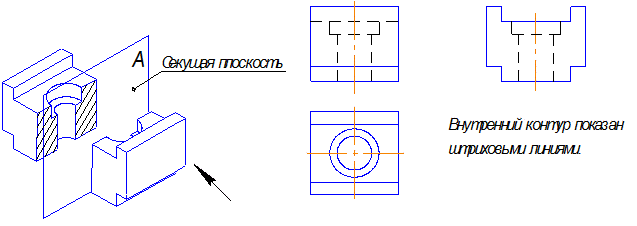
Рис. 3.1

На рис. 3.2 вычерчен разрез, полученный следующим образом.

Секущей плоскостью, параллельной фронтальной плоскости проекций, предмет мысленно рассечен вдоль своей оси, проходящей через прямоугольный паз и цилиндрическое ступенчатое отверстие, расположенное в центре предмета.. Затем мысленно была удалена передняя половина предмета , находящаяся между наблюдателем и секущей плоскостью. Так, как предмет симметричен, то нет смысла давать полный разрез. Его выполняют справа, а слева оставляют вид.

Вид и разрез разделяют штрихпунктирной линией. На разрезе показано то, что получилось в секущей плоскости и то, что находится за ней.

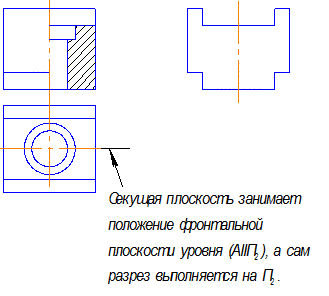
Рис. 3.2

При рассмотрении чертежа можно заметить следующее:

1) штриховые линии, которыми на главном виде обозначены прямоугольный паз и цилиндрическое ступенчатое отверстие, на разрезе обведены сплошными основными линиями, так как они стали в результате мысленного рассечения предмета видимыми;

2) на разрезе, проходившая вдоль главного вида сплошная основная линия, обозначающая срез, отпала вовсе, так как передняя половина предмета не изображается. Срез, находящийся на изображаемой половине предмета, не обозначен, так как на разрезах не рекомендуется показывать штриховыми линиями невидимые элементы предмета;

3) на разрезе штриховкой выделена плоская фигура, находящаяся в секущей плоскости, штриховка наносится только в том месте, где секущая плоскость рассекает материал предмета. По этой причине задняя поверхность цилиндрического ступенчатого отверстия не заштрихована, так же как и прямоугольный паз (при мысленном рассечении предмета секущая плоскость этих поверхностей не затронула);

4) при изображении цилиндрического ступенчатого отверстия проведена сплошная основная линия, изображающая на фронтальной плоскости проекций горизонтальную плоскость, образованную изменением диаметров;

5) разрез, помещенный на месте главного изображения, никак не изменяет изображений вида сверху и слева.

При выполнении разрезов на чертежах необходимо руководствоваться следующими правилами:

1) выполнять на чертеже только полезные разрезы (полезныминазываются разрезы, выбранные по соображениям необходимости и достаточности);

2) невидимые ранее внутренние очертания, изображаемые штриховыми линиями, обводить сплошными основными линиями;

3) фигуру сечения, входящую в разрез, штриховать;

4) мысленное рассечение предмета должно относиться только к данному разрезу и не влиять на изменение других изображений того же предмета;

5) на всех изображениях штриховые линии убираются, т. к. внутренний контур хорошо читается на разрезе.

3.2 Обозначение разрезов

Для того, чтобы знать, в каком месте предмет имеет форму, показанную на изображении разреза, место, где проходила секущая плоскость , и сам разрез обозначают. Линия, обозначающая секущую плоскость, называется линией сечения. Она изображается разомкнутой линией.

При этом выбирают начальные буквы алфавита (А, Б, В, Г, Д и т. д.). Над разрезом, полученным с помощью данной секущей плоскости, выполняют надпись по типу А-А , т.е. двумя парными буквами через тире (рис.3.3).

Буквы у линий сечения и буквы, обозначающие разрез, должны быть большего размера, чем цифры размерных чисел на том же чертеже (на один-два номера шрифта)

В случаях, когда секущая плоскость совпадает с плоскостью симметрии данного предмета и соответствующие изображения расположены на одном и том же листе в непосредственной проекционной связи и не разделены какими-либо другими изображениями, рекомендуется не отмечать положение секущей плоскости и изображение разреза не сопровождать надписью.

На рис.3.3 показан чертеж предмета, на котором выполнено два разреза.

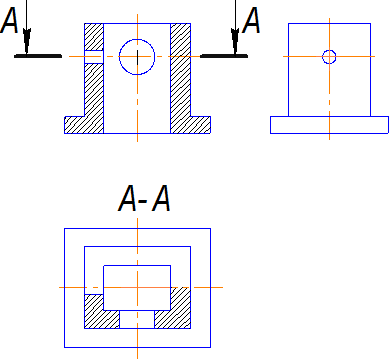
Рис.3.3

1. На главном виде разрез выполнен плоскостью, расположение которой совпадает с плоскостью симметрии для данного предмета. Она проходит вдоль горизонтальной оси на виде сверху. Поэтому этот разрез не обозначен.

2. Секущая плоскость А-А не совпадает с плоскостью симметрии данной детали, поэтому соответствующий разрез обозначен.

Буквенное обозначение секущих плоскостей и разрезов располагают параллельно основной надписи независимо от угла наклона секущей плоскости.

3.3 Штриховка материалов в разрезах и сечениях.

В разрезах и сечениях фигуру, полученную в секущей плоскости, штрихуют.

ГОСТ 2.306-68 устанавливает графическое обозначение различных материалов (рис.3.4)


Металлы и твердые сплавы	Неметаллические материалы, за исключением древесины, бетона, стекла, жидкостей, песка

Рис. 3.4

Штриховка для металлов наносится тонкими линиями под углом 45° к линиям контура изображения, или к его оси, или к линиям рамки чертежа, причем, расстояние между линиями должно быть одинаковым.

Штриховка на всех разрезах и сечениях для данного предмета одинакова по направлению и шагу (расстояние между штрихами).

3.4. Классификация разрезов.

Разрезы имеют несколько классификаций:

1. Классификация, в зависимости от количества секущих плоскостей;

2. Классификация, в зависимости от положения секущей плоскости относительно плоскостей проекций;

3. Классификация, в зависимости от положения секущих плоскостей относительно друг друга.

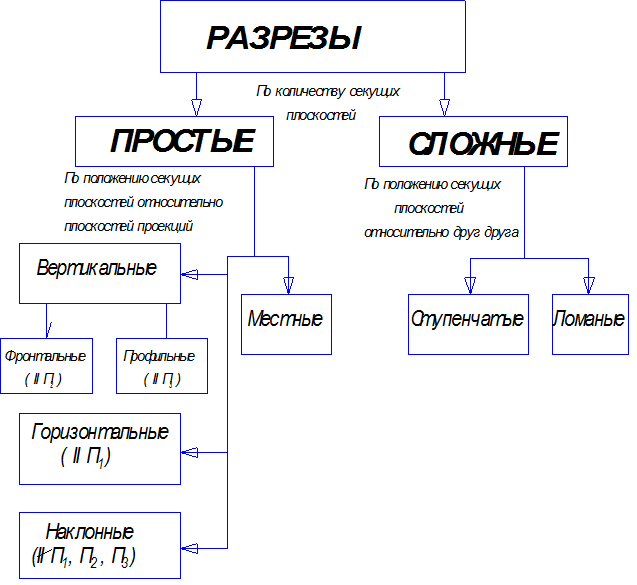Рис. 3.5

3.4.1 Простые разрезы

Простым называют разрез, выполненный одной секущей плоскостью.

Положение секущей плоскости может быть различным: вертикальным, горизонтальным, наклонным. Его выбирают в зависимости от формы предмета, внутреннее устройство которого нужно показать.

В зависимости от положения секущей плоскости относительно горизонтальной плоскости проекций разрезы подразделяются на вертикальные, горизонтальные и наклонные.

Вертикальным называется разрез при секущей плоскости, перпендикулярной горизонтальной плоскости проекций.

Вертикально расположенная секущая плоскость может быть параллельна фронтальной плоскости проекций или профильной, образуя при этом соответственно фронтальный (рис.3.6) или профильный разрезы (рис.3.7).

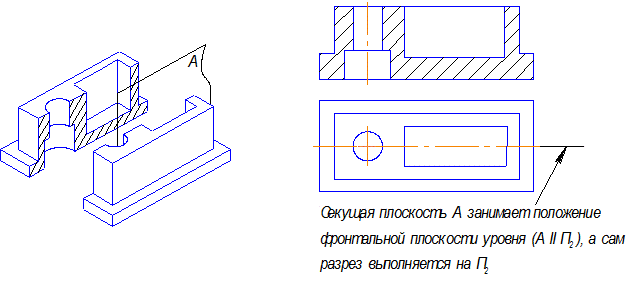
Рис. 3.6

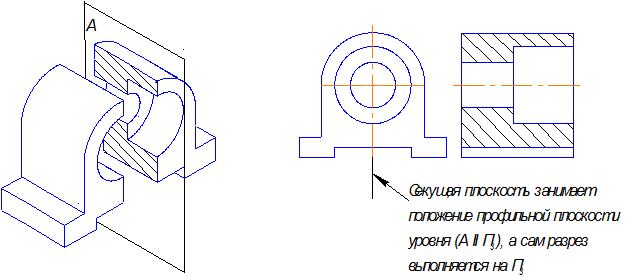
Рис. 3.7

Горизонтальным разрезом называется разрез при секущей плоскости, параллельной горизонтальной плоскости проекций (рис.3.8).

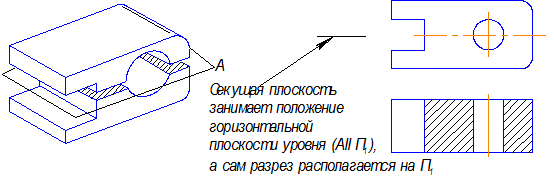
Рис. 3.8

Наклонным разрезом называется разрез при секущей плоскости, составляющей с одной из основных плоскостей проекций угол, отличный от прямого (рис.3.9).

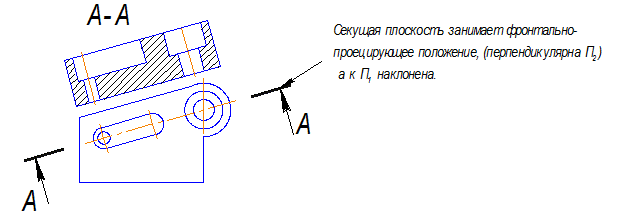
Рис. 3.9

3.4.2. Местные разрезы

Местным разрезом называется разрез, служащий для выяснения внутреннего устройства предмета лишь в отдельном ограниченном месте.

В машиностроении при вычерчивании сплошных (непустотелых) предметов полные разрезы не применяют. Однако часто в сплошных деталях имеются местные углубления или отверстия, форму которых нужно показать.

Примерами таких предметов являются валик со шпоночным пазом и ось с центровыми отверстиями (рис. 3.10).

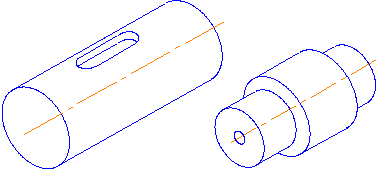
Рис. 3.10

В таких случаях применяют местный разрез. Применение полного разреза здесь нецелесообразно, так как чертеж от этого не станет яснее, а трудоемкость его выполнения возрастает. Поэтому в этом случае применим местный разрез.

Валик мысленно рассечен секущей плоскостью, проходящей через его ось, лишь в том месте, где расположен шпоночный паз (рис.3.11 а). Разрез ограничен сплошной волнистой линией.

Она не должна совпадать с какими-либо линиями изображения.

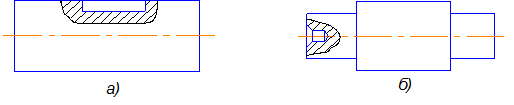
Рис. 3.11

На чертеже оси с центровым отверстием (рис.3.11 б) форма данного отверстия выявлена с помощью местного разреза на главном виде.

3.4.3.Соединение части вида и части разреза.

Форма многих предметов такова, что при их изображении недостаточно дать только разрез, так как по разрезу иногда нельзя представить внешнюю форму предмета. При изображении подобных предметов необходимо дать как разрез, т. е. выполнить два разных изображения, на что уходит много времени и места. Поэтому допускается соединять на одном изображении часть вида и часть соответствующего разреза.

При этом вид и разрез разделяют сплошной волнистой линией.

Например, на рис. 3.12 изображены два вида предмета, форма которого не будет ясна, если показать его только в разрезе. В этом случае легко будет судить о внутреннем устройстве предмета, но наружный вид станет не ясен, так как не будет оснований для определения высоты прилива на наружной ее поверхности. Поэтому выполняют местный вид с изображением цилиндрического прилива.

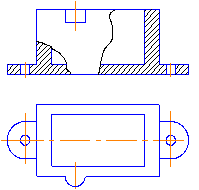
Рис. 3.12

Данный пример демонстрирует рациональный способ построения чертежа.

ГОСТ 2.305-68 рекомендует по возможности соединять половину вида и половину разреза, когда вид и разрез представляют собой симметричные фигуры. Тогда получится изображение, по которому можно судить как о наружной форме, так и о внутреннем устройстве предмета (рис.3.13).

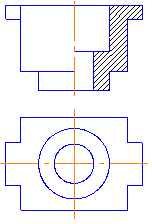
Рис. 3.13

При выполнении изображений , содержащих соединение половины вида и половины соответствующего разреза, необходимо соблюдать следующие правила:

Линией, разделяющей половину вида и половину разреза, должна служить осевая, т.е. штрихпунктирная линия.

Допускается также разделять разрез и вид штрихпунктирной линией, совпадающей со следом плоскости симметрии не всего предмета, а лишь его части, если эта часть представляет собой тело вращения. Пример такого случая представлен на рис.3.14, где изображена часть шатуна. Он имеет цилиндрический элемент (тело вращения), разрез на котором выполнен лишь до оси симметрии.

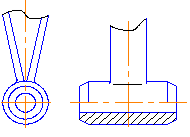
Рис.3.14

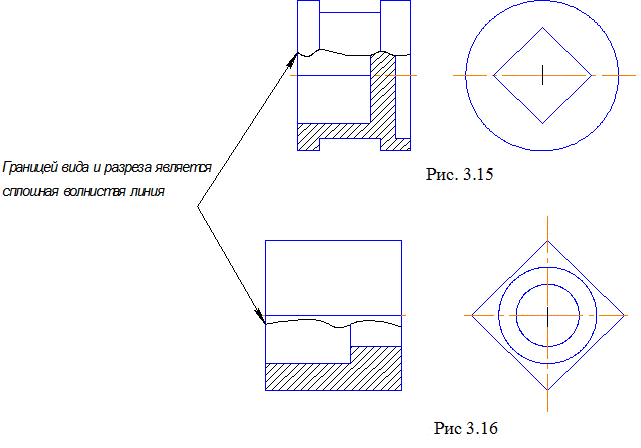
При совмещении половины вида и половины разреза в некоторых случаях с осевой совпадает линия контура (ребра многогранников). В таких случаях нужно выполнять часть вида и часть разреза, разделяя их сплошной волнистой линией. Эта линия должна быть расположена так, чтобы ребро было показано на изображении. Если оно расположено на внутренней поверхности, то дают больше половины разреза (рис. 3.15), а если на наружной, то больше половины вида (рис.3.16).

При совмещении половины вида и половины разреза вид всегда располагается слева, а разрез - справа, если ось симметрии вертикальная. При совмещении по горизонтальной оси симметрии - вид располагается сверху, а разрез снизу (рис.3.17).

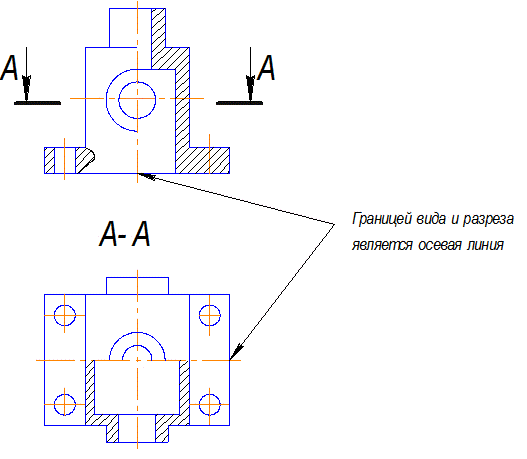
Рис. 3.17

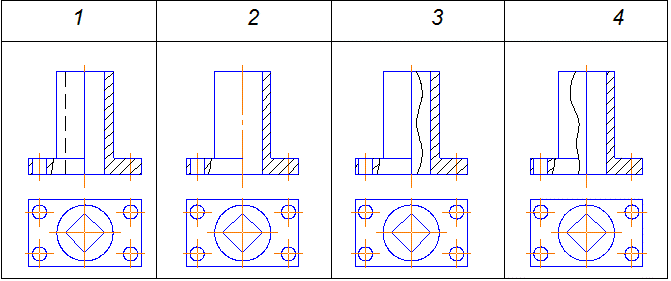
Внимание! Тест № 1.

В каком случае изображение разреза выполнено верно?

Ответ находится на странице 23.

3.4.4. Сложные разрезы.

Разрез, получаемый при помощи нескольких секущих плоскостей, называется сложным.

Сложные разрезы бывают ломаными, если секущие плоскости пересекаются (рис.3.18) и ступенчатыми, если секущие плоскости параллельны друг другу (рис.3.19)

Для выяснения устройства предмета на рис.3.18 необходимы две пересекающиеся секущие плоскости. Фигуры, лежащие в секущих плоскостях, при построении ломаных разрезов условно поворачивают вокруг линии пересечения секущих плоскостей до совмещения проекций.

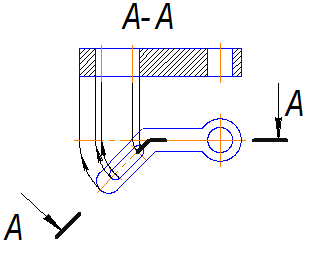
Рис. 3.18

На рис.3.19 показан сложный ступенчатый разрез. Вдоль плиты мысленно направлены три секущие плоскости, расположенные параллельно одна другой. Каждая из них выявляет форму отверстий, расположенных на разных уровнях. Таким образом, определяется внутреннее устройство предмета. Все плоские фигуры в секущих плоскостях совмещены с плоскостью чертежа, образуя сложный ступенчатый разрез.

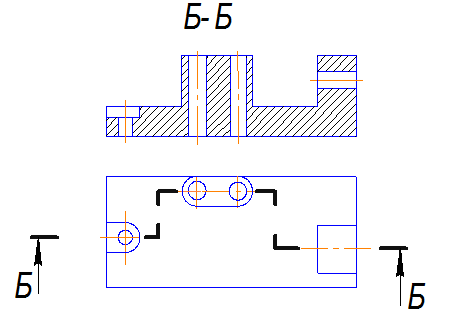
Рис. 3.19

Внимание! В обоих случаях границы плоскостей сечения на изображении разреза не показывают, изображение получается таким же, как и при рассечении одной плоскостью и сложный разрез изображают как простой.

4. Сечения

Сечением называется изображение фигуры, получающейся при мысленном рассечении предмета одной плоскостью . На сечении показывается только то, что лежит в секущей плоскости.

4.1. Построение сечений.

На рис.4.1 изображен вал, имеющий две лыски (плоские срезы с двух сторон) и шпоночный паз (прямоугольное углубление с полукруглыми концами, предназначенное для шпонки).

Чтобы сделать чертеж более ясным, строят сечения. Для этого мысленно рассекают вал двумя секущими плоскостями А и Б , перпендикулярными оси вала. Плоскость А проходит поперек лыски и показывает форму детали в этом месте.

Плоскость Б , рассекающая вал поперек шпоночного паза, выявляет его глубину и ширину.

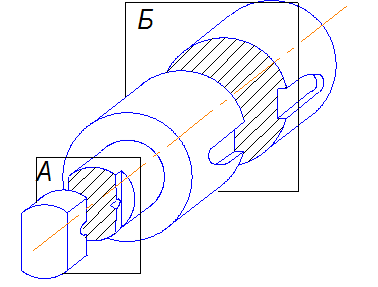
Рис. 4.1

Мысленно удалив отсеченные части вала, оставшуюся часть его рассматривают по направлению, указанному стрелками.

Изображают на чертеже только то, что находится в секущих плоскостях. Это и будут сечения. На фигуры сечения наносят штриховку (рис.4.2.)

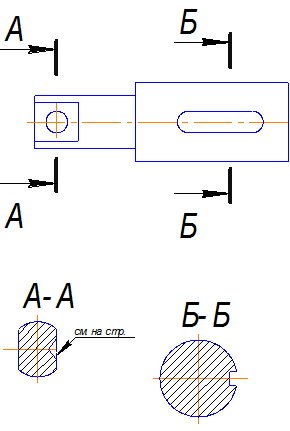
Рис.4.2

4.2. Расположение сечений.

В зависимости от расположения сечения подразделяются на вынесенные и наложенные.

Вынесенными сечениями называются такие, которые располагаются вне контуров изображений, приведенных на чертеже (рис. 4.2) (выносятся на любое свободное место чертежа).

Наложенные сечения вычерчиваются сплошными тонкими линиями и располагаются в том месте, где проходила секущая плоскость, и непосредственно на самом виде, т.е. накладываются на изображение (рис.4.3).

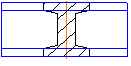
Рис. 4.3

Вынесенным сечениям следует отдавать предпочтение перед наложенными, так как наложенные затемняют виды чертежа и неудобны для нанесения размеров.

Вынесенное сечение можно располагать, в зависимости от обстоятельств, на любом месте поля чертежа. Оно может быть помещено непосредственно на продолжении линии сечения в проекционной связи (рис.4.4), с нарушением проекционной связи (рис.4.6), а также в разрыве между частями одного и того же вида (рис.4.5).

Рис.4.4

Рис.4.5

Рис.4.6

4.3. Отличие разреза от сечения.

Сечение отличается от разреза тем, что в разрезе изображается то, что расположено в секущей плоскости и то, что расположено за ней, а в сечении показывается только то, что попало непосредственно в секущую плоскость.

На рисунке 4.7 а показан разрез детали. На нем изображено то, что попало в секущую плоскость А-А , и то что расположено за ней. На рисунке 4.7 б показано сечение А-А .

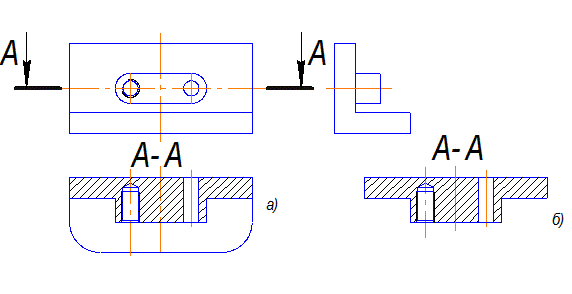
Рис. 4.7

4.4. Обозначение сечений.

Сечения на чертежах обозначаются по такому же принципу, как и разрезы. Секущая плоскость изображается разомкнутой линией.

Каждую плоскость обозначают у начала и конца разомкнутой линии наружи от стрелки одной и той же прописной буквой русского алфавита.

Если секущая плоскость совпадает с осью симметрии наложенного или вынесенного сечения, то ее проводят штрихпунктирной тонкой линией и не обозначают буквами и стрелками (рис.4.3, 4.4,4.5). Над сечением в этих случаях не делают никакой надписи.

Сечение можно располагать повернутым. Тогда к надписи должен быть добавлен знак (рис.4.6).

4.5 Некоторые правила построения сечений.

Для нескольких одинаковых сечений, относящихся к одному и тому же предмету, следует линии сечения обозначать одной и той же буквой и вычерчивать одно сечение (рис.4.8).

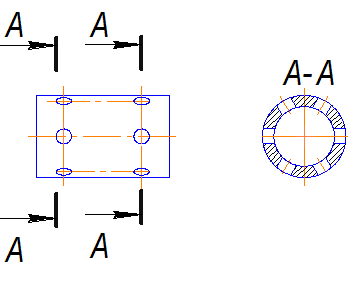
Рис.4.8

Если секущая плоскость проходит через ось поверхности вращения, что ограничивает отверстие или углубление; например, через конусообразное углубление или цилиндрическое сквозное отверстие (рис.4.2,4.7), то на фигуре сечения контур отверстия или углубления показывают по типу разреза. Однако нужно заметить, что это относится к изображениям отверстий и углублений, имеющих форму поверхности вращения (рис.4.9 б) и не распространяется на изображение отверстий другой формы (рис.4.9 а).

Рис. 4.9

Сечение обычно выполняют в том же масштабе, что и вид, к которому оно относится, Тогда отверстия, углубления и другие элементы, находящиеся на фигуре сечения, будут тех же размеров, что и на видах чертежа. Если же масштаб сечения изменен, то над изображением его указывают масштаб надписью по типу: А-А (2:1), Б-Б (1:2).

Сечение должно по построению и расположению соответствовать направлению, указанному стрелками. Выбирать направление проецирования для несимметричных сечений рекомендуется, исходя из следующего. Если секущая плоскость расположена вертикально, сечение обычно совмещается с плоскостью чертежа вращением слева направо (рис.4.9, 4.10); если же секущая плоскость проходит горизонтально, то вращением на себя (рис.4.7.). Сечения, как и разрезы, выполняют для выяснения внутреннего устройства предмета и простановки его внутренних размеров.

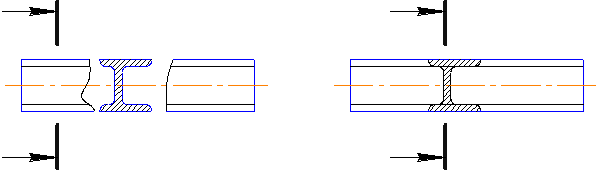
Рис. 4.10

5.Выносные элементы.

Выносной элемент - дополнительное отдельное увеличенное изображение какой-либо части предмета, требующей пояснений в отношении формы и размеров, а поэтому обычно выполняется в масштабе увеличения.

При применении выносного элемента соответствующее место отмечают на виде, разрезе или сечении замкнутой сплошной тонкой линией- окружностью, овалом и т.п. с обозначением прописной буквой русского алфавита или буквенно-цифровым. Над изображением выносного элемента наносят обозначение по типу: А(4:1 ) (рис.5.1).

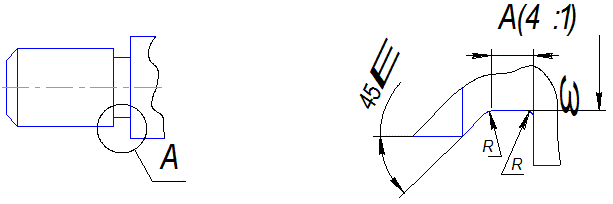
Рис. 5.1

6. Условности и упрощения, применяемые при выполнении изображений

При выполнении различных изображений применяют условности и упрощения, которые позволяют сократить объем графической работы, сохраняя ясность и наглядность изображений предметов.

6.1. Если вид, разрез или сечение представляют собой симметричную фигуру, допускается показывать половину изображения (рис. 6.1а) или немного более. В последнем случае проводится линия обрыва (рис.6.1б).


Рис. 6.1	Рис. 6.2	Рис.6.3

6.2. Если предмет имеет несколько одинаковых, равномерно расположенных элементов, то на изображении этого предмета полностью показывают один - два таких элемента, а остальные - упрощенно или условно (например, показывают центры отверстий) ( рис.6.2).

6.3. Для установления формы пазов на валах и других деталях допускается вместо вида всей детали показать только контур отверстий и пазов (рис.6.3).

6.4. При недостатке места предметы или элементы, имеющие постоянное или закономерно изменяющееся поперечное сечение (валы, цепи, прутки, фасонный прокат, шатуны и т. п.), допускается изображать с разрывами (рис. 6.4).

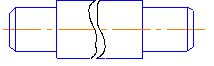
Рис.6.4

6.5 Болты ,винты, оси, валы не рассекаются в продольном разрезе.

6.6. Гайки, шайбы, шарики на сборочном чертеже показывают нерассеченными.

6.7 Такие элементы, как спицы, тонкие стенки типа ребер жесткости и т. п., показывают не заштрихованными, если секущая плоскость направлена вдоль оси или длинной стороны этого элемента (рис.6.5).

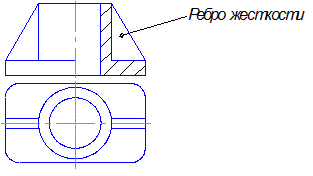
Рис. 6.5

Ответ на тест № 1: изображение разреза выполнено верно на фрагменте № 4.

Внимание! Тест № 2

Установите допущенные графические ошибки при выполнении данных изображений.

Ответы на тесты находятся на страницах

Ответы на тест № 2

7.Содержание заданий

7.1. Задание 1

1. По аксонометрическому изображению детали и заданным размерам начертить три ее вида - главный, сверху и слева. Наглядное изображение не перечерчивать.

2. Выполнить необходимые разрезы.

3. Построить линии пересечения поверхностей.

4. Нанести размерные линии и проставить размерные числа.

5. Выполнить обводку чертежа и заполнить основную надпись.

7.2. Задание 2

1. По размерам перечертить заданные два вида предмета и построить третий вид.

2. Выполнить необходимые разрезы.

3. Построить линии пересечения поверхностей.

4. Нанести размерные линии и проставить размерные числа.

5. Выполнить обводку чертежа и заполнить основную надпись.

7.3. Задание 3

1. По размерам перечертить заданные два вида предмета и построить третий вид.

2. Выполнить необходимые разрезы.

3. Построить линии пересечения поверхностей.

4. Нанести размерные линии и проставить размерные числа.

5. Выполнить обводку чертежа и заполнить основную надпись.

Для всех задач виды чертить только в проекционной связи.

7.1. Задача 1.

Рассмотрим примеры выполнения заданий.

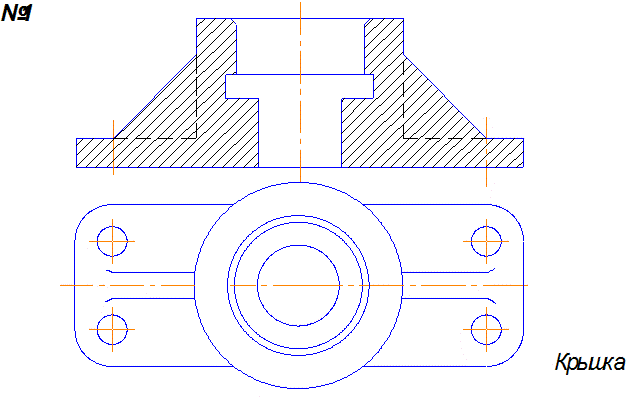
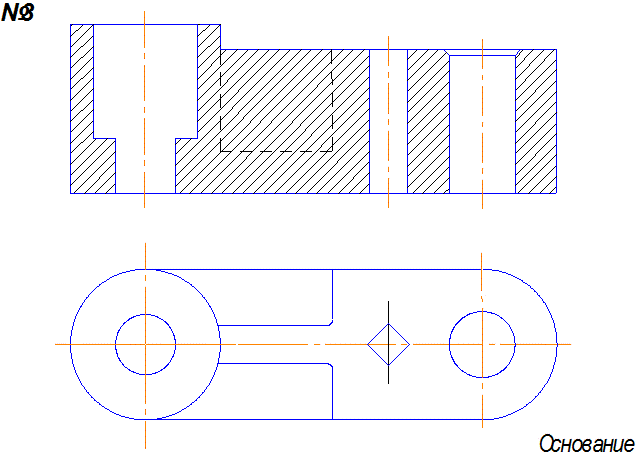
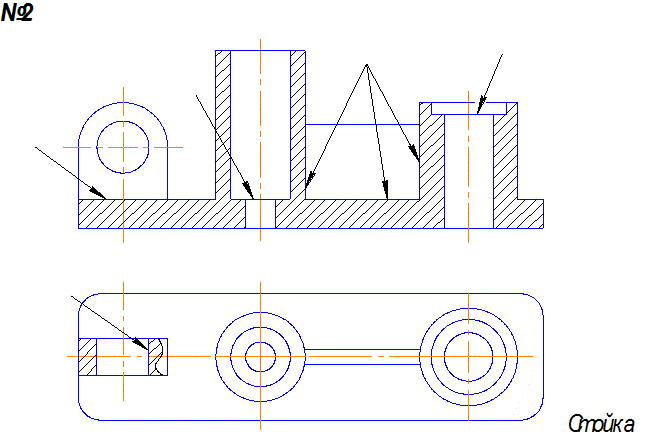
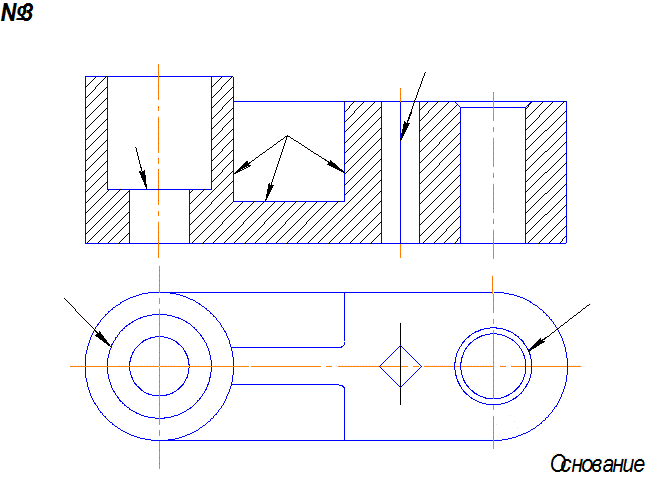
Задача1 . По наглядному изображению построить три вида детали и выполнить необходимые разрезы.

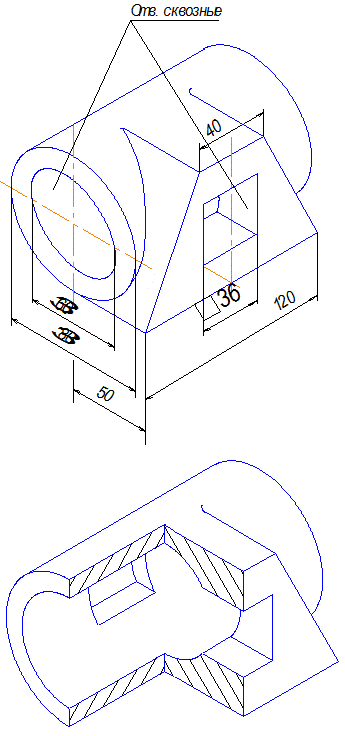
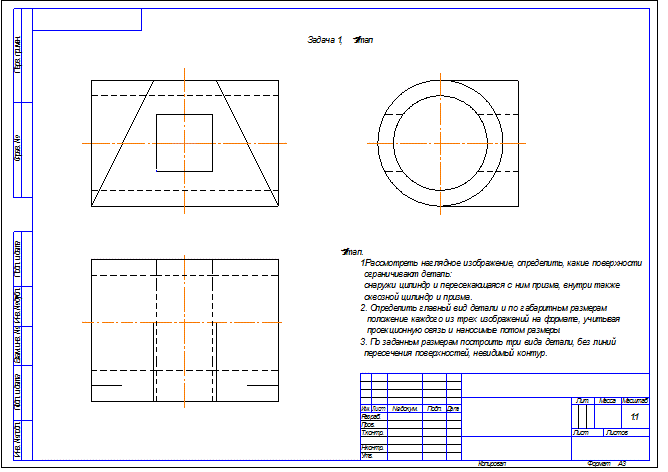
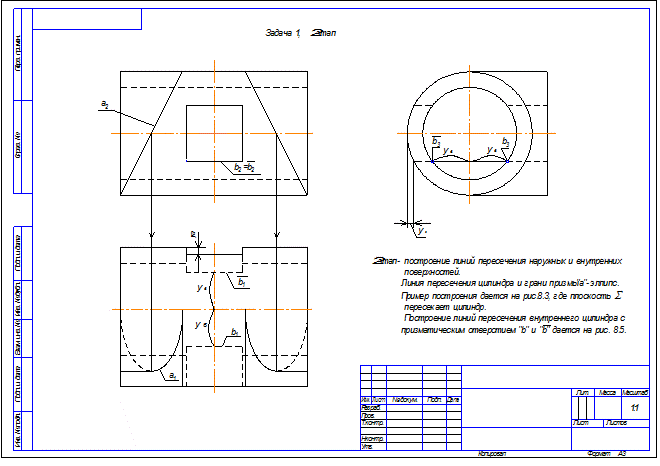
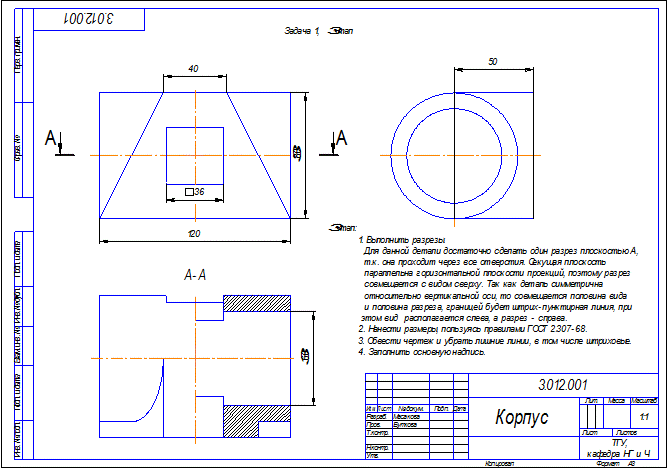
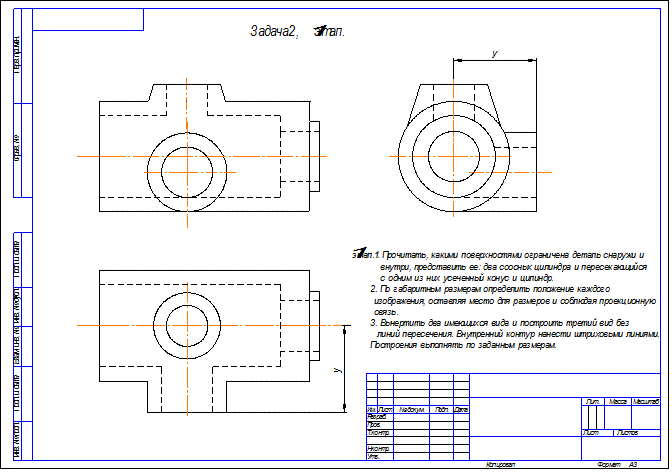
7.2 Задача 2

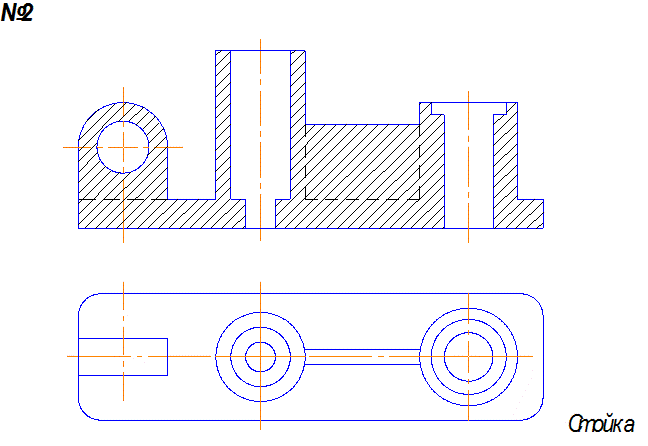
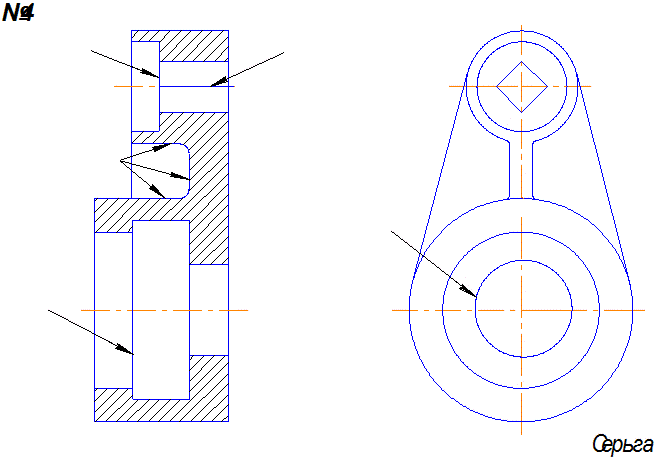
Задача2 . По двум видам построить третий вид и выполнить необходимые разрезы.

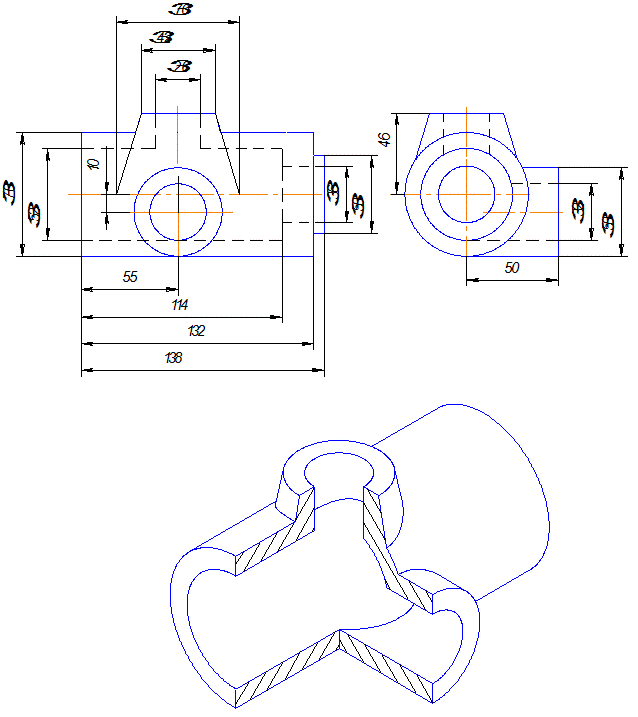
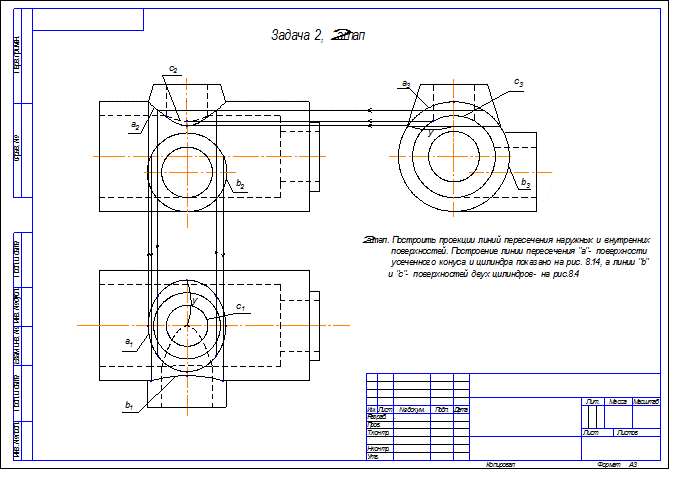
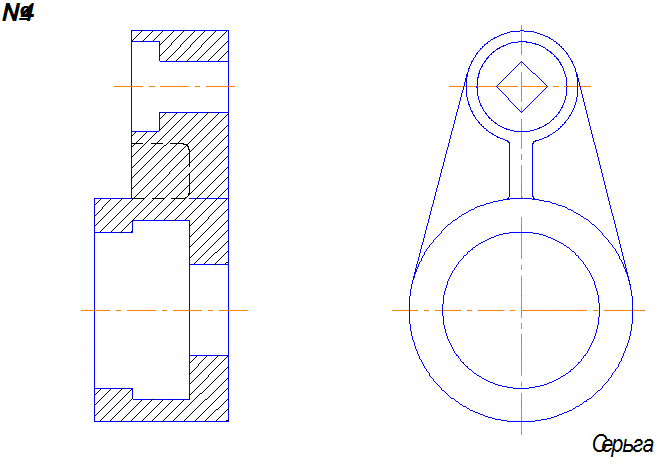
Задача 2. III этап.

1. Выполнить необходимые разрезы. Количество разрезов должно быть минимальным, но достаточным, чтобы прочитать внутренний контур.

1. Секущая плоскость А открывает внутренние соосные поверхности. Эта плоскость параллельна фронтальной плоскости проекций, поэтому разрез А-А совмещается с главным видом.

2. На виде слева показан местный разрез, открывающий цилиндрическое отверстие 32.

3. Размеры наносятся на тех изображениях, где поверхность читается лучше, т.е. диаметр, длина и т.д., например, 52 и длина 114.

4. Выносные линии по возможности не пересекать. Если главный вид выбран правильно, то наибольшее количество размеров будет на главном виде.

Проверить:

Чтобы каждый элемент детали имел достаточное количество размеров.
Чтобы все выступы и отверстия были привязаны размерами к другим элементам детали (размер 55, 46, и 50).
Габаритные размеры.
Выполнить обводку чертежа, убрав все линии невидимого контура. Заполнить основную надпись.

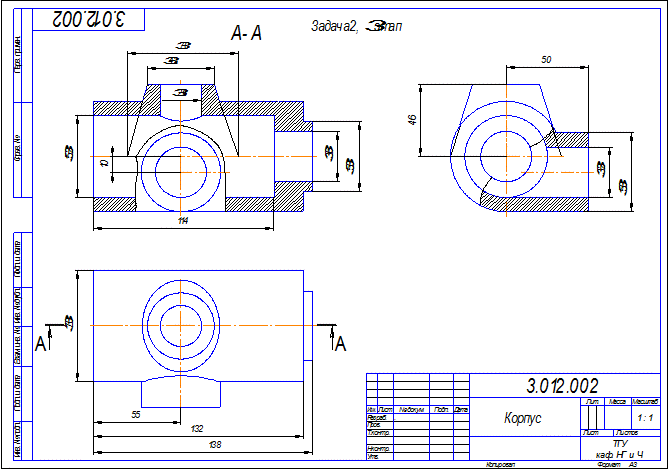
7.3. Задача 3.

Построить три вида детали и выполнить необходимые разрезы.

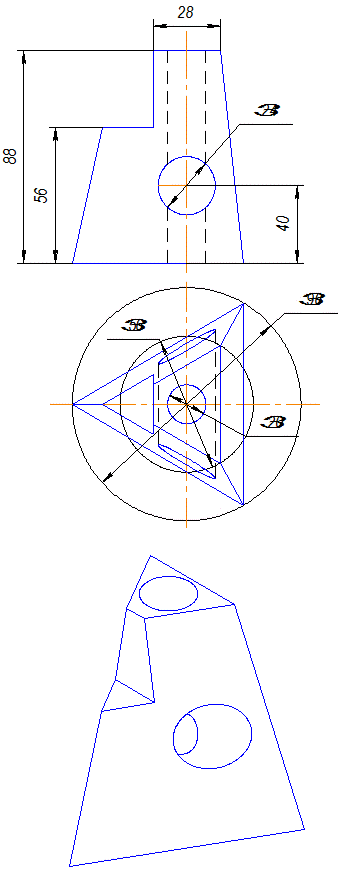
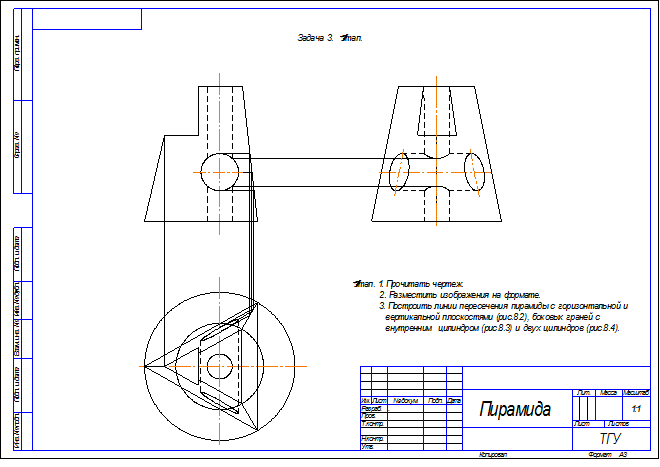
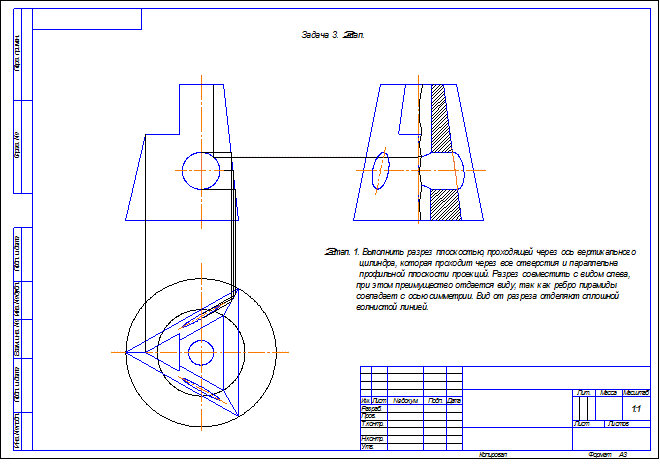
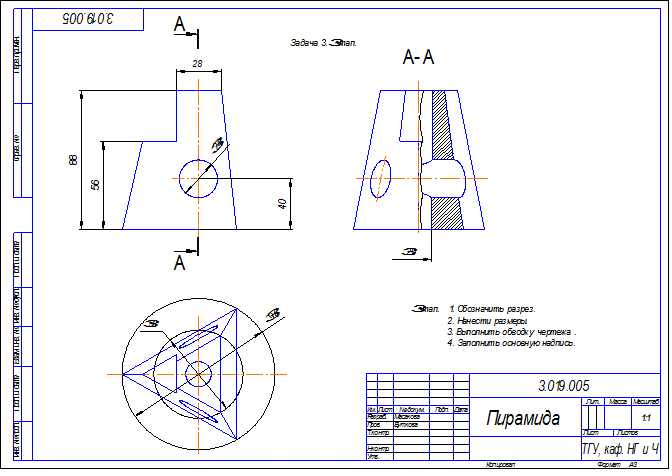
8. Сведения о поверхностях.

Построение линий, принадлежащих поверхностям.

Поверхности.

Для того, чтобы построить линии пересечения поверхностей, нужно уметь строить не только поверхности, но и точки, расположенные на них. В этом разделе рассматриваются наиболее часто встречающиеся поверхности.

8.1. Призма.

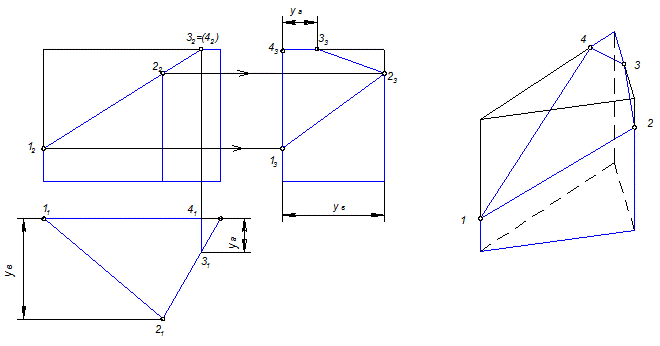
Рис. 8.1

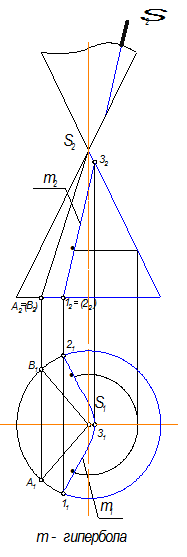
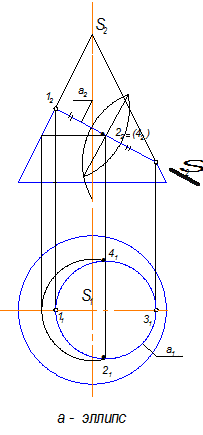
Задана трехгранная призма (рис.8.1), усеченная фронтально-проецирующей плоскостью (2ГПЗ, 1 алгоритм, модуль №3). S L= т (1234 )

Так как призма проецирующая относительно П₁ , то горизонтальная проекция линии пересечения уже есть на чертеже, она совпадает с главной проекцией заданной призмы.

Секущая плоскость проецирующая относительно П₂ , значит и фронтальная проекция линии пересечения есть на чертеже, она совпадает с фронтальной проекцией этой плоскости.

Профильная проекция линии пересечения строится по двум заданным проекциям.

8.2. Пирамида

Задана усеченная трехгранная пирамида Ф(S,АВС) (рис.8.2).

Данная пирамида F пересекается плоскостями S, D и Г .

2 ГПЗ, 2 алгоритм (Модуль №3).

Ф S = 123

S ^ П₂ S₂ = 1₂ 2₂ 3₂

1₁ 2₁ 3₁ и 1₃ 2₃ 3₃ строятся по принадлежности к поверхности Ф .

Ф D = 345

D ^ П₂ = 3₂ 4 ₂ 5 ₂

3₁ 4₁ 5₁ и 3₃ 4₃ 5₃ строятся по принадлежности к поверхности Ф .

Ф Г = 456

Г П₂ Г₂ = 4₂ 5 6

4₁ 5₁ 6₁ и 4₃ 5₃ 6₃ строятся по принадлежности к поверхности Ф .

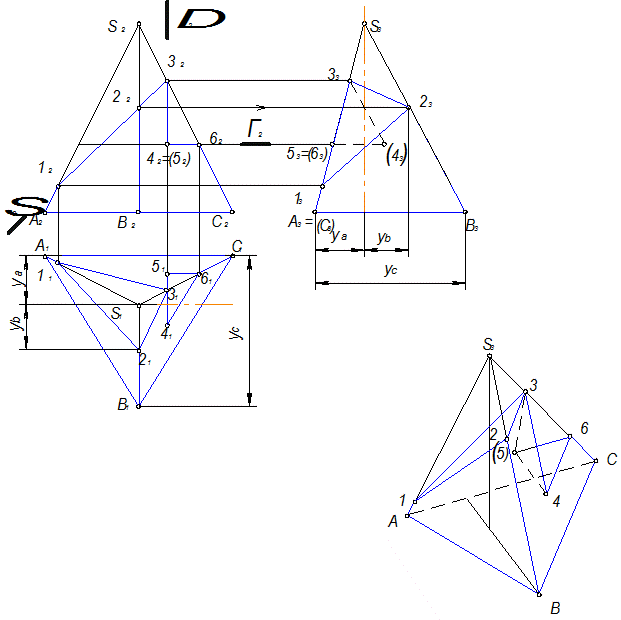
Рис. 8.2

8.3. Тела, ограниченные поверхностями вращения.

Телами вращения называют геометрические фигуры, ограниченные поверхностями вращения (шар, эллипсоид вращения, кольцо) или поверхностью вращения и одной или несколькими плоскостями (конус вращения, цилиндр вращения и т. д.). Изображения на плоскостях проекций, параллельных оси вращения, ограничены очерковыми линиями. Эти очерковые линии являются границей видимой и невидимой части геометрических тел. Поэтому при построении проекций линий, принадлежащих поверхностям вращения, необходимо строить точки, расположенные на очерках.

8.3.1. Цилиндр вращения.

Если ось вращения перпендикулярна П₁ , то на эту плоскость цилиндр будет проецироваться в виде окружности, а на две другие плоскости проекций в виде прямоугольников, ширина которых равна диаметру этой окружности. Такой цилиндр является проецирующим к П₁ .

Если ось вращения перпендикулярна П₂ , то на П₂ он будет проецироваться в виде окружности, а на П₁ и П₃ в виде прямоугольников.

Аналогичное рассуждение при положении оси вращения, перпендикулярном П₃ (рис.8.3).

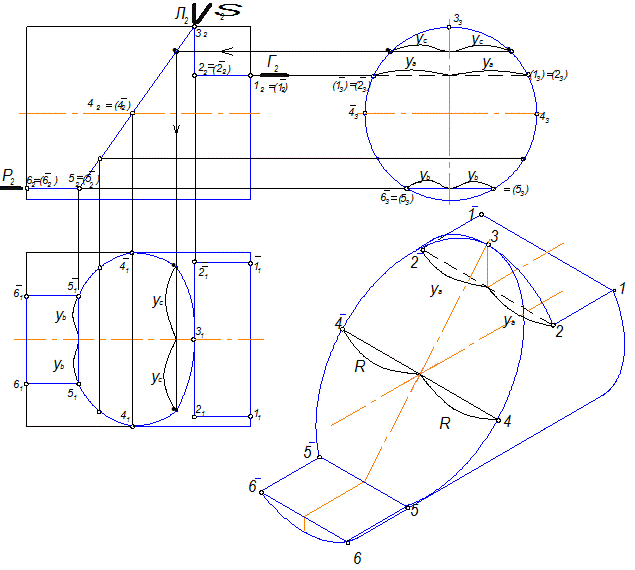
Рис.8.3

Цилиндр Ф пересекается с плоскостями Р , S , L и Г (рис.8.3).

2 ГПЗ, 1 алгоритм (Модуль №3)

Ф ^ П₃

Р, S, L, Г ^ П₂

Ф Р = а (6 5 и )

Ф ^ П₃ Ф₃ = а₃ (6₃ =5₃ и = )

а₂ и а₁ строятся по принадлежности к поверхности Ф .

Ф S = b (5 4 3 )

Ф S = с (2 3 ) Рассуждения аналогичны предыдущему.

Ф Г = d (12 и

Задачи на рисунках 8.4, 8.5, 8.6 решаются аналогично задаче на рис.8.3, так как цилиндр

везде профильно-проецирующий, а отверстия - поверхности проецирующие относительно

П₁ - 2ГПЗ, 1 алгоритм (Модуль №3).

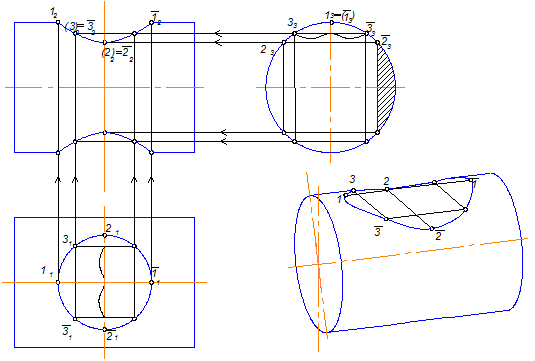
Рис. 8.4

Рис. 8.5

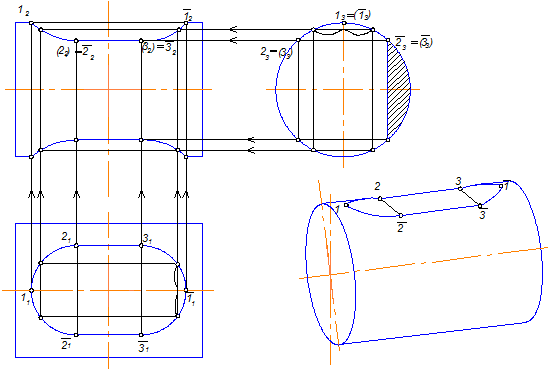
Рис. 8.6

Если оба цилиндра имеют одинаковые диаметры (рис.8.7), то линиями пересечения их будут два эллипса (теорема Монжа, модуль №3). Если оси вращения этих цилиндров лежат в плоскости, параллельной одной из плоскостей проекций, то на эту плоскость эллипсы будут проецироваться в виде пересекающихся отрезков прямых.

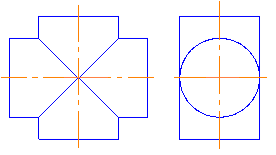
Рис. 8.7

8.3.2.Конус вращения

Задачи на рисунках 8.8, 8.9, 8.10, 8.11, 8.12 -2 ГПЗ (модуль №3) решаются по 2 алгоритму, так как поверхность конуса не может быть проецирующей, а секущие плоскости везде фронтально-проецирующие.

Рис. 8.8

Рис. 8.9

Рис. 8.10

Рис.8.11

Рис.8.12

На рисунке 8.13 изображен конус вращения (тело), пересеченный двумя фронтально-проецирующими плоскостями Г и L . Линии пересечения строят по 2 алгоритму.

На рисунке 8.14 поверхность конуса вращения пересекается с поверхностью профильно-проецирующего цилиндра.

2 ГПЗ, 2 алгоритм решения (модуль №3), то есть профильная проекция линии пересечения есть на чертеже, она совпадает с профильной проекцией цилиндра. Две другие проекции линии пересечения строят по принадлежности конусу вращения.

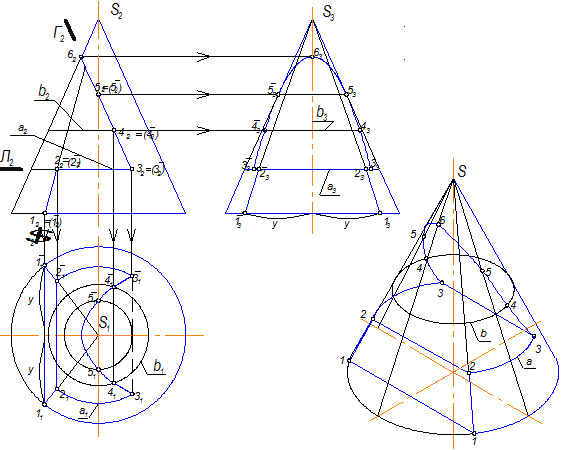
Рис.8.13

Рис.8.14

8.3.3. Сфера.

Поверхность сферы пересекается с плоскостью и со всеми поверхностями вращения с ней, по окружностям. Если эти окружности параллельны плоскостям проекций, то проецируются на них в окружность натуральной величины, а если не параллельны, то в виде эллипса.

Если оси вращения поверхностей пересекаются и параллельны одной из плоскостей проекций, то на эту плоскость все линии пересечения - окружности проецируются в виде отрезков прямых.

На рис. 8.15 - сфера, Г - плоскость, L - цилиндр, Ф - усеченный конус.

S Г = а - окружность;

S L =b - окружность;

S Ф =с - окружность.

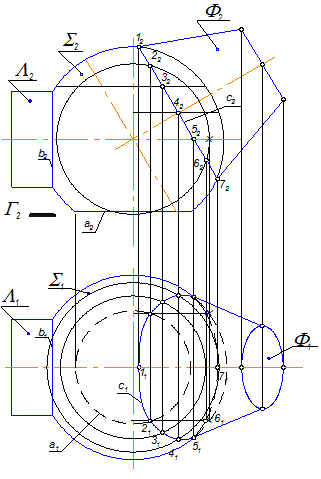
Рис.8.15

Так как оси вращения всех пересекающихся поверхностей параллельны П₂ , то все линии пересечения - окружности на П₂ проецируются в отрезки прямых.

На П₁ : окружность а проецируется в истинную величину так как параллельна ей; окружность b проецируется в отрезок прямой, так как параллельна П₃ ; окружностьс проецируется в виде эллипса, который строится по принадлежности сфере.

Сначала строятся точки 1, 7 и 4, которые определяют малую и большую оси эллипса. Затем строит точку 5 , как лежащую на экваторе сферы.

Для остальных точек (произвольных) проводят окружности (параллели) на поверхности сферы и по принадлежности им определяются горизонтальные проекции точек, лежащих на них.

9. Примеры выполнения заданий.

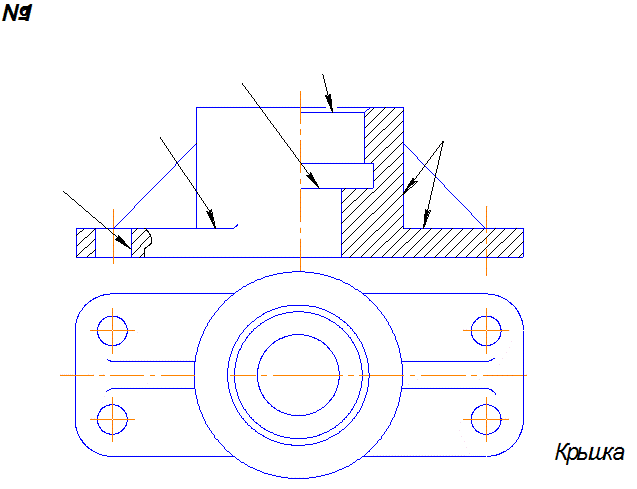
Задача 4 .Построить три вида детали с необходимыми разрезами и нанести размеры.

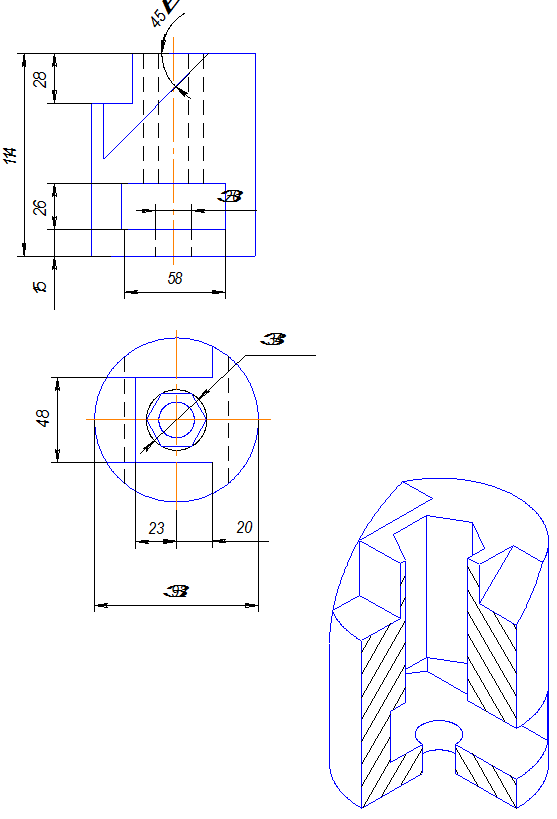
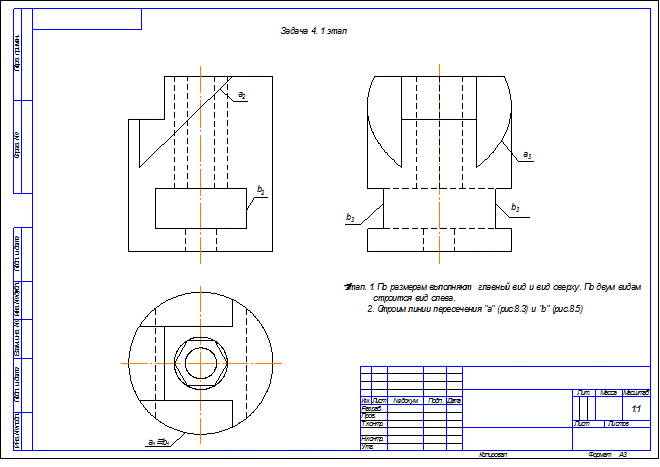
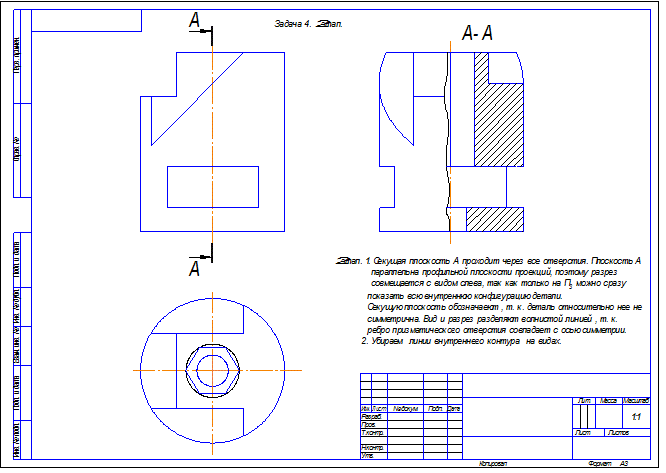
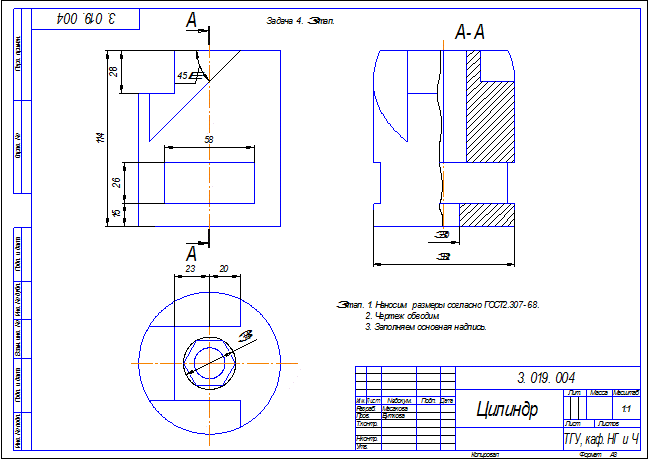
Задача 5. Построить три вида детали и выполнить необходимые разрезы.

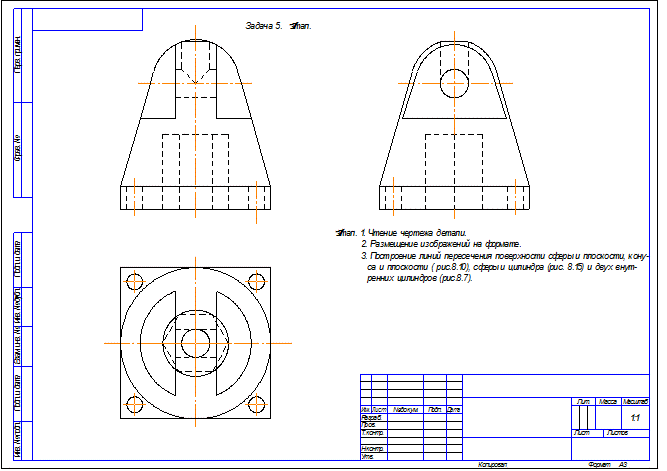
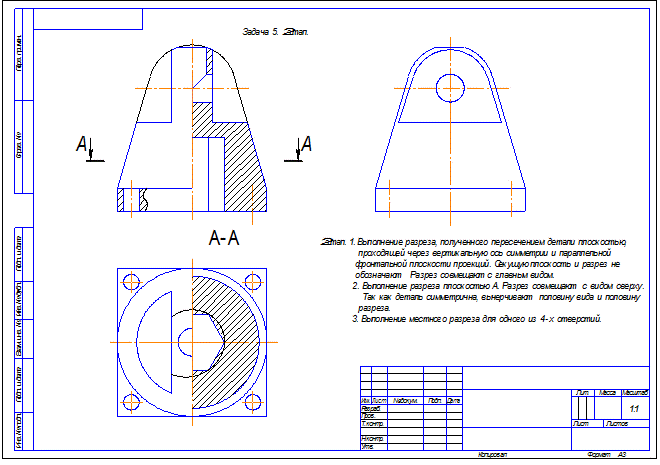
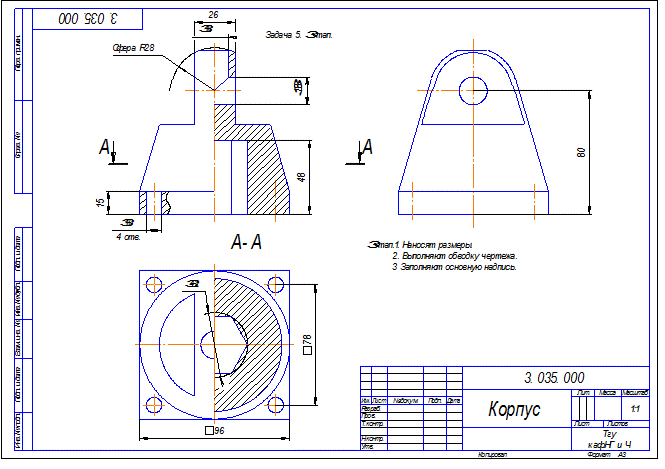
10.Аксонометрия

10.1. Краткие теоретические сведения об аксонометрических проекциях

Комплексный чертеж, составленный из двух или трех проекций, обладая свойствами обратимости, простоты и др., вместе с тем имеет существенный недостаток: ему недостает наглядности. Поэтому, желая дать более наглядное представление о предмете, наряду с комплексным чертежом приводят аксонометрический, широко используемый при описании конструкций изделий, в руководствах по эксплуатации, в схемах сборки, для пояснений чертежей машин, механизмов и их деталей.

Сравните два изображения - ортогональный чертеж и аксонометрический одной и той же модели. На каком изображении легче прочитать форму? Конечно на аксонометрическом изображении. (рис.10.1)

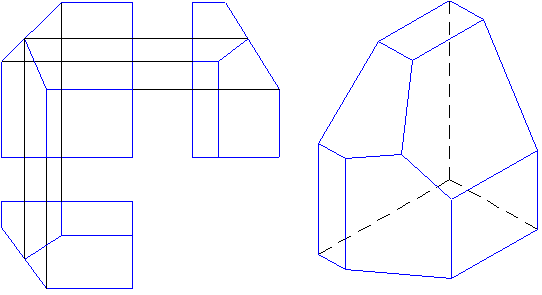
Рис.10.1

Сущность аксонометрического проецирования состоит в том, что геометрическая фигура вместе с осями прямоугольных координат, к которым она отнесена в пространстве, параллельно проецируется на некоторую плоскость проекций, называемую аксонометрическая плоскость проекций, или картинная плоскость.

Если отложить на осях координат x,y и z отрезок l (lx,ly,lz ) и спроецировать на плоскость П , то получим аксонометрические оси и на них отрезки lx, ly, lz (рис.10.2)

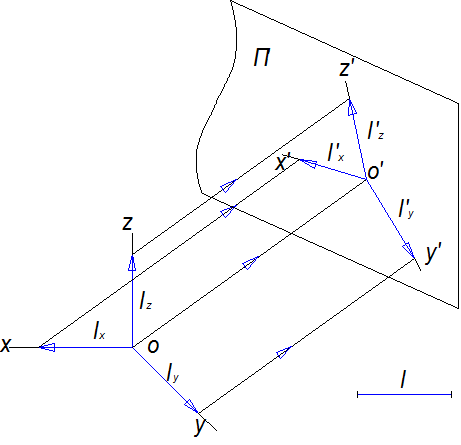
Рис.10.2

lx, ly, lz - натуральные масштабы.

l = lx = ly = lz

lx, ly, lz - аксонометрические масштабы.

Полученную совокупность проекций на П называют аксонометрией.

Отношение длины аксонометрических масштабных отрезков к длине натуральных масштабных отрезков называют показателем или коэффициентом искажения по осям, которые обозначаются Кx, Ky, Kz.

Kx = ;

Ky = ;

Kz=

Виды аксонометрических изображений зависят:

1. От направления проецирующих лучей (они могут быть перпендикулярны П - тогда аксонометрия будет называться ортогональной (прямоугольной) или расположены под углом не равным 90°- косоугольная аксонометрия).

2. От положения осей координат к аксонометрической плоскости.

Здесь возможны три случая: когда все три оси координат составляют с аксонометрической плоскостью проекций некоторые острые углы (равные и неравные) и когда одна или две оси ей параллельны.

В первом случае применяется только прямоугольное проецирование, (s ^ П) во втором и третьем - только косоугольное проецирование (s П) .

Если оси координат ОХ, ОY,OZ не параллельны аксонометрической плоскости проекций П , то будут ли они проецироваться на нее в натуральную величину? Конечно, нет. Изображение прямых в общем случае всегда меньше натуральной величины.

Рассмотрим ортогональный чертеж точки А и ее аксонометрическое изображение.

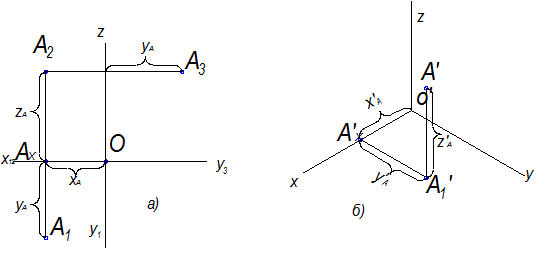
Рис.10.3

Положение точки определяют три координаты – Х_А , Y_А , Z_A , полученные путем измерения звеньев натуральной ломаной ОА_Х - А_Х А₁ – А₁ А (рис.10.3).

A - главная аксонометрическая проекция точки А ;

А - вторичная проекция точки А (проекция проекции точки).

Коэффициентами искажения по осям Х, Y и Z будут:

k_x = ; k_y = ; k_y =

В ортогональной аксонометрии эти показатели равны косинусам углов наклона осей координат к аксонометрической плоскости, а следовательно, они всегда меньше единицы.

Их связывает формула

k² _x + k² _y + k² _z = 2 (I)

В косоугольной аксонометрии показатели искажения связаны формулой

k_x + k_y + k_z = 2+ctg a (III)

т.е. любой из них может быть меньше, равен или больше единицы (здесь a- угол наклона проецирующих лучей к аксонометрической плоскости). Обе формулы - вывод из теоремы Польке.

Теорема Польке: аксонометрические оси на плоскости чертежа (П) и масштабы на них могут быть выбраны совершенно произвольно.

(Следовательно, аксонометрическая система (О X Y Z ) в общем случае определяется пятью независимыми параметрами: тремя аксонометрическими масштабами и двумя углами между аксонометрическими осями).

Углы наклона натуральных осей координат к аксонометрической плоскости проекций и направление проецирования могут быть выбраны произвольно, следовательно возможно множество видов ортогональных и косоугольных аксонометрий.

Их разделяют на три группы:

1. Все три показателя искажения равны (k_x = k_y = k_z ). Этот вид аксонометрии называют изометрией . 3k² =2; k= » 0,82 - теоретический коэффициент искажения. Согласно ГОСТ 2.317-70 можно пользоваться К=1 - приведенный коэффициент искажения.

2. Два каких-либо показателя равны (например, kx=ky kz). Этот вид аксонометрии называется диметрией . k_x = k_z ; k_y = 1/2k_x ² ; k_x ² +k_z ² + k_y ² /4 = 2; k = » 0,94; k_x = 0,94; ky = 0,47; kz = 0,94 - теоретические коэффициенты искажения. Согласно ГОСТ 2.317-70 коэффициенты искажения могут быть приведенными - k_x =1; k_y =0,5; k_z =1.

3. 3. Все три показателя различны (k_x k_y k_z ). Этот вид аксонометрии называют триметрией .

На практике применяют несколько видов как прямоугольной, так и косоугольной аксонометрии с наиболее простыми соотношениями между показателями искажений.

10.2. Рекомендации по выбору аксонометрических проекций

Из ГОСТ2.317-70 и различных видов аксонометрических проекций рассмотрим ортогональные изометрию и диметрию, а также косоугольную диметрию, как наиболее часто применяющиеся.

10.2.1. Прямоугольная изометрия

В изометрии все оси наклонены к аксонометрической плоскости под одним и тем же углом, следовательно угол между осями (120° ) и коэффициент искажения будет одинаков. Выбираем масштаб 1 : 0,82=1,22; М 1,22 : 1.

Для удобства построения пользуются приведенными коэффициентами и тогда на всех осях и линиях им параллельных откладываются натуральные размеры. Изображения таким образом становятся больше, но на наглядности это не отражается.

Выбор вида аксонометрии зависит от формы изображаемой детали. Проще всего строить прямоугольную изометрию, поэтому такие изображения встречаются чаще. Однако, при изображении деталей, включающих четырехугольные призмы и пирамиды, их наглядность уменьшается. В этих случаях лучше выполнять прямоугольную диметрию.

Косоугольную диметрию следует выбирать для деталей, имеющих большую длину при небольшой высоте и ширине (типа вала) или когда одна из сторон детали содержит наибольшее число важных особенностей.

В аксонометрических проекциях сохраняются все свойства параллельных проекций.

Рассмотрим построение плоской фигуры АВСDE .

Рис.10.4

Прежде всего построим оси в аксонометрии. На рис.10.4 представлено два способа построения аксонометрических осей в изометрии. На рис.10.4 а показано построение осей при помощи циркуля, а на рис.10.4б - построение при помощи равных отрезков.

Далее рассмотрим построение плоской фигуры АВСDE на плоском чертеже (рис.10.5а ) и в аксонометрии (рис.10.5б )

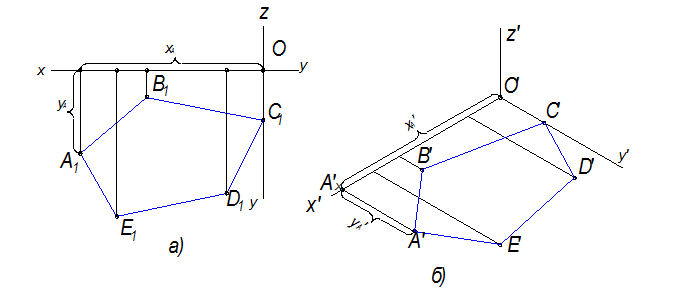Рис.10.5

Фигура АВСDЕ лежит в горизонтальной плоскости проекций, которая ограничена осями ОХ и ОY (рис.10.5а). Строим эту фигуру в аксонометрии (рис.10.5б).

Каждая точка, лежащая в плоскости проекций, сколько имеет координат? Две.

Точка, лежащая в горизонтальной плоскости - координаты Х и Y .

Рассмотрим построение т.А . С какой координаты начнем построение? С координаты Х_А .

Для этого замеряем на ортогональном чертеже величину ОА_Х и откладываем на оси Х , получим точку А_Х . А_Х А₁ какой оси параллельна? Оси Y . Значит из т. А_Х проводим прямую параллельную оси Y и откладываем на ней координату Y_A . Полученная точка А и будет аксонометрической проекцией т.А .

Аналогично строятся все остальные точки. Точка С лежит на оси ОY , значит имеет одну координату.

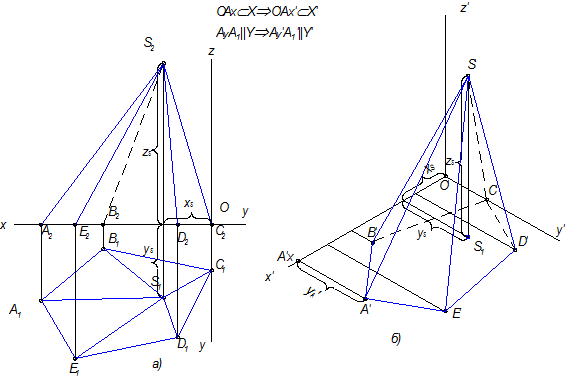
Рис.10.6

На рисунке 10.6 задана пятигранная пирамида, у которой основанием является этот же пятиугольник АВСDЕ. Что нужно достроить, чтобы получилась пирамида? Надо достроить точку S , которая является ее вершиной.

Точка S - точка пространства, поэтому имеет три координаты Х_S , Y_S и Z_S . Сначала строится вторичная проекция S (S₁ ), а затем все три размера переносятся с ортогонального чертежа. Соединив S c A, B, C, D и E , получим аксонометрическое изображение объемной фигуры - пирамиды.

10.2.2. Изометрия окружности

Окружности проецируются на плоскость проекций в натуральную величину, когда они параллельны этой плоскости. А так как все плоскости наклонены к аксонометрической плоскости, то окружности, лежащие на них, будут проецироваться на эту плоскость в виде эллипсов. Во всех видах аксонометрий эллипсы заменяются овалами.

При изображении овалов надо, прежде всего, обратить внимание на построение большой и малой оси. Начинать надо с определения положения малой оси, а большая ось всегда ей перпендикулярна.

Существует правило: малая ось совпадает с перпендикуляром к этой плоскости, а большая ось ей перпендикулярна или направление малой оси совпадает с осью, не существующей в этой плоскости, а большая ей перпендикулярна (рис.10.7)

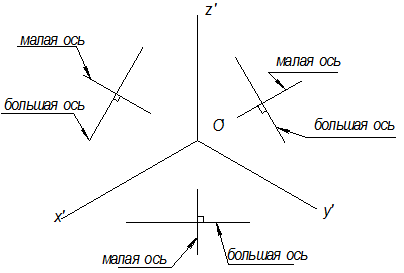
Рис.10.7

Большая ось эллипса перпендикулярна той координатной оси, которая отсутствует в плоскости окружности.

Большая ось эллипса равна 1,22 d _окр ; малая ось эллипса равна 0,71 d _окр .

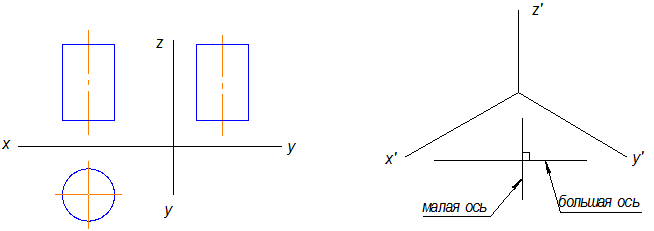
Рис.10.8

На рисунке 10.8 в плоскости окружности отсутствует ось Z , поэтому большая ось перпендикулярна оси Z .

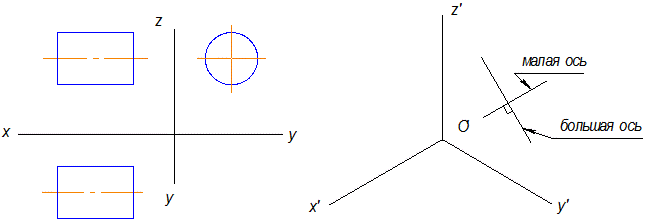
Рис.10.9

На рисунке 10.9 в плоскости окружности отсутствует ось Х , поэтому большая ось перпендикулярна оси Х .

А теперь рассмотрим, как вычерчивается овал в одной из плоскостей, например, в горизонтальной плоскости XY . Существует множество способов построения овала, познакомимся с одним из них.

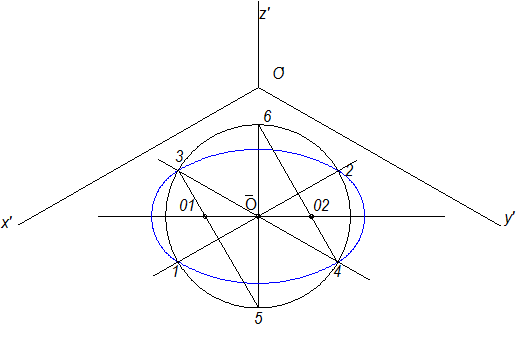
Рис.10.10

Последовательность построения овала следующая (рис.10.10):

1. Определяется положение малой и большой оси.

2.Через точку пересечения малой и большой оси проводим линии, параллельные осям X и Y .

3.На этих линиях, а также на малой оси, из центра радиусом, равным радиусу заданной окружности, откладываем точки 1 и 2, 3 и 4, 5 и 6 .

4. Соединяем точки 3 и 5, 4 и 6 и отмечаем точки пересечения их с большой осью эллипса (01 и 02 ). Из точки 5 , радиусом 5-3 , и из точки 6 , радиусом 6-4 , проводим дуги между точками 3 и 2 и точками 4 и 1 .

5. Радиусом 01-3 проводим дугу, соединяющую точки 3 и 1 и радиусом 02-4 - точки 2 и 4 . Аналогично строятся овалы в других плоскостях (рис.10.11).

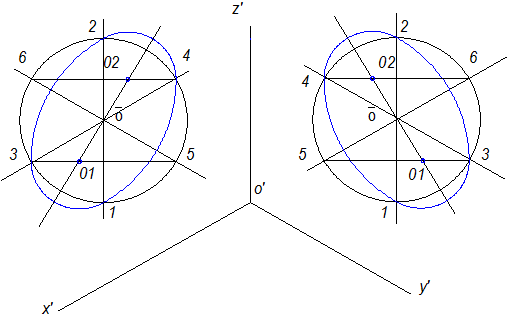
Рис.10. 11

Далее рассмотрим примеры построения аксонометрии конуса вращения и цилиндра.

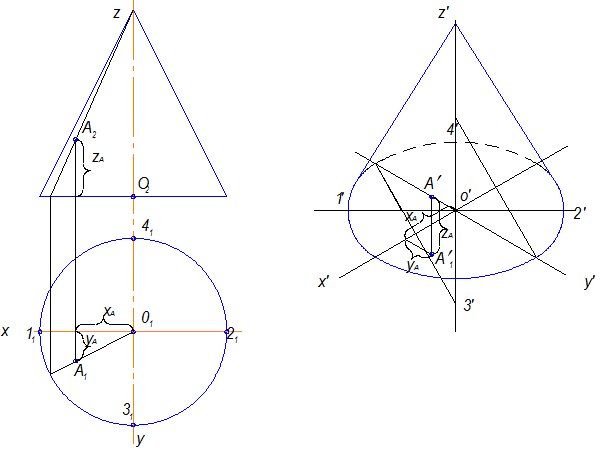
Рис.10.12

Для простоты построения наглядного изображения поверхности ось Z может совпадать с высотой поверхности, а оси X и Y с осями горизонтальной проекции.

Чтобы построить точку А , принадлежащую поверхности надо построить ее три координаты X_A , Y_A и Z_A . Точка на поверхности цилиндра и других поверхностях строится аналогично (рис.10.13).

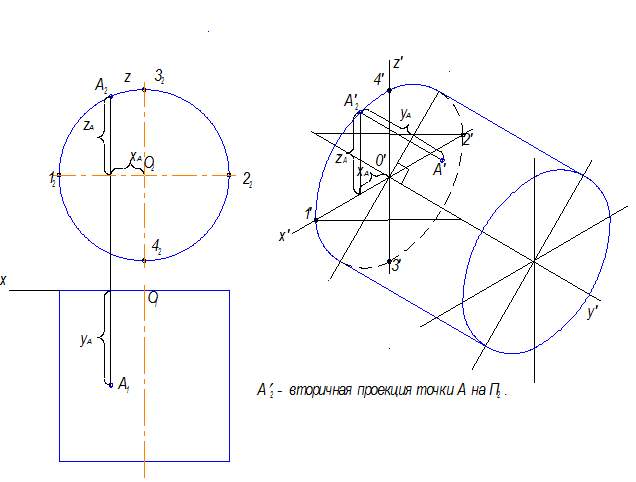
Рис.10.13

Большая ось овала перпендикулярна оси Y .

При построении аксонометрии детали, ограниченной несколькими поверхностями, следует придерживаться следующей последовательности:

Вариант 1.

1. Деталь мысленно разбивается на элементарные геометрические фигуры.

2. Вычерчивается аксонометрия каждой поверхности, линии построения сохраняются.

3. Строится вырез 1/4 детали, чтобы показать внутреннюю конфигурацию детали.

4. Наносится штриховка по ГОСТ 2.317-70.

Рассмотрим пример построения аксонометрии детали, внешний контур которой состоит из нескольких призм, а внутри детали цилиндрические отверстия разных диаметров.

Вариант 2. (Рис. 10.5)

1. Строится вторичная проекция детали на плоскости проекций П .

2. Откладываются высоты всех точек.

3. Строится вырез 1/4 части детали.

4. Наносится штриховка.

Для данной детали более удобным для построения будет вариант 1.

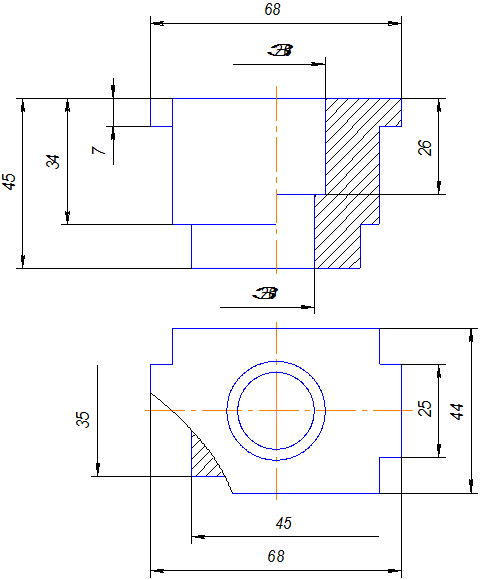
Рис.10.14

10.3. Этапы выполнения наглядного изображения детали.

1. Деталь вписывается в поверхность четырехугольной призмы, размеры которой равны габаритным размерам детали. Эта поверхность называется обертывающей.

Выполняется изометрическое изображение этой поверхности. Обертывающая поверхность строится по габаритным размерам (рис.10.15 а ).

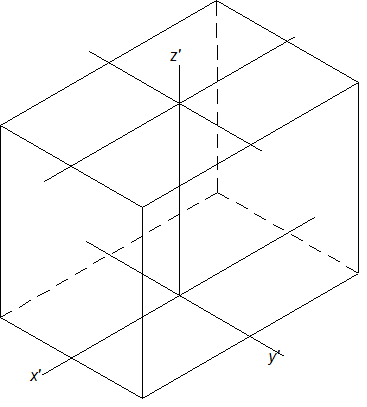
Рис. 10.15 а

2. Из этой поверхности вырезаются выступы, расположенные на верхней части детали по оси Х и строится призма высотой 34мм, одним из оснований которой будет верхняя плоскость обертывающей поверхности (рис.10.15б ).

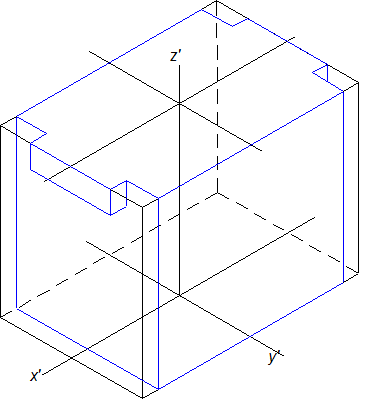
Рис. 10.15б

3. Из оставшейся призмы вырезается нижняя призма с основаниями 45 35 и высотой 11мм (рис.10.15в ).

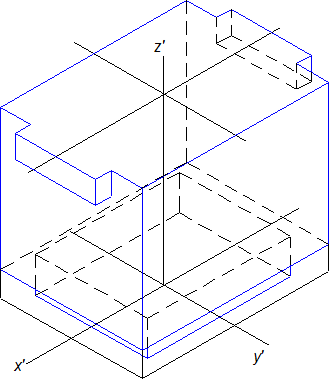
Рис. 10.15в

4. Строятся два цилиндрических отверстия, оси которых лежат на оси Z . Верхнее основание большого цилиндра лежит на верхнем основании детали, второе ниже на 26 мм. Нижнее основание большого цилиндра и верхнее основание малого лежат в одной плоскости. Нижнее основание малого цилиндра строится на нижнем основании детали (рис.10.15г ).

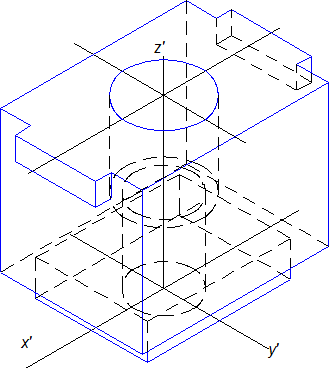
Рис. 10.15г

5. Выполняется вырез 1/4 части детали, чтобы открыть внутренний контур ее. Разрез выполняется двумя взаимно перпендикулярными плоскостями, то есть по осям Х и Y (рис.10.15д ).

Рис.10.15д

6. Выполняется обводка сечений и всей оставшейся части детали, а вырезанная часть убирается. Невидимые линии стираются, а сечения заштриховываются. Плотность штриховки должна быть такой же, как на ортогональном чертеже. Направление штриховых линий показано на рис10.15е соответствии с ГОСТ 2.317-69.

Линиями штриховки будут линии, параллельные диагоналям квадратов, лежащих в каждой координатной плоскости, стороны которых параллельны аксонометрическим осям.

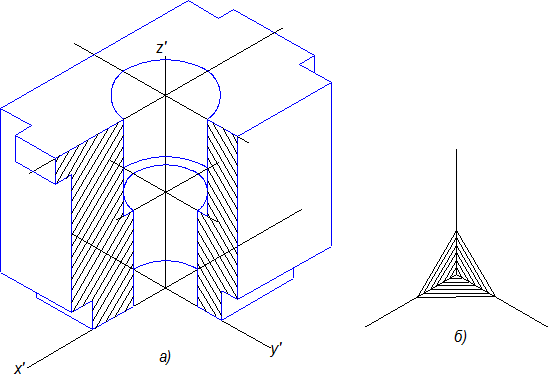
Рис.10.15е

7. Существует особенность штриховки ребра жесткости в аксонометрии. По правилам

ГОСТ 2.305-68 в продольном разрезе ребро жесткости на ортогональном чертеже не

заштриховывается, а в аксонометрии заштриховывается .На рис.10.16 показан пример

штриховки ребра жесткости.

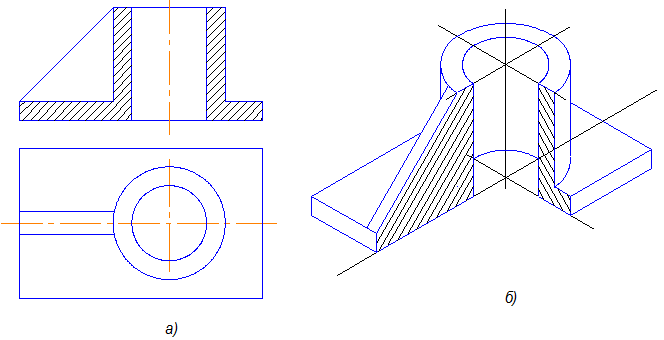
Рис. 10.16

10.4Прямоугольная диметрия.

Прямоугольную диметрическую проекцию можно получить путем поворота и наклона координатных осей относительно П так, чтобы показатели искажения по осям X и Z приняли равное значение, а по оси Y - вдвое меньшее. Показатели искажения k_x и k_z будут равны 0,94, а k_y - 0,47.

На практике пользуются приведенными показателями, т.е. по осям X и Z откладывают натуральные размеры, а по оси Y - в 2 раза меньше натуральных.

Ось Z обычно располагают вертикально, ось X - под углом 7°10 к горизонтальной линии, а ось Y -под углом 41°25 к этой же линии (рис.12.17).

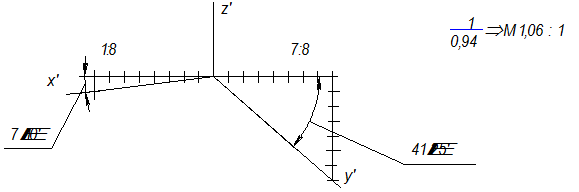
Рис. 12.17

1. Строится вторичная проекция усеченной пирамиды.

2. Строятся высоты точек 1,2,3 и 4.

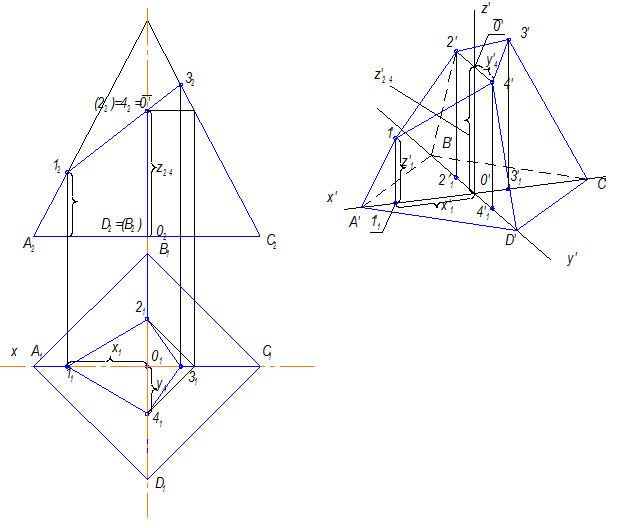
Рис. 10.18

Проще всего строить ось Х , отложив на горизонтальной линии 8 равных частей и вниз по вертикальной линии 1 такую же часть.

Чтобы построить ось Y под углом 41°25 , надо на горизонтальной линии отложить 8 частей, а на вертикальной 7 таких же частей (рис.10.17).

На рисунке 10.18 изображена усеченная четырехугольная пирамида. Чтобы построение ее в аксонометрии было проще, ось Z должна совпадать с высотой, тогда вершины основания ABCD будут лежат на осях Х и Y (А и С х , В и D y ). Сколько координат имеют точки 1 и ? Две. Какие? Х и Z .

Эти координаты откладываются в натуральную величину. Полученные точки 1 и 3 соединяются с точками А и С .

Точки 2 и 4 имеют две координаты Z и Y . Так как высота у них одинаковая, то координата Z откладывается на оси Z . Через полученную точку 0 проводится линия, параллельная оси Y , на которой по обе стороны от точки откладываются расстояние 0₁ 4₁ уменьшенное в два раза.

Полученные точки 2 и 4 соединяются с точками В и D .

10.4.1. Построение окружностей в прямоугольной диметрии.

Окружности, лежащие на плоскостях координат в прямоугольной диметрии, также как и в изометрии, будут изображаться в виде эллипсов. Эллипсы, расположенные на плоскостях между осями Х и Y,Y и Z в приведенной диметрии будут иметь большую ось, равную 1,06d, а малую - 0,35d, а в плоскости между осями X и Z - большую ось тоже 1,06d, а малую 0,95d (рис.10.19).

Эллипсы заменяются четырехцентовыми овалами, как в изометрии.

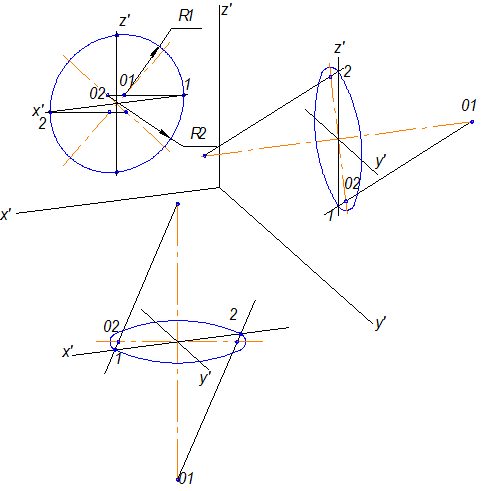
Рис.10.19

10.5.Косоугольная диметрическая проекция (фронтальная)

Если расположить координатные оси Х и Y параллельно плоскости П, то показатели искажения по этим осям станут равным единице (к = т =1). Показатель искажения по оси Y обычно принимают равным 0,5. Аксонометрические оси X и Z составят прямой угол, ось Y обычно проводят как биссектрису этого угла. Ось Х может быть направлена как вправо от оси Z , так и влево.

Предпочтительно пользоваться правой системой, так как удобнее изображать предметы в рассеченном виде. В этом виде аксонометрии хорошо чертить детали, имеющие форму цилиндра или конуса.

Рис. 10.20

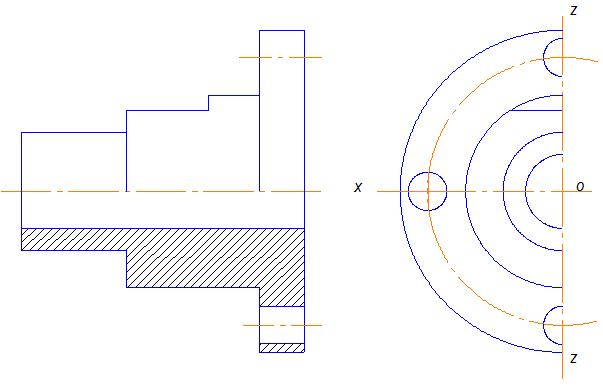
Рис.10.21

Для удобства изображения этой детали ось Y надо совместить с осью вращения поверхностей цилиндров. Тогда все окружности будут изображаться в натуральную величину, а длина каждой поверхности будет уменьшаться в два раза (рис.10.21).

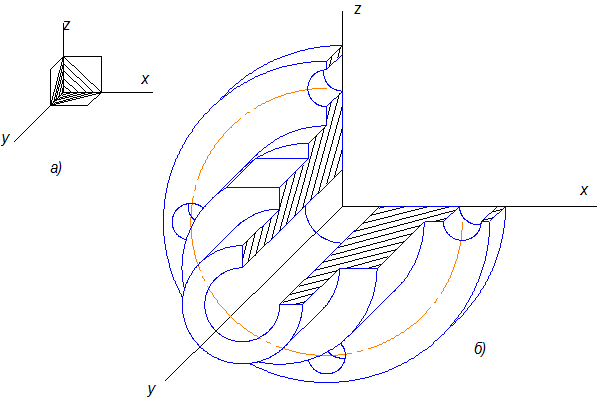
Рис. 10.22

11.Наклонные сечения.

При выполнении чертежей деталей машин приходится нередко применять наклонные сечения.

При решении таких задач необходимо прежде всего уяснить: как должна быть расположена секущая плоскость и какие поверхности участвуют в сечении для того, чтобы деталь читалась лучше. Рассмотрим примеры.

Дана четырехгранная пирамида, которая рассекается наклонной фронтально-проецирующей плоскостью А-А (рис.11.1). Сечением будет четырехугольник.

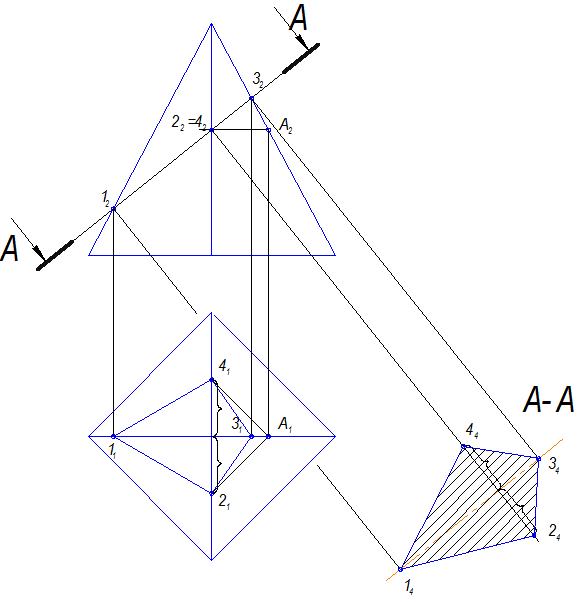
Рис. 11.1

Сначала строим проекции его на П₁ и на П₂ . Фронтальная проекция совпадает с проекцией плоскости, а горизонтальную проекцию четырехугольника строим по принадлежности пирамиде.

Затем строим натуральную величину сечения. Для этого вводится дополнительная плоскость проекций П₄ , параллельная заданной секущей плоскости А-А , на нее проецируем четырехугольник, а затем совмещаем его с плоскостью чертежа.

Эта четвертая основная задача преобразования комплексного чертежа (модуль №4, стр.15 или задача №117 из рабочей тетради по начертательной геометрии).

Построения выполняются в следующей последовательности (рис.11.2):

1. 1.На свободном месте чертежа проводим осевую линию, параллельную плоскости А-А .

2. 2.Из точек пересечения ребер пирамиды с плоскостью проводим проецирующие лучи, перпендикулярно секущей плоскости. Точки 1 и 3 будут лежать на линии, расположенной перпендикулярно осевой.

3. 3.Расстояние между точками 2 и 4 переносится с горизонтальной проекции.

4. Аналогично строится истинная величина сечения поверхности вращения - эллипс.

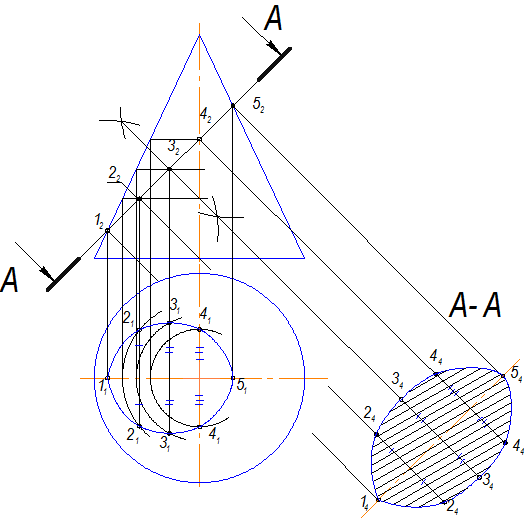
Рис. 11.2

Расстояние между точками 1 и 5 -большая ось эллипса. Малую ось эллипса надо строить путем деления большой оси пополам (3-3 ).

Расстояние между точками 2-2, 3-3, 4-4 переносятся с горизонтальной проекции.

Рассмотрим более сложный пример, включающий многогранные поверхности и поверхности вращения (рис.11.3)

Задана четырехгранная призма. В ней расположены два отверстия: призматическое, расположенное горизонтально и цилиндрическое, ось которого совпадает с высотой призмы.

Секущая плоскость фронтально-проецирующая, поэтому фронтальная проекция сечения совпадает с проекцией этой плоскости.

Четырехугольная призма проецирующая к горизонтальной плоскости проекций, а значит и горизонтальная проекция сечения тоже есть на чертеже, она совпадает с горизонтальной проекцией призмы.

Натуральная величина сечения, в которое попадают обе призмы и цилиндр, строим на плоскости, параллельной секущей плоскости А-А (рис.11.3).

Последовательность выполнения наклонного сечения:

1. Проводится ось сечения, параллельно секущей плоскости, на свободном поле чертежа.

2. Строится сечение наружной призмы: длина его переносится с фронтальной проекции, а расстояние между точками с горизонтальной.

3. Строится сечение цилиндра - часть эллипса. Сначала строятся характерные точки, определяющие длину малой и большой оси (5₄ , 2₄ -2₄ ) и точки, ограничивающие эллипс (1₄ -1₄ ) , затем дополнительные точки (4₄ -4₄ и 3₄ -3₄ ).

4. Строится сечение призматического отверстия.

5. Наносится штриховка под углом 45° к основной надписи, если она не совпадает с линиями контура, а если совпадает, то угол штриховки может быть 30° или 60°. Плотность штриховки на сечении такая же, как на ортогональном чертеже.

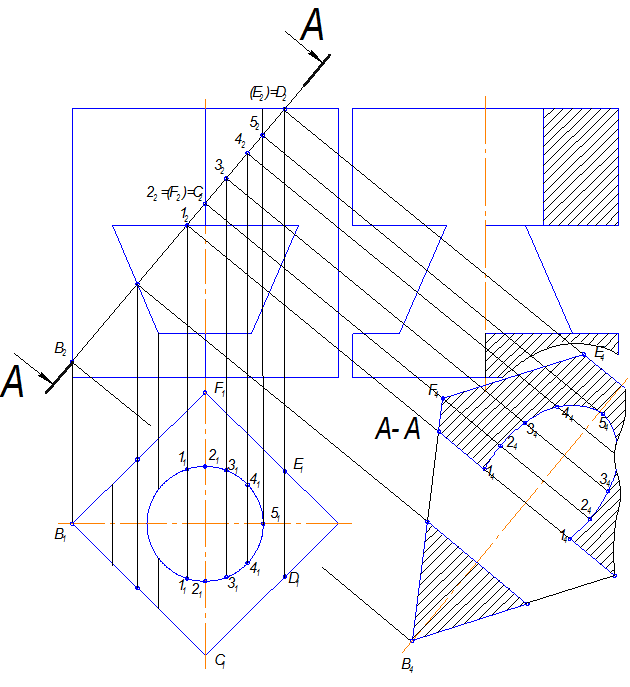
Рис.11.3

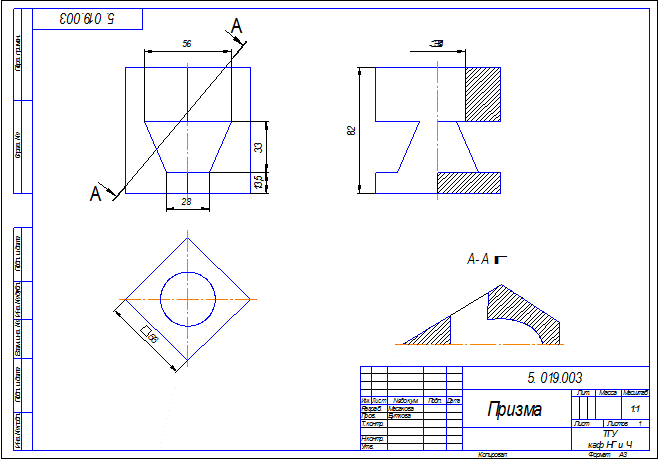
Рис.11.4

Наклонное сечение можно поворачивать. При этом обозначение сопровождается знаком . Также разрешается показать половину фигуры наклонного сечения, если она симметрична. Подобное расположение наклонного сечения показано на рис.13.4. Обозначения точек при построении наклонного сечения можно не ставить.

На рис.11.5 дано наглядное изображение заданной фигуры с сечением плоскостью А-А .

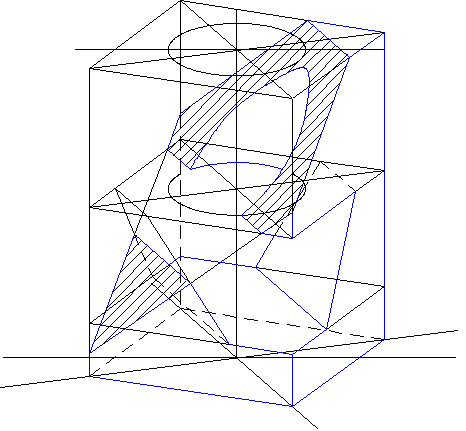
Рис. 11.5

Контрольные вопросы

1. Что называют видом?

2. Как получают изображение предмета на плоскости?

3.Какие названия присвоены видам на основных плоскостях проекций?

4.Что называют главным видом?

5.Что называют дополнительным видом?

6. Что называют местным видом?

7.Что называют разрезом?

8. Какие обозначения и надписи установлены для разрезов?

9. В чем отличие простых разрезов от сложных?

10.Какая соблюдается условность при выполнении ломаных разрезов?

11. Какой разрез называется местным?

12. При каких условиях допускается совмещать половину вида и половину разреза?

13. Что называют сечением?

14. Как располагают сечения на чертежах?

15. Что называют выносным элементом?

16. Как упрощенно показывают на чертеже повторяющиеся элементы?

17. Как условно сокращают на чертеже изображение предметов большой длины?

18. Чем отличаются аксонометрические проекции от ортогональных?

19. Каков принцип образования аксонометрических проекций?

20. Какие установлены виды аксонометрических проекций?

21. Каковы особенности изометрии?

22. Каковы особенности диметрии?

Библиографический список

1. Суворов, С.Г.Машиностроительное черчение в вопросах и ответах: (справочник)/ С.Г.Суворов, Н.С.Суворова.-2-е изд. перераб. и доп. - М.: Машиностроение,1992.-366с.

2. Федоренко В.А. Справочник по машиностроительному черчению/ В.А.Федоренко, А.И.Шошин,- Изд.16-стер.;м Перепеч. с 14-го изд.1981г.-М.: Альянс,2007.-416с.

3.Боголюбов, С.К.Инженерная графика: Учебник для сред. спец. учеб. заведений по спец. техн. профиля/ С.К.Боголюбов.-3-е изд., испр. и доп.-М.: Машиностроение, 2000.-351с.

4.Вышнепольский, И.С.Техническое черчение е. Учеб. для нач. проф. образования/ И.С.Вышнепольский.-4-е изд., перераб. и доп.; Гриф МО.- М.: Высш. шк.: Академия, 2000.-219с.

5. Левицкий, В.С.Машиностроительное черчение и автоматизация выполнения чертежей: учеб. для втузов/В.С.Левицкий.-6-е изд., перераб. и доп.; Гриф МО.-М.: Высш. шк., 2004.-435с.

6. Павлова, А.А. Начертательная геометрия: учеб. для вузов/ А.А. Павлова-2-е изд., перераб. и доп.; Гриф МО.- М.: Владос, 2005.-301с.

7. ГОСТ 2.305-68*. Изображения: виды, разрезы, сечения/Единая система конструкторской документации. - М.: Изд-во стандартов, 1968.

8. ГОСТ 2.307-68. Нанесение размеров и предельных отклонений/Единая система

конструкторской документации. - М.: Изд-во стандартов,1968.

Скачать архив с текстом документа