Задача по Экономико-математическое моделирование
СОДЕРЖАНИЕ: ФЕДЕРАЛЬНОЕ Вариант № . Нефтеперерабатывающий завод производит в месяц 1500000 л алкилата, 1200000 л крекинг - бензина и 1300000 л изопентола. В результате смешения этих компонентов в пропорциях 1:1:1 и 3:1:2 получается бензин сорта А и Б соответственно. Стоимость 1000 л бензина сорта А и Б соответственно равна 90 и 120 усл. ед..ФЕДЕРАЛЬНОЕ Вариант № .
Нефтеперерабатывающий завод производит в месяц 1500000 л алкилата, 1200000 л крекинг - бензина и 1300000 л изопентола. В результате смешения этих компонентов в пропорциях 1:1:1 и 3:1:2 получается бензин сорта А и Б соответственно. Стоимость 1000 л бензина сорта А и Б соответственно равна 90 и 120 усл. ед.. Определить месячный план производства бензина сорта А и Б, приносящий предприятию максимальную прибыль.
Решите задачу графическим и симплекс-методом. Выполните постановку и найдите решение двойственной задачи.
1. Графический метод решения
| Характеристика |
Бензин |
Ограничения |
|
| А |
Б |
||
| Алкилат |
1 |
3 |
1500 |
| Крекинг – бензина |
1 |
1 |
1200 |
| Изопентол |
1 |
2 |
1300 |
| Прибыль (за 1000л) |
90 |
120 |
|
| План |
х1 |
х2 |
|
![]()
х1 + 3х2 1500,
х1 + х2 1200,
х1 + 2х2 1300,
х1 0, х2 0.
Целевая функция:
f = 90х1 + 120х2 max.
Строим прямые
х1 + 3х2 = 1500, 1
х1 + х2 = 1200, 2
х1 +2 х2 = 1300. 3
Строим направляющий вектор q {90, 120}.
Строим прямую, перпендикулярную направляющему вектору и проходящую через область допустимых решений.
Находим оптимальный план:
![]()
![]() х1
+ х2
= 1200, х1
= 1100,
х1
+ х2
= 1200, х1
= 1100,
х1 +2 х2 = 1300. х2 = 100.
Максимальная прибыль допускается при выпуске 1100 бензина А и 100 бензина Б.
Оптимальное значение целевой функции:
f = 90х1 + 120х2 , f = 901100 + 120100 = 111000.
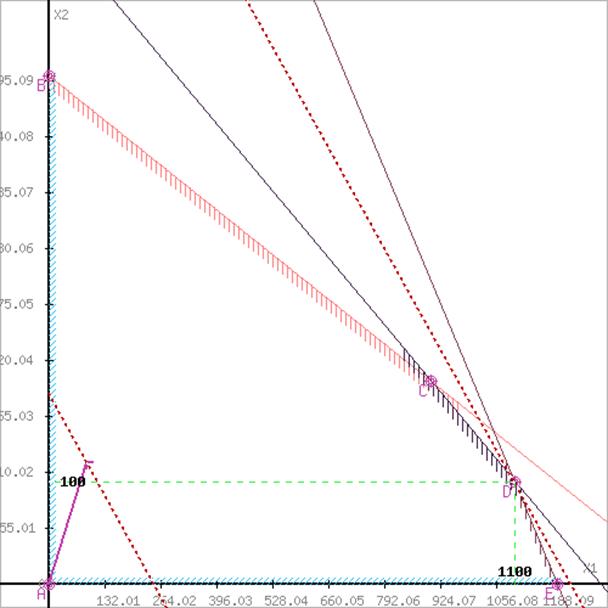 |
2. Симплекс-метод.
| Характеристика |
Бензин |
Ограничения |
|
| А |
Б |
||
| Алкилат |
1 |
3 |
1500 |
| Крекинг – бензина |
1 |
1 |
1200 |
| Изопентол |
1 |
2 |
1300 |
| Прибыль (за 1000л) |
90 |
120 |
|
| План |
х1 |
х2 |
|
Ограничения:![]()
х1 + 3х2 1500,
х1 + х2 1200,
х1 + 2х2 1300,
х1 0, х2 0.
Целевая функция: f = 90х1 + 120х2 max,
Введем дополнительные переменные у1 , у2 , у3 .
![]() 1х1
+ 3х2
+ у1
= 1500,
1х1
+ 3х2
+ у1
= 1500,
1х1 + 1х2 + у2 = 1200,
1х1 + 2х2 + у3 = 1300,
х1 0, х2 0,
у1 0, у2 0, у3 0.
![]() у1
= 1500 – (1х1
+ 3х2
),
у1
= 1500 – (1х1
+ 3х2
),
у2 = 1200 – (1х1 + 1х2 ),
у3 = 1300 – (1х1 + 2х2 ),
х1 0, х2 0,
у1 0, у2 0, у3 0.
f = 0 – (-90х1
– 120х2
) max.
Составим симплекс таблицу:
| Базисные |
Свободные |
x1 |
x2 |
| у1 |
1500 |
1 |
3 |
| у2 |
1200 |
1 |
1 |
| у3 |
1300 |
1 |
2 |
| Индексная строка |
0 |
-90 |
-120 |
Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение. Так как в индексной строке есть отрицательные элементы, то полученное решение не оптимально. Для определения ведущего столбца найдем максимальный по модулю отрицательный элемент в индексной строке (-120). А ведущая строка та, у которой наименьшее положительное отношение свободного члена к соответствующему элементу ведущего столбца.
Пересчитаем таблицу
| Базисные |
Свободные |
x1 |
у1 |
| x2 |
500 |
1/3 |
1/3 |
| у2 |
700 |
2/3 |
-1/3 |
| у3 |
300 |
1 / 3 |
-2/3 |
| Индексная строка |
60000 |
-50 |
40 |
Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение. Так как в индексной строке есть отрицательные элементы, то полученное решение не оптимально. Для определения ведущего столбца найдем максимальный по модулю отрицательный элемент в индексной строке (-50). А ведущая строка та, у которой наименьшее положительное отношение свободного члена к соответствующему элементу ведущего столбца.
Пересчитаем таблицу
| Базисные |
Свободные |
у3 |
у1 |
| X2 |
200 |
-1 |
1 |
| у2 |
100 |
-2 |
1 |
| X1 |
900 |
3 |
-2 |
| Индексная строка |
105000 |
150 |
-60 |
Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение. Так как в индексной строке есть отрицательные элементы, то полученное решение не оптимально. Для определения ведущего столбца найдем максимальный по модулю отрицательный элемент в индексной строке (-60). А ведущая строка та, у которой наименьшее положительное отношение свободного члена к соответствующему элементу ведущего столбца.
Пересчитаем таблицу
| Базисные |
Свободные |
у3 |
у2 |
| x2 |
100 |
1 |
-1 |
| у1 |
100 |
-2 |
1 |
| x1 |
1100 |
-1 |
2 |
| Индексная строка |
111000 |
30 |
60 |
Найдено оптимальное решение.
3. Постановка и решение двойственной задачи.
Основная задача:
![]()
х1 + 3х2 1500,
х1 + х2 1200,
х1 + 2х2 1300,
х1 0, х2 0.
Целевая функция:
f = 90х1 + 120х2 max.
Целевая функция двойственной задачи:
g = 1500y1 + 1200y2 + 1300y3 min.
![]() у1
у1
![]() 1 1 1 у2
1 1 1 у2
3 1 2 у3
![]()
1у1 + 1у2 + 1у3 90,
3у1 + 1у2 + 2у3 120.
Переход от неравенства к равенству:
![]()
х1 + 3х2 + х3 = 1500,
х1 + х2 + х4 = 1200,
х1 + 2х2 + х5 = 1300,
хi 0.
![]()
1у1 + 1у2 + 1у3 - у4 = 90,
3у1 + 1у2 + 2у3 - у5 = 120.
уi 0.
| Осн. |
Осн. |
Доп. |
|||
| х1 |
х2 |
х3 |
х4 |
х5 |
|
| 1100 |
100 |
100 |
0 |
0 |
|
| Двойст. |
0 |
0 |
0 |
60 |
30 |
| у4 |
у5 |
у1 |
у2 |
у3 |
|
| Доп. |
Осн. |
||||