Задачи по статистике 10

СОДЕРЖАНИЕ: Задание1. Распределение работников фирмы по месячной заработной плате характеризуется следующими данными (тыс. руб.): 15, 18, 20, 10, 16, 17, 8, 11, 12, 13, 11, 12, 15, 16, 18, 20, 19, 18, 16, 17, 18, 19, 25, 28, 22, 18, 16, 10, 18, 19, 11, 12, 13, 15, 16, 17, 18, 20, 17, 18, 19, 20, 8, 8, 10, 12, 13, 28, 28, 25, 18, 22.

Задание1. Распределение работников фирмы по месячной заработной плате характеризуется следующими данными (тыс. руб.): 15, 18, 20, 10, 16, 17, 8, 11, 12, 13, 11, 12, 15, 16, 18, 20, 19, 18, 16, 17, 18, 19, 25, 28, 22, 18, 16, 10, 18, 19, 11, 12, 13, 15, 16, 17, 18, 20, 17, 18, 19, 20, 8, 8, 10, 12, 13, 28, 28, 25, 18, 22.

Для анализа распределения работников фирмы по заработной плате требуется:

1. Построить интервальный ряд распределения, выделив 5 групп.

2. Дать графическое изображение ряда.

3. Исчислить показатели центра распределения (мода, медиана, средняя), показатели вариации. Сформулировать вывод.

Решение. Определим сначала размер интервала:

Построим таблицу:

*Группы по заработной плате (* )	*Число работников (* )
От 8 до 12	9
От 12 до 16	10
От 16 до 20	22
От 20 до 24	6
От 24 и более	5
Итого	52

Построим графическое изображение ряда:

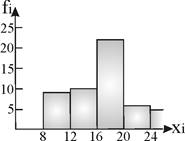Вычислим теперь показатели центра распределения. Начнем с вычисления моды. Модальный интервал в данном случае будет от 16 до 20. Таким образом, мода будет равна:

Рассмотрим следующую характеристику-медиану. Номер медианы будет равен Медиальный интервал, также как и в случае модального интервала, будет от 16 до 20. Таким образом, медиана будет равна:

Для определения средней к нашей таблице добавим еще один столбец, в котором будем записывать конкретные значения варианты:

*Группы по заработной плате (* )	*Число работников (* )	*Варианта*
От 8 до 12	9	10
От 12 до 16	10	14
От 16 до 20	22	18
От 20 до 24	6	22
От 24 и более	5	26
Итого	52

Тогда среднеарифметическая взвешенная будет равна:

Мы видим, что , следовательно, можно сделать вывод, что данное распределение ассиметричное. И последняя характеристика - показатель вариации. Размах вариации Дисперсия будет равна

Следовательно, среднеквадратичное отклонение Тогда коэффициент вариации . Таким образом, из всех проделанных вычислении можно свидетельствовать об однородности совокупности заработной платы и устойчивой средней.

Задание 2. Распределение численности мужчин и женщин по возрастным группам на 1 января 2008 года в Томской области характеризуется следующими данными:

*Группы по возрасту (лет)*	*Мужчины*	*Женщины*
0-4	29050	27556
5-9	24661	23852
10-14	23985	22684
15-19	36615	36947
20-24	59443	59809
25-29	51120	52249
30-34	38488	38733
35-39	33372	34413
40-44	31062	33580
45-49	39196	44196
50-54	36398	43572
55-59	29325	37682
60-64	13932	18625
65-69	15286	23957
70 лет и старше	22057	53140
Итого	483990	550995

Определить:

1. Относительные величины структуры и координации;

2. Удельный вес лиц моложе трудоспособного возраста, в трудоспособном возрасте и старше трудоспособного возраста;

3. Коэффициенты демографической нагрузки детьми, пожилыми о общий;

4. Оценить уровень старения населения, используя шкалу польского демографа Э. Россета и таблицу Зунберга.

Решение.

Для нахождения относительных величин структуры и координации необходимо добавить дополнительные столбцы:

*Группы по возрасту (лет)*	*Мужчины*	*Женщины*	*Удельный вес, мужчины,%*	*Удельный вес, женщины,%*	*ОВК*
0-4	29050	27556	6,0	5,0	948
5-9	24661	23852	5,1	4,3	967
10-14	23985	22684	5,0	4,1	945
15-19	36615	36947	7,6	6,7	1009
20-24	59443	59809	12,3	10,9	1006
25-29	51120	52249	10,6	9,5	1022
30-34	38488	38733	8,0	7,0	1006
35-39	33372	34413	6,9	6,2	1031
40-44	31062	33580	6,4	6,1	1081
45-49	39196	44196	8,1	8,0	1127
50-54	36398	43572	7,5	7,9	1197
55-59	29325	37682	6,1	6,8	1284
60-64	13932	18625	2,9	3,4	1336
65-69	15286	23957	3,2	4,3	1567
70 лет и старше	22057	53140	4,6	9,6	2409,21
Итого	483990	550995	100,3	99,8	-

Удельный вес лиц моложе трудоспособного возраста:

Удельный вес лиц в трудоспособном возрасте:

Удельный вес лиц старше трудоспособного возраста:

Коэффициент демографической нагрузки детьми:

Коэффициент демографической нагрузки пожилыми:

Общий коэффициент демографической нагрузки:

Наконец, определим уровень старения населения. Рассчитаем его стачала с помощью таблицы Зунберга. Приведем более удобный вид нашей таблицы:

*Группы по возрасту (лет)*	*Мужчины*	*Женщины*
0-14	16,05	13,46
15-49	59,77	54,43
50 и старше	24,17	32,12
Итого	99,99	100,1

Из таблицы видно, что и для мужчин, и для женщин уровень старения населения регрессивный.

С другой стороны, используя шкалу Россета:

-для мужчин

-для женщин

Откуда можно сделать вывод, что для женщин характерна демографическая старость, в то время как для мужчин характерно собственно старение, хотя и характеристика близка к преддверию старости.

Задание3. Оцените тесноту связи между онкологическим заболеваниями и работой со свинцом, используя коэффициенты ассоциации и контингенции:

*Работа со свинцом*	*Обследовано рабочих*		*Всего*
*Работа со свинцом*	*Онкологические больные*	*Здоровые*	*Всего*
Да	14	4	18
Нет	31	41	72
Итого	45	45	90

Решение.

Коэффициент ассоциации:

Коэффициент контингенции:

Так как , то онкологические заболевания действительно зависят от того, работает человек со свинцом или нет.

Задание4. Для определения средней суммы вклада в коммерческом банке, имеющем 3000 вкладчиков, проведено выборочное обследование (бесповторный отбор) 150 вкладов, которое дало следующие результаты:

*Сумма вклада, тыс. руб.*	До 30	От 30 до 40	От 40 до 50	От 50 до 60	От 60 и более
*Число вкладов*	5	20	80	30	15

Найти доверительные границы среднего размера в сберегательном банке для всех вкладов с вероятностью 0,997.

Решение.

Для данной задачи коэффициент доверия t =3 . Чтобы найти доверительные границы среднего размера в сберегательном банке с данной вероятностью, необходимо найти предельную ошибку:

Для этого нужно найти ошибку репрезентативности:

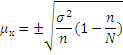
Следовательно, надо найти по формуле:

Тогда находим среднее:

Следовательно:

Отсюда

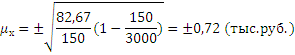
Тогда

Окончательно получаем:

Задание5. По Томской области имеются следующие данные о численности населения и его миграции:

*№ строки*	*Показатели*	*1998 год*	*1999 год*	*2004 год*	*2007 год*
1	Среднегодовая численность населения	1072,5	1069,7	1038,7	1034,05
2	Прибыло	24,7	23,5	16,5	20,0
3	Выбыло	23,5	24,2	18,1	17,3

Определить абсолютные и относительные показатели миграции населения Томской области. Проанализировать динамику и сделать выводы.

Решение.

Все абсолютные и относительные показатели занесем в таблицу:

*№ строки*	*Показатели*	*1998 год*	*1999 год*	*2004 год*	*2007 год*
1	Среднегодовая численность населения	1072,5	1069,7	1038,7	1034,05
2	Прибыло	24,7	23,5	16,5	20,0
3	Выбыло	23,5	24,2	18,1	17,3
4	Абсолютный миграционный прирост	1,2	-0,7	-1,6	2,7
5	Объем миграции	48,2	47,7	34,6	37,3
6	Коэффициент прибытия,‰	23,03	21,97	15,89	19,34
7	Коэффициент выбытия,‰	21,91	22,62	17,43	16,73
8	Коэффициент миграционного прироста,‰	1,12	-0,65	-1,54	2,61
9	Коэффициент интенсивности миграционного оборота,‰	44,94	44,59	33,31	36,07
10	Коэффициент эффективности миграции	0,0249	-0,0147	-0,0462	0,0724

Задание6. Имеются следующие данные о реализации молочных продуктов на одном из рынков города:

*Наименование товара*	*Товарооборот (тыс. руб.)*		*Изменение объема реализации товаров в сентябре (%)*
*Наименование товара*	*Август*	*Сентябрь*	*Изменение объема реализации товаров в сентябре (%)*
Молоко	197	223	+10
Сметана	245	240	Без изменения
Творог	383	427	+5
Итого	825	890

Рассчитайте индивидуальные и сводные индексы товарооборота, физического объема товарооборота и цен. Абсолютный прирост товарооборота за счет отдельных факторов. Как изменилась покупательная способность денежной единицы? Сделать выводы.

Решение.

Добавим к нашей таблице еще один столбец, который будет отображать индивидуальный индекс физического объема:

*Наименование товара*	*Товарооборот (тыс. руб.)*		*Изменение объема реализации товаров в сентябре (%)*	*(%)*
*Наименование товара*	*Август*	*Сентябрь*	*Изменение объема реализации товаров в сентябре (%)*	*(%)*
Молоко	197	223	+10	110
Сметана	245	240	Без изменения	100
Творог	383	427	+5	95
Итого	825	890