Расчет надежности электроснабжения подстанции Южная
СОДЕРЖАНИЕ: МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра электрооборудованияМИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО
ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра электрооборудования
КУРСОВАЯ РАБОТА
по курсу: «Надежность электроснабжения»
на тему: «Расчет надежности электроснабжения подстанции Южная»
Выполнил студент
гр. ЭО – 95 Васин А.В.
___________________
«__» _________ 1999
Принял доцент, к.т.н.,
Челядин В. Л.
___________________
___________________
«__» _________ 1999
Липецк 1999
ОГЛАВЛЕНИЕ
ЗАДАНИЕ......................................................................................... 3
ВВЕДЕНИЕ...................................................................................... 5
1 РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ ЭЛЕМЕНТОВ...... 6
1.1. Модель отказов и восстановления силового
трансформатора........................................................................... 6
1.2 Модель отказов автоматического выключателя................... 10
1.3. Модель отказов воздушной линии электропередач........... 13
1.4. Модель отказов и восстановления для разъединителей...... 17
1.5. . Модель отказов и восстановления для отделителей и
короткозамыкателей.................................................................... 18
1.6. Модель отказов и восстановления для шин......................... 19
2. РАСЧЕТ НАДЕЖНОСТИ СХЕМЫ ЭЛЕКТРОСНАЖЕНИЯ... 21
2.1. Расчет последовательных соединений.................................. 21
2.2. Учет резервирования............................................................. 27
ЗАКЛЮЧЕНИЕ................................................................................ 30
БИБЛИОГРАФИЧЕСКИЙ СПИСОК ИСПОЛЬЗОВАННЫХ
ИСТОЧНИКОВ................................................................................ 31
ЗАДАНИЕ
1. На основании статистических данных определить показатели надежности отдельных элементов схемы электроснабжения подстанции Южная.
2. Составить структурно-логическую схему, основанную на анализе функционирования системы, учете резервирования, восстановлений, контроля исправности элементов.
3. Выбрать метод расчета надежности с учетом принятых моделей и описаний процессов функционирования и восстановления.
4. Получить в общем виде математическую модель, связывающую показатели надежности с характеристиками элементов.
5. Выполнить расчет и анализ полученных результатов.
Исходные данные приведены на рис.1 и в табл. 1.
Таблица 1
Оборудование подстанции учитываемое при расчете надежности
| ЛЭП1 |
АС185 |
| ЛЭП2 |
АС185 |
| QS1 |
РНД31-110У/1000 |
| QS2 |
РНД31-110У/1000 |
| QR1 |
ОД110т/630 |
| QR2 |
ОД110т/630 |
| QK1 |
КЗ-110т |
| QK2 |
КЗ-110т |
| Т1 |
ТДТН- 40000/110 |
| Т2 |
ТДТН- 40000/110 |
|
QF1 |
ВМП 10э |
| QF2 |
ВМП 10э |
| QF4 |
ВМП 10э |
| QF5 |
ВМП 10э |
| QF3 |
ВМП 10к |
| QF3 |
ВМП 10к |
| Шины 10 кВ |
|
| Шины 6 кВ |
ВВЕДЕНИЕ
Проблема обоснования целесообразного уровня надежности систем электроснабжения на современном этапе развития имеет большое значение. Аварийные и внезапные перерывы электроснабжения потребителей вызывают большой народнохозяйственный ущерб, обусловленный поломкой оборудования, порчей сырья и материалов, затратами на ремонты, недовыпуском продукции, простоями технологического оборудования и рабочей силы, а также издержками связанными с другими факторами.
Сегодня методы анализа надежности используются уже во многих отраслях техники. Однако проблема надежности в ее количественной постановке при проектировании и эксплуатации систем электроснабжения необыкновенно сложна. Так для рассмотрения вопросов надежности, при эксплуатации систем электроснабжения необходимо учесть как современные достижения современной теории надежности, так и специфику функционирования систем силового типа, подверженных в значительной степени влиянию неблагоприятных воздействий внешней среды и непосредственно связанных с электрической системой.
Целью данной работы является попытка рассмотрения надежности функционирования оборудования подстанции, и связанная с этим надежность бесперебойного обеспечения потребителей электроэнергией.
1. РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ ЭЛЕМЕНТОВ
1.1. Модель отказов и восстановления силового трансформатора
Рассмотрим трансформатор как элемент, условно состоящий из двух последовательно соединенных элементов, в одном из которых могут появляться внезапные отказы, а в другом - постепенные. Внезапные отказы появляются вследствие резкого, внезапного изменения основных параметров под воздействием одного или нескольких случайных факторов внешней среды либо вследствие ошибок обслуживающего персонала. При постепенных отказах наблюдается плавное, постепенное изменение параметра элементов в результате износа отдельных частей или всего элемента в целом.
Вероятность безотказной работы представим произведением вероятностей
Ртр (t)=Рв (t)*Ри (t), (1.1)
где Рв (t) и Ри (t) — соответственно вероятности безотказной работы условных элементов, соответствующих внезапному и постепенному отказу в следствии износа.
В теории надежности в качестве основного распределения времени безотказной работы при внезапных отказах принимается показательное распределение:
![]() (1.2)
(1.2)
Постепенные отказы трансформатора происходит в основном по причине износа изоляции . Износ можно описать законом распределения Вейбулла-Гнеденко
![]() (1.3)
(1.3)
где t0 — порог чувствительности, то есть элемент гарантировано не откажет , в интервале времени от 0 до t0 может быть равно нулю. Тогда окончательно имеем:
![]() Pтр
(t) = e-
l
t
e-ct
. (1.4)
Pтр
(t) = e-
l
t
e-ct
. (1.4)
Причинами внезапных отказов трансформатора являются повреждения вводов трансформатора вследствие перекрытия контактных соединений, утечка масла. Причинами постепенных отказов в свою очередь будут нарушения изоляции обмоток вследствие возникновения внешних и внутренних перенапряжений, сквозных токов коротких замыканий и дефектов изготовления. На основании принятых критериев выделим два статистических ряда для внезапных и постепенных отказов табл.2.
Таблица 2
Статистический ряд внезапных и постепенных отказов силового трансформатора
| Y, ч |
Y, ч |
Y, ч |
X, ч |
X, ч |
X, ч |
| 61039 |
57546 |
53529 |
43774 |
45022 |
45850 |
| 59612 |
55392 |
51355 |
41283 |
42078 |
42906 |
| 57981 |
53986 |
60205 |
38793 |
39628 |
40455 |
| 56107 |
52062 |
58217 |
36302 |
36728 |
37554 |
| 54349 |
60483 |
56438 |
44608 |
45436 |
46264 |
| 52573 |
58564 |
55216 |
41664 |
42492 |
43320 |
| 60761 |
56854 |
52914 |
39215 |
40041 |
40869 |
| 58783 |
55739 |
50785 |
36581 |
37141 |
37967 |
| 54733 |
38380 |
||||
| Yср |
D t |
Т |
l |
||
| 56209 |
1827 |
40974 |
2,44057E-05 |
Параметр показательного закона l находим по формуле:
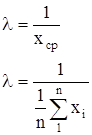 (1.4)
(1.4)
где хср — среднеее значение наработок на отказ.
Среднее время безотказной работы определим по формуле
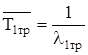 (1.5)
(1.5)
Оценим параметры распределения Вейбулла-Гнеденко. Для этого вычислим среднеее значение наработки на отказ
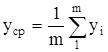 (1.6)
(1.6)
Разобьем выборку y на интервалы, которые выберем по формуле
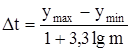 (1.7)
(1.7)
Подсчитаем сколько отказов попало в каждый из полученных интервалов
Таблица 3
| интервалы |
1 |
2 |
3 |
4 |
5 |
6 |
| мин |
50785 |
52612 |
54439 |
56265 |
58092 |
59919 |
| макс |
52612 |
54439 |
56265 |
58092 |
59919 |
61746 |
| 1 |
52573 |
54349 |
57981 |
56107 |
59612 |
61039 |
| 2 |
52062 |
53986 |
57546 |
55392 |
58783 |
60761 |
| 3 |
51355 |
53529 |
56854 |
55739 |
58564 |
60483 |
| 4 |
50785 |
52914 |
56438 |
55261 |
58217 |
60205 |
| Yicp |
51694 |
53695 |
57205 |
55444 |
58794 |
60622 |
| pi |
0,16 |
0,16 |
0,16 |
0,2 |
0,16 |
0,16 |
| D |
s |
n |
1/ a |
C |
T |
l |
| 8734345 |
2955 |
0,052578 |
0,045 |
1,63E-106 |
56209 |
1,779E-05 |
Отностительную частоту событий определяем по формуле
pi = mi /m. (1.8)
Определим среднее значение для каждого интервала
![]() (1.9)
(1.9)
Вычислим значение дисперсии D по формуле:
![]() (1.10)
(1.10)
Определим среднеквадратичное отклонение:
![]() . (1.11)
. (1.11)
Вычислим коэффициент вариации по формуле:
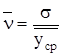 . (1.12)
. (1.12)
По номограмме находим значение параметра формы 1/a=0,31.По найденным значениям вычислим параметр масштаба С распределения Вейбула-Гниденко :
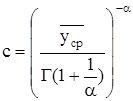 (1.13)
(1.13)
Г(1,0351)=0,987
Среднее время безотказной работы для распределения Вейбула-Гниденко определим по формуле
![]() ; (1.14)
; (1.14)
l2тр =1/Т2тр =0,00002 (1.15)
Интенсивность восстановления определим по данным статистического ряда представленном в таблице 4
Таблица 4
Статистический ряд времени восстановления внезапных и
постепенных отказов силового трансформатора
| восстановление |
|||
| 15,8 |
18,7 |
22,4 |
26,1 |
| 18,2 |
21,7 |
25,4 |
20,5 |
| 21,2 |
24,7 |
17,6 |
23,6 |
| 24,2 |
17,1 |
20,1 |
26,5 |
| 16,4 |
19,5 |
22,9 |
27,2 |
| Т= 21,49 |
m = 0,0465333 |
||
Интенсивность восстановления определим по формуле :
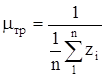 (1.16)
(1.16)
Вероятность восстановления силовых трансформаторов определим по формуле
Рвос.тр =1-е- m тр. (1.17)
Результаты расчетов по формулам (1.1)-(1.17) представлены в табл.2,3,4.
1.2. Модель отказов автоматического выключателя
Рассмотрим масляный выключатель как элемент состоящий из двух элементов, в одном из которых может появиться внезапный отказ, а в другом постепенный. Вероятность безотказной работы представлена формулой
Рвк (t)=Рв (t)*Ри (t)
где Рв (t) и Ри (t) — соответственно вероятности безотказной работы условных элементов соответствующих внезапному и постепенному отказу в следствии износа.
Постепенные отказы выключателя происходят в следствии износа дугогасительных камер и контактов. Причинами внезапного отказа являются: несрабатывание приводов, механические повреждения, перекрытие изоляции при внешних и внутренних перенапряжениях. На основании принятых критериев сформируем два статистических ряда представленных в таблице 5.
Таблица 5
Статистический ряд внезапных и постепенных отказов
вводного масляного выключателя
| X, ч |
X, ч |
X, ч |
Y, ч |
Y, ч |
Y, ч |
| 7842 |
8557 |
8554 |
8961 |
11568 |
7568 |
| 8749 |
10412 |
10715 |
10052 |
14008 |
11434 |
| 10436 |
11238 |
11102 |
8499 |
14699 |
9918 |
| 12650 |
11476 |
12317 |
10955 |
11463 |
8079 |
| 15540 |
20379 |
15451 |
10662 |
11650 |
14350 |
| 9452 |
11510 |
13480 |
9462 |
9734 |
17044 |
| 6358 |
6693 |
7752 |
17465 |
16484 |
13927 |
| 7075 |
7683 |
6958 |
16155 |
17535 |
16736 |
| 10349 |
|||||
| Т |
l |
Yср |
l0 |
||
| 10516 |
9,5E-05 |
12350 |
8,1E-05 |
Согласно теории надежности внезапные отказы имеют показательный закон распределения наработки на отказ
Параметр показательного закона распределения опеределим по формуле (1.4)
где хср — среднеее значение наработок на отказ.
Среднее время безотказной работы определим по формуле (1.5)
Постепенные отказы выключателя имеют следующий закон распределения
![]() (1.17)
(1.17)
где l0 – это интенсивность срабатывания выключателя, которая определяется по данным статистического ряда
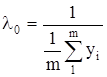 ;
;
R— допустимое число отключений.
Предпологая, что коммутирующий ток распределен по нормальному закону между максимальным и минимальным значением. Определим расход рr :
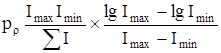 ;
;
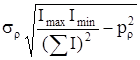
Imax и Imin — максимальный и минимальный коммутируемый ток;
SI— произведение номинального тока отключения на гарантированое число отключений.
Допустимое число отключений определим по формуле
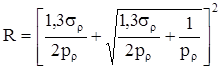
Среднее время безотказной работы при постепенных отказах
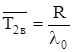
Интенсивность восстановления определим по данным из таблицы 6 и формуле (1.16)
Таблица 6
Статистический ряд времени восстановления внезапных
и постепенных отказов вводного масляного выключателя
| восстановление |
|||
| 16,6 |
20,0 |
22,8 |
19,8 |
| 25,6 |
25,9 |
19,6 |
21,4 |
| 18,0 |
24,6 |
19,4 |
21,2 |
| 18,4 |
22,0 |
17,1 |
18,6 |
| 21,3 |
21,1 |
17,5 |
17,5 |
| Т= 20,4196 |
m = 0,04897 |
||
Таблица 7.
Результаты расчетов
| Imax |
Imin |
n |
Iоткл |
| 7,5 |
5 |
20 |
20 |
| SI |
рr |
sr |
k |
| 400 |
0,0066 |
0,01381 |
121 |
Интенсивность восстановления определим по формуле :
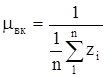 ;
;
Вероятность восстановления масляного выключателя ВКЭ поределяется по формуле
Рвос.вк = 1-е- m .
Результаты расчетов по приведенным выше формулам сведены в табл.5,6,7.
Аналогично проведем расчеты для секционного маслянного выключателя. Исходные данные и результаты расчетов сведены в табл. 8,9,10.
Таблица 8
Статистический ряд внезапных и постепенных отказов
секционного масляного выключателя
| X, ч |
X, ч |
X, ч |
Y, ч |
Y, ч |
Y, ч |
| 8341,45 |
9107,29 |
9104 |
9637 |
12466 |
8128 |
| 9313,07 |
11096,7 |
11422,3 |
10820 |
15119 |
12321 |
| 11123 |
11982,9 |
11837 |
9137 |
15871 |
10675 |
| 13500 |
12238,5 |
13142 |
11801 |
12352 |
8682 |
| 16607,9 |
21820,4 |
16512,2 |
11483 |
12556 |
15490 |
| 10066,5 |
12275,9 |
14392,1 |
10180 |
10475 |
18424 |
| 6752,77 |
7111,97 |
8245,21 |
18883 |
17814 |
15031 |
| 7520,51 |
8170,86 |
7394,87 |
17455 |
18960 |
18088 |
| 11143 |
|||||
| Т |
l |
Yср |
l0 |
||
| 11212 |
8,9E-05 |
13320 |
7,5E-05 |
Таблица 9
Статистический ряд времени восстановления внезапных
и постепенных отказов секционного масляного выключателя
| восстановление |
|||
| 16,5 |
19,9 |
22,6 |
19,7 |
| 25,5 |
25,8 |
19,5 |
21,2 |
| 17,9 |
24,5 |
19,3 |
21,0 |
| 18,3 |
21,8 |
17,0 |
18,5 |
| 21,1 |
20,9 |
17,4 |
17,4 |
| Т= 20,2969 |
m = 0,04927 |
||
Таблица 10.
Результаты расчетов
| Imax |
Imin |
n |
Iоткл |
| 5,5 |
4 |
20 |
20 |
| SI |
рr |
sr |
k |
| 400 |
0,00507 |
0,01057 |
162 |
1.3. Модель отказов воздушной линии электропередач
ЛЭП рассмотрим как элемент условно состоящий из двух последовательно соединенных элементов. В одном из которых может появиться внезапный отказ, а в другом постепенный. Вероятность безотказной работы представим как произведение вероятности двух независимых событий соединенных последовательно отностительно надежности.
РЛЭП (t)=Рв (t)*Ри (t).
Дальнейший расчет проведем как и для трансформатора. Статистические данные приведенные в таблице 11 приведены к единичной длине 1 км, как для внезапных и постепенных отказов.
Таблица 11
Статистический ряд внезапных и постепенных отказов для ЛЭП
| X, г |
X, г |
X, г |
Y, г |
Y, г |
Y, г |
| 174,11 |
203,04 |
179,13 |
309,12 |
326,04 |
343,86 |
| 180,83 |
41213 |
187,67 |
316,75 |
334,17 |
351,59 |
| 189,38 |
208,17 |
194,54 |
324,5 |
341,94 |
313,62 |
| 201,33 |
177,41 |
211,58 |
332,25 |
349,68 |
321,37 |
| 206,46 |
185,96 |
196,21 |
340,02 |
312,08 |
329,12 |
| 175,72 |
192,79 |
213,29 |
347,75 |
319,82 |
338,01 |
| 184,25 |
204,75 |
197,92 |
310,54 |
327,58 |
345,78 |
| 191,08 |
209,88 |
215,67 |
318,29 |
336,09 |
363,25 |
| Т |
l |
Yср |
D t |
||
| 1904 |
0,00052523 |
331 |
10 |
В теории надежности в качестве основного распределения времени безотказной работы при внезапных отказах ЛЭП принимается показательное распределение:
![]()
Постепенные отказы ЛЭП происходят в основном по причине износа изоляции. Износ можно описать законом распределения Вейбула-Гниденко.
![]()
где t0 — порог чувствительности, то есть элемент гарантировано не откажет, в интервале времени от 0 до t0 может быть равно нулю. Тогда окончательно имеем:
![]() PЛЭП
(t) = e-
l
t
e-ct
=.
PЛЭП
(t) = e-
l
t
e-ct
=.
Параметр показательного закона l находим по формуле:
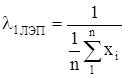
где хср — среднеее значение наработок на отказ.
Среднее время безотказной работы определим по формуле
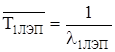
Оценим параметры распределения Вейбула-Гниденко. Для этого вычислим среднеее значение наработки на отказ
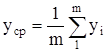
Разобьем выборку y на интервалы, которые выберем по формуле
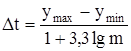
Подсчитаем сколько отказов попало в каждый из полученных интервалов
Таблица 12
| интервалы |
1 |
2 |
3 |
4 |
5 |
6 |
| мин |
309,12 |
318,86 |
328,61 |
338,35 |
348,10 |
357,84 |
| макс |
319 |
329 |
338 |
348 |
358 |
368 |
| 1 |
309,12 |
316,75 |
324,5 |
332,25 |
340,02 |
347,75 |
| 2 |
310,54 |
318,29 |
326,04 |
334,17 |
341,94 |
349,68 |
| 3 |
312,08 |
319,82 |
327,58 |
336,09 |
343,86 |
351,59 |
| 4 |
313,62 |
321,37 |
329,12 |
338,01 |
345,78 |
363,25 |
| Yicp |
311 |
319 |
327 |
335 |
343 |
353 |
| pi |
0,1666666 |
0,1666666 |
0,1666666 |
0,16667 |
0,16667 |
0,16667 |
| D |
s |
n |
1/a |
C |
T |
l |
| 199 |
14 |
0,0425237 |
0,035 |
5,7E-73 |
331 |
0,00302 |
Отностительную частоту событий определяем по формуле
pi = mi /m.
Определим среднее значение для каждого интервала
![]()
Вычислим значение дисперсии D по формуле:
![]()
Определим среднеквадратичное отклонение:
![]() .
.
Вычислим коэффициент вариации по формуле:
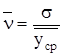 .
.
По номограмме находим значение параметра формы 1/a=0,36. По найденным значениям вычислим параметр масштаба С распределения Вейбула-Гниденко :
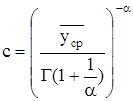
Г(1,36)=0,8902
Среднее время безотказной работы для распределения Вейбула-Гниденко определим по формуле
![]() ;
;
l2ЛЭП =1/Т2ЛЭП
В таблице 13 представлен статистический ряд восстановления отказов ЛЭП.
Интенсивность восстановления определим по формуле (1.16)
Вероятность восстановления ЛЭП определяется по формуле
Рвос.ЛЭП =1-е- m .
Таблица 13
Статистический ряд восстановления внезапных и постепенных отказов ЛЭП
| восстановление |
|||
| 7,1 |
9,2 |
11,3 |
13,4 |
| 8,9 |
10,9 |
13 |
8,6 |
| 10,7 |
12,7 |
8,1 |
10,3 |
| 12,3 |
4,8 |
9,9 |
12,1 |
| 4,5 |
9,6 |
11,7 |
18,8 |
| Т= |
10,395 |
m = |
0,0962 |
Результаты расчетов по приведенным выше формулам сведены в табл.11,12,13.
1.4. Модель отказов и восстановления для разъединителей
Представим разъединитель как элемент состоящий из одного элемента с внезапным отказом, с показательным законом распределения наработки на отказ (1,1). Статистический ряд представлен в таблице 14, 15 наработок на отказ и времени восстановления.
Параметр показательного закона l находим по формуле:
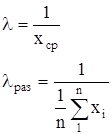
где хср — среднеее значение наработок на отказ.
Среднее время безотказной работы определим по формуле
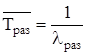
Таблица 14
Статистический ряд внезапных отказов разъединителей
| X, г |
X, г |
X, г |
X, г |
| 6,64 |
7,40 |
6,68 |
7,13 |
| 7,06 |
7,17 |
7,44 |
7,06 |
| 6,86 |
7,12 |
7,20 |
7,22 |
| 7,20 |
6,98 |
6,83 |
7,11 |
| 6,79 |
6,83 |
7,24 |
7,48 |
| Т= 7 |
l= 0,14143 |
||
Интенсивность восстановления определим по формуле (1.16) ![]()
Вероятность восстановления разъединителей определяется:
Рвос.раз =1-е- m .
Таблица 15
Статистический ряд времени восстановления разъединителей
| восстановление |
|||
| 8,3 |
6 |
6,2 |
7 |
| 7,5 |
8 |
8,3 |
7,2 |
| 9,1 |
9,2 |
10,9 |
9 |
| 6,8 |
10,4 |
9,4 |
8,1 |
| 10,1 |
7,1 |
8,5 |
6,1 |
| Т= 8,16 |
m = 0,12255 |
||
Результаты расчетов по приведенным выше формулам сведены в табл.14,15.
1.6. Модель отказов и восстановления для отделителей и короткозамыкателей
Для отделителей и короткозамыкателей составим модель аналогичную разъединителям и проведем подобный расчет. Исходные данные и результаты расчета сведем в таблицу 16,17,18,19.
Таблица 16
Статистический ряд внезапных отказов отделителей
| X, ч |
X, ч |
X, ч |
X, ч |
| 31377 |
35695 |
31623 |
34179 |
| 33786 |
34416 |
35974 |
33762 |
| 32653 |
34130 |
34558 |
34679 |
| 34579 |
33325 |
32455 |
34091 |
| 32231 |
32471 |
34825 |
36149 |
| Т= 33848 |
l= 3E-05 |
||
Таблица 17
Статистический ряд времени восстановления отделителей
| восстановление |
|||
| 8,1 |
5,9 |
6,1 |
6,9 |
| 7,4 |
7,8 |
8,1 |
7,1 |
| 8,9 |
9,0 |
10,6 |
8,8 |
| 6,7 |
10,2 |
9,2 |
7,9 |
| 9,9 |
7,0 |
8,3 |
6,0 |
| Т= 7,98933 |
m = 0,12517 |
||
Таблица 18
Статистический ряд внезапных отказов короткозамыкателей
| X, ч |
X, ч |
X, ч |
X, ч |
| 32430 |
36893 |
32685 |
35326 |
| 34920 |
35570 |
37181 |
34895 |
| 33749 |
35275 |
35718 |
35842 |
| 35739 |
34443 |
33544 |
35235 |
| 33312 |
33560 |
35993 |
37362 |
| Т= |
34984 |
l= |
2,9E-05 |
Таблица 19
Статистический ряд времени восстановления короткозамыкателей
| восстановление |
|||
| 8,3 |
6 |
6,2 |
7 |
| 7,5 |
8 |
8,3 |
7,2 |
| 9,1 |
9,2 |
10,9 |
9 |
| 6,8 |
10,4 |
9,4 |
8,1 |
| 10,1 |
7,1 |
8,5 |
6,1 |
| Т= 8,16 |
m = 0,12255 |
||
1.6. Модель отказов и восстановления для шин
Рассматриваем два типа шин: питающие шины, идущие от трансформатора к вводному выключателю; секции шины. Так как шины голые то для них применим показательный закон распределения внезапных отказов. Причиной внезапных отказов является воздействие токов короткого замыкания. Расчет произведем аналогично результаты расчетев сведем в таблицу 20,21,22,23
Таблица 20
Статистический ряд внезапных отказов питающих шин
| X, ч |
X, ч |
X, ч |
X, ч |
| 760215 |
856936 |
768768 |
867865 |
| 1001326 |
870594 |
1001022 |
874998 |
| 794916 |
905950 |
964405 |
814378 |
| 969966 |
956631 |
840253 |
903270 |
| 888089 |
806707 |
894381 |
823804 |
| Т= |
878224 |
l= |
1,14E-06 |
Таблица 21
Статистический ряд времени восстановления питающих шин
| восстановление |
|||
| 2,1 |
2,9 |
2,3 |
3,5 |
| 3,7 |
3,8 |
3,8 |
3,9 |
| 3,0 |
4,3 |
3,0 |
3,7 |
| 4,4 |
3,9 |
4,7 |
2,4 |
| 3,3 |
3,6 |
3,1 |
4,2 |
| Т= 3,48353 |
m = 0,28707 |
||
Таблица 22
Статистический ряд внезапных отказов секций шин
| X, ч |
X, ч |
X, ч |
X, ч |
| 760215 |
856936 |
768768 |
867865 |
| 1001326 |
870594 |
1001022 |
874998 |
| 794916 |
905950 |
964405 |
814378 |
| 969966 |
956631 |
840253 |
903270 |
| 888089 |
806707 |
894381 |
823804 |
| Т= |
878224 |
l= |
1,1E-06 |
Таблица 23
Статистический ряд времени восстановления секций шин
| восстановление |
|||
| 2,0 |
2,7 |
2,2 |
3,3 |
| 3,5 |
3,6 |
3,6 |
3,7 |
| 2,8 |
4,2 |
2,8 |
3,5 |
| 4,3 |
3,7 |
4,5 |
2,3 |
| 3,1 |
3,4 |
2,9 |
4,1 |
| Т= 3,33011 |
m = 0,30029 |
||
2. РАСЧЕТ НАДЕЖНОСТИ СХЕМЫ ЭЛЕКТРОСНАЖЕНИЯ
2.1. Расчет последовательных соединений
Анализ системы последовательно соединенных, восстанавливаемых элементов будем проводить с учетом двух условий: первое при отказе одного элемента интенсивности отказа оставшихся в работе элементов не изменяются; второе восстановление не ограничено, т.е. любой отказавший элемент начинает немедленно восстанавливаться.
Для электротехнического оборудования принято выделять четыре составляющих времени восстановления:
t=tОБ + tOP + tЛ + tOВ ,
где tOБ – время обнаружения; tOP – время организации; tЛ – время ликвидации отказа; tO В – время опробывания и включения в работу.
Поскольку каждая составляющая представляет собой случайную величину со своим законом распределения, интенсивность восстановления являются величиной не постоянной. Однако на основании теоремы теории восстановления с достаточной точностью можно воспользоваться показательным законом распределения. Интенсивность восстановления определяется по данным статистического ряда Z1 ...Zn , где Zi – время восстановления после отказа. Интенсивность восстановления
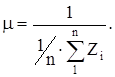 (2.1)
(2.1)
Интенсивность восстановления всех элементов схемы была рассчитана в главе1.
Для системы из n последовательно соединенных восстанавливаемых элементов суммарная интенсивность отказав цепи может быть найдена по выражению
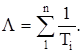 (2.2)
(2.2)
Среднее время безотказной работы последовательной цепи
ТСР = 1/L. (2.3)
Среднее время восстановления
tСР
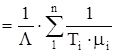 (2.4)
(2.4)
Вероятность безотказной работы системы из n последовательно соединенных элементов на интервале времени от 0 до t0
P=e - L t (2.5)
Коэффициент готовности
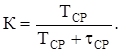 (2.6)
(2.6)
При расчете учитываем, что сами шины и вводные выключатели на 6 и 10 кВ одинаковые, и будем рассматривать надежность электроснабжения по одному из низших напряжений, упростим исходную схему рис.2. до расчетной рис.3.
Рассчитаем последовательные звенья схемы, представленной на рис.3. Так как схема состоит из двух одинаковых в отношении надежности параллельных ветвей, то проведем расчет только для одной ветви. Упростим схему для этого каждую последовательную цепочку заменим на эквивалентный в отношении надежности элемент Э1 иЭ2 см рис.4. Тогда заменим последовательно соединенные элементы: Л1.1, Л1.2, Р1, О1, КЗ1, Т1.1, Т1.2, Ш1, В1.1, В1.2, Ш3 на эквивалентный элемент Э1 см рис.4. Характеристики надежности данного элемента определим по выражениям (2.2)...(2.6).
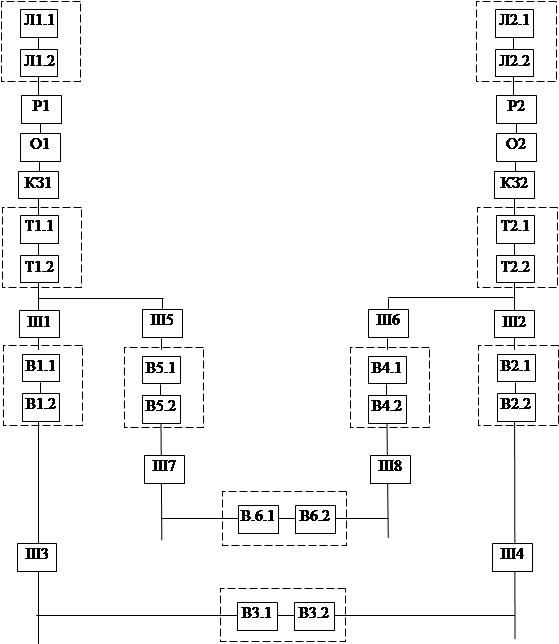 |
Рис. 2. Схема электроснабжения в отношении надежности
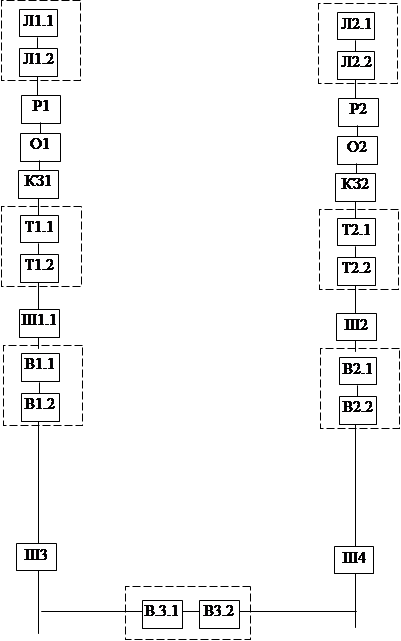
Рис. 3. Упрощенная схема электроснабжения в отношении надежности
Интенсивность отказов
=l /ТЛ1.1 +l /ТЛ1.2 +1/ТР1 +1/ТО1 +1/ТКЗ1 +1/ТТ1.1 +1/ТТ1.2 +1/ТШ1 +1/ТВ1.1 +
+1/ТВ1.2 +1/ТШ3 =5.8/1699440 +5.8/2899560+1/61320 +1/33848 +1/34984 +1/40974 +1/56209 +1/878224 +1/11212 +1/13320 +1/878224=0.000289 , ч-1 .
Среднее время безотказной работы последовательной цепи
ТСР = 1/L=1/0.000289=3460, ч
Среднее время восстановления
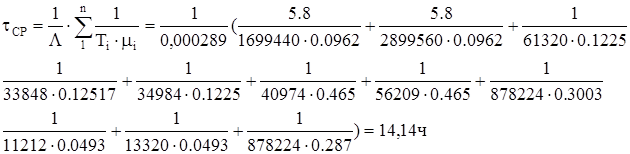
Интенсивность восстановления можно определить как величину, обратную среднему времени восстановления
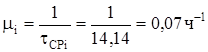
Коэффициент готовности
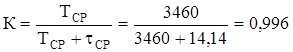
Секционный выключатель, представленный в отношении надежности как два последовательно включенных элемента заменим на один эквивалентный Э1 см. рис.4., и произведем его расчет.
Интенсивность отказов
=1/ТВ3.1 +1/ТВ3.2 =1/10516 +1/12350=0.000176 , ч-1 .
Среднее время безотказной работы последовательной цепи
ТСР = 1/L=1/0.000176=5679, ч
Среднее время восстановления
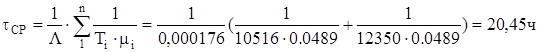
Интенсивность восстановления можно определить как величину, обратную среднему времени восстановления
 |
Рис.4. Эквивалентная схема
 |
Рис. 5. Преобразованная эквивалентная схема
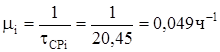
Коэффициент готовности
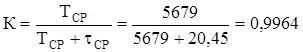
Далее определим параметры последовательного соединения элементов Э1 и Э2 по выражениям (2.2)-(2.6)
Интенсивность отказов
L=1/ТЭ1 +1/ТЭ2 =1/3460 +1/5679=0.000465 , ч-1 .
Среднее время безотказной работы последовательной цепи
ТСР = 1/L=1/0.000465=2150, ч
Среднее время восстановления
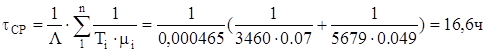
Интенсивность восстановления можно определить как величину, обратную среднему времени восстановления
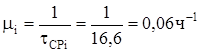
Коэффициент готовности
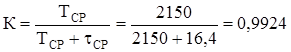
Схема преобразуется к виду, представленному на рис.5.
2.2. Учет резервирования
Анализ систем параллельно соединенных восстанавливаемых элементов будем проводить с учетом четырех условий:
- резервный элемент работает в нагруженном режиме;
- восстановление отказавших элементов не ограниченно;
- во время восстановления в элементах не могут возникать вторичные отказы;
- совпадение моментов наступления двух различных событий считаем практически невозможным.
Интенсивность отказов каждого из элементов Li найдена в предыдущем расчете. Интенсивность восстановления можно определить как величину, обратную среднему времени восстановления
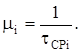 (2.7)
(2.7)
Определим вероятности каждого из четырех состояний для стационарного режима. Система может находиться в четырех состояниях, три из которых являются работоспособными, четвертое – отказ:
- оба элемента работают;
- отказал первый элемент;
- отказал второй элемент;
- отказали оба элемента.
Вероятность первого состояния
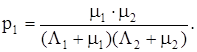
Вероятность второго состояния
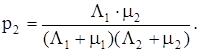
Вероятность третьего состояния
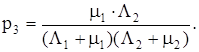
Вероятность четвертого состояния
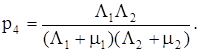
Коэффициент готовности системы
КS = p1 +p2 +p3 .
Коэффициент простоя системы
RS = p4 . (2.8)
Но можно сделать проще и рассчитать только коэффициент простоя, а коэффициент готовности найти как:
КS = 1 - p4 .
Вероятность четвертого состояния
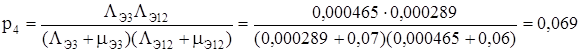
Коэффициент простоя:
КS = 1 - p4 = 1-0,069=0,93
Интенсивность отказа системы из двух взаиморезервирующих элементов
LS = LЭ3 RЭ3 + LЭ12 RЭ12 = 0,000289(1-0,996)
+0,000465(1-0,9924)=0,00000469
Среднее время безотказной работы системы
ТСР S = 1/LS = 1/0,00000469=213219 ч
Для большей части элементов электрических систем отношения l/m=10-3 ...10-4 , поэтому в пределах t 4...5tB справедливо соотношение
MS = MЭ3 +MЭ12 = 0,07+0,06 = 0,13
Поскольку ограничение на восстановление не вводилось, то
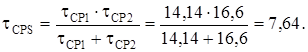 ч
ч
ЗАКЛЮЧЕНИЕ
Результаты вычислений показывают, что существующая схема подстанция Южная обладает достаточной надежностью. Среднее время безотказной работы системы составляет 213219 ч – 24,3 г. Система имеет коэффициент стационарной готовности равный 0,93.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК ИСПОЛЬЗОВАННЫХ
ИСТОЧНИКОВ
1. Фокин Ю.А., Туфанов В.А. Оценка надежности систем электроснабжения. - М.: Энергоатомиздат, 1981.-224с.
2. Розанов М.Н. Надежность электроэнергетических систем. – М.: Энергоатомиздат, 1984. – 200с.
3. Р. Хэвиленд Инженерная надежность и расчет на долговечность. М.: Энергия, 1966. – 232с.