Расчет ребристой плиты перекрытия, расчет неразрезного ригеля
СОДЕРЖАНИЕ: МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ТВЕРСКОЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА «Конструкции и сооружения» КУРСОВАЯ РАБОТА по дисциплине «Железобетонные конструкции»МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ТВЕРСКОЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
КАФЕДРА «Конструкции и сооружения»
КУРСОВАЯ РАБОТА
по дисциплине «Железобетонные конструкции»
на тему:
«Расчет ребристой плиты перекрытия, расчет неразрезного ригеля»
Вариант 15
Выполнил: студент группы ПГС-42
Проверил: Абрамов Л.М.
Тверь 2011
Содержание: стр
1.12Задание …………………………………………………………………………………..3
1.2.Исходные данные ………………………………………………………………………..3
1.3.Конструктивные размеры плиты………………………………………………………..4
1.4.Расчет плиты перекрытия ……………………………………………………………….5
1.4.1.Статический расчет элементов плиты………………………………………………...5
1.4.2.Расчетная схема элементов плиты………………………………………………….…6
1.4.3. Определение усилий в элементах плиты……………………………………………..9
1.5.Расчет элементов плиты по прочности…………………………………………………10
1.5.1.Расчет полки плиты……………………………………………………………………10
1.5.2.Расчет поперечного ребра…………………………………………………………......13
1.5.3.Расчет продольного ребра…………………………………………………….…….…17
1.5.4.Определение геометрических характеристик приведенного сечения…………...…19
1.5.5.Определение потерь в напряженной арматуре………………………………………20
1.6.Расчет плиты на образование трещин нормальной продольной оси элемента…..….21
1.6.1.Расчет на трещиностойкость в стадии обжатия бетона…………………………..…21
1.6.2.Расчет на трещиностойкость в стадии эксплуатации…………………………….....22
1.6.3.Проверка ширины раскрытия трещины…………………………………………..….22
1.7.Расчет прогиба плиты………………………………………………………………..….23
1.8.Расчет ригеля……………………………………………………………………….……24
1.8.1.Статический расчет ригеля……………………………………………………….…..25
1.8.2.Расчет на прочность при изгибе………………………………………………….…..27
1.8.3.Определение прочности ригеля по наклонным сечениям………………………….28
1.9.Построение эпюры материалов………………………………………………..………29
Список литературы
Приложение
1.1.Задание
Рассчитать по прочности все элементы ребристой плиты перекрытия: полку,
Продольные и поперечные ребра. Для продольных ребер плиты выполнить расчет по трещиностойкости в нормальных сечениях и по деформациям.
1.2.Исходные данные
(Вариант №15)
Рассчитать и спроектировать многоэтажное промышленное здание с сеткой колонн 6х6 м; с высотой этажа 3,6м; количество этажей 5; длина цеха 66м.
Покрытие – плита ребристая, ширина номинальная 1,5м, конструктивная 1,48-1,49м
Нагрузка на плиту:
Длительная – 900 кгс/м2
Кратковременная - 200 кгс/м2
Тип ригеля – прямоугольное сечение; класс бетона – В30; класс рабочей арматуры – А800;
Нагрузка от собственного веса пола – 180 кгс/м2;
Расчетный пролет ригеля – крайний;
Бетон В30 исходные механические характеристики:
- Rb = 17,0 МПа;
- Rbt = 1,20 МПа;
- Rbtser = 1,80 МПа;
- Eb = 29000 МПа;
- ![]() = 2500 кг/м3
;
= 2500 кг/м3
;
Арматура А-800:
-![]()
- Rsn = 785 МПа;
- Es = 2,0 * 105 МПа.
1.3.Конструктивные размеры плиты
Компоновка участка перекрытия производиться с учетом требований унификации объемно-планирвочных решений и унификации основных элементов здания. Примеры компановки участка перекрытия, в дальнейшем уточняют расчетом.
Геометрические размеры плиты 1П6 согласно ГОСТ 27215-87 равны:
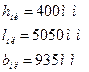
Ширина продольных ребер принимаем: понизу 80 мм, поверху 120 мм.
Расчетная схема в виде таврового сечения.
Рис. 1 Схема расположения колонн и ригелей
1.4.Расчет плиты перекрытия
1.4.1.Статический расчет элементов плиты
Для определения усилий используем исходные данные по нормативным нагрузкам в соответствии с таб. 1.2. СНиП 2.01.07-85*. Нагрузки определяем в форме таб. 1.
Таблица 1
Исходные данные для расчета полки плиты.
| Вид нагрузки | Наименование | Нормативная нагрузка, Н/м2 | Коэффициент надежности по нагрузке i | Коэффициент сочитания нагрузок i | Расчетная нагрузка, Н/м2 |
| Постоянная | От веса пола | 1800 | 1,3 | 1 | 2340 |
| От собственного веса полки плиты s=50мм | 1250 | 1,3 | 1 | 1625 | |
| Временная длительная | V1 | 9000 | 1,2 | 0,95 | 10260 |
| Кратко-временная | V2 | 2000 | 1,2 | 0,9 | 2400 |
| Полная | q1 | 14050 | 16625 |
Для расчета на прочность продольных и поперечных ребер составляем аналогичную таблицу (таб. 2)
Таблица 2
Исходные данные для расчет полки плиты.
| Вид нагрузки | Наименование | Нормативная нагрузка, Н/м2 | Коэффициент надежности по нагрузке i | Коэффициент сочитания нагрузок i | Расчетная нагрузка, Н/м2 |
Постоянная (gi ) |
От веса пола | 1800 | 1,3 | 1 | 2340 |
| От собственного веса всей плиты | 1600 | 1,3 | 1 | 2080 | |
| Временная длительная | V1 | 9000 | 1,2 | 0,95 | 10260 |
Итого длительная: |
12400 |
14680 |
|||
Кратко-временная |
V2 |
2000 | 1,2 | 0,9 | 2160 |
| Полная | q2 | 16840 | |||
Таким образом расчетные значения нагрузок нами определены.
1.4.2. Расчетная схема элементов плиты
Расчетная схема полки плиты и эпюра изгибающих моментов представлена на рис.2
Рис.2.Расчетная схема полки плиты и Рис.3.Расчетные схемы поперечного ребра эпюры изгибающих моментов.
При создании расчетных схем полки и ребер необходимо учитывать их геометрически и нагрузки, приходящиеся на них.
Полку плиты рассчитывают как прямоугольную пластину, опирающуюся по контуру .
Определяем расчетную схему поперечного ребра и максимальный силовой фактор, возникающий в поперечном ребре.
Рис.4.Сечение поперечного ребра.
Согласно нормативным рекомендациям расчетную схему поперечного ребра принимаем в виде таврового сечения.
Рис.5.Расчетная схема поперечного ребра
Определяем ширину стенки поперечного сечения:
![]()
При условии , что ![]() , величину свеса принимают не более 1/6 пролета поперечного ребра.
, величину свеса принимают не более 1/6 пролета поперечного ребра.
![]()
принимая, что высота поперечного ребра равна половине высоты продольного ребра
![]()
Тогда общая ширина будет равна
![]()
Исходя из практики расчета, расчетную схему ребра принимают как балку на 2-х опорах с равномерно распределенной нагрузкой от собственного веса ребра.
Дополнительно к нагрузке от собственного веса ребра прибавляют нагрузку от собственного веса полки.
Рис.6. Расчетная схема поперечного ребра с учетом действующих нагрузок
В расчетной схеме продольного ребра аналогично предыдущему случаю приводим поперечное сечение всей плиты к тавровому.
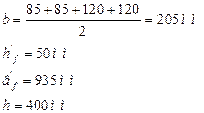
Рис. 7 Сечение продольного ребра. Рис.8 Расчетная схема поперечного сечения продольного ребра
Рис.9 Расчетная схема продольного ребра с учетом действующих нагрузок
1.4.3. Определение усилий в элементах плиты
Изгибающие моменты в продольном направлении полки:
![]()
где ![]() - интенсивность равномерно распределенной нагрузки
- интенсивность равномерно распределенной нагрузки
где ![]() - интенсивность равномерно распределенной нагрузки
- интенсивность равномерно распределенной нагрузки
Нагрузка на поперечное ребро:
![]()
Где qсв - нагрузки от собственного веса поперечного ребра.
![]() кН/м.
кН/м.
Максимальный изгибающий момент в середине пролета поперечного ребра определяют в виде:
![]()
Максимальная перерезывающая сила у опор:
![]()
Максимальный изгибающий момент в середине пролета продольного ребра:
![]()
Максимальная поперечная сила в продольном ребре:
![]()
Для расчета плиты по второй группе предельных состояний необходимо определить расчетные изгибающие моменты от полной и длительной нормативной нагрузок для продольного ребра. Тогда расчетный изгибающий момент от полной нормативной нагрузки определится в виде:
![]()
Где n =1,5- коэффициент надежности.
![]()
Расчетный изгибающий момент от длительной изгибающей нагрузки:
![]()
1.5. Расчет элементов плиты по прочности
1.5.1. Расчет полки плиты
Рассматривая расчетную схему полки плиты, вырезаем из полки элемент шириной 1м и длинной большей из двух значений продольного и поперечного ребра.
Рис.10 Расчетная схема полки плиты
Полку плиты армируют сварными сетками с рабочей арматурой в том или ином направлении.
Для рассматриваемого случая h=50мм, h0 =2,5см
Определим размер арматуры, используя формулу:
![]()
Где Rb - расчетное сопротивление бетона при сжатии, Rb =17 МПа, b-ширина полки, b=100мм, h0 -рабочая высота сечения полки, h0 =25мм, n =0,95- коэффициент надежности по нагрузке; b2 =0,9 – по техническим характеристикам здания.
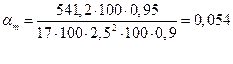
m =0,054 следовательно:
![]()
Определяем положение нейтральной линии:
![]()
![]()
Из неравенства определяем абсолютную граничную высоту сжатой зоны Х
![]()
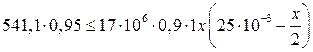
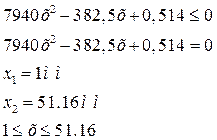
Определим относительную граничную высоту сжатой зоны:
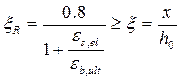
где 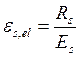 ; для армирования полки плиты принимаем арматуру В500
; для армирования полки плиты принимаем арматуру В500
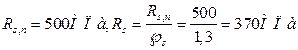
Где - 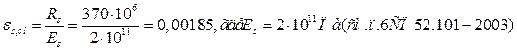
Величину ![]() для всех классов бетона. Тогда:
для всех классов бетона. Тогда:
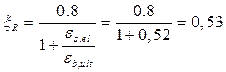
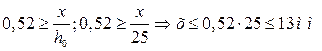
Таким образом, учитывая значения, получившиеся из 2-х неравенств получим: 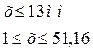 , следовательно, принимаем Х=12мм.
, следовательно, принимаем Х=12мм.
ХR
= ![]() *
* ![]()
ХR = 0,52*25=13
Х ХR - условие выполняется
Условие оптимальности армирования ![]()
![]() выполняется (0,030,), т.е. элемент не является переармированным.
выполняется (0,030,), т.е. элемент не является переармированным.
![]() =1-0,5*
=1-0,5*![]() =1-0,5*0,03=0,985
=1-0,5*0,03=0,985
Определяем площадь поперечного сечения арматуры:
![]()
Где Rs - расчетное сопротивление арматуры растяжению, Rs =370 МПа; s =0,95- коэффициент надежности по арматуре.
![]()
Проверяем площадь арматуры по условию минимальности армирования:
![]() , т.е. указанная площадь арматуры удовлетворяет условию минимальности армирования.
, т.е. указанная площадь арматуры удовлетворяет условию минимальности армирования.
Исходя из технологический требований условия сварки принимают минимальный диаметр рабочей арматуры 6 мм. Согласно СП52-101-2003 расстояние между осями стержней (п.8.3.6) следует принять равным 200 мм.
Определим общее количество продольных стержней, исходя из общей ширины полки плиты: 935/200=4,68. Принимаем 5 стержней.
Определим общее количество поперечных стержней: 5050/200=25,25. Принимаем 26 стержней. Наименьший допустимый диаметр 3 мм (табл. 10 методического пособия).
Таким образом, для армирования полки принимаем сетку С1 со следующими конструктивными размерами: 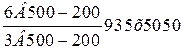
1.5.2. Расчет поперечного ребра
Поперечное ребро рассчитывают на изгиб, как балку таврового поперечного сечения с одинарной арматурой.
Рис.11. Расчетная схема поперечного ребра. Тавровое сечение.
![]()
Составим уравнение моментов относительно оси Х1:
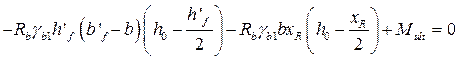
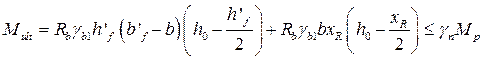
![]()
Решая данное неравенство, получаем: ![]() мм .
мм .
Определим относительную граничную высоту сжатой зоны:
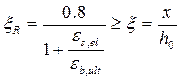
где 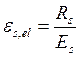 ;
;
обычно для поперечного ребра принимают арматуру В500.
Где - 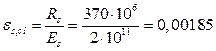
Величину ![]() для всех классов бетона. Тогда:
для всех классов бетона. Тогда:
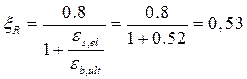
Выбираем х так, чтобы удовлетворялось неравенство: ![]()
![]()
Где ![]()
![]()
![]()
Таким образом, учитывая значения, получившиеся из 2-х неравенств получим: ![]() , следовательно, принимаем Х=90 мм.
, следовательно, принимаем Х=90 мм.
ХR
= ![]() *
* ![]()
ХR = 0,52*180=93,6
Х ХR - условие выполняется
Условие оптимальности армирования ![]()
![]() выполняется(0,030,52), т.е. элемент не является переармированным.
выполняется(0,030,52), т.е. элемент не является переармированным.
Для того, чтобы найти площадь арматуры, составим уравнение моментов, относительно оси ![]() :
:
![]()
![]()
Проверяем площадь арматуры по условию минимальности армирования:
![]()
Т.к. условие минимальности армирования выполняется, то принимаем ![]()
![]()
Согласно таб.9 [1] определяем размеры поперечного сечения рабочей арматуры![]() . Рабочая арматура поперечного ребра А1000
. Рабочая арматура поперечного ребра А1000![]() .
.
Выполним проверку необходимости наличия поперечной арматуры (расчет ведут по величине поперечной силы).
![]() , где
, где ![]() для всех случаев
для всех случаев
![]()
![]()
Условие выполняется.
Выполняем проверку по перерезывающей силе в опасном наклонном сечении:
Условие прочности имеет следующий вид: ![]() , где
, где
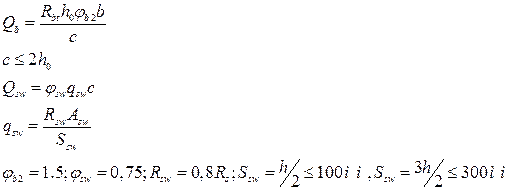
![]() - расчетное сопротивление растяжению;
- расчетное сопротивление растяжению;
![]() - площадь поперечного сечения всех поперечных стержней, попадающих в наклонное сечение. (предварительно принимаем арматуру А240 d=6мм, Asw
=0.283см2
);
- площадь поперечного сечения всех поперечных стержней, попадающих в наклонное сечение. (предварительно принимаем арматуру А240 d=6мм, Asw
=0.283см2
);
Sw
– шаг поперечной арматуры (в приопорной зоне ![]() , в пролетной зоне
, в пролетной зоне ![]()
![]()
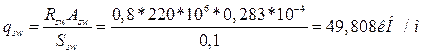
![]() кН
кН
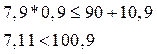 , т.е. усилие, воспринимаемое балкой, больше чем фактическое усилие.
, т.е. усилие, воспринимаемое балкой, больше чем фактическое усилие.
Так условие соблюдается, то нет необходимости увеличивать диаметр прутков поперечной арматуры.
Проверку по наклонным сечениям, выполняемую по величине изгибающего момента не производят, если вся продольная арматура установленная, исходя из прочности по нормальным сечения, полностью доведена до опоры, а также если арматура на свободной опоре имеет анкеровку.
В качестве поперечной арматуры используем А 240 d=6мм, с шагом в приопорной зоне-100мм, в пролетной зоне-150мм.
Рис. 12. Схема балки для расчета перерезывающей силы в наклонном сечении
1.5.3. Расчет продольного ребра
Рис.13. Расчетная схема продольного ребра
Плиты П-образного сечения изготавливают предварительно напряженными.
Для предварительного напряжения арматуры определяют класс и величину предварительного напряжения.
Выбор напряженной арматуры для продольного ребра производим согласно [3] п.2.2.1.3. Выберем арматуру А1000, по таб.7 [3] Rsn
=980МПа. По [3] п.2.2.3.1. выбираем предварительное напряжение ![]() для горячекатаной и термомеханически упрочненной;
для горячекатаной и термомеханически упрочненной; ![]() для холодноармированных и канатов. Мы используем стержневую горячекатаную арматуру. Поэтому принимаем
для холодноармированных и канатов. Мы используем стержневую горячекатаную арматуру. Поэтому принимаем ![]()
При определении величины предварительного натяжения необходимо учитывать точность натяжения арматуры.
![]() неблагоприятное влияние арматуры;
неблагоприятное влияние арматуры;
![]() благоприятное влияние арматуры
благоприятное влияние арматуры
С учетом благоприятного действия имеем окончательное значение ![]()
Т.к. арматура установлена и в растянутой и в сжатой зоне элемента, то необходимо выполнить расчет как для элементов с двойной арматурой.
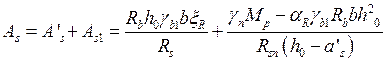
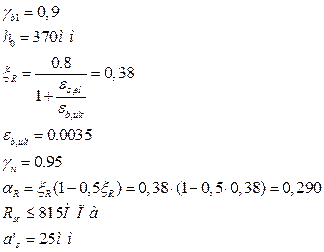
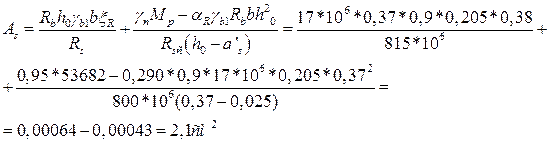
Согласно таб.9 [1] определяем размеры поперечного сечения арматуры. Ближайшее большее значение ![]() , т.е. рабочая арматура продольного ребра – 2 стержня класса А1000 d=12мм
, т.е. рабочая арматура продольного ребра – 2 стержня класса А1000 d=12мм
Расчет продольного ребра на действие поперечных сил ведем аналогично предыдущему пункту:
1.Расчет по полосе между наклонными сечениями.
![]()
Где ![]() =0,3 ;
=0,3 ; ![]() =0,9
=0,9
![]()
![]()
Условие выполняется.
2.Расчет по наклонным сечениям на действие поперечных сил
![]() ,
,
Где ![]()
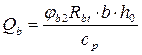 , поперечная сила воспринимаемая бетоном в наклонном сечении
, поперечная сила воспринимаемая бетоном в наклонном сечении
![]()
Где ![]() =1,5 ,
=1,5 , ![]()
![]()
Где ![]() - коэффициент принимаемый равным 0,75;
- коэффициент принимаемый равным 0,75;
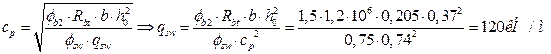 ,
,
![]()
![]()
В качестве поперечной арматуры используем А1000 d=6мм, с шагом в приопорной зоне-150мм, в пролетной зоне-300мм.
Рис.14.Схема продольного ребра для расчетов по наклонным сечениям.
1.5.4. Определение геометрических характеристик приведенного сечения
Рис.15.расчетная схема для определения геометрических характеристик приведенного сечения продольного ребра
Площадь приведенного сечения плиты:
![]()
где 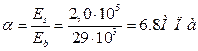
![]() см2
см2
Статический момент приведенного сечения относительно нижней грани:
![]()
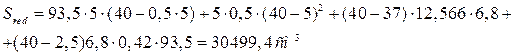
Расстояние от нижней грани до центра тяжести приведенного сечения:
![]() см2
см2
Момент инерции приведенного сечения:
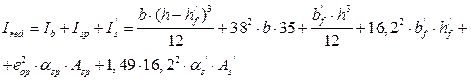
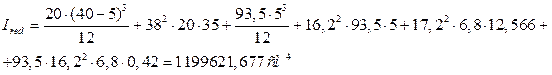
Определяем момент сопротивления приведенного сечения для волокон нижней зоны.
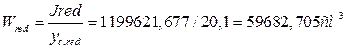
Таким образом, мы определили геометрические характеристики и центр тяжести приведенного сечения.
1.5.5. Определение потерь в напряженной арматуре
Определим потери напряжения в арматуре:
- Потери от релаксации напряжений в арматуре:
![]() , принимая механический способ
, принимая механический способ
- Потери от температурного перепада:
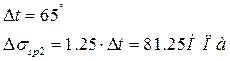
- Потери от деформации формы:
При неизвестности конструкции формы по нормам 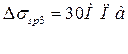
- Потери от деформации анкера:
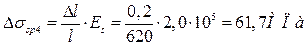
- Потери от усадки:
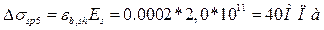 , где
, где 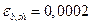 для бетона В30.
для бетона В30. - Потери от ползучести:
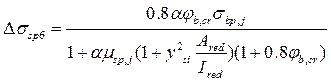
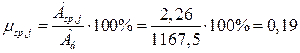 - коэф. армирования элемента напрягаемой арматуры;
- коэф. армирования элемента напрягаемой арматуры;
![]() =1,9 - коэффициент ползучести согласно СП 52-101-2003 табл.5.5;
=1,9 - коэффициент ползучести согласно СП 52-101-2003 табл.5.5;
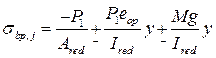 берется на уровне расположения арматуры;
берется на уровне расположения арматуры;
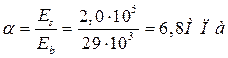
![]()
![]() - площадь поперечного сечения напряженных стержней;
- площадь поперечного сечения напряженных стержней;
![]() - сумма всех потерь до 5
- сумма всех потерь до 5
![]()
![]()
![]()
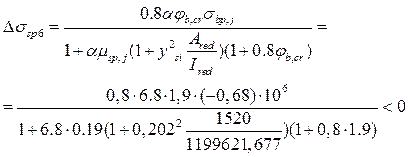
Значение потери от ползучести меньше нуля, значит мы условно принимаем их нулевыми.
1.6. Расчет плиты на образование трещин нормальной продольной оси элемента
1.6.1. Расчет на трещиностойкость в стадии обжатия бетона
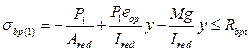
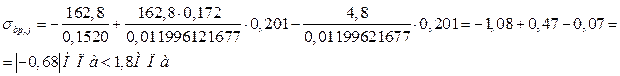
Условие выполняется, значит трещин не возникает.
1.6.2. Расчет на трещиностойкость в стадии эксплуатации
Проверку на трещиностойкость выполняют по величине момента начала образования трещин (Mcrc).
![]() ,
,
где ![]() - нормативное значение изгибающего момента в расчетном сечении;
- нормативное значение изгибающего момента в расчетном сечении;
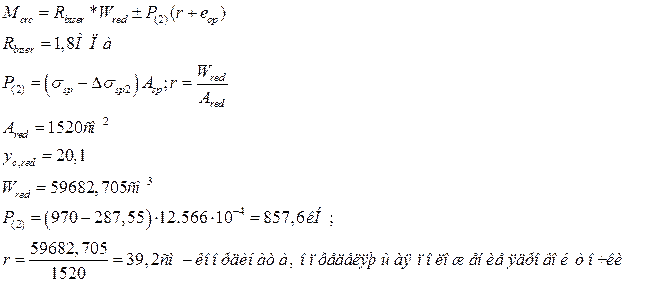
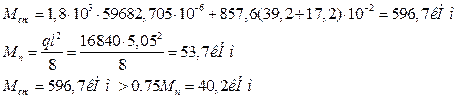
Условие не выполняется, т.е. моменты образования трещин при данной внешней нагрузке не возникнет, а значит и трещины не появятся. В этом случае проверку по раскрытию трещин не выполняют, но в учебных целях мы произведем этот расчет.
1.6.3. Проверка ширины раскрытия трещины
![]()
где![]() -фактическая ширина раскрытия трещины;
-фактическая ширина раскрытия трещины;
![]() -предельная ширина раскрытия трещины, нормируемая
-предельная ширина раскрытия трещины, нормируемая
СП-52-102-2004;
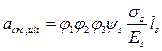
где ![]() - коэффициент, учитывающий продолжительность действия нагрузки; при продолжительном действии
- коэффициент, учитывающий продолжительность действия нагрузки; при продолжительном действии ![]() =1,4;
=1,4;
![]() - коэффициент, учитывающий профиль арматуры;
- коэффициент, учитывающий профиль арматуры; ![]() =0,5;
=0,5;
![]() - коэффициент, учитывающий вид нагружения;
- коэффициент, учитывающий вид нагружения; ![]() при изгибе со сжатием;
при изгибе со сжатием;
![]() - коэффициент, учитывающий неравномерность распределения деформации между трещинами;
- коэффициент, учитывающий неравномерность распределения деформации между трещинами;
![]() в начальном расчете, проверяют условия раскрытия трещины по нормативным значениям, если оно не выполняется, то
в начальном расчете, проверяют условия раскрытия трещины по нормативным значениям, если оно не выполняется, то ![]() ;
;
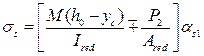
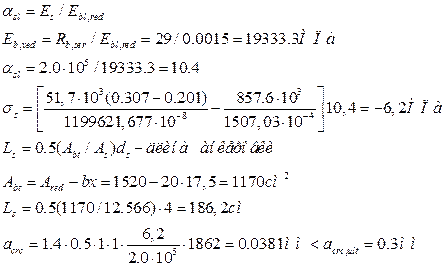
1.7. Расчет прогиба плиты
Расчет прогиба плиты ведут для постоянных длительных нагрузок.
Рис. 16. Расчетная схема для определения прогиба плиты
Расчет прогиба плиты осуществляют в следующем виде:
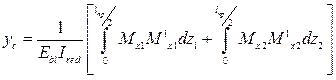 где
где
![]()
![]()
![]()
![]()
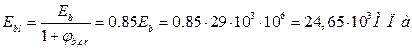
Таким образом, подставив все вышеперечисленное в выражение, получим
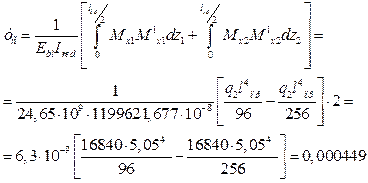
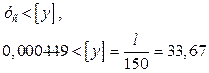
Прогиб плиты меньше допустимого прогиба.
1.8. Расчет ригеля
В качестве расчетной схемы ригеля принимаем неразрезную трехпролетную балку с равномерно распределенной нагрузкой.
Рис. 17. Габаритная схема ригеля
1.8.1. Статический расчет ригеля
Определение длины пролётов:
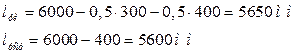
Постоянная нагрузка на один погонный метр по длине определяется в следующем виде:
![]() , где
, где
![]() - суммарный вес нагрузок от веса плит, от веса пола и собственного веса ригеля;
- суммарный вес нагрузок от веса плит, от веса пола и собственного веса ригеля;
![]()
![]() - нагрузка от собственного веса ригеля
- нагрузка от собственного веса ригеля
![]()
![]() - временная нагрузка
- временная нагрузка
![]()
Значения ![]() берем из таб.1 и таб.2
берем из таб.1 и таб.2
![]()
![]()
![]()
![]()
Таким образом, мы определили суммарную нагрузку на 1м ригеля.
Эпюру ![]() строим на основе эмпирических данных, полученных с учетом деформирования бетона под действие внешних нагрузок.
строим на основе эмпирических данных, полученных с учетом деформирования бетона под действие внешних нагрузок.
![]()
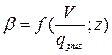
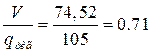
Делим пролет на 5 равных частей и для каждой части вычисляем свой момент.
Значение моментов нижней ветви, огибающей эпюру, рассчитываем по формулам:
Изгибающие моменты в первом пролёте:
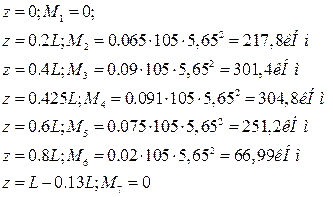
Определим нулевую точку верхней эпюры:
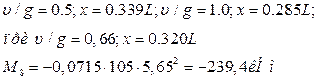
Рис. 18. Эпюра изгибающих моментов
Значение перерезывающей силы рассчитываем по формулам:
![]()
![]()
Рис.19. Эпюра перерезывающих сил ригеля
1.8.2. Расчет на прочность при изгибе
Предварительно определяем высоту ригеля в первом пролёте:
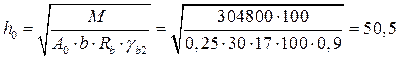
Принимаем
Окончат. рабочая высота сечения:
Определим относительную граничную высоту сжатой зоны:
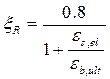
где 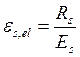 ;
;
Где - 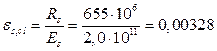
Величину ![]() для всех классов бетона. Тогда:
для всех классов бетона. Тогда:
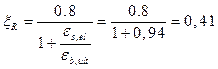
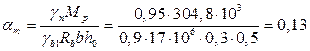
![]()
![]()
Проверяем условие армирования сечения ![]() , т.е. элемент не является переармированным.
, т.е. элемент не является переармированным.
Определяем площадь рабочей арматуры в растянутой зоне
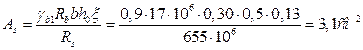
Принимаем 4 стержня d=10мм, А1000, Аs =3,14см2
Определяем величину площади поперечного сечения рабочей арматуры в верхней зоне ригеля на опоре (М=187,48кН·м)

![]()
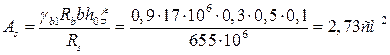
Принимаем 2 стержня d=14мм, А1000, Аs =3,08см2
1.8.3.Определение прочности ригеля по наклонным сечениям
![]()
Где ![]() =0,3 ;
=0,3 ; ![]() =0,9
=0,9
![]()
![]()
Условие выполняется, значит, поперечную арматуру расчитывать не нужно, она устанавливается конструктивно.
В качестве поперечной арматуры конструктивно используем А1000 d=6мм, с шагом приопорной зоне-150мм, в пролетной зоне-300мм.
Рис.20.Поперечное сечение ригеля
1.9. Построение эпюры материалов
Под эпюрой материалов понимается распределение арматуры по длине ригеля. Для построения вычисляем предельное значение изгибающего момента для мест теоретического обрыва.
Величина предельного момента определяется по формуле
![]() .
.
![]() предельный изгибающий момент для рассматриваемого предельного участка;
предельный изгибающий момент для рассматриваемого предельного участка;
![]() площадь поперечного сечения продольной рабочей арматуры на рассматриваемом участке;
площадь поперечного сечения продольной рабочей арматуры на рассматриваемом участке;
![]() расстояние от центра тяжести учитываемой арматуры до горизонтальной центральной оси бетона сжатой зоны.
расстояние от центра тяжести учитываемой арматуры до горизонтальной центральной оси бетона сжатой зоны.
Сечение в пролете
Для сечения в пролете по расчету получили 4 стержня ![]() (
(![]() )
)
![]()
Обрываем 2 стержня ![]() заменяя их на 2 стержня
заменяя их на 2 стержня ![]() (
(![]() )
)
![]()
Сечение на опоре
Для сечения на опоре по расчету получили (![]() )
)
![]()
Определение длины анкеровки обрываемых стержней
Определим длину анкеровки обрываемых стержней, за сечения, совпадающие с точкой теоретического обрыва. Найдем перерезывающие силы в сечениях, соответствующих точкам теоретического обрыва.
Все значения Q, взяты с эпюры Q построенной с помощью графического редактора
![]() 187,79 кН;
187,79 кН;
![]() 220,58 кН;
220,58 кН;
Так как поперечная арматура установлена конструктивно, а не по расчету, то величину заведения стержня арматуры за сечение теоретического обрыва определяем из условия:
![]()
где ![]() - наибольший диаметр стержня продольной рабочей арматуры.
- наибольший диаметр стержня продольной рабочей арматуры.
Для стержней, находящихся в растянутой зоне:
![]()
Для стержней, находящихся в сжатой зоне:
![]()
Рис.21. Эпюра материалов
Список используемой литературы
1. Методическое указание. По расчету панели и ригеля многоэтажного многопролетного промышленного здания. Тверь: ТГТУ , Кафедра “Конструкций и сооружений”, 2006.-15c.
1. СП-52-101-2003. Бетонные и железобетонные конструкции без предварительного напряжения арматуры.
2. СП-52-102-2004. Предварительно напряженные железобетонные конструкции.
3. ГОСТ 23-279.85. Сетки арматурные сварные для железобетонных конструкций и изделий. Общие технические условия.