Реализация и анализ цифрового фильтра с конечной импульсной характеристикой

СОДЕРЖАНИЕ: Министерство образования Российской Федерации УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Оценка работы Курсовая работа Реализация и анализ цифрового фильтра с конечной импульсной характеристикой

Министерство образования Российской Федерации

УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Оценка работы

Курсовая работа

Реализация и анализ цифрового фильтра с конечной импульсной характеристикой

по курсу «Цифровая обработка сигналов»

Преподаватель

Коберниченко В.Г.

Екатеринбург


ЗАДАНИЕ

Тема 2. Реализация и анализ цифрового фильтра с конечной импульсной характеристикой

Задание:

1. Разработать алгоритм, реализующий заданный тип фильтра в частотной области (с использованием алгоритма БПФ).

2. Составить программу, позволяющую получить:

- спектр входного сигнала;

- спектральную (амплитудно-частотную) характеристику окна;

- отклик фильтра на заданный сигнал;

- спектр выходного сигнала.

3. Проанализировать полученные результаты.

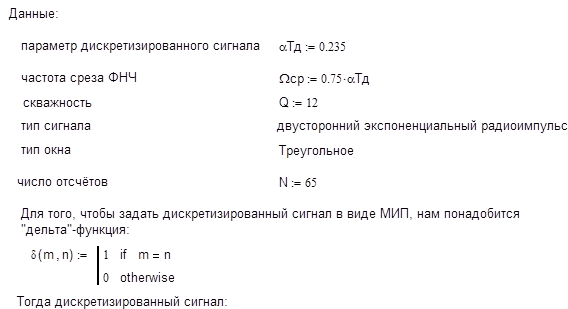
Исходные данные

Номер варианта: 7

Тип фильтра: ФНЧ

Полоса фильтра: 0,75

Тип окна: треугольное

Вид сигнала: двусторонний экспоненциальный радиоимпульс с несущей частотой, равной половине частоты дискретизации.

Скважность: 12


РЕШЕНИЕ

1. Математическая модель сигнала.

где Ф(t) – функция Хевисайда

w0 – несущая частота

Дискретный сигнал:

Для того, чтобы можно было построить спектр входного сигнала, необходимо выразить произведение , исходя из требования обеспечения уровня неопределённости (наложения спектров) не хуже –13 дБ. Наложение спектров происходит вследствие дискретизации сигнала, которая приводит к периодизации спектра с частотой . Для определения необходимо найти энергию, распределённую на участке от нуля до половины частоты дискретизации и энергию, распределённую в диапазоне от половины частоты дискретизации до бесконечности.

Так как спектр радиоимпульса отличается от видео только тем, что он сдвинут на несущую частоту, можно найти из условия наложения спектров видеоимпульса. Спектр исходного сигнала без заполнения определяется соотношением:


,

взяв квадрат модуля, получим энергию сигнала:

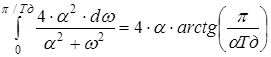
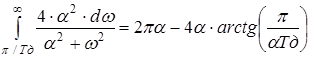
Соотношение этих энергий и будет задавать требуемый уровень неопределённости:

Решив это уравнение, получаем, что = 0,235.

Для того, чтобы найти количество отсчетов в периоде повторения, найдем эффективную длительность импульса:

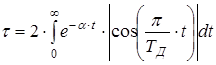
Тогда количество отсчетов на периоде повторения будет равно:

N = tQFД ,


где Q – скважность.

Получаем,

N = tQFД = 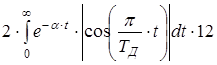= 64,817 65

Определим верхнюю частоту спектра сигнала из условия половинной мощности:

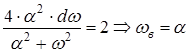
По условию задается, что полоса фильтра определяется по уровню 0,75 от полосы спектра сигнала, следовательно, она будет равна 0,75a

Далее приведем основной расчет







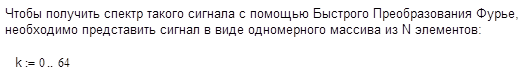
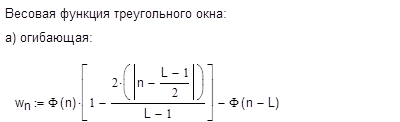
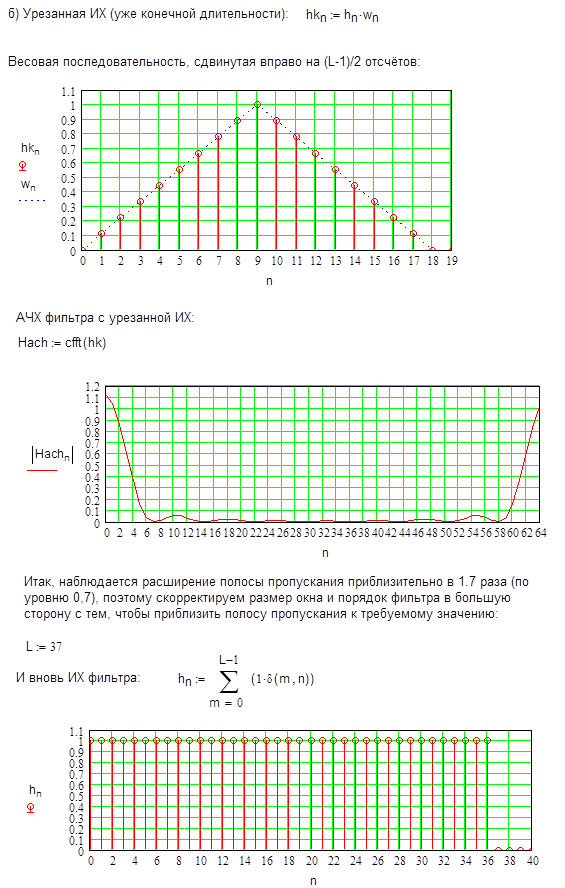
Видим, что сигнал был отфильтрован.

Посмотрим, как будет реагировать однородный фильтр (без учета окна):

Спектр сигнала на выходе такого фильтра будет иметь вид:


Тогда сам сигнал:

Видим, что сигнал отфильтрован хуже, чем при введении весовой функции окна.

Проведем анализ полученного фильтра во временной области:

Отклик на входной сигнал равен свертке от входного сигнала и импульсной характеристики фильтра.

Тогда сигнал на выходе фильтра будет иметь вид:


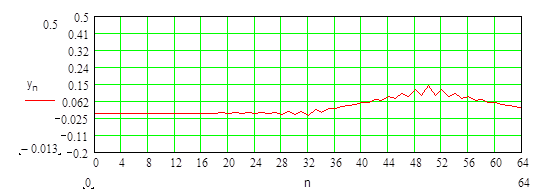
Выводы: В ходе выполнения данной курсовой работы был разработан алгоритм, реализующий заданный тип фильтра (ФНЧ) как во временной так и в частотной областях с учетом весовой функции и без неё. Был получен отклик фильтра на заданный сигнал и его спектр.

Скачать архив с текстом документа