Структурная схема и управление электроприводом
СОДЕРЖАНИЕ: Разработка структурной схемы для системы Управляемый выпрямитель - автономный инвертор напряжения – асинхронный двигатель. Проверка системы автоматического управления на устойчивость с помощью критериев устойчивости (Гурвица, Найквиста, Михайлова).Ульяновский Государственный Технический Университет
Кафедра «Электропривод и автоматика ПУ и ТК»
Курсовая работа
по дисциплине
Теория автоматического управления
Структурная схема и управление электроприводом
Выполнил: ст. гр.Ад-41
Сапунов Н.Е.
Ульяновск 2010
Содержание
Описание задания на курсовую работу
1. Описание САУ переменного тока
2. Статические характеристики САУ переменного тока
2.1 Математическое описание преобразователя частоты (ПЧ) с промежуточным звеном постоянного тока на основе АИН
2.2 Математическое описание асинхронного двигателя при управлении частотой и напряжением статора
2.3 Статические характеристики САУ на основе АД
2.3.1 Статические характеристики САУ при ![]()
2.3.2 Статические характеристики САУ при ![]()
2.3.3 Статические характеристики САУ при вентиляторной нагрузке
3. Динамические характеристики САУ переменного тока
4. Анализ устойчивости САУ
4.1 Критерий устойчивости Гурвица
4.2 Критерий устойчивости Найквиста
4.3 Критерий устойчивости Михайлова
4.4 Построение ЛАЧХ и ФЧХ
5. Расчет переходного процесса
6. Вывод
7. Список литературы
Описание задания на курсовую работу
Целью данной курсовой работы является получение практических навыков по построению структурной схемы для системы «Управляемый выпрямитель - автономный инвертор напряжения – асинхронный двигатель», и ее дальнейшее упрощение с целью получения передаточной функции по управляющему воздействию (xf и xu ). Проверка системы автоматического управления с помощью критериев устойчивости. И построение графиков переходного процесса.
Исходные данные:
САУ переменного тока. Настройка на симметричный оптимум.
| Uф.с.м , В | nc , об/мин | rc , Ом | xc , Ом | rp ’, Ом | xp ’, Ом |
| 220 | 875 | 3,6 | 2,58 | 5,7 | 2,63 |
1. Описание САУ переменного тока
Развитие полупроводниковой преобразовательной техники привело к широкому использованию электроприводов с электродвигателями переменного тока, к созданию новых систем управления этими электродвигателями. По сравнению с системами управления электроприводами постоянного тока системы управления электроприводами переменного тока значительно более разнообразны. В регулируемых электроприводах используются асинхронные электродвигатели с короткозамкнутым или фазным ротором, синхронные и вентильные электродвигатели. Применяются различные способы регулирования скорости электродвигателя путем изменения: напряжения статора, частоты и напряжения статора, частоты и напряжения ротора, добавочного сопротивления в цепи ротора и др. Используется значительно большее число регулируемых координат, чем в электроприводах постоянного тока. Вместе с тем имеются определенные ограничения в использовании того или иного способа управления и созданной на основе этого способа системы управления электродвигателем. Все эти обстоятельства затрудняют формирование общих подходов к синтезу АСУ ЭП переменного тока в такой степени, как это было сделано в АСУ ЭП постоянного тока.
Управление электродвигателями переменного тока осложнено рядом обстоятельств, наиболее существенными из которых являются следующие: 1) момент электродвигателя определяется произведением двух результирующих векторов электромагнитных параметров статора и ротора и является функцией четырех переменных; 2) имеется сильное взаимодействие намагничивающих сил статора и ротора, взаимное состояние которых непрерывно меняется при вращении ротора; 3) с целью лучшего использования двигателя в различных режимах его работы возникает задача регулирования магнитного потока двигателя.
Электродвигатели переменного тока совместно с управляемыми преобразователями представляют собой сложные многосвязные нелинейные объекты управления. Полное математическое описание таких объектов оказывается довольно громоздким и неприменимым для инженерных методов синтеза систем управления. Вместе с тем в практике построения систем электроприводов, включая и АСУ ЭП переменного тока, получили распространение простые приемы синтеза систем управления, основанные на принципах подчиненного управления и на использовании унифицированных настроек контуров регулирования, входящих в систему управления. Использование этих приемов позволяет не только просто выполнить синтез систем управления, но и создает обоснованную возможность упрощения математического описания электроприводов переменного тока, в частности возможность пренебрежения взаимосвязью ряда координат и параметров электроприводов.
Основная сложность при создании АСУ ЭП переменного тока заключается в создании независимого управления электромагнитным моментом и потоком двигателя. Если это удается выполнить, то АСУ ЭП переменного тока с обратными связями по скорости или по положению выполняются точно так же, как и АСУ ЭП постоянного тока, включая и способы управления пусковыми и тормозными режимами.
При синтезе взаимосвязанных систем управления используются два основных приема, обеспечивающих автономность (независимость) контуров регулирования: а) использование различного рода дополнительных компенсационных связей между локальными контурами регулирования; б) разделение локальных контуров регулирования по быстродействию. Оба этих приема используются при выполнении АСУ ЭП переменного тока, и это дает основание уже на стадии формирования математической модели электропривода делать ряд упрощений.
2. Статические характеристики САУ переменного тока
2.1 Математическое описание преобразователя частоты (ПЧ) с промежуточным звеном постоянного тока на основе АИН
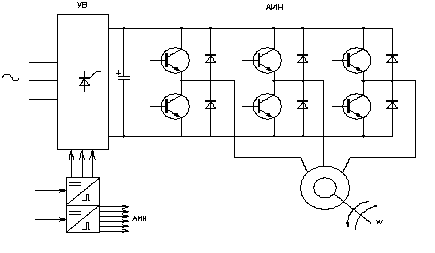
УВ – управляемый выпрямитель, отвечает за напряжение подаваемое на асинхронный двигатель;
АИН – автономный инвертор напряжения, отвечает за частоту подаваемого напряжения на асинхронный двигатель.
Функциональная схема преобразователя частоты
 |
Исходное дифференциальное уравнение

Запишем эти уравнения в операторной форме
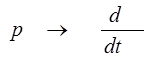

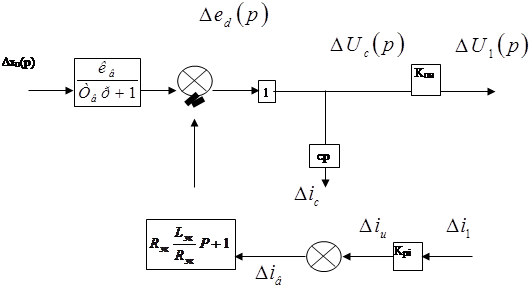
Структурная схема ПЧ на основе АИН.
 |
2.2 Математическое описание асинхронного двигателя при управлении частотой и напряжением статора
При исследовании переходных процессов в трехфазных асинхронных электродвигателях целесообразно принять следующие допущения, позволяющие в доступной математической форме выразить соотношения основных параметров и координат электродвигателя:
1) намагничивающие силы обмоток двигателя распределены синусоидально вдоль окружности воздушного зазора;
2) потери встали статора и ротора отсутствуют;
3) обмотки статора и ротора строго симметричны со сдвигом осей обмоток на 120°;
4) насыщение магнитной цепи отсутствует.
Уравнения равновесия напряжений для обмоток трех фаз статора имеют вид
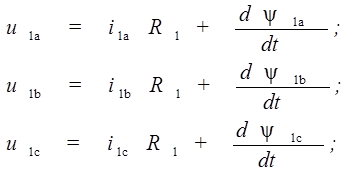 (1)
(1)
Соответственно для обмоток трех фаз ротора
 (2)
(2)
Где ![]() — мгновенные значения фазных напряжений статора и ротора;
— мгновенные значения фазных напряжений статора и ротора;
![]() — мгновенные значения фазных токов статора и ротора;
— мгновенные значения фазных токов статора и ротора;
![]() - полные потокосцепления фазных обмоток;
- полные потокосцепления фазных обмоток;
R1 , R2 — активные сопротивления обмоток статора и ротора.
Асинхронный электродвигатель представляет собой систему магнитно-связанных обмоток, расположенных на статоре и роторе. При вращении ротора взаимное положение обмоток статора и ротора непрерывно изменяется, соответственно изменяется и взаимная индуктивность между ними. С учетом принятых допущений можно считать, что взаимная индуктивность пропорциональна косинусу текущего угла между осями обмоток ротора и статора.
При математическом описании трехфазных асинхронных двигателей удобно оперировать не мгновенным значениями координат, а их результирующими векторами. Если, например, мгновенные значения токов равны ia , ib , ic , то результирующий вектор тока определяется уравнением:
 ,
,
Где a0 =ej 0 =1; a=ej 2 /3 ; a2 = ej 4 /3 .
Аналогично определяются результирующие векторы напряжения
![]()
и потокосцепления
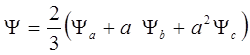
Используя выражения результирующих векторов, уравнения (1) можно записать в виде одного дифференциального уравнения в векторной форме. Для этого первое уравнение из (1) умножается на 2/3a0 , второе на 2/3a, третье на 2/3a2 . Суммируя полученные произведения, получим

или в векторной форме
![]() (4)
(4)
Аналогично векторное уравнение напряжений ротора:
![]() (5)
(5)
В уравнениях (4) и (5) векторы записаны соответственно в системах координат статора и ротора. Для совместного решения уравнений их необходимо привести к одной системе координат.
При исследовании переходных процессов в электродвигателях переменного тока применяют различные ортогональные системы координат, отличающиеся угловой скоростью вращения координатных осей сок, например системы, оси которых неподвижны относительно ротора, или неподвижны относительно статора, или вращаются с синхронной скоростью.
Уравнения асинхронного электродвигателя в системе координат, вращающейся с произвольной скоростью к , имеют вид
 (6)
(6)
где — угловая скорость вращения ротора; pп — число пар полюсов.
При исследовании переходных процессов в асинхронном электродвигателе, управляемом частотой и напряжением статора, удобно использовать систему координат, вращающуюся со скоростью к , равной угловой скорости вращения магнитного поля 0 ’, приведенной к числу пар полюсов, равному единице (приведенной к двухполюсному электродвигателю). Предполагается при этом справедливым равенство
![]() ,
,
где f1 — частота напряжения статора, Гц; 1 — угловая частота напряжения статора, рад/с.
На основании уравнений (6) для рассматриваемой координатной системы можно записать
 (7)
(7)
где s — скольжение электродвигателя:

(0 = 0 ’/pп — угловая скорость вращения магнитного поля, или синхронная скорость электродвигателя).
Потокосцепления связаны с токами через индуктивности
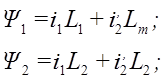 (8)
(8)
Для определения электромагнитного момента асинхронного электродвигателя используется векторное произведение 1 и i1
тогда
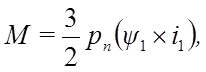 (9)
(9)
или векторное произведение 2 и i2 ’, тогда
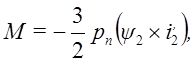 (10)
(10)
Учитывая выражения (8), можно записать (9) и (10) в виде
 ; (11)
; (11)
 . (12)
. (12)
Вторые равенства в уравнениях (11), (12) справедливы потому, что векторное произведение двух одинаково направленных векторов равно нулю.
Для полного описания переходных процессов в асинхронном электродвигателе к уравнениям напряжений и моментов следуй добавить уравнение
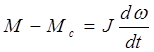 , (13)
, (13)
записанное для скалярных значений моментов М и Мс .
Полученная система уравнений электродвигателя является нелинейной, и решение ее для различных динамических режимов работы электродвигателя может быть выполнено с использованием вычислительных машин. При синтезе систем управления асинхронным электродвигателем целесообразно располагать простыми и наглядными динамическими моделями электродвигателя в виде передаточных функций или структурных схем. Такая возможность появляется, если рассматривать переходные процессы в отклонениях относительно начальных координат электродвигателя.
Сравнительно простая структурная схема может быть получена, если пренебречь активным сопротивлением статорной цепи, т. е. положить R1 =0. Безусловно, что такое пренебрежение накладывает определенные ограничения на использование получаемых моделей. Они вполне применимы для систем с небольшим диапазоном регулирования скорости относительно синхронной скорости, для электродвигателей средней и большой мощности. При широком регулировании скорости, а также для электродвигателей малой мощности необходимы уточнения структурных схем.
Для дальнейших исследований динамических свойств асинхронных ^ электродвигателей целесообразно результирующие векторы представить в виде проекций на комплексной плоскости и записать их через вещественные и мнимые части в следующем виде:

 (14)
(14)
Совместив вектор напряжения статора с действительной осью координатной системы, т. е. положив u1 =0, на основании (7) получим
 ; (15)
; (15)
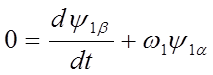 ; (16)
; (16)
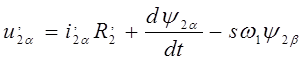 ; (17)
; (17)
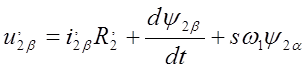 . (18)
. (18)
Выразив также электромагнитный момент по уравнению (9) через составляющие векторов тока и потокосцепления
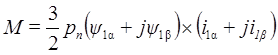
и применив правило векторного произведения векторов, получим абсолютное значение момента:
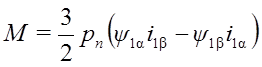 , (19a)
, (19a)
где ![]() ;
;
![]()
Воспользовавшись выражением (10), можно аналогично получить
 (19б)
(19б)
где ![]() ;
;
![]()
Составляющие тока ротора могут быть выражены через составляющие потокосцепления в следующем виде:
 (20)
(20)
где k1 - коэффициент электромагнитной связи статора;
k1 =Lm /L1 ; (21a)
![]() . (21б)
. (21б)
С учетом (8) и (21а) можно выражения моментов записать в форме, удобной для вывода передаточных функций двигателя;
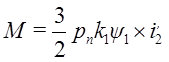
или
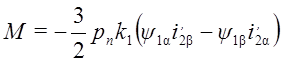 . (22)
. (22)
В случае одновременного изменения частоты и напряжения статора, при котором потокосцепление статора остается постоянным, из уравнений (15) и (16) можно получить
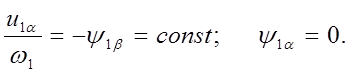 (23)
(23)
Для двигателя с короткозамкнутым ротором в уравнениях (17), (18) ![]() . Выразив из уравнений (20) 2
и 2
и подставив их в уравнения (17), (18), получим
. Выразив из уравнений (20) 2
и 2
и подставив их в уравнения (17), (18), получим
 (24)
(24)
 (25)
(25)
 . (26)
. (26)
Рассматривая переменные величины в приращениях относительно начальных значений ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , получим из (23) - (26) уравнения для статического режима, связывающие начальные значения координат,
, получим из (23) - (26) уравнения для статического режима, связывающие начальные значения координат,
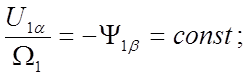 (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
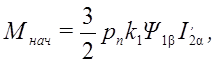 (30)
(30)
и уравнения для динамического режима, связывающие приращения координат:
 (31)
(31)
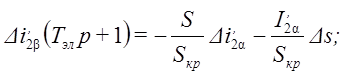 (32)
(32)
 (33)
(33)
где ![]() - электромагнитная постоянная времени электродвигателя;
- электромагнитная постоянная времени электродвигателя;
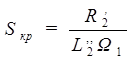 - критическое скольжение.
- критическое скольжение.
На основании уравнений (27)-(33) можно записать передаточную функцию
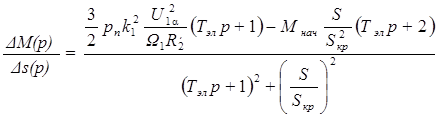 (34)
(34)
Выражение  в первом слагаемом числителя (34) представляет собой значение фиктивного пускового момента Мп.ф.
определяемое в результате линеаризации рабочей части механической характеристики двигателя для принятых значений напряжения статора U1
и угловой частоты напряжения статора 1
:
в первом слагаемом числителя (34) представляет собой значение фиктивного пускового момента Мп.ф.
определяемое в результате линеаризации рабочей части механической характеристики двигателя для принятых значений напряжения статора U1
и угловой частоты напряжения статора 1
:
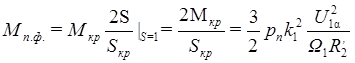 , (35)
, (35)
где 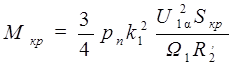 - критический момент двигателя.
- критический момент двигателя.
Момент Мнач во втором слагаемом числителя (34) можно записать с учетом принятых допущений в виде
 , (36)
, (36)
С учетом (35) и (36) выражение (34) примет следующий вид:
 . (37)
. (37)
Для рабочей части механической характеристики двигателя можно принять
![]() ,
,
и тогда передаточную функцию (37) можно записать в упрощенном виде
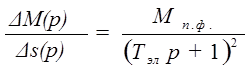 (38)
(38)
Представив зависимость скольжения электродвигателя от угловой частоты напряжения статора в приращениях и выполнив линеаризацию при условии, что в рабочей области sl, получим
 (39)
(39)
Уравнение равновесия моментов (13) может быть записано в приращениях в виде
![]() . (40)
. (40)
На основании полученных выражений может быть составлена структурная схема асинхронного двигателя при управлении угловой частотой напряжения статора и при условии постоянства потокосцепления статора. Однако это удобнее сделать, если представить координаты двигателя в о. е., приняв за базовые значения координат их значения в номинальном режиме: Мп.ф.н.
, 1н
, U1н
, 0н
=1н
/pп
где 0н
- синхронная угловая скорость двигателя. Тогда ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Передаточная функция (37) с учетом (39) запишется так:
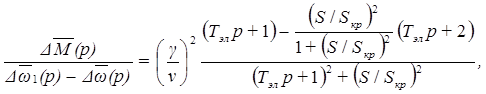 (41)
(41)
где =U1 /U1н - относительное напряжение статора; =1 /1н – относительная частота напряжения статора.
Или в упрощенном виде:
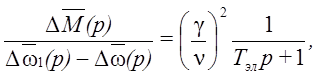 (42)
(42)
Соответственно на основании уравнения (40) имеем
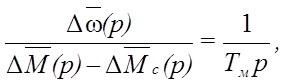 (43)
(43)
где Tм =J0н /Мп.ф.н - механическая постоянная времени двигателя.
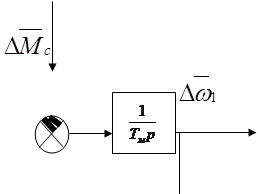
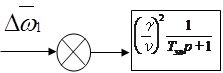
Упрощенная структурная схема асинхронного двигателя при управлении угловой частотой напряжения статора, построенная на основании выражений (42), (43), показана на рис. 1.
 |
 |
![]()
![]()
![]()
Рис.1.
Используя изложенный выше подход к выводу передаточных функций двигателя, можно получить передаточную функцию, связывающую изменение электромагнитного момента двигателя М при изменении напряжения статора u1 и неизменной частоте напряжения статора (1 =const). Этот случай соответствует изменяющемуся потокосцеплению статора. В о. е. получим
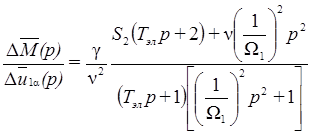 , (44)
, (44)
Где S2 - абсолютное скольжение электродвигателя в рабочей точке, равное отношению угловой частоты ЭДС ротора 2 (приведенной к двухполюсному электродвигателю) к номинальному значению угловой частоты напряжения статора 1н .
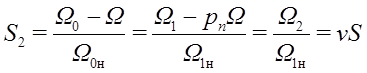 .
.
Структурная схема асинхронного электродвигателя при управлении напряжением статора показана на рис. 2.
 |
Рис.2.
2.3 Статические характеристики САУ на основе АД
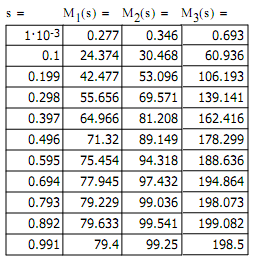
2.3.1 Статические характеристики САУ при ![]()
Для построения механических характеристик разомкнутой системы электропривода в диапазоне скоростей, меньше синхронной, воспользуемся зависимостью для момента М в функции скольжения при f=var.

Где Uф.с.м – номинальное фазное напряжения статора;
f – частота напряжения на выходе инвертора;
nc – синхронная скорость двигателя;
rp ’, xp ’, rc , xc – параметры схемы замещения двигателя;
После подсчета в программе MathCad получаем механические характеристики:

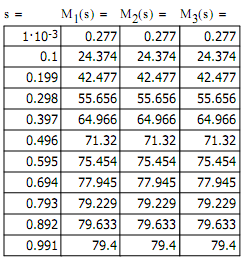
2.3.2 Статические характеристики САУ при ![]()
Для построения механических характеристик разомкнутой системы электропривода в диапазоне скоростей, меньше синхронной, воспользуемся зависимостью для момента М в функции скольжения при f=var.

После подсчета в программе MathCad получаем механические характеристики:

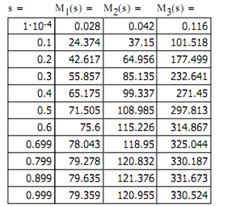
2.3.3 Статические характеристики САУ при вентиляторной нагрузке
Для построения механических характеристик разомкнутой системы электропривода в диапазоне скоростей, меньше синхронной, воспользуемся зависимостью для момента М в функции скольжения при f=var.

После подсчета в программе MathCad получаем механические характеристики:

3. Динамические характеристики САУ переменного тока
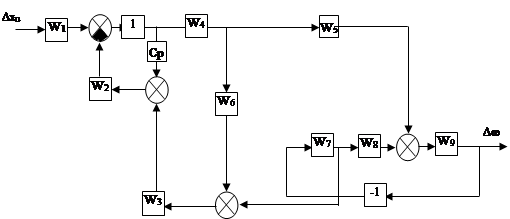
Исходная структурная схема разомкнутой САУ:
ПЧ АД
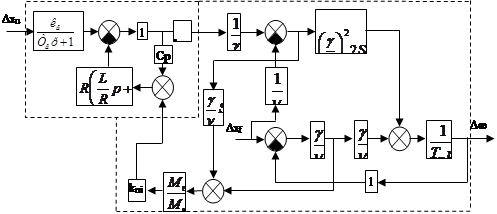 |
1 -Преобразование структурной схемы.
Получим передаточную функцию разомкнутой системы «ПЧ-АД по каналу управления напряжением:
 ; при условии
; при условии ![]()
 |
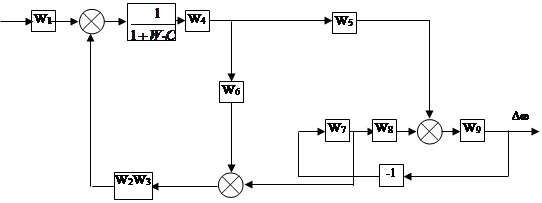
Этап первый
 |
Этап второй
|
|
 |
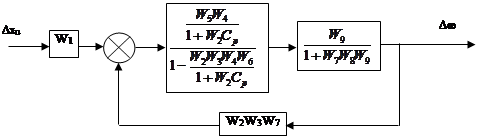
Этап третий
 |
Этап четвертый
 |
Этап пятый
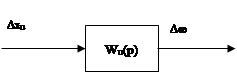 |
Получили передаточную функцию разомкнутой системы «ПЧ-АД по каналу управления напряжением
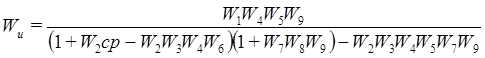
Где
 ;
;
![]() ;
;![]()
![]() ;
; 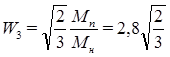 ;
; 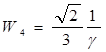 ;
;

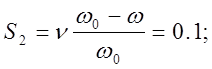
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
;![]()
Заменяем W1 ,W2 ,…,W9
Упрощаем структурную формулу
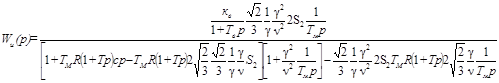
Полученная функция имеет вид:
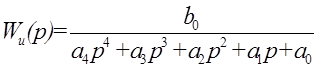
Выпишем значения коэффициентов a4 , a3 , a2 , a1 , a0 перед p4 , p3 , p2 , p1 , p0 соответственно.
![]() ;
;
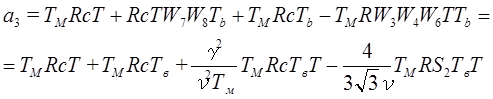 ;
;
![]()
![]()
![]()
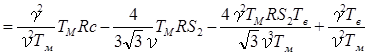
![]() ;
;
Коэффициент числителя

Рассчитаем данные коэффициенты с помощью MathCad.
Получим коэффициенты:
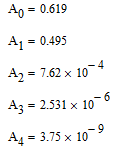
4. Анализ устойчивости САУ.
4.1 Критерий устойчивости Гурвица
![]()
![]()
Условие устойчивости.
![]()

Вывод: Исходя из критерия устойчивости Гурвица система устойчива.
4.2 Критерий устойчивости Найквиста
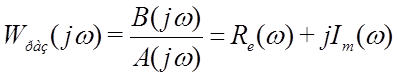
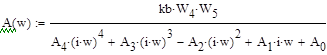
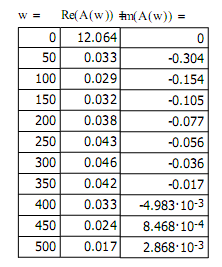

4.3 Критерий устойчивости Михайлова
![]()
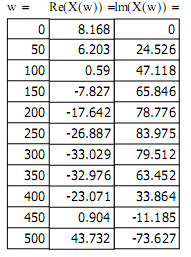

4.4 Построение логарифмических амплитудно- и фазочастотных характеристик
Формулы для расчета ЛАЧХ и ФЧХ.
![]() ;
;
![]()
![]()
![]()


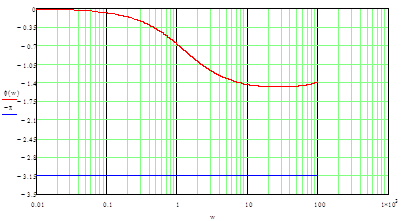
Запас по фазе равен 85,9
Частота среза равна 15 рад/с
5. Расчет переходного процесса
Для получения графика переходного процесса выполним обратное преобразование Лапласа для функции.

При значениях
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
6.Вывод
В ходе проделанной курсовой работы я получил практические навыки по построению структурной схемы для системы «Управляемый выпрямитель - автономный инвертор напряжения – асинхронный двигатель». Получил передаточную функцию. Проверил систему автоматического управления на устойчивость с помощью критериев устойчивости (Гурвица, Найквиста, Михайлова).
Построил логарифмические амплитудно- и фазо-частотные характеристики и график переходного процесса.
Список литературы
1. Комплектные электроприводы: Контрольные задания и методические указания для студентов заочного факультета специальности 21.05. / Сост. С.Н. Сидоров – Ульяновск, 1990. – 44с.
2. Управление электроприводами: Учебное пособие для вузов. – Л.: Энергоиздат. Ленингр. отд-ние, 1982. – 392 с., ил.
3. Настройка комплектного электропривода постоянного тока ЭТУ 3601: сборник лабораторных работ для студентов специальности 21.05./Сост. С.Н. Сидоров. – Ульяновск, 1992. - 28 с.