Тема 11. Адаптивная фильтрация цифровых данных пусть они постараются подчинить себе обстоятельства, а не подчиняются им сами

СОДЕРЖАНИЕ: Если в этой теории Вы не увидите смысла, тем лучше. Можно пропустить объяснения и сразу приступить к ее практическому использованию

ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ

Digital signals processing

Тема 11. АДАПТИВНАЯ ФИЛЬТРАЦИЯ ЦИФРОВЫХ ДАННЫХ

Пусть они постараются подчинить себе обстоятельства, а не подчиняются им сами.

Гораций. Послания. Римский поэт, I в.д.н.э.

Если в этой теории Вы не увидите смысла, тем лучше. Можно пропустить объяснения и сразу приступить к ее практическому использованию.

Валентин Ровинский. Теория карточных игр.

Киевский геофизик Уральской школы, ХХ в.

Содержание

Введение.

1. Общие сведения об адаптивной цифровой фильтрации . Основные области применения. Адаптивный шумоподавитель. Адаптивный фильтр Винера. Адаптивный алгоритм наименьших квадратов Уидроу-Хопфа. Рекурсивные схемы наименьших квадратов.

2. Основы статистической группировки информации. Предпосылки метода. Задача статистической группировки. Использование априорных данных. Эффективность метода.

3. Статистическая регуляризация данных. Проверка теоретических положений метода. Оценка сохранения разрешающей способности. Статистическая оценка регуляризации данных. Результаты моделирования. Частотное представление. Пример практического использования.

4. Статистическая группировка полезной информации. Сущность аппаратной реализации. Особенности аппаратной реализации. Реализация систем группировки информации. Пример исполнения системы группировки информации.

Введение

В традиционных методах обработки данных информация извлекается из входных сигналов линейными системами с постоянными параметрами алгоритмов преобразования данных. Системы могут иметь как конечную, так и бесконечную импульсную характеристику, но передаточная функция систем не зависит от параметров входных сигналов и их изменения во времени.

Адаптивные устройства обработки данных отличаются наличием определенной связи параметров передаточной функции с параметрами входных, выходных, ожидаемых, прогнозируемых и прочих дополнительных сигналов или с параметрами их статистических соотношений, что позволяет самонастраиваться на оптимальную обработку сигналов. В простейшем случае, адаптивное устройство содержит программируемый фильтр обработки данных и блок (алгоритм) адаптации, который на основании определенной программы анализа входных, выходных и прочих дополнительных данных вырабатывает сигнал управления параметрами программируемого фильтра. Импульсная характеристика адаптивных систем также может иметь как конечный, так и бесконечный характер.

Как правило, адаптивные устройства выполняются узкоцелевого функционального назначения под определенные типы сигналов. Внутренняя структура адаптивных систем и алгоритм адаптации практически полностью регламентируются функциональным назначением и определенным минимальным объемом исходной априорной информации о характере входных данных и их статистических и информационных параметрах. Это порождает многообразие подходов при разработке систем, существенно затрудняет их классификацию и разработку общих теоретических положений /л38/. Но можно отметить, что наибольшее применение при разработке систем для адаптивной обработки сигналов находят два подхода: на основе схемы наименьших квадратов (СНК) и рекурсивной схемы наименьших квадратов (РСНК).

11.1. ОБЩИЕ СВЕДЕНИЯ ОБ АДАПТИВНОЙ ЦИФРОВОЙ ФИЛЬТРАЦИИ [38, 43].

Основные области применения адаптивной фильтрации – очистка данных от нестабильных мешающих сигналов и шумов, перекрывающихся по спектру со спектром полезных сигналов, или когда полоса мешающих частот неизвестна, переменна и не может быть задана априорно для расчета параметрических фильтров. Так, например, в цифровой связи сильная активная помеха может интерферировать с полезным сигналом, а при передаче цифровой информации по каналам с плохими частотными характеристиками может наблюдаться межсимвольная интерференция цифровых кодов. Эффективное решение этих проблем возможно только адаптивными фильтрами.

Частотная характеристика адаптивных фильтров автоматически регулируется или модифицируется в соответствии с определенным критерием, позволяющем фильтру адаптироваться к изменениям характеристик входного сигнала. Они достаточно широко используются в радио- и гидролокации, в системах навигации, в выделении биомедицинских сигналов, и многих других отраслях техники. В качестве примера рассмотрим наиболее распространенные схемы адаптивной фильтрации сигналов.

Адаптивный шумоподавитель . Блок-схема фильтра приведена на рис. 11.1.1.

Рис. 11.1.1.

Фильтр состоит из блока цифрового фильтра с регулируемыми коэффициентами и адаптивного алгоритма для настройки и изменения коэффициентов фильтра. На фильтр одновременно подаются входные сигналы y(k) и x(k). Сигнал y(k) содержит полезный сигнал s(k) и некоррелированный с ним загрязняющий сигнал g(k). Сигнал x(k) какого-либо источника шума, коррелированный с g(k), который используется для формирования оценки сигнала (k). Полезный сигнал оценивается по разности:

(k) = y(k) – (k) = s(k) + g(k) – (k). (11.1.1)

Возводим уравнение в квадрат и получаем:

2 (k) = s2 (k) + (g(k) – (k))2 + 2.s(k) (g(k) – (k)). (11.1.2)

Вычислим математическое ожидание левой и правой части этого уравнения:

M[2 (k)] = M[s2 (k)] + M[(g(k) – (k))2 ] + 2M[s(k) (g(k) – (k))]. (11.1.3)

Последнее слагаемое в выражении равно нулю, поскольку сигнал s(k) не коррелирует с сигналами g(k) и (k).

M[2 (k)] = M[s2 (k)] + M[(g(k) – (k))2 ]. (11.1.4)

В этом выражении M[s2 (k)] = W(s(k)) – мощность сигнала s(k), M[2 (k)] = W((k)) – оценка мощности сигнала s(k) и общая выходная мощность, M[(g(k) – (k))2 ] = W(eg ) - остаточная мощность шума, который может содержаться в выходном сигнале. При настройке адаптивного фильтра к оптимальному положению минимизируется мощность остаточного шума, а, следовательно, и мощность выходного сигнала:

min W((k)) = W(s(k)) + min W(eg ). (11.1.5)

На мощность полезного сигнала настройка не влияет, поскольку сигнал не коррелирован с шумом. Эффект минимизации общей выходной мощности будет выражаться в максимизации выходного отношения сигнал/шум. Если настройка фильтра обеспечивает равенство (k) = g(k), то при этом (k) = s(k). Если сигнал не содержит шума, адаптивный алгоритм должен устанавливать нулевые значения всем коэффициентам цифрового фильтра.

Рис. 11.1.2.

Адаптивный фильтр Винера . Входной сигнал y(k) фильтра, приведенного на рис. 11.1.2, включает компоненту, коррелированную с со вторым сигналом x(k), и полезную компоненту, некоррелированную с x(k). Фильтр формирует из x(t) сигнал (k) - оптимальную оценку той части у(k), которая коррелированна с x(k), и вычитает ее из сигнала y(k). Выходной сигнал:

e(k) = y(k) - (k) = y(k) - H T X k = y(k) -h(n) x(k-n),

где H T и X k – векторы весовых коэффициентов фильтра и его входного сигнала.

Аналогично предыдущему методу, возводим в квадрат левую и правую части уравнения, находим математические ожидания обеих частей и получаем уравнение оптимизации e выходного сигнала:

e = s2 + 2P T H + H T RH , (11.1.6)

где s2 = M[y2 (k)] – дисперсия y(k), P = M[y(k)X k ] – вектор взаимной корреляции, R = M[X k X k T ] – автокорреляционная матрица.

Рис. 11.1.3.

В стационарной среде график зависимости e от коэффициентов H представляет собой чашеобразную поверхность адаптации (рис. 11.1.3). Градиент поверхности:

D = de / dH = -2P + 2RH .

Каждому набору коэффициентов h(n) на этой поверхности соответствует определенная точка. В точке минимума градиент равен нулю и вектор весовых коэффициентов фильтра является оптимальным:

H opt = R -1 P . (11.1.7)

Эта формула называется уравнением Винера-Хопфа. Задачей алгоритма автоматической настройки является подбор таких весовых коэффициентов фильтра, которые обеспечивают работу в оптимальной точке поверхности адаптации.

Однако практическое применение фильтра затрудняется использованием корреляционных матриц R и P, априори неизвестных, и которые могут изменяться со временем для нестационарных сигналов.

Адаптивный алгоритм наименьших квадратов Уидроу-Хопфа . По существу, это модификация фильтра Винера, в которой вместо вычисления коэффициентов (11.1.7) за один шаг используется алгоритм последовательного спуска в оптимальную точку при обработке каждой выборки:

H k +1 = H k - mek X k , (11.1.8)

ek = yk - H T X k . (11.1.9)

Условие сходимости к оптимуму:

0 m 1/lmax , (11.1.10)

где m - параметр скорости спуска, lm ax – максимальное собственное значение ковариационной матрицы данных. Блок-схема алгоритма приведена на рис. 11.1.4.

Рис. 11.1.4. Алгоритм адаптации методом наименьших квадратов.

На практике точка максимальной оптимальности флюктуирует около теоретически возможной. Если входной сигнал нестационарный, то изменение статистик сигнала должно происходить достаточно медленно, чтобы коэффициенты фильтра успевали следить за этими изменениями.

Рекурсивные схемы наименьших квадратов отличаются тем, что вычисление каждой последующей выборки коэффициентов h(n) производится не только по коэффициентам только одной предыдущей выборки, но и с определенной длиной постепенно затухающей памяти по предшествующим выборкам, что позволяет снижать флюктуации оценок при обработке стационарных сигналов.

11.2. Основы статистической группировки информации.

При построении систем адаптивной фильтрации данных большое значение имеют статистические характеристики обрабатываемых сигналов и шумов, их стационарность, и наличие какой-либо дополнительной информации, коррелированной с основной. Возможность использования дополнительной информации при построении адаптивных систем рассмотрим на конкретном примере – системе адаптивной фильтрации данных непрерывных ядерногеофизических измерений.

Предпосылки метода. Физической величиной, регистрируемой в процессе ядерно-физических измерений в геофизике, обычно является частота импульсных сигналов на выходе детекторов ионизирующего излучения в интегральном или дифференциальном режиме амплитудной селекции. Значения измеряемой величины, как статистически распределенной по своей природе, могут быть определены только путем усреднения числа актов регистрации ионизирующих частиц по интервалам времени. Зарегистрированное количество импульсов определяет статистическую погрешность единичного измерения, а временной интервал усреднения, обеспечивающий нормативную погрешность – их производительность. Для методов с непрерывной регистрацией информации во времени (или в пространстве) временное окно измерений определяет также временную (или пространственную, с учетом скорости перемещения детектора) разрешающую способность интерпретации результатов измерений, при этом эффективность регистрации информации обычно ограничена условиями измерений и/или техническими средствами их исполнения. Типичный пример - каротаж скважин, где возможности увеличения интенсивности потоков информации ограничены параметрами эффективности регистрации и чувствительности детекторов излучения, которые зависят от их типа и размеров. Размеры детекторов, естественно, существенно зависят от размеров скважинных приборов, которые, в свою очередь, ограничены диаметрами скважин.

Ниже рассматривается возможность повышения точности и производительности непрерывных ядерно-физических измерений, для наглядности, применительно к условиям измерений в варианте скважинного гамма-опробования, хотя в такой же мере она может быть использована в авто- и аэрогаммасъемке, при радиометрическом обогащении руд, в рентгенорадиометрии и других методах ядерной геофизики. Предполагается, что регистрация данных производится в цифровой форме с накоплением отсчета по постоянным интервалам дискретизации данных (по времени и по пространству, при условии постоянной скорости перемещения детектора).

В общем случае полезная (целевая) информация может присутствовать в нескольких энергетических интервалах спектра излучения. Рабочими интервалами измерений обычно счи­таются участки спектра, где полезная информация присутствует в чистом виде либо в смеси с помехами (фоном), значение которых может быть учтено при обработке результатов изме­рений. Так, например, при гамма-опробовании пород на содержание естественных радионук­лидов (ЕРН) регистрируется излучение с энергией более 250-300 кэВ, представленное в основном первичными и однократно рассеянными квантами, плотность потока которых про­порциональна массовой доле ЕРН в породах. Плотность потока излучения в низкоэнергети­ческом интервале спектра (20-250 кэВ, в основном многократно рассеянное излучение) также зависит от массовой доли ЕРН, но эта зависимость является параметрически связанной с эф­фективным атомным номером излучающе-поглощающей среды в области детектора, вариации которого по стволу скважины могут приводить к большой погрешности интерпретации ре­зультатов измерений. Между тем плотность потока информации (относительно массовой доли ЕРН) в интервале 20-250 кэВ много выше, чем в интервале более 250 кэВ, осо­бенно при регистрации излучения сцинтилляционными детекторами малых объемов, которые имеют повышенную чувствительность именно к низкоэнергетической части спектра излуче­ния.

Задача статистической группировки информации в потоках сигналов в общей и наибо­лее простой форме может быть сформулирована следующим образом. Полезная информация присутствует в двух статистически независимых потоках сигналов (в двух неперекрывающихся интервалах спектра излучения). В первом потоке сигналов, условно- основном, полезная информация присутствует в чистом виде: плотность потока сигналов пропорциональна опреде­ляемой физической величине. Во втором потоке, условно-дополнительном, на полезную ин­формацию наложено влияние дестабилизирующих факторов, значение которых неизвестно. При отсутствии дестабилизирующих факторов коэффициент корреляции средних значений плотностей потоков в этих двух потоках сигналов постоянен и близок к 1. Для снижения ста­тистической погрешности измерений требуется осуществить извлечение полезной информа­ции из дополнительного потока сигналов и ее суммирование с основным потоком.

Обозначим потоки, а равно и частоты основного и дополнительного потоков сигналов индексами n и m (импульсов в секунду), связь потоков по частотам индексом х = m/n. Определению подлежит частота потока n. Значение х может изменяться за счет влияния дестабилизирующих факторов на поток m и в общем случае представляет собой случайную величину, распределенную по определенному закону с плотностью вероятностей Р(х), мате­матическим ожиданием , и дисперсией Dx .

На основе теоремы Байеса, плотность вероятностей распределения частоты n по измеренному за единичный интервал t числу отсчетов сигнала N определяется выражением:

PN (n) = P(n) Pn (N) /P(N), (11.2.1)

Pn (N) = (nТ)N e-n t /N! , (11.2.2)

P(N) =Pn (N) P(n) dn, (11.2.3)

где: P(n) - априорная плотность вероятностей частоты n, Pn (N) - апостериорное распределе­ние вероятностей числовых отсчетов N (закон Пуассона). Принимая в дальнейшем в качестве искомой величины значения отсчетов z=nt по интервалам t (экспозиция цифровых отсчетов или скользящее временное окно аналоговых данных) и подставляя (11.2.2, 11.2.3) в (11.2.1), получаем:

PN (z) = P(z) zN e-z /P(z) zN e-z dz. (11.2.4)

При неизвестном распределении значений z априорная плотность распределения P(z) принимается равномерной от 0 до , при этом из выражения (11.2.4) следуют общеизвестные выражения:

z = Dz = N+1 @ N, (11.2.5)

dz 2 = Dz /z2 = 1 /(N+1) @ 1/N. (11.2.6)

Значениями единиц в выражениях пренебрегаем, что не только корректно в условиях хорошей статистики, но и необходимо в режиме последовательных непрерывных измерений для исключения смещения средних значений.

Как следует из теории гамма-каротажа (ГК) и достаточно хорошо подтверждено практикой гамма-опробования, пространственная разрешающая способность гамма-каротажных измерений при интерпретации результатов ГК на содержание естественных радиоактивных элементов в породах по стволу скважин в среднем составляет 10 см, а в скважинах малого диаметра может даже повышаться до 5-7 см. Однако реализация такой разрешающей способности возможна только в условиях достаточно хорошей статистики. Коэффициент усиления дисперсии помех цифровых фильтров деконволюции, которые используются при интерпретации ГК, в среднем порядка 12 и изменяется от 4 до 25 в зависимости от плотности пород, диаметра скважин, диаметра скважинных приборов и пр. Отсюда следует, что для достижения разрешающей способности в 10 см при нормативной погрешности дифференциальной интерпретации не более 10-20 % статистическая погрешность измерений не должна превышать 3-7 %. А это, в свою очередь, определяет объем отсчета за единичную экспозицию не менее 200-1000 импульсов. При гамма-каротаже последнее возможно только для пород с относительно высоким содержанием ЕРН (более 0.001 % эквивалентного урана), при использовании детекторов больших размеров (с эффективностью регистрации более 10 имп/сек на 1 мкР/час) и при низкой скорости каротажа (не более 100-300 м/час). В той или иной мере эта проблема характерна для всех методов ядерной геофизики, и особенно остро стоить в спектрометрических модификациях измерений.

Вместе с тем следует отметить, что процесс непрерывных измерений имеет определенную физическую базу как для применения методов регуляризации результатов интерпретации данных, так и для регуляризации непосредственно самих статистических данных (массивов отсчетов N) при их обработке.

Простейшим способом подготовки цифровых данных для интерпретации является их низкочастотная фильтрация методом наименьших квадратов (МНК) или весовыми функциями (Лапласа-Гаусса, Кайзера-Бесселя и др.). Однако любые методы низкочастотной фильтрации данных снижают пространственную разрешающую способность интерпретации, так как кроме снижения статистических флюктуаций приводят к определенной деформации частотных составляющих полезной части сигнала, спектр которого по условиям деконволюции должен иметь вещественные значения вплоть до частоты Найквиста. В определенной мере ликвидировать этот негативный фактор позволяет метод адаптивной регуляризации данных (АРД).

Выражения (11.2.5-6) получены в предположении полной неизвестности априорного распределения P(z) для отсчетов в каждой текущей экспозиции t. Между тем, при обработке данных непрерывных измерений, и тем более каротажных данных, которые обычно являются многопараметровыми, для каждого текущего отсчета при обработке данных может проводиться определенная оценка распределения P(z). Как минимум, можно выделить два способа оценки распределения P(z).

Способ 1. По массивам данных параллельных измерений каких-либо других информационных параметров, значения которых достаточно четко коррелированны с обрабатываемым массивом данных либо в целом по пространству измерений, либо в определенном скользящем интервале сравнения данных. К таким массивам относятся, например, предварительные каротажные измерения в процессе бурения скважин, измерения другим прибором, с другой скоростью каротажа, в другом спектральном интервале излучения, и даже другим методом каротажа. При гамма-опробовании оценка распределения P(z) может производиться по параллельным измерениям интенсивности потока m в низкочастотном интервале спектра горных пород.

Способ 2. При единичной диаграмме ГК оценка распределения P(z) в каждой текущей точке обработки данных может выполняться по ближайшим окрестностям данной точки, захватывающим более широкий пространственный интервал по сравнению с интервалом отсчетов.

Использование априорных данных. Допустим, что кроме основного массива данных N, подлежащего обработке (подготовке к интерпретации), мы располагаем дополнительным массивом данных M, значения которого в определенной степени коррелированы с массивом N. При отсутствии дополнительных массивов способ 2 позволяет получить массив М обработкой массива N цифровым фильтром МНК (или любым другим весовым фильтром) со скользящим временным окном T 3t (M(k) = m(k)t сглаженного сигнала m(k) = n(k) h, где h – оператор симметричного цифрового фильтра). Отметим также, что 2-ой способ всегда может использоваться для регуляризации данных независимо от наличия данных для 1-го метода.

Массив М позволяют дать оценку статистических характеристик распределения P(z). Так, если для тех же интервалов времени t в массиве М имеются отсчеты М = mk t (или приведенные к ним отсчеты какого-либо другого параметра), то можно записать:

PM (z) =, (11.2.7)

где Р(х) – априорная плотность распределения значений xk = mk /nk , которые в общем случае также могут быть случайными. При равномерном распределении Р(х) от 0 до для отсчета М равновероятно любое значение z, т.е. эффект от измерений в потоке m отсутствует. Однако по исходным условиям задачи в потоке m обязательно присутствие полезной информации, а, следовательно, и суще­ствование, как минимум, определенных границ распределения Р(х) от хmin 0 до xmax , и среднего значения по пространству измерений. При этом из выражения (11.2.7) следует, что наиболее вероятное значение za , априорное для отсчетов z=nt в потоке n по измерениям в потоке m (отсчетам М), должно быть равно:

za = (M+1)/ @ М/. (11.2.8)

При статистической независимости величин х и М относительная средняя квадратическая погрешность определения значений za по отсчетам в массиве М:

dza 2 = dM 2 + dx 2 . (11.2.9)

Отсюда дисперсия распределения значений za :

Dza = (DM +M2 dx 2 )/2 = D(M) /2 , (11.2.10)

D(M) = DM +M2 dx 2 = DM +Dxm , (11.2.11)

DM = М+1 @ М, Dxm = M2 dx 2 ,

где значение дисперсии DM определяется статистикой отсчетов в массиве М при х = const, значение Dxm представляет собой дисперсию значений М за счет флюктуаций величины х, а сумма D(M) определяет полную дисперсию отсчетов М.

Влияние Р(х) на форму распределения РМ (z) сказывается в его растягивании по координате z относительно модального значения, при этом решение интеграла (11.2.7) в первом приближении может быть представлено в следующем виде:

PM (z) @ be-bz . (11.2.12)

Для данного распределения:

= za = a/b, (11.2.13)

Dza = a/b2 , (11.2.14)

С учетом выражений (11.2.8) и (11.2.10):

a = MDM /(Dza 2 ) = MDM /D(M), (11.2.15)

b = DM /(Dza ) = DМ /D(M). (11.2.16)

Значение а в выражении (11.2.15) принимается целочисленным. Выражение (11.2.12) может быть принято для распределения (11.2.4) в качестве априорного распределения вероятностей Р(z), при этом:

PN (z) = (b+1) e-z(b+1) . (11.2.17)

Отсюда, математическое ожидание и дисперсия z:

z = (N+a)/(b+1), (11.2.18)

Dz = (N+a)/(b+1)2 . (11.2.19)

C использованием выражений (11.2.15-16):

z = bN+(1-b)M/, (11.2.20)

где b и (1-b) – весовые коэффициенты доверия отсчетам N и M:

b = D(M)/(DN 2 +D(M)). (11.2.21)

Дисперсия и относительная средняя квадратическая погрешность отсчетов z:

Dz = D(M), (11.2.22)

dz 2 =1/(N+MDM /D(M)). (11.2.23)

Эффективность метода. Сравнение выражений (11.2.20-23) и (11.2.5-6) позволяет дать оценку эффекта использования дополнительной информации из статистически независимого от N потока М (произвольная дополнительная информация).

1. При const имеет место dх 2 0, Dxm 0 и дисперсия отсчетов в массиве М определяется только статистикой потока:

D(M) DM = M, z = (N+M) /(+1),

dz 2 1/(N+M) dN 2 = 1/N, (11.2.24)

h = dN 2 /dz 2 = [N+M2 /D(M)] /N 1+M/N,

что соответствует определению z по двум независимым измерениям и эффект использования дополнительной информации максимален. Так, при M » N, h 2 и погрешность измерений уменьшается в ~1.4 раза.

2. В общем случае Dxm 0, при этом D(M) DМ и положительный эффект снижается. В пределе: dx , Dxm , D(M) , h 1, z N, dz dN и положительный эффект полностью вырождается. Во всех остальных случаях h 1 и dz dN . Отсюда следует, что при наличии коррелированной информации в массиве М положительный эффект, в той или иной мере, всегда имеет место.

3. Положительный эффект тем больше, чем больше значение x = m/n, меньше флюктуации х (величина dх ), и меньше значения отсчетов N = nt. Положительный эффект увеличивается именно в тех случаях, когда особенно остро ощущается недостаток информации: при малых значениях плотности потока излучения и/или экспозиции измерений.

Аналогичный эффект будет иметь место и при формировании отсчетов M по окрестностям текущих точек обработки данных путем определения их среднего значения (низкочастотное сглаживание массива n). Предварительное низкочастотное сглаживание может применяться и для статистически независимого дополнительного массива m, что будет повышать достоверность прогнозных отсчетов и увеличивать глубину регуляризации, если это сглаживание при регуляризации по формулам (11.2.20 и 21) не сказывается на изменении формы основного сигнала. Последнее определяется соотношением частотных спектров основного сигнала и оператора сглаживания.

Возможны два способа реализации уравнения (11.2.20): непосредственно в процессе измерений методом статистической группировки полезной информации (СГПИ) в реальном масштабе времени, или методом статистической регуляризации данных (СРД), зарегистрированных в виде временного (пространственного) распределения в параллельных массивах отсчетов.

11.3. Статистическая регуляризация данных.

Как следует из выражения (11.2.21), для практического использования информации из дополнительных потоков данных необходимо установить значения и диспер­сию D(M), причем, исходя из задания последней по выражению (11.2.11), должно быть известно значение dx - относительной средней квадратической флюктуации вели­чины х.

Применительно к СРД определение значений и dx по зарегистрированным мас­сивам данных не представляет затруднений как в целом по пространству измерений, так и в виде распределений в скользящем окне усреднения данных. Последнее эквивалентно приведе­нию Dxm = 0 для текущей точки обработки данных по информации ее ближайших окрестно­стей и позволяет производить максимальное извлечение полезной информации из дополни­тельных потоков сигналов, если частотный спектр распределения величины х по пространству измерений много меньше частотного спектра полезного сигнала. Отметим, что информация о распределении х также может иметь практическое значение (в частности, при гамма-опробовании с дополнительным потоком сигналов в низкоэнергетическом диапазоне спектра излучения - для оценки эффективного атомного номера горных пород).

Проверка теоретических положений метода АРД проводилась путем статистического моделирования соответствующих массивов данных и их обработки цифровыми фильтрами.

В таблице 1 приведены 4 группы результатов обработки по формулам (11.2.20-21) двух статистически независимых и постоянных по средним значениям массивов данных n и m (модели постоянных полей) при различных установках СРД по скользящему окну Кс счета текущих значений = mi /ni и Di (М) по массиву m. Текущая точка обработки данных – по центру окна. Количество отсчетов в каждом массиве – 1000, распределение значений отсчетов соответствует закону Пуассона. Определение прогнозных отсчетов Мi по массиву m для использования в уравнении (11.2.20) проводилось со сглаживанием отсчетов в скользящем окне Ks низкочастотного цифрового фильтра (вариант без сглаживания при Ks = 1). В качестве низкочастотного фильтра в алгоритме СРД используется (здесь и в дальнейшем) весовое окно Лапласа-Гаусса. Теоретическое значение Dz.т. дисперсии результатов z определялось по выражению (11.2.22) с расчетом дисперсии D(M) по выражению D(M) =[1+(1/(Kc )+1/(Kc ))]. При сглаживании прогнозных отсчетов значение DM в выражении (11.2.22) принималось равным DM . = Hs , где Hs – коэффициент усиления сглаживающим фильтром дисперсии шумов (сумма квадратов коэффициентов цифрового фильтра). Дополнительно в таблице приводятся зарегистрированные средние значения коэффициента снижения статистических флюктуаций h = dn 2 /dz 2 .

Таблица 1. Статистика результатов моделирования СРД.

(Основной массив = 9.9, Dn = 9.7, дополнительный массив = 9.9, Dm = 9.9, 1000 отсчетов.)

Kc

Ks

z

Dz

Dz.т.

h

Kc

Ks

z

Dz

Dz.т.

h

3

1

9,7

5,7

6,19

1,7

11

3

9,6

3,6

3,80

2,8

5

1

9,7

5,4

5,78

1,8

11

5

9,6

3,3

3,55

3,0

11

1

9,6

5,1

5,36

1,9

11

11

9,6

3,1

3,22

3,2

21

1

9,6

5,0

5,18

2,0

11

21

9,6

3,0

3,11

3,3

51

1

9,6

5,0

5,05

2,0

11

51

9,6

3,0

2,99

3,3

3

3

9,7

4,1

4,71

2,4

3

11

9,8

4,5

4,26

2,2

5

5

9,7

3,6

4,01

2,8

5

11

9,7

3,5

3,78

2,8

11

11

9,6

3,1

3,22

3,2

11

11

9,6

3,1

3,22

3,2

21

21

9,6

2,9

2,91

3,4

21

11

9,6

3,1

3,12

3,2

51

51

9,6

2,7

2,66

3,7

51

11

9,6

3,1

2,99

3,2

Как видно из данных таблицы, практические результаты фильтрации достаточно хорошо совпадают с ожидаемыми по данным теоретических расчетов. Некоторое уменьшение среднего значения z по отношению к исходному среднему значению n определяется асимметричностью пуассоновского типа модели. При малых средних значениях модельных отсчетов в массиве m это приводит к определенной статистической асимметрии в работе СРД, т.к. при (+sm )2 (-sm )2 среднестатистическое доверие к дополнительной информации с отсчетами Mi +s меньше, чем с отсчетами Mi -s. Этим же фактором, по-видимому, вызвано и большее расхождение между теоретическими и фактическими значениями Dz при малых значениях окна Кс . Можно также заметить, что по значению коэффициента h фильтрация выходит на теоретические значения ( 1+M/N) только при достаточно точном определении значений и Di (М), что требует увеличения окна Кс счета этих параметров для полного использования дополнительной информации.

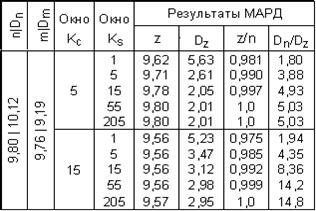
Таблица 2.

Эффект использования дополнительной информации, в полном соответствии с выражением (11.2.22), усиливается при предварительном сглаживании статистических вариаций отсчетов Mi и при увеличении значений отсчетов дополнительного массива (материалы по последнему случаю не приводятся, т.к. не имеют какой-либо дополнительной информации). В спокойных по динамике полях еще большая глубина регуляризации может быть достигнута при счете значений и Dm по сглаженному массиву М, что позволяет повысить вес прогнозных отсчетов Mi . Результаты моделирования данного варианта в тех же условиях, что и для таблицы 1, приведены в таблице 2. Такой же эффект, в принципе, может достигаться и непосредственным введением дополнительного коэффициента веса в выражение (11.2.20) в качестве множителя для значения D(M), что позволяет осуществлять внешнее управление глубиной регуляризации.

Оценка сохранения разрешающей способности полезной информации была проведена на фильтрации детерминированных сигналов n и m предельной формы – в виде прямоугольных импульсов. Оценивались два фактора: сохранение формы полезного сигнала и подавление статистических шумов, наложенных на полезный сигнал.

При установке СРД без усреднения данных по массиву М (Кs = 1, прогноз Мi по текущим значениям массива М) при любых значениях окна Кс выходной массив Z без всяких изменений повторяет массив N, т.е. не изменяет полезный сигнал и полностью сохраняет его частотные характеристики. Естественно, при условии, что массив М пропорционален массиву N.

При Кs 1 форма выходных кривых несколько изменяется и приведена на рис. 11.3.1. В индексах выходных кривых z приведена информация по установкам окон СРД: первая цифра - окно счета дисперсии DM и текущего значения (в количестве точек отсчетов), вторая цифра (через флеш) - окно сглаживания отсчетов М весовой функцией Лапласа-Гаусса и определения прогнозных отсчетов Мi . Для сравнения с результатами типовой низкочастотной фильтрации на рисунке приведена кривая n25 отсчетов N, сглаженных весовой функцией Лапласа-Гаусса с окном 25 точек.

Рис. 11.3.1. СРД прямоугольного импульса. Счет Dm по несглаженному массиву М.

На рис. 11.3.1а приведен результат СРД прямоугольного импульса с амплитудным значением 10 на фоне 5 при отношении m/n = 1 (равные значения отсчетов N и М). Дисперсия DN в выражении (11.2.21) принималась равной значению отсчетов N (статистика Пуассона). Как видно на рисунке, при сохранении фронтов сигнальной функции сглаживание прогнозных значений Мi приводит к появлению искажения формы сигнала по обеим сторонам скачка, интервал которого тем больше, чем больше значение Ks . Амплитудное значение искажений, как это и следует из выражения (11.2.21), в первую очередь зависит от соотношения текущих значений DN и D(M) и в меньшей степени от глубины сглаживания прогнозных отсчетов.

Максимальную величину искажения для точек скачка в первом приближении можно оценить из следующих соображений. Значения D(M) между точками скачка равны D(M) = А2 /4, где А - амплитуда скачка, при этом значения коэффициента b для нижней и верхней точек скачка определяются выражениями b » А2 /(4DN +A2 ), где DN = N точки скачка (для статистики Пуассона). Отсюда, при прогнозном значении М » N+А/2 для нижней точки скачка и M » N-A/2 для верхней точки относительная величина изменений N определится выражением d » 1/(2N/A+A), т.е. будет тем меньше, чем больше значения А и N и больше отношение N/A, что можно наглядно видеть на рис. 11.3.1в. Из этого выражения также следует, что максимальные искажения скачков, вносимые системой СРД, будут всегда в несколько раз меньше, чем статистические флюктуации непосредственных отсчетов d = 1/на краях скачков.

При увеличении глубины регуляризации введением счета дисперсии D(M) по сглаженному массиву М картина искажений несколько изменяется и приведена на рис. 11.3.2. Реакция СРД на сглаживание дисперсии D(M) проявляется в своеобразной компенсации абсолютных отклонений отсчетов непосредственно по сторонам скачка отклонениями противоположного знака в более дальней зоне от скачка. Максимальные значения искажений остаются примерно на таком же уровне, как и для работы по несглаженной дисперсии D(M), с несколько меньшей зависимостью от увеличения значений N и А.

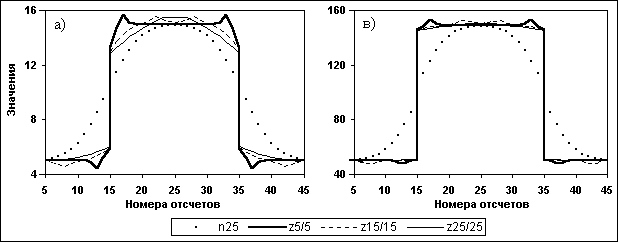
Рис. 11.3.2. СРД прямоугольного импульса. Счет Dm по сглаженному массиву М.

В приведенных примерах значение окна счета Кс принималось равным значению окна сглаживания Кs дополнительного массива М. При Кс Ks картина процесса практически не изменяется. При обратном соотношении размеров окон вступает в действие второй фактор - отклонение от фактических значений счета текущих значений xi = m/n в малом окне Кс по массиву отсчетов, сглаженных с большим окном Ks . На расстояниях от скачка функции, больших Кс /2, СРД переходит в режим предпочтения сглаженных значений массива М, т.к. D(M) 0, что при Кс Ks может приводить к появлению существенной погрешности – выбросов на расстояниях ± Кс /2 от скачков. Естественно, что при практических измерениях таких условий наблюдаться не будет и эффект резко уменьшится, но для полного его исключения вариант Kc Ks можно считать предпочтительным.

Рис. 11.3.3. СРД сигнала N по массиву M. Рис. 11.3.4. Коэффициент b.

(Счет Dm по несглаженному массиву М). (Среднее статистическое по 50 циклам)

На рис. 11.3.3 приведен пример регистрации рандомизированного модельного сигнала в виде прямоугольного импульса амплитудой 40 на фоне 10, на котором виден принцип работы СРД. Как и следовало ожидать, СРД производит сглаживание статистических флюктуаций фона и сигнала за пределами зоны ±Кс от скачка, отдавая предпочтение сглаженным прогнозным значениям Мi , и не изменяет значения фона и сигнала в пределах этой зоны в связи с резким возрастанием текущих значений D(M) в выражении (11.3.21). Изменение коэффициента b в зоне скачка, управляющего формированием выходных отсчетов, приведено на рис. 11.3.4 (среднестатистическое по 50-ти циклам рандомизации для модельного импульса на рис. 11.3.3) и наглядно показывает принцип адаптации СРД к динамике изменения значений обрабатываемых сигналов.

Статистическая оценка регуляризации данных по прямоугольным импульсам проводилась по 50-ти циклам рандомизации исходных массивов N и M. В качестве примера на рисунках 11.3.5 и 6 приведены результаты обработки статистики массивов N и Z. Кроме статистики циклов рандомизации проводилась суммарная обработка всех циклов по общей статистике фона и вершины импульсов. Результаты обработки для тех же установок фильтров приведены в таблице 3.

Рис. 11.3.5. Статистика сигнала N Рис. 11.3.6. Статистика сигнала Z

(Измерения по 50-ти циклам). (50 циклов. Счет Dm по несглаженному М)

Таблица 3.

Статистика значений фона и вершины импульсов (50 циклов).

Массивы и условия обработки

Фон

Сигнал

Сред. отсчет

Дисперсия

Сред. отсчет

Дисперсия

Основной входной массив N

Дополнительный входной массив М

Массив Z, счет Dm по несглаженному М

Массив Z, счет Dm по сглаженному М

Массив N, сглаженный весовым окном

9.96

9,89

9,87

9,84

11,5

9.97

9,49

5,47

4,76

17,9

50,1

50,2

49,7

49,9

48,5

52,0

47,4

22,3

18,6

29,2

Результаты моделирования подтверждают преимущество СРД перед простыми методами сглаживания. В числовой форме это наглядно проявляется в снижении дисперсии отсчетов выходного массива Z при практическом сохранении средних значений массива N и для фоновых отсчетов, и для амплитудных значений сигнала. При простом сглаживании развал фронтов сигнала (подавление высокочастотных составляющих спектра сигнала), как и должно быть при использовании низкочастотных фильтров, вызывает снижение по отношению к исходному массиву средних значений в максимумах и повышение фоновых значений сигнала, которое тем больше, чем больше окно весовой функции. Этот эффект особенно отчетливо проявляется в интервале окна фильтра по обе стороны от резких изменений сигнала.

При отсутствии дополнительных массивов М, коррелированных с регуляризируемым массивом N, формирование прогнозных значений Мi может производиться по ближайшим окрестностям текущих значений Ni в скользящем окне Ks . При строго корректном подходе текущая точка Ni не должна включаться в число счета прогнозных значений Mi , но, как показало моделирование, это практически не влияет на результаты регуляризации. При прогнозировании Mi по всем точкам окна Ks массив М формируется любым методом сглаживания из массива N, и все особенности работы СРД по сглаженным массивам М, рассмотренные выше, остаются без изменений при условии счета значений Dm в окне Кс по массиву М. Для исключения выбросов по обе стороны от скачков полезного сигнала счет Dm как дисперсии прогнозных значений Mi необходимо выполнять непосредственно по массиву N.

Фундаментальной особенностью СРД является возможность последовательной многократной фильтрации данных, при которой может осуществляться преимущественное повышение степени регуляризации данных с минимальными искажениями формы полезного сигнала. Для выполнения последнего размер окна Кс счета xi и Dm устанавливается минимальным (3-5 точек), а глубина регуляризации данных (степень подавления шумов) устанавливается количеством последовательных операций фильтрации (до 3-5 проходов). Пример регуляризации модельного массива N в три прохода приведен на рис. 11.3.7.

Рис. 11.3.7. СРД одиночного массива N (3 прохода. Счет Dm по массиву n)

Для сравнения пунктиром на рисунке приведено сглаживание массива 5-ти точечным фильтром Лапласа-Гаусса, который имеет коэффициент подавления шумов, эквивалентный 3-х проходному СРД (см. рис. 11.3.9).

На рисунках 11.3.8 и 11.3.9 приведены результаты статистической обработки 3-х проходной СРД для 25 циклов моделирования в сравнении с 1-м проходом и с 5-ти точечным фильтром Лапласа-Гаусса (кривая n5).

Рис. 11.3.8. Статистика средних значений Рис. 11.3.9. Статистика дисперсий

(25 циклов. Счет Dm по массиву n) (25 циклов. Счет Dm по массиву n)

Количество проходов может ограничиваться в автоматическом режиме, например, по среднеквадратическому значению корректирующих отсчетов Dzi = Ni - zi в каждом проходе по сравнению с предыдущим проходом, которое сначала резко уменьшается за счет сглаживания флюктуаций, а затем, в зависимости от динамики сигнальной функции, стабилизируется или даже начинает увеличиваться за счет искажения самого сигнала.

Частотное представление работы СРД хорошо видно на рис. 11.3.10, где приведены модули спектров рандомизированного сигнала в виде меандра (средние значения в минимуме - 20, в максимуме - 100, 25 периодов по 40 отсчетов, всего 1000 отсчетов) и результатов его обработки СРД (окно Кс = 3, окно Кs = 3).

Рис. 11.3.10. Модули спектров модельных сигналов. Рис.11.3.11. Участок спектра.

(1– входной массив N, 2– выходной массив Z, один цикл CРД,

3– выходной массив Z, три цикла CРД), 4 – массив нерандомизированного меандра).

Модуль спектра основного полезного сигнала (в данном случае чистого меандра) представляет собой последовательность отдельных частотных гармоник по всему диапазону спектра. В спектре рандомизированного меандра эти частотные гармоники суммируются со спектром шума, статистически равномерно распределенным по всему частотному диапазону (спектр шума на рисунке для наглядности сглажен). СРД осуществляет подавление шумовых составляющих сигнала, практически не затрагивая частотных гармоник меандра и не изменяя их по амплитуде. Последнее можно видеть на рис. 11.3.11, где представлен отрезок спектра сигналов в высокочастотной части главного диапазона в области одной гармоники меандра (частотные составляющие шума не сглажены). При 3-х цикловом СРД высокочастотные составляющие шумов подавляются практически на порядок.

Пример практического использования СРД приведен на рис. 11.3.12 при опробовании участка скважины, пересекающей пласты каменной соли, на содержание сильвинита по гамма-излучению Калия-40. По данным геологического опробования пласты сильвинита в толще вмещающих пород (галита) имеют достаточно резкие границы и однородны по содержанию сильвинита в пределах пластов. Исходная диаграмма ГК (детектор CsJ(Tl) со свинцовым фильтром толщиной 2 мм) и результаты фильтрации исходного массива данных ГК с использованием СРД и низкочастотного фильтра с весовым окном Лапласа-Гаусса приведены на рис. 11.3.12.

Рис. 11.3.12. Диаграммы ГК.

Результаты интерпретации диаграмм ГК симметричным деконволюционным цифровым фильтром (окно 13 точек) приведены на рис. 11.3.13. Как видно на рисунке, деконволюция по несглаженной диаграмме ГК дает существенные вариации содержания сильвинита в пределах пластов. Применение низкочастотной фильтрации диаграммы ГК снимает флюктуации содержания в пределах пластов, но существенно сглаживает границы пластов. Использование СРД позволяет устранить этот недостаток.

Рис. 11.3.13. Результаты интерпретации диаграмм ГК.

В заключение отметим, что СРД может использоваться для регуляризации не только ядернофизических данных, но и любых других числовых массивов непрерывных измерений, если радиус их корреляции не менее 3-5 отсчетов. В качестве примера на рис. 11.3.14 приведена диаграмма акустического каротажа, зарегистрированная с шагом дискретизации данных 20 см, сглаживание которой проведено СРД без потери пространственного разрешения.

Рис. 11.3.14. Диаграмма акустического каротажа и результат ее обработки СРД

(5 циклов, Kc = Ks = 3, физическое окно 0.6 м).

Курсовая работа 17-07. Модернизация адаптивного фильтра сглаживания данных, статистических распределенных по закону Пуассона.

11.3. Статистическая группировка полезной информации.

Что касается аппаратных способов реализации СГПИ, то он может быть выполнен в реальном масштабе времени, если информация представлена потоком импульсов и основным информативным параметром является скорость следования импульсов.

Сущность аппаратной реализации заключается в статистической (близкой к статистической) нормированной выборке импульсов из дополнительного потока m и их суммировании с основным потоком n с заданием условий выборки по отношению частоты следования импульсов в потоках. Пола­гая для непрерывного режима измерений M+1 = М, перепишем выражение (5.2.20) с подстановкой значения b в следующем виде:

z = N + (M/-N)·M/(M+D(M)). (11.3.1)

Умножим левую и правую части выражения на нормировочный коэффициент размножения выходного потока K = l+R:

Z = K·z= N + RN+(M/-N)·KM/(M+D(M). (11.3.2)

Заменим отсчеты RN выборкой сигналов из потока m:

RN = Рв М, (11.3.3)

где Рв - вероятность выборки сигналов из потока m. Если вероятность выборки сигналов под­держивать равной значению

Pв = R/, (11.3.4)

то при этом будет иметь место

M/-N = Рв M/R-N ® 0, (11.3.5)

и соответственно для выражения (11.3.2) имеем:

(M/-N)·KM/(M+D(M) ® 0, (11.3.6)

Z = N+Pв M ® N+RN. (11.3.7)

При статистической независимости величины х от частоты потоков n и m приведен­ные выражения действительны при определении значения как в целом по пространству измерений, так и для скользящих окон текущих значений по определенным интервалам предшествующих измерений. Действительно и обратное заключение: если по определенному интервалу измере­ний выражение (11.3.5) обращается в нуль, то установленная вероятность выборки соответствует условию (11.3.4). На этом принципе может проводиться аппаратная реализация СГПИ с авто­матической адаптацией к условиям измерений: управление процессом выборки импульсов из потока m и направление их на суммирование с потоком n по сигналам обратной связи с уст­ройства, следящего за обращением в нуль выражения (11.3.5).

Особенности аппаратной реализации СГПИ с автоматической адаптацией под условия измерений заключаются в следующем.

Значение вероятности выборки Рв не может быть больше 1. Отсюда из (11.3.3) следует, что для любых интервалов измерений должно выполняться условие М RN, а соответственно по всему пространству измерений должно выполняться условие R, чем и обуславливается выбор коэффициента R. Значение коэффициента R принципиально ограничивает степень положительного эффекта СГПИ (kmax ® 1+R), в отличие от СРД, где такого ограничения не имеется.

Относительная статистическая погрешность измерений выходного потока отсчетов Z соответ­ствует выражению (11.2.23) при условии постоянного значения величины Рв , т.е. при установке значения Рв по среднему значению величины в целом по пространству измерений. При автоматической адаптации под условия измерений значение вероятности Рв по текущему среднему значению отношения n/m определенного предшествующего интервала измерений также является статистически флюктуирующей величиной с дисперсией распределения (без учета изменений действительного значения х):

Dp = R2 (n+m)n/(m3 T), (11.3.8)

где Т- интервал усреднения информации при определении текущего значения . Соответственно, дисперсия и средняя квадратическая погрешность текущих отсчетов Z:

Dz = DN + Pв DM +M2 Dp = N+Рв М+М2 Dр , (11.3.9)

dz 2 = (N+Рв М+М2 Dр )/(N+Рв М)2 . (11.3.10)

При постоянной экспозиции измерений t положительный эффект возрастает с увеличением значения Т:

k = K2 /(K+R2 (n+m)t/mT). (11.3.11)

kmax ® 1+R, dz 2 ® 1/(N+Рв М) при Т ® . (11.3.12)

В общем случае, с учетом средней квадратической ошибки прогнозирования dxi значе­ний xi для текущих точек измерений по значениям в предшествующих интервалах при Т t:

Dz = N+Рв М+M2 (Dp +Pв 2 dxi 2 ). (11.3.13)

Формирование значения Рв на основе информации по средним значениям интер­валов измерений, предшествующих текущим, определяет СГПИ как динамическую систему с соответствующей постоянной времени реакции на изменение условий измерений. Учитывая, что, во-первых, для любой точки пространства измерений должно выполняться условие m nR, и, во-вторых, увеличение интервала Т приводит к возрастанию времени реакции на из­менение условий измерений, значение Т целесообразно ограничивать величиной порядка (5-10) значений текущих экспозиций. Чем меньше пространственная частота рас­пределения х по отношению к распределению n, тем большее значение Т допустимо.

Реализация систем СГПИ значительно облегчается при чисто практическом ограниче­нии целевой задачи: получение максимального положительного эффекта в экстремально небла­гоприятных условиях производства измерений (при низких значениях регистрируемой плот­ности потока излучения, при высокой скорости измерений) с вырождением положительного эффекта по мере снижения статистической погрешности измерений в основном потоке. Так, например, если при скважинном гамма-опробовании статистическая погрешность измерений основного потока сигналов в зонах с повышенной интенсивностью излучения снижается до 2-3%, то ее дальнейшее уменьшение не имеет практического смысла, т.к. основная погрешность каротажной радиометрической аппаратуры обычно не превышает 5%.

Использование данного целевого ограничения позволяет применить формирование параметра Рв не в скользящем окне временного или пространственного усреднения информа­ции, а по определенному зарегистрированному объему предшествующей информации, т.е. с автоматической вариацией интервала усреднения информации и постоянной регулирования Pв в зависимости от частоты потоков сигналов, при этом объем информации формирования Pв может задаваться с учетом характера вариаций величины и допустимого значения ди­намической погрешности измерений.

Для реализации такой возможности преобразуем выражение (11.3.5) по интервалу усред­нения t к виду:

Pв mt/R-nt+Q = q, (11.3.14)

Pв = nR/m = q/m, (11.3.15)

q ® Q при t ® ,

где Q- средний уровень смещения числового эквивалента сигнала обратной связи системы АРВ - автоматического регулирования вероятности выборки Рв , при котором обеспечивается вы­полнение равенства (11.3.15), m- коэффициент пропорциональности преобразования цифрового сигнала АРВ в сигнал Рв . Дифференциальное уравнение для системы АРВ:

dq/dt = n-mq/mR. (11.3.16)

Решение дифференциального уравнения при начальных условиях t = 0 и q = О (переходная функция АРВ):

q = mR(n/m) [l-exp(-mt/mR)]. (11.3.17)

Pв = R(n/m) [l- exp(-mt/mR)] = R(n/m) [1- exp(-nt/q)]. (11.3.18)

Как видно из этих выражений, значение сигнала обратной связи АРВ пропорционально отношению (n/m) частот потоков, а постоянная времени АРВ mR/m прямо пропорцио­нальна значению коэффициента преобразования m при обратной пропорциональности от зна­чения частоты дополнительного потока m, равно как и, с учетом (11.3.15), прямо пропорциональ­на текущему значению сигнала обратной связи q при обратной пропорциональности от зна­чения частоты основного потока n. Первое полностью эквивалентно второму при (n/m) ® const и q = mRn/m ® Q. В первом приближении, с использованием выражения (11.3.8) и экви­валентности значения статистических флюктуаций при Т2t для скользящего прямоугольного временного окна и окна интенсиметра с экспоненциальной переходной функцией, для отно­сительных флюктуации значения Рв получаем:

dр 2 = (n+m)/(2mRn)= (n+m)/(2qm). (11.3.19)

Выражение действительно для прямого измерения 2t-интенсиметром отношения (n/m) и является максимальной оценкой. Для более точной оценки следует учитывать, что в данном случае интенсиметр является устройством с отрицательной обратной связью по цепи АРВ, что несколько уменьшает значение флюктуации. Точная оценка может быть проведена с использованием формулы Кэмпбелла для дисперсии случайной величины x(t), образованной сложением импульсов пуассоновского потока [5], раздельно для потока n при m = const и потока m при n = const, с последующим сложением квадратов относительного среднего квадратического значения флюктуации. Так, для схемы, приведенной ниже, получено значение dр 2 (R+1)m/(2mnR2 ).

При выбранном для пространства измерений значении коэффициента R (m/n)min с использованием выражения (11.3.19) параметры системы АРВ (коэффициент m и среднее значе­ние Q для средней по пространству величины отношения n/m) могут устанавливаться под заданное значение допустимых флюктуаций вероятности выборки импульсов Рв :

m (l+(m/n)max )/(2Rdp 2 ). (11.3.20)

В процессе измерений АРВ осуществляет непрерывную адаптацию под текущие усло­вия измерений (nt ® q, mt ® mR, Pв ® q/m) с регулированием текущего значения Pв по объему информации q = (n/m)mR = nt предшествующего интервала измерений путем соответ­ствующего изменения постоянной времени интегрирования этой информации в зависимости от изменения частот потоков сигналов. При n/m ® const последнее имеет абсолютный ха­рактер: dр ® const, t ® (l/n + l/m)/(2dp 2 ).

Следует отметить, что во многих методах геофизики существуют достаточно благоприятные условия использования как СГПИ, так и СРД. Так, например, применительно к скважинному гамма-опробованию с извлечением дополнительной информации из низкоэнергетической час­ти спектра излучения условия достаточно точной реакции на изменения параметра по стволу сква­жины являются весьма хорошими, т.к. основной фактор вариации значений x - эф­фективный атомный номер среды, изменяется в небольшом диапазоне с низкой простран­ственной частотой вариаций, причем в зонах расположения активных пород, где требуется наиболее высокая точность интерпретации результатов измерений и возможны значительные изменения атомного номера пород, за счет увеличения плотностей потоков излучения посто­янная времени АРВ будет существенно уменьшаться, а пространственная разрешающая спо­собность измерений соответственно увеличиваться. Аналогичные условия характерны, как пра­вило, и для других методов ядерной геофизики.

Пример исполнения системы СГПИ для двух импульсных потоков сигналов приведен на рис. 11.3.1. Функциональная схема СГПИ содержит реверсивный счетчик импульсов 1, на вход суммирования которого подаются импульсы основ­ного потока n, а на вход вычитания - импульсы дополнительного потока m, предварительно проходящие через схему выборки импульсов 3 и счетчик-делитель частоты следования импуль­сов 4 с коэффициентом пересчета R.

Рис. 11.3.1. Базовая функциональная схема СГПИ.

1- реверсивный счетчик импульсов, 2- блок формирования сигнала выборки импульсов, 3- схема выборки импульсов, 4- счетчик-делитель частоты на R, 5- блок суммирования потоков импульсов.

Информация о состоянии счетчика 1 (сигнал q) с выходов счетчика подается на блок формирования сигнала выборки импульсов 3. В простейшем случае этот блок может представлять собой пороговое устройство (по коду числа Q), открывающее схему 3, однако выборка в этом случае имеет характер, близкий к статистическому, только при достаточно малых различиях частоты потоков n и m/R (порядка nm/R1.5n). По мере роста отноше­ния m/n независимость выборки от импульсов потока n в такой схеме вырождается, и требу­ются дополнительные устройства адаптации под текущие условия измерений. В общем случае блок 3 выполняется в виде пересчетной схемы с регулируемым коэффициентом пе­ресчета импульсов потока m в интервале 0Рв 1 по значению кода q с выхода счетчика 1 (например, с использованием статистических пересчетных схем, выполненных в виде генера­тора случайных кодов со схемой формирования сигнала выборки очередного импульса из по­тока m путем сравнения на больше-меньше текущих кодов с выхода счетчика 1 и с выхода генератора кодов).

Импульсы основного потока n и импульсы выборки из потока m, частота которых равна Рв m = R·n, поступают на вход блока 5 суммирования потоков сигналов. Интенсивность потока импульсов на выходе блока 5 равна z = n+Рв m = (1+R)n. Блок 5 может содержать пе­ресчетную схему с коэффициентом K=(1+R), при этом выходной поток будет приводиться к масштабу основного потока n и появляется возможность синхронного переключения коэффи­циентов пересчета схем 4 и 5 под различные условия измерений, при этом установка опти­мального значения коэффициента R может быть переведена в режим автоматической с управ­лением по текущему значению (в определенном интервале) информационного кода схемы 1. Альтернативное решение - подача на вход суммирования схемы 5 потока импульсов с выхода схемы 4, при этом частота потока z будет всегда в 2 раза больше потока n.

Попутно отметим, что при выводе информации q = mR(n/m) в цифровом коде со счет­чика 1 данная схема может выполнять функции универсального цифрового интенсиметра: средней частоты импульсов (n-var, m-const от генератора тактовой частоты), среднего вре­менного интервала между импульсами (m-var, n-const) и отношения частот n/m двух статис­тически распределенных потоков импульсов.

литература

38. Адаптивные фильтры. /Под ред. К.Ф.Н.Коуэна и П.М.Гранта. – М.: Мир, 1988, 392 с.

43. Айфичер Э., Джервис Б. Цифровая обработка сигналов. Практический подход. / М., Вильямс, 2004, 992 с.

Cайт автора Лекции Практикум

О замеченных ошибках и предложениях по дополнению: davpro@yandex.ru.

Copyright ©2008 Davydov А.V.

Скачать архив с текстом документа