Теорема Дирихле

СОДЕРЖАНИЕ: Содержание 1.1 Определение характера. Основные свойства характеров 3 1.2 Суммы характеров. Соотношение ортогональности 6 1.3 Характеры Дирихле 8 Введение

Содержание

Введение. 2

1. Характеры.. 3

1.1 Определение характера. Основные свойства характеров. 3

1.2 Суммы характеров. Соотношение ортогональности. 6

1.3 Характеры Дирихле. 8

2. L-функция Дирихле. 13

3. Доказательство теоремы Дирихле. 29

Введение

Простые числа расположены в натуральном ряде весьма неравномерно.

Целью данной работы является доказательство следующей теоремы о простых числах в арифметической прогрессии.

Теорема Дирихле. Если разность и первый член арифметической прогрессии есть взаимно простые натуральные числа, то она содержит бесконечное множество простых чисел.

Пусть

mn + l , n = 1,2, …,

прогрессия, удовлетворяющая условию теоремы.

Условие (m , l )=1, наложенные на числа m и e в формулировке теоремы, естественно, поскольку в случае, когда d =(m , l )1, все члены прогрессии делятся на d и поэтому не являются простыми числами.

Сформулированная теория была впервые высказана Л. Эйлером в 1783 г. В 1798 г. А. Лежандр опубликовал доказательство для четных m , использовавшее, как выяснилось позднее, одну ошибочную лемму.

Полностью доказал теорему в 1837–1839 гг. Петер Густав Лежен-Дирихле (1805–1859), немецкий математик, автор трудов по аналитической теории чисел, теории функций, математической физике.

В 1837 г. вышли две работы Дирихле, посвященные теореме о простых числах в арифметической прогрессии. Они содержали формулировку теоремы в общем виде, однако доказательство приводилось только для случая, когда разность прогрессии есть простое число. В конце второй работы содержится построение характеров для произвольного модуля и некоторые утверждения о том, как можно доказать утверждение L (1,)0 для неглавных характеров x в одном случае. В 1839 г. Дилихле опубликовал полное доказательство теоремы о простых числах в арифметической прогрессии. С тех пор она носит его имя.

1. Характеры

1.1 Определение характера. Основные свойства характеров

Характером (от греческого хараp-признак, особенность) конечной абелевой группы G называется не равная тождественно нулю комплекснозначная функция, определенная на этой группе и обладающая тем свойством, что если, АG и BG

(АВ)= (А) (В).

Обозначим через Е единичные элементы в группе G и через А^-1 обратный элемент для АG

Характеры группы G обладают следующими свойствами :

1 . Если Е-единица группы, то для каждого характера

(Е)=1 (1.1)

Доказательство . Пусть для каждого элемента АG справедливо неравенство

c₁ (А)=c(АЕ)= c(А) (Е)

Из этого равенства получим, что c (Е)0. Теперь из равенства

c (Е)= c (ЕЕ)= c (Е) c (Е)=1

следует равенство (1.1)

2 . c (А) 0 для каждого АG

Действительно, если бы (А) =0 для некоторого АG , то

c (А) (А^-1 )= c (АА^-1 )= (Е)=0,

а это противоречит свойству 1.

3 . Если группа G имеет порядок h, то А^h =Е для каждого элемента АG Следовательно,

1= (Е)= (А^h )= (А)^h ,

то есть (А) есть некоторый корень степени h из единицы.

Характер _1, обладающий свойством ₁ (А)=1 для каждого элемента АG, называется главным характером группы G . Остальные характеры называются неглавными.

Лемма 1. Пусть Н подгруппа конечной абелевой группы G , причем G / H – циклическая порядка n , тогда для каждого характера _H – подгруппы Н существует ровно n характеров.

Доказательство . Рассмотрим группу G = g^k H , причем gⁿ H=H, gⁿ H и gⁿ =h₁ =1.

Для каждого элемента XG существует и притом единственное к=к_х и h_х =h такое, что если 0 к_х n, то X= g^{k х} h_х =g^k h. Возьмем еще один элемент группы G , Y= g^m h_y , где 0mn. Перемножим эти два элемента

ХY= g^{к+ m} hh_y .

Определим характер (X).

(X)= (g^к h)= (g^к ) (n)= ^к (g) _H (h).

В данном выражении неизвестным является (g).

ⁿ (g)= (gⁿ )= (h₁ )= _H (h₁ ) – данное число.

( g )= – n корней из 1,

то есть _ј ⁿ =ⁿ (g)= _H (h₁ ), получаем x^k (g)= _ј ⁿ . Следовательно, x(g)= ₁ , …, _n

Из полученных равенств получаем:

(X)= ^k (g) _H (h_x )= _j ^kx _H (h_x )

(Y)= ^m (g) _H (h_y )= _j ^ky _H (h_y )

Определим умножение характеров

(X) (Y)= _j ^ky _H (h_y ) _j ^{k - x} _H (h_x )= _j ^{kx + ky} _H (h_x ) _H (h_y )= _j ^{k + m} _H (hh_y )

Для того чтобы определение выполнялось, необходимо рассмотреть степень g^{kx + kx} . Возможны два случая:

1) Если 0 к_х + k_y n, то

к_х + k_y = k_{xy ,} ; h_x h_y = h_{xy .}

В этом случае определение выполняется.

2) Если n к_х + k_y 2n-1, то получим

к_х + k_y = n + k_{xy .} .

Тогда

XY= g^{kx + ky} h_x h_y =g^h g^{kx + ky - n} h_x h_y =g^{kx + ky - n} h₁ h_x h_y

В свою очередь 0 к_х + k_y – nn-1 k_x +k_y – n=k_xy , h₁ h_x h_y = h_xy .

(XY) = _j ^{k х+ k у} _н (h_{x у)} = _j ^{k х + k у – n} _н (h₁ ) _н (h_x ) _н (h_y ) = _j ^кх _j ^ку _j ^{– n} _н (h₁ ) _н (h_x ) _н (h_y ) = _j ^кх _н (h_1х ) · _j ^ку _н (h_y ) = (X) (Y).

Лемма доказана.

5. Характеры конечной мультипликативной абелевой группы G образуют конечную мультипликативную абелевую группу .

Под произведением двух характеров и х группы G будем понимать характер х, определяемый следующим свойством:

(AB) = (A) (В)

Для любого элемента АG, имеем:

(АВ) = (АВ) (АВ) = (А) (В) · (А) (В) = (А) (В)

Таким образом, получаем действительно является характером.

Роль единичного элемента группы G играет главный характер ₁

Обратным элементом G является:

₂ (g₁ g₂ ) = == = ₂ (g₁ ) ₂ (g₁ )

1.2 Суммы характеров. Соотношение ортогональности

Пусть G – конечная мультипликативная абелева группа порядка h. Рассмотрим сумму:

S = ,

где А пробегает все элементы G, и сумму

Т =

где c пробегает все элементы группы характеров .

Рассмотрим чему равна каждая из сумм.

а) Если В-фиксированный элемент группы G и А пробегает все элементы G, то АВ также пробегает все элементы группы G. Следовательно,

S·c (В) = c (В) = = = S.

Получили Sc (В) = S, откуда следует, что (c (В) – 1)·S = 0. Следовательно, возможны два варианта:

1) S = 0, то c (В) – негативный характер

2) S0, то c (В) = 1 для каждого элемента В€Gи в этом случае c (В)= c₁ (В) есть главный характер и сумма S равна порядку h группы G. Таким образом,

S = = {(1.2)

б) Если мы умножим сумму Т на некоторый характер c’ группы , то аналогичным образом получим

c’ (А) Т = c’ (А) = = Т,

Следовательно,

1) или Т = 0, то А Е

2) или Т 0, то c’ (А) = 1 для каждого характера c’€ G. В этом случае согласно свойству 3§ 1, имеем А=Е. И тогда Т=h. Таким образом,

Т = = {

1.3 Характеры Дирихле

Пусть m – положительное целое число. Определим числовые характеры по модулю m. Мы знаем, что j(m) приведенных классов вычетов по модулю m образуют мультипликативную абелеву группу порядка h=j(m). Мы можем, следовательно, рассмотреть характер этой группы. Но определение характера для приведенных классов вычета по модулю mможно перенести на множество целых чисел следующим образом. Положим

c(а)= c(А), если аА,

где А – приведенный класс вычетов по модулю m. Тогда очевидно, c(а)= c(b) (modm), и c(ab)= c(а) c(b), если (а, m)=(b, m)=1. Поскольку c(А)0 для каждого приведенного класса вычетов А, то c(а)0, если (a, m)=1.

Это определение применимо только к целым числам а, которые взаимно просты с m.

Мы можем рассмотреть его на все целые числа, положив

c(а)=0, если (a, m)1.

Следовательно, характер по модулю m есть арифметическая функция c, обладающая следующими свойствами:

c(а)= c(b), если с=b (modm)

c(ab)= c(a) c(b) для всех целых a и b

c(а)=0, если (a, m)1

c(а)0, если (a, m)=1

Имеется точно j(m) – количество характеров по модулю m, где j(m) – количество положительных целых чисел, не превосходящих m и взаимно простых с m. Они образуют мультипликативную абелеву группу приведенных классов вычета по modm. Единичным элементом этой группы будет главный характер c_1, то есть такой характер, что c₁ (а)=1, если (а, m)=1. Далее имеем следующее соотношение ортогональности:

= {

= {

Пусть m – положительное целое число. Определим числовые характеры по модулю m. Комплекснозначная функция, определенная для всех целых чисел n, называется числовым характером или характером Дирихле по модулю m, она удовлетворяет следующим условиям:

а) c (n) = 0 тогда и только тогда, когда (n, m) 1

б) c (n) периодична с периодом m

в) для любых чисел а и b

c (аb) = c (а) c (b)

Функция

c₁ (n) = {

является числовым характером и называется главным характером . Остальные числовые характеры по модулю m называются неглавными.

Имеет место следующее утверждение о числовых характерах.

Теорема 1 Существует равно (m) числовых характеров по модулю m. Если c = c (n) – числовой характер по модулю m, то:

1) для n, взаимно простых с модулем m, значения c (n) есть корень из 1 степени (m).

2) для всех n выполняется неравенство /c (n)/ 1

3) Имеет место равенство

{

4) Для каждого целого числа n

= {

Доказательство. Пусть c (n) – некоторый числовой характер по модулю m. Из пункта б) определения следует, что c (n) задает некоторую функцию c’() = c (n) на мультипликативной группе классов вычетов по модулю m, взаимно простых с m, а именно

c’() = c (n)

Здесь обозначает класс вычетов по модулю m, содержащий n. Так как c(1) 0, то c’() не равняется тождественно нулю, а из пункта в) определения числового характера следует, что c’() = c’() = c’ (ab ) = c (a ) c (b ) = c’()c’().

Таким образом, c’() есть характер модультипликативной группы G_{m .}

Обратно, по каждому характеру c’() группы G_m можно построить числовой характер c (n) по модулю m, положив

{

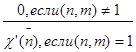
Установленное соответствие является взаимнооднозначным. И все утверждения теоремы 1 следуют из доказанного выше для групповых характеров применительно к группе G_m , если учесть, что порядок группы G_m равен (m), где (m) – функция Эйлера.

В дальнейшем требуется еще одно утверждение с числовых характерах. Обозначим для каждого c, c 1

Где суммирование ведется по всем натуральным числам n, не превосходящим c.

Лемма 2. Пусть c (n) – неглавный характер. Тогда для каждого c, c 1 справедливо неравенство

/S(x)/m

Доказательство. Функция c (n) периодична с периодом m и по теореме з

0, так как c c₁

Поэтому, представив [c] – целую часть числа c – в виде [c]=m1+z, 0zm, будет иметь

S(c) =S([c])=q

В виду равенства /c(n)/1 отсюда получили S(c)zm

2. L-функция Дирихле

Пусть х(п) – произвольный характер по модулю m. Рассмотрим ряд

, (2.1)

члены которого являются функциями комплексного переменного S. В области сходимости он определяет функцию, которая называется L-функцией Дирихле, соответствующей характеру c(n), и обозначается L (s, c).

Лемма 3

1. Если cc₁ , то ряд (1) сходится в области ReS 0 и определяемая им функция L (s, c) является аналитической в этой области.

2. Ряд, определяющий L (S, c₁ ), сходится в области ReS 1. Функция L(S, c₁ ) является аналитической в области ReS 1.

Доказательство.

Пусть c(n) – произвольный характер по модулю m, а б – некоторое положительное число. Так как /c(n)/ 1, то в области ReS 1 + б справедливо неравенство

Следовательно, ряд (1) равномерно сходится в области ReS 1 + б. Определяемая им функция L (S, c) по теореме Вейерштрасса о сумме равномерно сходящегося ряда аналитических функций является аналитической в этой области. Ввиду произвольности 6 это доказывает второе утверждение Леммы.

Для неглавных характеров c(n) потребуется более сложное исследование ряда (1).

Лемма 4 (преобразование Абеля).

Пусть a_n , n=1,2,…, – последовательность комплексных чисел, c1,

А(c)=

а q(t) – комплекснозначная функция, непрерывно дифференцируемая на множестве 1t

Тогда

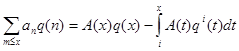(2.2)

Если же

то

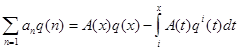(2.3)

при условии, что ряд в левой части равенства сходится.

Доказательство. Положим А(0)=0 и В(х) равным левой части равенства (2.2). Тогда при любом натуральном N

так как А(0)=0. Далее

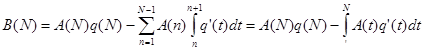
поскольку функция А(х) постоянна на каждом полуинтервале ntn+1. Следовательно, равенство (2.2) доказано при целых значениях х.

пусть х1 – произвольное число. Положим N=[x]; значит, NxN+1. Тогда А(х)=А(N), B(x)=B(N), а

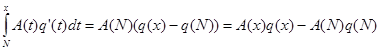
Следовательно,

Тем самым доказано, что равенство (2.2) верно и для нецелых чисел значений х.

Равенство (2.3) получаем из равенства (2.2) переходом к пределу при х®. Лемма доказана.

Воспользовавшись леммой 4, получим следующее равенство

(2.4)

где

функция, введенная Лемме 4.

Для s = p+it из области ReS = s, где s – некоторое положительное число, пользуясь леммой 4, находим

Поэтому интеграл

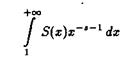
сходится в области ReS s. Поскольку в этой области выполняется неравенство

то из равенства (2) следует, что ряд (1), определяющий функцию L (S, x), сходится в области ReS s. Эти рассуждения справедливы для любого положительного числа s. Значит, ряд (1) сходится в полуплоскости ReS 0.

Из равенства (2) следует, что в этой полуплоскости для L-функции, соответствующей неглавному характеру c(n), справедливо представление

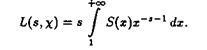
(2.5)

так как

Интеграл, стоящий в правой части равенства (2.5), можно также представить в виде

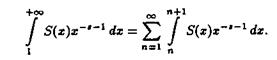(2.6)

Члены ряда (2.6) являются аналитическими функциями в области ReS s, что следует из равенств

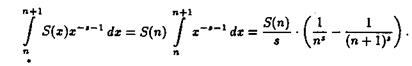
При этом использовано, что на полуинтервале nх n+1 функция S(х) принимает значение S(n). Поскольку

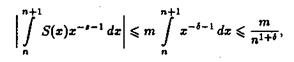
то ряд (2.6) равномерно сходится в области ReS s. Отсюда, как и выше, получаем, что сумма его, т.е.

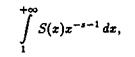
является аналитической функцией (по теореме Вейерштраса) в области ReS s.

Из представления (2.5) следует теперь, что L (S, x) есть аналитическая функция в полуплоскости ReS s, а ввиду произвольности S – s и b полуплоскости ReS 0.

Следствие. Пусть c (n) – произвольный характер. Тогда в области ReS 1 справедливо равенство

(2.7)

Это следует из того, что ряд (2.1) по доказанному равномерию сходится в области ReS1+s, где s0. Следовательно, по теореме Вейштрасса о равномерно сходящихся рядах аналитических функций в этой области ряд (2.1) можно почленно дифференцировать

Поэтому в полуплоскости ReS1+s выполняется равенство (2.7). Так как в этом рассуждении s-любое положительное число, то равенство (2.7) будет справедливо в полуплоскости ReS1.

Для L-функций имеет место представление в виде бесконечного произведения по простым числам, аналогичное тождеству Эйлера. Рассмотрим вспомогательную Лемму.

Лемма 5. Пусть функция f(n) вполне мультипликативна и ряд

(2.8)

абсолютно сходится. Тогда выполняется равенство

(2.9)

Доказательство. Отметим прежде всего, что /f(n)/1 при любом натуральном n1. В противном случае при каждом mN

/f(n)^m /=/f(n)/^m 1,

что противоречит сходимости ряда (2.6). Поэтому при каждом простом р ряд

абсолютно сходится, и его сумма как сумма бесконечно убивающей геометрической прогрессии равна (1-f(р))^-1. Кроме этого, в силу абсолютной сходимости, ряды можно перемножить. Перемножая конечное число таких рядов и используя то, что f(n) есть вполне мультипликативная функция, получим

где n_e = p^a … p^a s и в сумме в правой части равенства содержатся такие и только такие слагаемые f(n_e ), что все просты делители n_e не превосходят х. Следовательно, в разности

остаются те и только те слагаемые f(m_e ), для которых у числа m_e имеется хотя бы один простой делитель рx. Тогда оценим разность

/S-S(x)/

и из абсолютной сходимости ряда (2.8) следует, что

Это доказывает, что бесконечное произведение (2.7) сходится и выполняется утверждение Леммы.

Лемма 6. Для каждого характера c(n) в области ReS 1 справедливо представление

Доказательство. Эта лемма является следствием Леммы 5, поскольку функция c(n) вполне мультипликативна, то есть c(АВ)= c(А) c(В), и выполняется неравенство /c(n)/ 1 по теореме 1.

Следствие 1. В области ReS 1 для главного характера c₁ (n) по модулю m справедливо равенство

(2.10)

и поэтому функция L (S, c₁ ) может быть аналитически продолжена в область ReS 0, где она имеет единственный полюс (первого порядка) в точке S=1.

Действительно, по определению главного характера c₁ (n) имеет место равенство

Поэтому

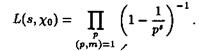
Пользуясь теперь тождеством Эйлера для дзета-функции Римана получаем равенство (2.10). Остальные утверждения легко следуют из этого равенства, поскольку дзета-функция является аналитической в области ReS 0 с единственным полюсом первого порядка в точке S = 1.

Следствие 2. Для каждого характера c функция L (S, x) не обращается в нуль в области ReS 1.

Доказательство.

Если s = ReS 1. то

Пользуясь неравенством для дзета-функции Римана, находим

Получаем:

L(S,c) 0

Теперь докажем утверждения, что L – функция, соответствующая неглавному характеру c, точке S =1 отлична от нуля.

Теорема 2. Если c – неглавный характер, то L(1, c)0

Для доказательства рассмотрим 2 случая

1. Пусть характер c – комплексное число, не является действительным. Тогда характер c² (n) не является главным. В этом случае доказательство теоремы будет основываться на тех же идеях, что и доказательство отсутствия нулей дзета – функции на прямой ReS=1.

Лемма7. Пусть 0ч 1, а х – действительное число, тогда выполняется неравенство /(1 – ч )³ (1 – че ^ix )⁴ (1 – че^{2 ix} )/^-1 1

Доказательство.

Для всех z из круга /z/1 имеет место расположение

– ln (1 – z) =(2.11)

Так как ln(t) = Relnt, то обозначая М (ч ), левую часть неравенства (2.11), получим

lnM(ч ) = 3ln(1 – ч ) – 4 ln (1 – че ^{i 4} ) – ln (1 – че^{2 i 4} ) = – 3ln(1-ч ) – 4Reln/1 – че ^{i 4} / – Reln/1 – че^{2 i 4} /=rc(3+4e)^inl /1-re^{i 4} /= (3+4cosnl+2cos2nl)= (2+4cosa+1+cos2a)=1 (1+cosa)² 0

ln=M(r, l)=0

Следовательно, M(r, l)=1 доказана.

Из леммы 7 следует, сто при любом действительном S1 выполняется равенство:

| L ³ (8, c₁ ) L ⁴ ( S , c) 4 ( S , c⁴ ) 1 = П (1- )³ (1- )⁴ (1- )|^-1 (2.12)

Получая в лемме ч = р ^{- s} , т.е.

0 ч = c₁ (р) 1

0 р ^{- s} 1

c (р) р^{- s} = че ^{i 4} , в силу того что c (р) – комплексное

c (р) р^{- s} = че^{2 i 4}

Получаем, что каждый сомножитель в правой части равенства (f) не меньше 1 и, следовательно, при любом S1 выполняется равенство:

|L³ (Sc₁ ) · L⁴ (Sc) L(Sc² )| 1 (2.13)

Допустим, что для некоторого характера c (c² c₁ ) выполняется равенство

L (1, c) = 0 (2.14)

Оценим сверху левую часть неравенства. Из оценки дзета-функции Римана

(S) , следует, что при S € R, S1 выполняется неравенство

а) 0 4 (S, c₁ ) =

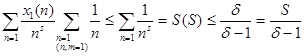
получили 0L(S, c₁ )

б) Функция L(S, c) разложим в ряд Тейлора

L (S, c) = C_p + C₁ (S – 1) + C₂ (S – 1)² +… + C_n (S – 1)ⁿ +…

Предположим, что у нее есть нуль L(1, c) = 1; тогда С₀ = 0

Перепишем разложение L – функции в ряд

L(S^c ) = C_к (S – 1)^к + С_{к +1} (S – 1)^{к +1} = (S – 1)¹ (C_к + С_{к +1} (S -1)+….), гдек1, С_к 0, т. к. S1

| L (S, c)| = |S – 1|^k | C_k + C_k+1 (S – 1) +….| 2 C_k |S – 1)^k , при |S – | r

Функция L (S, c² ) в точке S = 1 не имеет полюса, следовательно не имеет особенности. Это в силу того, что c комплексное и c² c₁

Получаем неравенство:

L(S, c² ) C,

При условии | S – 1|

Учитывая все неравенства и оценки

| L³ (S, c) L⁴ (S, c) L (S, c² )| = ()³ · 2⁴ |C_k |⁴ (S – 1)^4k · C1

Следовательно, это неравенство становится противоречивым, если перейти к пределу при S1+0. Полученное противоречие показывает, что равенство (2.14) не выполняется.

2. Рассмотрим c – вещественный характер, т.е. принимающий только вещественные значения, несовпадающий с главным характером

Лемма 8. Пусть c – вещественный характер.

Рассмотрим функцию

F(S) = (S) L(S, x) (2.15)

Докажем, что если ReS1, то

(2.16)

представляется рядом Дирихле, которого справедливы следующие утверждения:

1) Все коэффициенты а _n 0

2) при n=k² , k € / N(N)/ а _n 1

3) В области ReS1 можно почленно дифференцировать, то есть

F^{( k )} (S)= (-1)^k (lnn)^k k=1,2…; (2.17)

4) Ряд (1) в точке S=1/2 расходится.

Доказательство. В области ReS 1 ряды, определяющие функции S(S) и L(S,c), абсолютно сходятся, поэтому их можно перемножить:

где

(2.19)

Пусть - расположение числа n в произведение простых сомножителей. Тогда все натуральные делители l числа n имеют вид

поэтому из равенства (14) находим, что

гдеa_{ni =} 1+ c (p_i )+ … +c^Li (p_i ), i=1,…, m (2.21)

так как c – вещественный характер, то он может принимать только три значения: 0, 1, -1. Из равенства (2.21) следует, что

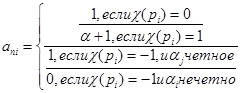(2.22)

Во всех случаях числа a_ni 0, а значит, и a_n =a_n 1 … a_nm 0

Если же число п является полным квадратом, то

N=k² =p_/ ^{2 g} … p_m ^{2 g ,}

и из равенств (2.20) и (2.22) следует, что а_n 1

При любом s 0 в области ReS 1 +s выполняется неравенство

Ряд (2.18) сходится в области ReS 1. Поэтому по признаку Вейерштрасса ряд (2.16) сходится равномерно в области ReS 1 + s, а по теореме Вейерштрасса его можно в этой области почленно дифференцировать любое число раз. Следовательно, в области ReS 1 +s выполняется равенство (2. 17), а в силу произвольности s оно выполняется и в области ReS 1.

Однако ряд (39) расходится, так как по второму утверждению леммы

Ряд (2.16) при S = имеет неотрицательные члены. Поэтому, если бы он сходился, то также сходился бы ряд

(2.23)

Следовательно, ряд (2.23) расходится. Лемма доказана.

Переходим непоредственно к доказательству второго случая теоремы. Допустим, что L (1,c) = 0. Тогда полюс дзета-функции будет компенсироваться в произведении S(S) L (S, c) нулем функции L (S, c).

Поэтому функция (2.15) F(S) будет аналитической в области ReS 0 так как в точке S=1 у F(z) – устраненная особая точка. Следовательно, ее можно разложить в ряд Тейлора в точке S = 2:

(2. 24)

радиус сходимости которого не меньше 2 R2/

Из равенств (2.17), в частности S=2, находим

(2.25)

В радиусе сходимости будет брать не все S, а только вещественные ReS=sS=s(0,2). Пользуясь разложениями (18) и (19), находим

Члены двойного ряда неотрицательны, поэтому он сходится абсолютно, и в нем можно поменять порядок суммирования. Тогда

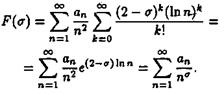
Следовательно, ряд (2.16) сходится во всех точках, s (, 0, 2), и в точке , а это противоречит четвертому утверждению леммы. Поэтому L(S,c)0/

Этим завершается доказательство теоремы

По следствию 2 леммы 2 функция является аналитической в области ReS 1. Для дальнейшего доказательства теоремы Дирихле нам будет необходимо представление этой функции в виде ряда, аналогичного ряда (2.16).

Лемма. Для каждого характера c(n) в области ReS 1 справедливо равенство

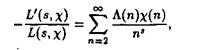(2.26)

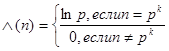
Доказательство.

Так как S=s+it имеет место неравенство

получаем, что ряд стоящий в правой части равенства (2.26), абсолютно сходится в области s1. Умножим этот ряд на ряд определяющий L (S, c). Получили

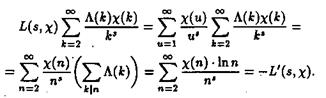
Предпоследнее равенство имеет место ввиду равенства ), а последнее – по следствию из леммы 3, равенство 2.7.

3. Доказательство теоремы Дирихле

Теорема. Если разность и первый член арифметической прогрессии есть взаимно простые натуральные числа, то она содержит бесконечное множество простых чисел.

Доказательство.

Рассмотрим равенство (2.26), которое справедливое по Лемме в области ReS 1. Поскольку (n) = 0 для всех n, не являющихся степенями простых чисел, то все отличные от нуля члены ряда в правой части (2.26) имеют вид

где р – простое и k– натуральное числа. Ряд (2.26) абсолютно сходится, следовательно, его можно представить в виде двойного ряда) и, значит, в области ReS 1

(3.1)

Второе слагаемое в правой части этого равенства равномерно ограничено по s в области ReS3/4. Действительно, если S=p+it, p3/4, то

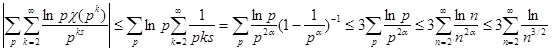
Следовательно, при S®1+0 для каждого характера c имеет место равенство

(3.2)

Здесь и в дальнейшем s ® 1 + o обозначает, что S стремится к 1 по действительной оси справа.

Пусть u – некоторое натуральное число, удовлетворяющее сравнению

(3.3)

Умножим обе части равенства (3.2) на c(u) и просуммируем получившиеся равенства по всем числовым характерам c. Тогда получим

(3.3)

Если простое число р удовлетворяет сравнению р l (mod m), то pu 1 (mod m), и по теореме 1

Если же pl (modm), то pu 1 и по той же теореме

Таким образом, равенство (3.3) можно переписать в виде

(3.4)

По лемме 3 и теореме 2 для неглавного характера c функция является аналитической в точке S = 1. Поэтому для таких характеров при S®1 + 0 имеем

(3.5)

По следствию 1 леммы 4 функция L(S, c₁ ) имеет в точке S=1 полюс первого порядка. Значит, при S®1+0

(3/6)

Учитывая равенства (3.5) и (3.6.) из равенства (26) получаем, что

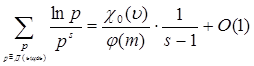
Так как число u удовлетворяет сравнению (3.3), то (u, m) = 1 и c₀ (u)=1. Итак, при S®1+0

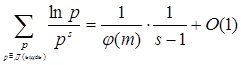(3.7)

Правая часть равенства а (3.7) при S®1+0 имеет бесконечный предел. Значит, сумма, стоящая в левой части этого равенства, имеет бесконечное множество слагаемых. Поэтому существует бесконечное множество простых чисел, удовлетворяющих сравнению

pe (modm)

Теорема Дирихле доказана.

Скачать архив с текстом документа