Физика движения тела
СОДЕРЖАНИЕ: КОНТРОЛЬНАЯ РАБОТА ПО ФИЗИКЕ Задача 1. Точка движется прямолинейно на плоскости по закону Каковы начальная скорость и ускорение точки? Найти мгновенную скоростьКОНТРОЛЬНАЯ РАБОТА ПО ФИЗИКЕ
Задача 1.
Точка движется прямолинейно на плоскости по закону ![]()
Каковы начальная скорость и ускорение точки? Найти мгновенную скорость
точки в начале пятой секунды движения.
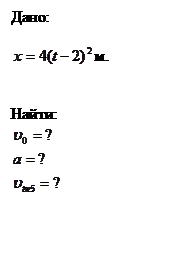
![]()
Решение:
1) Т.к. ![]() ,то
,то
![]()
![]() при
при ![]()
![]() м/с.
м/с.
2) Т.к. ![]() , то
, то
![]() м/с.
м/с.
3) При ![]() , т.к. до начала 5 с прошло 4 с.
, т.к. до начала 5 с прошло 4 с.
![]() м/с.
м/с.
Ответ:
Начальная скорость точки ![]() м/с, ускорение
м/с, ускорение ![]() м/с, скорость точки в начале
м/с, скорость точки в начале
пятой секунды движения ![]() м/с.
м/с.
Задача 2.
Найти радиус R вращающегося колеса, если известно, что линейная скорость v1 точки,
лежащей на ободе, в 2,5 раза больше линейной скорости v2 , точки, лежащей на расстоянии
r =5 cм. ближе к оси колеса.

Решение:
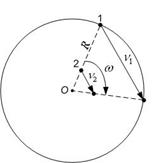 1) У точек находящихся на
1) У точек находящихся на
колесе и лежащих на радиусе,
будут одинаковы угловые ско-
рости. Используем связь угловой
и линейной скоростей:
![]() и
и ![]()
т.к. ![]() , приравниваем правые
, приравниваем правые
части уравнений:
![]()
Решим уравнение относительно ![]() :
:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]()
Ответ: Радиус вращающегося колеса равен 8,33 см.
Задача 3.
Под действием силы F
= 10 Н тело движется прямолинейно так, что зависимость пройденного телом пути S
от времени t
дается уравнением ![]() , где С
= 1 м/с2
.
, где С
= 1 м/с2
.
Найти массу m тела.
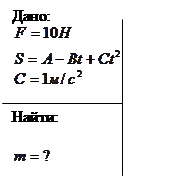
Решение:
1) Известно, что зависимость пути от времени выражается
формулой:
![]() отсюда имеем:
отсюда имеем:
![]() ,
, ![]() ,
, ![]() .
.
2) По условию:
![]() следовательно:
следовательно:
![]()
3) Из второго закона Ньютона: ![]() отсюда:
отсюда:
![]() кг.
кг.
Ответ: Масса тела равна 5кг.
Задача 4.
Из ружья массой m1 = 5 кг вылетает пуля массой m2 = 5 г со скоростью v2 = 600 м/с.
Найти скорость v2 отдачи ружья.
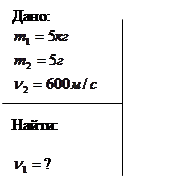 Решение:
Решение:
1) По закону сохранения импульса:
![]()
![]() при этом
при этом ![]() то:
то:
![]() ;
;
![]() ;
;
![]() отсюда:
отсюда:
![]()
Ответ:
Скорость отдачи ружья составляет ![]()
Задача 5.
Вагон массой m = 20 т, двигаясь равнозамедленно с начальной скоростью v0 = 54 км/ч,
под действием силы тренияFmp = 6кН через некоторое время останавливается. Найти работу A
сил трения и расстояние S , которое вагон пройдет до остановки.

Решение:
1) Работа А, совершаемая результирующей силой, может быть определена как мера изменения кинетической энергии материальной точки:
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
![]() ;
;
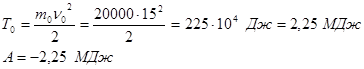
2) ![]() ; выполним проверку размерности:
; выполним проверку размерности: 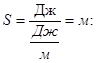
![]()
Ответ:
Работа сил трения равна ![]() , расстояние которое вагон пройдет до
, расстояние которое вагон пройдет до
остановки ![]() .
.
Задача 6.
Тело массой m1 = 5 кг ударяется о неподвижное тело массой m2 = 2,5 кг. Кинетическая
энергия системы двух тел непосредственно после удара стала wк = 5 Дж. Считая удар центральным и неупругим, найти кинетическую энергию wк1 первого тела до удара.

Решение:
1) Используем закон сохранения импульса:
![]()
Где ![]() - скорость первого тела до удара;
- скорость первого тела до удара;
![]() - скорость второго тела до удара;
- скорость второго тела до удара;
![]() - скорость движения тел после удара.
- скорость движения тел после удара.
![]() т.к. по условию второе тело до удара неподвижно
т.к. по условию второе тело до удара неподвижно
2) ![]() ;
;
Т.к. удар неупругий, то скорости двух тел после удара равны, т.о. выразив ![]() через
через ![]() , получим:
, получим:
![]() ;
; ![]() ;
; 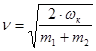 .
.
3) Отсюда имеем:
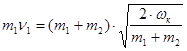 ;
;
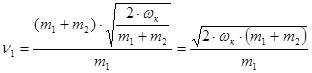 - скорость первого тела до удара.
- скорость первого тела до удара.
4) Подставив данное значение, найдем кинетическую энергию первого тела до удара:
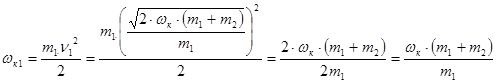
5) Выполним проверку размерности:
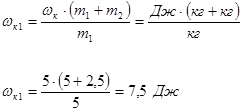
Ответ:
Кинетическая энергия первого тела до удара ![]()
Задача 7.
К ободу диска массой m = 5 кг приложена касательная сила F = 19,6 Н. Какую кинетическую энергию wк будет иметь диск через время t = 5 c после начала действия силы?
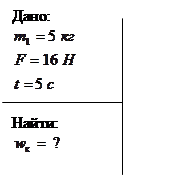
Решение:
1) 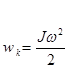 - кинетическая энергия диска;
- кинетическая энергия диска;
2) ![]() - угловая скорость;
- угловая скорость;
3) 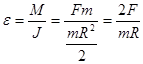 - угловое ускорение;
- угловое ускорение;
4) Момент инерции для диска ![]() ;
;
5) 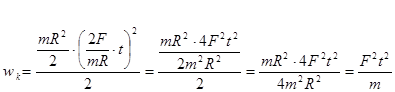
6) Выполним проверку размерности:
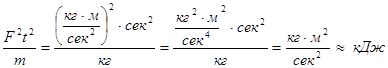
7) Подставив данные, получим :
![]()
Ответ:
Кинетическая энергия, через 5 с. после начала действия силы будет равна ![]() .
.
Задача 8.
Сколько полных колебаний должен совершить маятник, логарифмический декремент затухания которого 0,54, для того, чтобы амплитуда его колебаний уменьшилась в три раза?
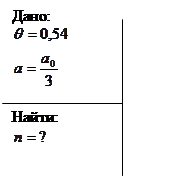
Решение:
1) ![]()
![]() -число колебаний с амплитудой
-число колебаний с амплитудой ![]() , где
, где ![]() -
-
основание натурального логарифма ![]()
2) ![]() - число колебаний
- число колебаний
Ответ: маятник должен совершить три полных колебания.
Задача 9.
Вода при температуре t = 4 0 C занимает объём V = 1 см3 . Определить количество вещества v и число N молекул воды.
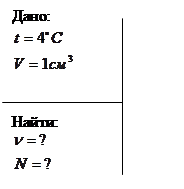 Решение:
Решение:
1) ![]()
Молярная масса воды ![]()
Плотность воды при ![]() равна
равна ![]()
![]()
![]() - количество вещества
- количество вещества
2) ![]() -число молекул.
-число молекул.
Ответ:
при ![]() в объеме воды
в объеме воды![]() количество вещества
количество вещества![]() ,
,
а число молекул ![]()
Задача 10.
Найти внутреннюю энергию w массы m = 20 г кислорода при температуре t = 20 0 C
Какая часть этой энергии приходится на долю поступательного движения молекул, и какая на
долю вращательного движения?
 Решение:
Решение:
 1)
1) ![]() где
где ![]() - число степеней
- число степеней
свободы ![]() т.к. кислород является
т.к. кислород является
двухатомным газом.
2) ![]()
3) ![]()
4) выполним проверку размерности:
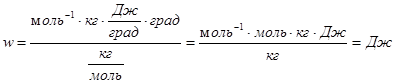
5) ![]()
6) Поскольку кислород является двухатомным, он имеет пять степеней свободы,
из них три приходится на поступательное и две на вращательное движение, отсюда:
![]()
![]()
Ответ:
внутренняя энергия кислорода массой 20 гр. при t=10![]() равна 9,9 кДж, при этом на
равна 9,9 кДж, при этом на
долю поступательного движения приходится ![]() всей энергии, т.е. 5,94 кДж, а на долю
всей энергии, т.е. 5,94 кДж, а на долю
вращательного движения, соответственно, приходится ![]() всей энергии т.е. 3,96 кДж.
всей энергии т.е. 3,96 кДж.
Задача 11.
При некоторых условиях средняя длина свободного пробега молекул газа ![]()
средняя арифметическая скорость его молекул ![]()
Найти среднее число столкновений Z в единицу времени молекул этого газа, если при той же
температуре давление газа уменьшить в 1.27 раза.
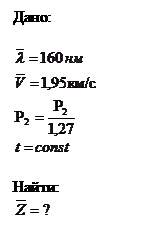
![]() Решение:
Решение:
1) 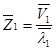 ;
; 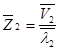 ;
; ![]() т.к. скорость – производная от
т.к. скорость – производная от
температуры, а ![]() по условию.
по условию.
2) Составим пропорцию:
![]()
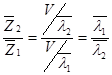 т.к.
т.к. 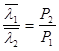 , то
, то ![]()
3) Решим полученное равенство относительно ![]() :
:
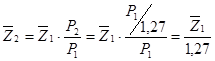 ;
; 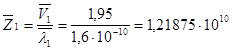
![]()
4) Выполним проверку размерности:
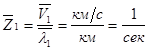
Ответ:
если при ![]() давление газа уменьшить в 1,27 раза то среднее число
давление газа уменьшить в 1,27 раза то среднее число
столкновений будет равно ![]() раз в секунду.
раз в секунду.
Задача 12.
Идеальная холодильная машина, работающая по обратному циклу Карно, совершает за один цикл работу А = 37 кДж. При этом она берет тепло от тела с температурой t2 = - 10 0 C
и передаёт тепло телу с t1 = 17 0 C. Найти к.п.д. цикла, количество теплоты Q2 , отнятое у холодного тела за один цикл и количество теплоты Q1 переданное более горячему телу за один цикл.
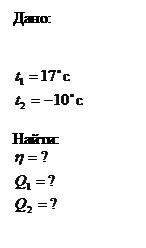 Решение:
Решение:

1) Найдем к.п.д. холодильной машины:
![]() где
где ![]()
![]() отсюда к.п.д. холодильной
отсюда к.п.д. холодильной
машины:
![]() ;
;
2) Известно, что к.п.д. это отношение произведенной работы к отданному теплу,
![]() отсюда
отсюда ![]() таким образом находим
таким образом находим ![]()
![]() - количество тепла переданного более горячему телу.
- количество тепла переданного более горячему телу.
3) Количество тепла отнятого у более холодного тела, определим через пропорцию:
![]() ;
; ![]() ;
;
![]() - количество тепла отнятого у более холодного тела.
- количество тепла отнятого у более холодного тела.
![]() Ответ: - к.п.д. холодильной машины
Ответ: - к.п.д. холодильной машины ![]()
- количество тепла переданного более горячему телу
![]()
- количество тепла отнятого у более холодного тела