Гідравлічні трубопроводи

СОДЕРЖАНИЕ: Основні формули для гідравлічного розрахунку напірних трубопроводів при турбулентному режимі руху. Методика та головні етапи проведення даного розрахунку, аналіз результатів. Порядок і відмінності гідравлічного розрахунку коротких трубопроводів.

Курсова робота

Гідравлічні трубопроводи

Вступ

Гідравліка – це технічна (прикладна) наука, що вивчає закони рівноваги і руху рідини та розробляє способи застосування цих законів для розв’язування цих задач.

Втрати напору в трубопроводах складаються з втрат по довжині і місцевих втрат. Залежно від впливу цих втрат трубопроводи поділяють на короткі і довгі.

До довгих належать трубопроводи, в яких визначальними є втрати по довжині, а місцеві втрати не перевищують 10–15% загальних втрат, а до коротких – трубопроводи з великою кількістю місцевих опорів, у яких визначальними є місцеві втрати, а втрати по довжині не перевищують 10–15% загальних втрат.

Довгі трубопроводи поділяють на прості і складні,

Прості трубопроводи – це трубопроводи сталого діаметра, що не мають відгалужень.

Складний трубопровід – це такий, що складається з окремих елементів: простих коротких або довгих трубопроводів. Прийнята класифікація трубопроводів дає змогу значною мірою спростити розрахунок їх.

Гідравлічний розрахунок трубопроводів полягає у визначенні витрати рідини, напору, діаметра труб при заданих інших величинах. Іноді за заданими витратою Q, діаметром і довжиною трубопроводу визначають напір Н або за тих же умов визначають витрату Q якщо задано напір Н. Діаметр трубопроводу d визначають, коли всі інші параметри відомі.

1. Основні формули для гідравлічного розрахунку напірних трубопроводів при турбулентному режимі руху

Гладкі труби

Коефіцієнт гідравлічного тертя l, що входить в розрахункову формулу для визначення втрат натиску по довжині

,

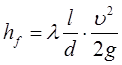для гладких труб знаходиться по емпіричних залежностях виглядуl=l (Re).

Для потоків, що характеризуються числами Re від 2300 до 100000, застосовується така залежність:

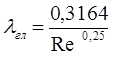. (1)

П.Н. Конаковим запропонована більш загальна формула, область вживання якої не обмежується величиною числа Re:

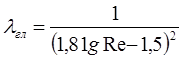(2)

Може бути використана формула Р.К. Филоненко

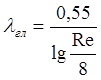
, (3)

яка дає практично однакові результати з формулою П.Н. Конакова.

Шорсткі труби

Для визначення втрат натиску в круглих шорстких трубах у разі квадратичної області опорів звичайно використовуються так звані водопровідні формули, одержувані ззалежності Шезі. Позначивши через l довжину труби, представимо формулу Шезі таким чином:

.

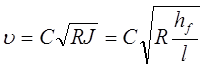Отже,

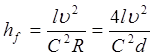. (4)

Помноживши у формулі (4) чисельник і знаменник на 2g одержимо остаточну формулу, яка може бути названа першою водопровідною формулою (формула Вейсбаха – Дарсі):

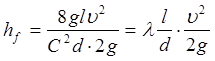, (5)

де коефіцієнт гідравлічного тертя.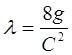

Визначаючи С по формулі Н.Н. Павлівського, одержимо.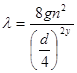

Замінимо в залежності (4) швидкість через

,

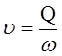де Q – витрата рідини, що проходить через трубу;

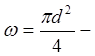площа живого перетину труби.

Одержимо формулу, яка може бути названа другою водопровідною формулою:

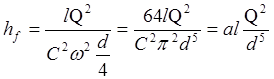; (6)

тут

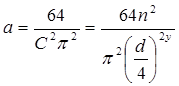. (7)

Для розрахунку труб рекомендується вживання коефіцієнтів шорсткості п , приведених в табл. 1.

Таблиця значень коефіцієнта шорсткості п для труб

Стан стінок труб і характерні умови експлуатації	п
Нові чавунні, металеві і гончарні труби при добрій укладці і з’єднанні	0,0110	90,9
Водопровідні труби в нормальних умовах експлуатації, бетонні труби в дуже гарному стані	0,0120	83,3
Трохи забруднені водопровідні труби, клепані стальні спіральні труби в дуже гарному стані, бетонні труби в гарному стані	0,0130	76,9
Забруднені водопровідні труби	0,0140	71,4
Клепані стальні спіральні труби в середніх умовах експлуатації	0,0150	66,7
Бетонні труби в поганому стані	0,0160	62,5
Азбестоцементні труби	0,0092	108,7
Поліетиленові труби	0,0086	116,4

Останнім часом рядом авторів складені таблиці значень коефіцієнта С, підрахованих по формулі Н.Н. Павловского для різних коефіцієнтів шорсткості і гідравлічних радіусів R.*

Для спрощення обчислень по формулах (5) і (6) для стандартних діаметрів труб приводяться таблиці значень коефіцієнтів ₁ = f ₁ (d) і а = f ₂ (d), обчислених при різних п із застосуванням формули Н.Н. Павлівського.

Формули (5) і (6) для розрахунків шорстких труб справедливі тільки для квадратичної області опорів. Відповідними дослідженнями встановлено, що труби великих діаметрів працюють переважно в доквадратичній області через малу їх відносну шорсткість. Квадратичний закон опору для труб великого діаметру буде справедливий тільки у випадку, якщо виступи шорсткості мають значну висоту.

У результаті обробки експериментального матеріалу для доквадратичної області Ф.А. Шевелев рекомендує для визначення гідравлічного ухилу користуватися формулою

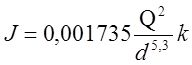, (8)

де k – поправочний коефіцієнт, залежний від середньої швидкості , причому Q виражається в м³ /с , а d в м .

Значення поправочного коефіцієнта k для сталевих і чавунних труб дані в табл. 2.

Таблиця 2. Значення поправочного коефіцієнта для сталевих і чавунних труб

, м/с	k	, м/с	k	, м/с	k
0,20	1,410	0,50	1,150	0,80	1,060
0,25	330	0,55	1,130	0,85	1,050
0,30	280	0,60	1,115	0,90	1,040
0,35	240	0,65	1,100	1,00	1,030
0,40	200	0,70	1,085	1,10	1,015
0,45	175	0,75	1,070	1,20	1,000

Приводимо експериментальні формули, що застосовуються для розрахунку:

азбоцементних труб (формула Ф.А. Шевелева):

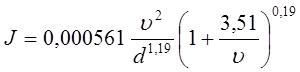; (9)

деревяних труб (формула Скобея):

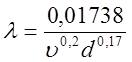, (10)

де виражається в м/с , а d в м .

2. Класифікація трубопроводів і основні задачі по їх гідравлічному розрахунку

Розглядатимемо турбулентний рух будь-якої рідини, що відповідає квадратичній області опору, маючи у вигляді при цьому тільки круглоциліндричні труби.

Гідравлічний розрахунок трубопроводів проводиться або з метою визначення діаметру трубопроводу, призначеного для пропуску певної витрати рідини, або з метою встановлення гідравлічних характеристик трубопроводу: втрат натиску і витрати рідини, що пропускається (при відомих діаметрі і довжині труби).

При гідравлічному розрахунку трубопроводів залежно від їх довжини і гідравлічних умов розрахунку розрізняють два типи трубопроводів: короткі і довгі.

Короткими трубопроводами називаються трубопроводи порівняно невеликої довжини, в яких місцеві втратиопору є достатньо істотними, складаючи не менше 5–10% від втрат опору по довжині. Прикладами коротких трубопроводів можуть служити всмоктуюча лінія відцентрового насоса, напірна водопропускна труба під залізничним насипом і т.п.

Довгими трубопроводами називають трубопроводи, що мають значну протяжність, в яких втрати опору по довжині є основними. У випадку довгих трубопроводів місцевими втратами звичайно нехтують, іноді ж їх приймають рівними 5–10% від втрат опору по довжині. Прикладами довгих трубопроводів можуть служити трубопроводи водопровідних мереж, а також трубопроводи, що використовуються при гідромеханізації і т.д.

Залежно від гідравлічної схеми роботи трубопроводи розділяються на прості , не мають відгалужень, складні – з відгалуженнями. Розрізняють також тупикові трубопроводи і замкнуті, або кільцеві. Замкнуті трубопроводи більш надійні в роботі, зокрема забезпечують безперебійне водопостачання при пошкодженні окремих ліній або виробництві ремонтних робіт.

При гідравлічному розрахунку трубопроводів звичайно зустрічаються наступні три основні задачі:

1) визначення витрати трубопроводу Q при заданих l , d, h_f ;

2) визначення втрати опору h_f при заданих l , d, Q;

3) визначення потрібного діаметру трубопроводу при заданних l , Q, h_f .

При рішенні цих і інших задач, повязаних з гідравлічним розрахунком трубопроводів, широко використовується поняття про витратну характеристику (про модуль витрати) труб. Витрата рідини при рівномірному русі визначається, по формулі.

або

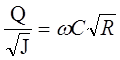
Для труби постійного перерізу , С, R – величини постійні. Тоді величина

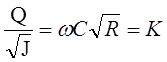
також постійна. Вона називається витратною характеристикою, або модулем витрати:

або (11)

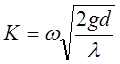
Витрата рідини

(12)

Оскільки ухил J – число безрозмірне, то витратна характеристика К повинна мати розмірність витрати рідини. З рівняння (12) виходить, що витратна характеристика є витратою рідини в трубі заданого діаметру при гідравлічному ухилі, рівному одиниці.

Якщо розхідну характеристику виразити через діаметр труби, то, памятаючи, що показник ступеня у формулі Н.Н. Павловського залежить від гідравлічного радіусу R і коефіцієнта шорсткості п : y=f (n, R), або y = fl (n, d) укладаємо наступне: при п = const витратна характеристика є тільки функцією діаметра труби: .

Показник ступеня y визначався по повній формулі Н.Н. Павловського при коефіцієнті шорсткості п = 0,012.

Дані значення величини

,

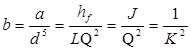які також необхідні при гідравлічних розрахунках трубопроводів.

Нарешті, звертаючись до раніше одержаної формули (6), введемо в неї вираз для витратної характеристики К .

Оскільки

,

то

.

Тоді

,

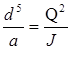або

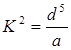. (13)

Підставивши залежність (13) в другу водопровідну формулу (6), одержимо

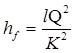, (14)

або

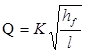. (15)

3 . Гідравлічний розрахунок простого довгого трубопроводу

Як наголошувалося раніше, місцевими втратами опору у разі довгих трубопроводів звичайно нехтують, іноді не враховують і швидкісний натиск, причому вважають, що напірна лінія практично співпадає з пєзометричною.

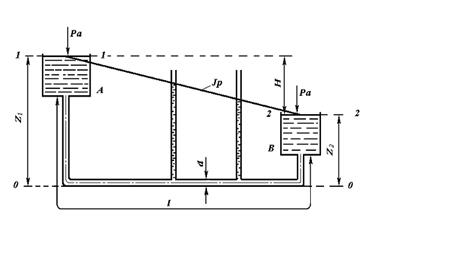
Мал. 2

Розглянемо умови сталого руху рідини по трубопроводу, що сполучає два резервуари А і В (мал. 6.2). Намітимо площину порівняння 0–0, як показано на кресленні. Напишемо рівняння Бернуллі для перерізів 1–1 і 2–2, співпадаючих з рівнями рідин в резервуарах А і В:

.

При значних площах живих перерізів потоку в резервуарах швидкості в цих перерізах будуть малі, а різниця близька до нуля. Тоді .

Отже, різниця рівнів Н в двох даних резервуарах повністю витрачається на подолання опорів в трубопроводі.

Таке положення має місце за наявності резервуару В (коли закінчення рідини виходить під рівень). У разі ж закінчення рідини з трубопроводу в атмосферу одержуємо дещо іншу картину.

Якщо простий трубопровід складається з труб різного діаметру (мал. 3), то в цьому випадку загальна втрата опору h_f розділяється нерівномірно по довжині трубопроводу, а пєзометрична лінія є суцільною ламаною лінією.

Застосуємо залежність (14) до розрахунку простого трубопроводу з послідовним зєднанням труб різного діаметру (мал. 3).

Причому швидкісним натиском 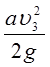нехтуватимемо. Діаметри труб і довжини окремих ділянок відомі.

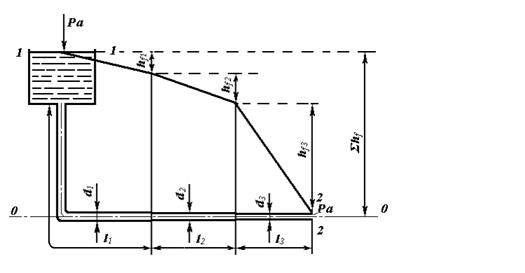
Мал. 3

Отже, ми можемо визначити їх витратні характеристики. Напишемо для кожної ділянки трубопроводу рівності

; ;.

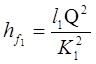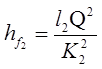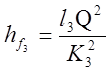де h_f1 , h_f2 , h_f3 – втрати опору по довжині на ділянці трубопроводу з довжинами l₁ , l₂ , l₃ , діаметрами d₁ , d₂ , d₃ і витратними характеристиками К₁ , К₂ , К₃ .

Загальні втрати опору по довжині трубопроводу рівні сумі втрат опору на окремих його ділянках: h_f = h_f1 + h_f2 + h_f3 або

,

,

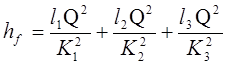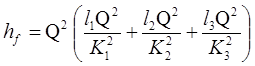звідки

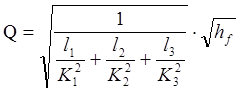. (16)

Позначивши постійну величину, що характеризує пропускну спроможність даного трубопроводу, через

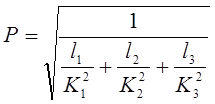
остаточно одержимо

, (17)

або

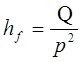. (18)

Для побудови пєзометричної лінії у разі даного трубопроводу необхідно обчислити значення втрат опору hf₁ , hf₂ і hf₃ і відкласти їх у відповідному масштабі на кресленні.

Приклад 1

Вода з водонапірної башти подається до вагоноремонтного заводу по трубопроводу завдовжки l = 3,5 км , діаметром d = 300 мм . Визначити витрату води, якщо відмітка землі в місці установки башти z = 130 м , відстань від землі до рівня води в башті Н = 17 м , відмітка землі біля заводу z₃ = 110 м, потрібний натиск води біля заводу Нсв = 25 м .

По таблиці для п = 0,012 і d = 300 мм знаходимо витратну характеристику К = 1,121 м³ /сек. Витрату визначимо по формулі (15):

Q0,0656м³ /сек.= =65,6 л/сек.

Приклад 2

Визначити для умов прикладу 1 висоту башти (відстань від землі до рівня води в резервуарі), яка зможе забезпечити подачу води на завод в кількості Q = 85 л/сек.

Визначимо втрату опору по формулі (14):

= 20,1 м .

Потім знайдемо висоту башти:

Н_б = z₃ + Н_СВ + h_f – z_б = 110 + 25 – 20,1 – 130 = 25,1 м.

Приклад 3

Рівень води у водонапірній башті на h_f – 25 м перевищує рівень води в точці її споживання. Довжина трубопроводу l = 2400 м . Підібрати діаметр трубопроводу при витраті води Q = 35 л/сек .

Обчислимо значення величини b :

/ (м³ /сек)²

По таблиці визначаємо два найближчі значення величини b:

при d = 150 мм b = 31,18/ (м³ /сек)²

при d = 200» b = 6,78

Для того, щоб трубопровід забезпечив подачу заданої витрати води, необхідно прийняти найближче більше значення діаметру d = 200 мм.

Приклад 4

Вода подається по трубопроводу, складеному з послідовно сполучених труб різних довжин і діаметрів: l ₁ = 700 м, l ₂ = 500 м, l ₃ = 200 м, d₁ – 300 мм, d₂ = 250 мм, d₃ = 200 мм. Визначити втрати опору в трубопроводі при витраті води Q = 45 л/сек.

Для визначення втрати опору скористаємося залежністю (16);

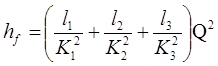
По таблиці для n = 0,012 знаходимо витратні характеристики для відповідних діаметрів: К₁ = 1,12 м³ /сек , К₂ – 0,692 м³ /сек і К₃ = 0,384 м³ /сек .

Тоді

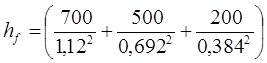0,0452 = 5,98 м .

4 . Гідравлічний розрахунок коротких трубопроводів

При гідравлічному розрахунку коротких трубопроводів враховуються як втрати опору по довжині, так і місцеві втрати опору. Якщо місцеві опори розташовані один від одного на відстані не менше 20 діаметрів труби, то в цьому випадку коефіцієнт опору даного місцевого опору практично не залежить від сусідніх опорів. Для визначення загальних втрат опору необхідно встановити коефіцієнт опору системи _сист = ..

При гідравлічному розрахунку коротких трубопроводів постійного діаметру можуть зустрітися наступні основні задачі:

1) відомі діаметр і витрата рідини в трубопроводі, а також типи місцевих опорів, вимагається визначити втрати опору;

2) відомі діаметр трубопроводу і втрати опору в ньому, вимагається визначити витрату рідини в трубопроводі;

3) вимагається визначити діаметр трубопроводу для пропуску заданої витрати при відомих втратах опору.

Перші дві задачі можна вирішити безпосередньо по формулах:

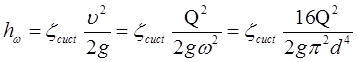(22)

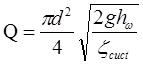
Третя задача розвязується підбором, оскільки коефіцієнт опору системи також є складною функцією від діаметру труби, визначення якого є мета задачі. В цьомувипадку слід будувати графік і по ньому знаходити діаметр, що відповідає рівності .Якщо втратамипо довжині можна нехтувати і жоден з коефіцієнтів, що враховують місцеві опори, не залежить від діаметру труби, то діаметр трубопроводу визначається безпосередньо по формулі

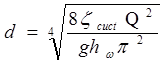. (23)

Цією ж формулою можна користуватися при рішенні задачі шляхом підбору. Заздалегідь визначається діаметр трубопроводу без врахування втрат опору по довжині. По цьому діаметру уточнюється коефіцієнт опору системи. Потім значення сист підставляється у формулу (23) і обчислюється уточнений діаметр трубопроводу.

Коли місцеві опори в трубопроводі розташовані на відстані менше 20d один від одного, то внаслідок відсутності інших прийомів розрахунку, що враховують взаємний вплив місцевих опорів, доводиться нехтувати цим впливом; при цьому розуміється, такий розрахунок носитиме тільки наближений характер.

Розрахунок сифона.

Сифон є коротким трубопроводом, по якому рідина рухається з живлячого резервуару А в приймальний В . Особливістю сифона є його здатність піднімати рідину на висоту Z над рівнем її в живлячому резервуарі. Принцип дії сифона заснований на утворенні вакууму в підвищеній частині сифона (в районі перерізу 2–2, що створює різницю тиску між атмосферним тиском, діючим на поверхню рідини в живлячому резервуарі А , і зниженим тиском в області вакууму в перерізі 2–2. Для того, щоб сифон почав діяти, треба заздалегідь заповнити його рідиною (наприклад, за допомогою спеціального насосу – вакууму).

Розрахунок сифона полягає у визначенні його пропускноїздатності і граничного значення висоти Z, при якій сифон може ще працювати. Розрахунок пропускної спроможності сифонів проводиться по формулі

Q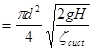

де через Н позначена різниця рівнів рідини в резервуарах А і В , а через – сумарний коефіцієнт опору трубопроводу.

Для розрахунку висоти Z припустимо, що резервуари А і В сполучені сифоновим трубопроводом. Напишемо рівняння Бернуллі для перерізів 1–1 і 2–2 щодо площини порівняння 0–0, співпадаючої з рівнем води в живлячому резервуарі A :

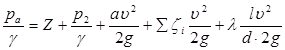
тут p ₂ – гідродинамічний тиск в перерізі 2–2;

– середня швидкість руху рідини в трубі;

Z – відстань від рівня рідини в резервуарі А доцентру труби в перерізі 2–2;

_і – сума коефіцієнтів місцевих опорів трубопроводу між перерізми 1–1 і 2–2. Оскільки

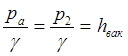
то

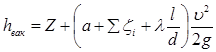(25)

і

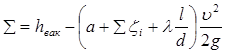. (26)

Оскільки граничне значення вакууму складає приблизно 10 м вод. ст., то, враховуючи наявність втрат опору в сифоні, а також неможливість великого пониження тиску в ньому, щоб уникнути кавітації висоту Z звичайно приймають не більше 7–8 м.

Скачать архив с текстом документа