Генерирование коррелированных случайных процессов в среде LabVIEW
СОДЕРЖАНИЕ: Разработка прикладного программного обеспечения для организации взаимодействия с измерительной и управляющей аппаратурой с помощью LabVIEW. Генерирование коррелированных случайных процессов и последовательностей, применение рекурсивного фильтра.Введение
LabVIEW (LaboratoryVirtualInstrumentEngineeringWorkbench) позволяет разрабатывать прикладное программное обеспечение для организации взаимодействия с измерительной и управляющей аппаратурой, сбора, обработки и отображения информации и результатов расчетов, а также моделирования как отдельных объектов, так и автоматизированных систем в целом. Разработчиком LabVIEW является американская компания National Instruments.
В отличие от текстовых языков, таких как C, Pascal и др., где программы составляются в виде строк текста, в LabVIEW программы создаются в виде графических диаграмм, подобных обычным блок-схемам. Иногда можно создать приложение, вообще не прикасаясь к клавиатуре компьютера.
LabVIEW является открытой системой программирования и имеет встроенную поддержку всех применяемых в настоящее время программных интерфейсов, таких как Win32 DLL, COM.NET, DDE, сетевых протоколов на базе IP, DataSocket и др. В состав LabVIEW входят библиотеки управления различными аппаратными средствами и интерфейсами, такими как PCI, CompactPCI/PXI, VME, VXI, GPIB (КОП), PLC, VISA, системами технического зрения и др. Программные продукты, созданные с использованием LabVIEW, могут быть дополнены фрагментами, азработанными на традиционных языках программирования, например C/С++, Pascal, Basic, FORTRAN. И наоборот можно использовать модули, разработанные в LabVIEW в проектах, создаваемых в других системах программирования. Таким образом, LabVIEW позволяет разрабатывать практически любые приложения, взаимодействующие с любыми видами аппаратных средств, поддерживаемых операционной системой компьютера.
1. Генерирование коррелированных случайных процессов
N-мерная плотность распределения вероятности wN (x1 , x2 , …xN ) связывает каждый отсчет случайной последовательности со всеми остальными отсчетами. Такое описание очень сложно и на практике используются более простые модели случайного процесса с зависимыми отсчетами. Наиболее известны две: марковская модель и спектрально-корреляционная модель. В марковской модели каждый отсчет случайного процесса зависит только от одного предыдущего (марковский процесс первого порядка). Для него N-мерная плотность распределения вероятности
wN (x1 , x2 , … xN ) = w(x1 )w(x2 /x1 ) w(x3 /,x2 )*…* w(xN / xN - 1 ) = w(x1 )w(xi /xi – 1 ).
Марковский процесс не является чисто теоретическим допущением, таким будет процесс на выходе интегрирующей цепи при подаче на ее вход белого шума.
Спектрально-корреляционная модель оперирует с двумерной плотностью распределения вероятности w(x1 , x2 ), связывающей отсчеты случайного процесса, взятые в разные моменты времени x1 = x(t1 ) и x2 = x(t2 ). Если изменять t1 и t2 , то можно исследовать попарную связь всех отсчетов между собой и, в принципе, последовательно определить все связи, описываемые N-мерным законом распределения. В спектрально-корреляционной модели для описания этой связи используется корреляционный (второй смешанный центральный) момент:
![]()
Стационарные случайные процессы характеризуются неизменностью характеристик во времени, и для таких процессов корреляционный момент не зависит от выбора начального момента времени t1 , а определяется только величиной интервала = t2 – t1 .
Зависимость корреляционного момента от временного интервала между отсчетами называется корреляционной функцией R() случайного процесса. При = 0 значение корреляционной функции максимально и равно дисперсии случайного процесса 2 . С увеличением || корреляционная функция уменьшается до нуля монотонно или по колебательному закону.При моделировании всегда используется реализация случайного процесса конечной длины и в измеренной корреляционной функции появляются нескомпенсированные остатки. Уровень этих остатков тем меньше, чем больше длина реализации. На рис. 1 показаны корреляционные функции для случайной последовательности с треугольной функцией корреляции для количества отсчетов последовательности, равным 100 (рис. 1, а) и 10000 (рис. 1.б).
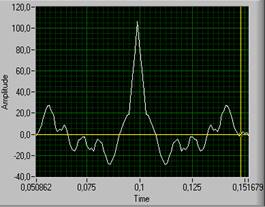 |
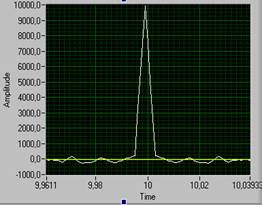 |
| а) | б) |
Рис. 1
Случайный процесс называется некоррелированным, если корреляционная функция равна нулю для любого , отличного от нуля. Для некоррелированного процесса R() = 2 к (), где к () – символ Кронекера: он равен 1 при = 0 и нулю при всех других . Вообще говоря, некоррелированность не означает независимости. Это можно пояснить следующим примером.
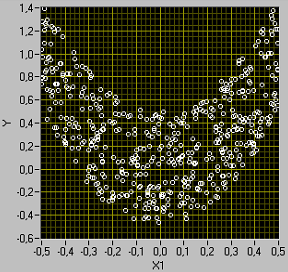
Рис. 2
Пусть случайная величина Y = 4X1 2 + X2 , где X1 и X2 – независимые случайные величины, равномерно распределенные в интервале (– 1/2, 1/2). Ясно, что Y связана с X1 статистической зависимостью (см. рис. 2). Однако корреляционный момент
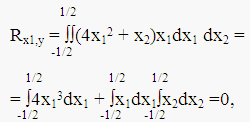
так как каждый из интегралов является интегралом от нечетной функции в симметричных пределах.
Рассмотренная статистическая связь является нелинейной и никак не отражается в корреляционной функции. Корреляционная функция характеризует только линейную статистическую зависимость между отсчетами случайного процесса.
Для измерения корреляционной функции в LabVIEW существует несколько виртуальных приборов. В данной работе используется экспресс-ВП ConvolutionandCorrelation (Свертка и корреляция) (рис. 3 а), так как он представляет собой завершенную программу, не требует никаких дополнительных узлов управления и удобен в использовании. Панель конфигурирования экспресс-ВП ConvolutionandCorrelation показана на рис. 3, б).
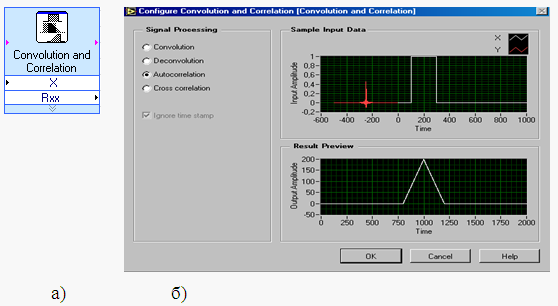
Рис. 3
Корреляционная функция связана с энергетическим спектром случайного процесса преобразованием Винера-Хинчина, которое по форме совпадает с двусторонним преобразованием Фурье. Энергетический спектр случайной последовательности, содержащей N отсчетов, рассчитывается как двустороннее дискретное преобразование Фурье (ДПФ) от дискретной корреляционной функции R(n):
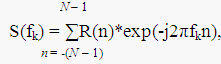
где fk = k/N*t – частота спектральной составляющей, t – временной интервал между соседними отсчетами случайного процесса, или интервал дискретизации.
Из приведенного выражения следует, что энергетический спектр случайной последовательности является дискретным и периодическим (рис. 4). Он содержит гармоники частоты f1 = 1/N*t. Это самая низкая частота спектра, так как за время, равное длительности случайной последовательности N*t, укладывается только один период колебания этой частоты.
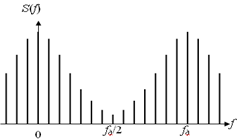
Рис. 4
|
LabVIEW располагает разнообразными ВП для спектрального анализа (более 20 типов). Воспользуемся экспресс-ВП SpectralMeasurements (Рис. 5), в котором предусмотрена возможность усреднения (Averaging) и оконной обработки (Window) для уменьшения краевых эффектов.

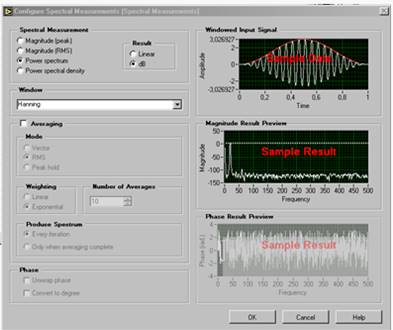
а) б)
Рис. 5
2. Генерирование коррелированных случайных последовательностей
Чаще всего для генерирования коррелированных случайных последовательностей используется метод формирующего фильтра. Если на вход линейного формирующего фильтра подать белый шум x(t), то на его выходе будет коррелированный случайный процесс y(t) с корреляционной функцией, определяемой характеристиками фильтра. Энергетический спектр случайного процесса связан с частотной характеристикой фильтра соотношением:
Sy () = x 2 |K(j)|2 , ( 1)
а корреляционная функция определяется импульсной характеристикой фильтра.
Задача определения характеристик фильтра по заданной корреляционной функции (задача синтеза) достаточно сложна, поэтому в лабораторной работе мы остановимся только на вопросах реализации фильтров и оценки влияния параметров фильтра на форму корреляционной функции.
Метод скользящего суммирования В методе скользящего суммирования (скользящего среднего) выходной процесс определяется как весовая сумма отсчетов входного процесса, взятых в настоящий t = nt и предшествующие моменты времени:
y(nt) = b0 x(nt) + b1 x(nt – t) + b2 x(nt – 2t) + … + bk x(nt – kt). ( 2)
В следующий момент времени t = nt + t
y(nt + t) =
= b0 x(nt +t) + b1 x(nt) + b2 x(nt – t) + … + bk x(nt – (k – 1) t)
и т.д. для последующих моментов времени.
Значения корреляционной функции выходного процесса определятся как математическое ожидание произведения отсчетов выходного процесса, отстоящих друг от друга на интервал it.
Ry (it) = M{ y(nt)y(nt +it)}.
Учитывая, что входной процесс не коррелирован и, следовательно,
M{ x(nt)x(nt +it)} = x 2 к (it),
Получим
Ry (0) = y 2 = (b0 2 + b1 2 + b2 2 + … + bk 2 )x 2 ,
Ry (t) = (b0 b1 + b1 b2 + b2 b3 + … + bk – 1 bk )x 2 ,
Ry (2t) = (b0 b2 + b1 b3 + … + br – 2 bk )x 2 ,
Ry (kt) = b0 bk x 2 ,
Ry (kt + t) = 0.
Эти уравнения позволяют легко решить задачу анализа: рассчитать корреляционную функцию по известным коэффициентам bi . Задача синтеза: найти коэффициенты фильтра bi по заданной корреляционной функции в общем случае не решена. Но для треугольной корреляционной функции решение находится просто: все коэффициенты bi одинаковы:
bi = (y 2 /x 2 )/k.
Если потребовать, чтобы дисперсии входного и выходного процессов были равными, то
bi = 1/k. ( 3)
Схема фильтра, построенного по выражению ( 2), приведена на рис. 6. Символ z-1 означает задержку на интервал дискретизации. Фильтр скользящего суммирования (СС-фильтр) является фильтром с конечной импульсной характеристикой (КИХ-фильтром) или нерекурсивным (трансверсальным) фильтром.
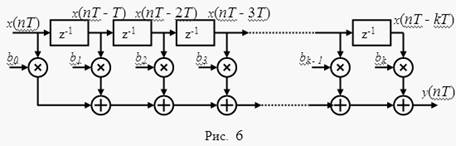
Изображенный фильтр описывается системной (передаточной) функцией
K(z-1 ) = b0 + b1 z-1 + b2 z-2 + … + bk z-k .
Передаточная функция в стандартной форме, полученная из системной функции умножением числителя и знаменателя на zk , имеет вид:
K(z) = (b0 zk + b1 zk - ! + … + bk )/zk .
Недостаток СС-фильтра: увеличение порядка фильтра с увеличением количества отсчетов корреляционной функции. Если корреляционная функция имеет бесконечную протяженность, то для сокращения порядка фильтра ее искусственно ограничивают по времени, пренебрегая малыми значениями корреляционной функции. Это приводит к возникновению методической ошибки моделирования.
Авторегрессионный метод Существенная экономия машинных ресурсов и возможность моделирования случайных процессов с корреляционной функцией бесконечной протяженности достигается при использовании авторегрессионного метода. Авторегрессионный метод предполагает использование рекурсивных фильтров с системной функцией
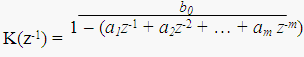
где m – порядок фильтра.
Как следует из вида системной функции, выходной процесс авторегрессионного фильтра (АР-фильтра) связан с входным процессом рекуррентным соотношением
y(nT) =b0 x(nT) + a1 y(nT – T) + a2 y(nT – 2T) + … + am y(nT – mT).
Корреляционная функция определяется коэффициентами ai . Непосредственно по этому выражению нельзя найти корреляционную функцию, зная коэффициенты ai , как это было сделано по выражению (2). Для выявления качественного влияния коэффициентов на форму корреляционной функции воспользуемся ее связью с импульсной характеристикой фильтра. Рассмотрим сначала АР-фильтр первого порядка (рис. 7).
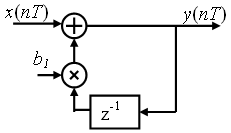
Рис. 7
Его передаточная функция в стандартной форме
K(z) =![]() .
.
Импульсная характеристика определяется как обратное Z – преобразование от передаточной функции:
g[n] = b0 a1 n ( 4)
Диапазон возможных значений коэффициента a1 ограничивается устойчивостью фильтра. Для устойчивости АР-фильтра требуется, чтобы полюса его передаточной функции находились внутри окружности единичного радиуса.
Полюс находится приравниванием нулю знаменателя передаточной функции:
z – a1 =0.
Полюс
z1 = a1 ,
и требование устойчивости фильтра
| a1 | 1 или -1 a1 1.
При положительном a1 импульсная характеристика, как следует из ( 4), является монотонно спадающей функцией, и корреляционная функция тоже будет монотонно спадающей. При отрицательном а1 импульсная характеристика становится колебательной, и корреляционная функция будет колебательной затухающей с периодом колебаний равным двум интервалам дискретизации.
Рассмотрим, как будет изменяться АЧХ фильтра, а следовательно, и энергетический спектр ( 1) генерируемой последовательности, при изменении а1 . Комплексная частотная характеристика получается из передаточной функции К(z) подстановкой z = ejt . Амплитудно-частотная характеристика
К() = |b0 ejt /(ejt – a1 )| = b0 /|ejt – a1 |.
Она обратно пропорциональна модулю разности векторов ejt и a1 . Как видно из рис. 8 а), при положительном a1 модуль разности векторов будет изменяться от наименьшего значения при = 0 до наибольшего значения при t = . Значит, АЧХ, а следовательно, и энергетический спектр случайной последовательности, будет иметь подъем в области низких частот. При отрицательных a1 , наоборот, подъем будет в области верхних частот.
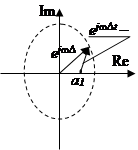 |
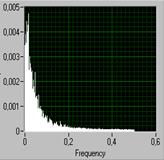 |
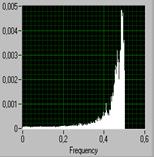 |
| а) | б) | в) |
| Рис. 8 |
На рис. 8, б) показан энергетический спектр процесса на выходе фильтра при a1 = 0,8; а на рис. 8, в) – при a1 = - 0,8.
АР-фильтр второго порядка позволяет формировать коррелированные последовательности с более разнообразными корреляционными функциями. Его системная функция
K(z-1
) = ![]() .
.
Значения коэффициентов а1 и а2 ограничены областью устойчивости, которая показана на рис. 9 (коэффициенты должны находиться внутри треугольника).Область устойчивости делится на четыре подобласти в зависимости от вида полюсов: А – два действительных полюса разного знака; В – два действительных отрицательных полюса; С – два действительных положительных полюса; D – два комплексно сопряженных полюса. От расположения полюсов будет зависеть форма энергетического спектра и корреляционной функции генерируемого случайного процесса.
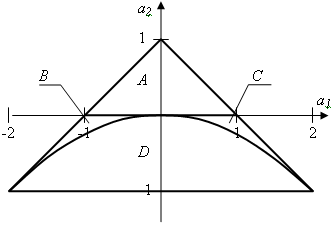
Рис. 9
Эту зависимость для действительных корней мы уже обсуждали. Для комплексно-сопряженных полюсов подъем АЧХ будет на частоте
f = (fд /2)(argz1 /),
где argz1 – аргумент полюса, расположенного в верхней полуплоскости.
АР-фильтр является рекурсивным фильтром, или фильтром с бесконечной импульсной характеристикой (БИХ-фильтром). Последовательное соединение СС-фильтра и АР-фильтра называют АРСС-фильтром. Его системная функция записывается в виде отношения двух полиномов:
K(z-1
) = ![]()
Такой фильтр обладает еще большими возможностями генерирования коррелированных процессов с разнообразными корреляционными функциями. Для моделирования СС- и АР- фильтров в среде LabVIEW удобно использовать ВП IIRFilter (БИХ-фильтр) (рис. 10).
Он производит фильтрацию входной последовательности Х.
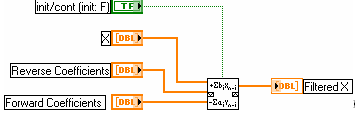
Рис. 10
Выходная последовательность (FilteredX) вычисляется по выражению
y(n) = b0 x(n) + b1 x(n – 1) + … + bk x(n – k) –
– (a1 y(n – 1) + a2 y(n – 2) + … + am y(n – m)).
Системная функция фильтра:
K(z-1
) = ![]()
Она отличается от записанной ранее системной функции АРСС-фильтра знаком коэффициентов ai (i 1).Коэффициенты числителя задаются в виде одномерного массива и подаются на терминал ForwardCoefficients. Массив коэффициентов знаменателя подается на терминал ReverseCoefficients.
Логическая переменная, подаваемая на вход init/cont (init: F) (инициировать/продолжить (иниц: F)) управляет инициализацией внутренних состояний фильтра. По умолчанию на входе установлено значение ЛОЖЬ. При этом внутренние состояния устанавливаются в 0. При установке на входе инициировать/продолжить значения ИСТИНА внутренние состояния соответствуют последним состояниям фильтра из предыдущего запуска ВП. При нулевых внутренних состояниях выходной процесс устанавливается в стационарное состояние спустя некоторое время после запуска ВП (время переходного процесса). Для устранения переходного процесса целесообразно установить логическую переменную в состояние ИСТИНА и обеспечить повторный запуск. Последняя генерируемая последовательность будет стационарной.
Для многократного повторения моделирования целесообразно использовать структуру WhileLoop (Цикл по условию). Он эквивалентен выражению: do (программа) while (логическое условие). Цикл While похож на цикл For. Различие этих циклов в том, что число итераций в цикле For заранее определено и задается через терминал N числа итераций, а в цикле While – итерации продолжаются, пока не будет выполнено заданное условие.

Рис. 11
Внутри структуры While (рис. 11) размещаются терминал счетчика итераций ![]() и терминал условия выхода из цикла
и терминал условия выхода из цикла ![]() . Программа, размещенная в структуре, выполняется до подачи на терминал условия выхода из цикла логической переменной TRUE.
. Программа, размещенная в структуре, выполняется до подачи на терминал условия выхода из цикла логической переменной TRUE.
измерительный программный рекурсивный фильтр
Заключение
LabVIEW (Laboratory Virtual Instrumentation Engineering Workbench) — это среда разработки и платформа для выполнения программ, созданных на графическом языке программирования «G» фирмы National Instruments (США). Первая версия LabVIEW была выпущена в 1986 году для Apple Macintosh, в настоящее существуют версии для UNIX, GNU/Linux, Mac OS и пр., а наиболее развитыми и популярными являются версии для Microsoft Windows.
LabVIEW используется в системах сбора и обработки данных, а также для управления техническими объектами и технологическими процессами. Идеологически LabVIEW очень близка к SCADA-системам, но в отличие от них в большей степени ориентирована на решение задач не столько в области АСУ ТП, сколько в области АСНИ.
Список литературы
1. Н.А. Виноградова, Я.И. Листратов, Е.В. Свиридов. «Разработка прикладного программного обеспечения в среде LabVIEW». Учебное пособие – М.: Издательство МЭИ, 2005.
2. http://www.automationlabs.ru/
3. http://digital.ni.com/
4. http://www.labview.ru/
5. http://ru.wikipedia.org/