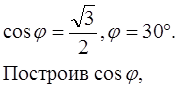Геометрические построения на плоскости

СОДЕРЖАНИЕ: Общие аксиомы конструктивной геометрии. Аксиомы математических инструментов. Постановка задачи на построение, методика решения задач. Особенности методик построения: одним циркулем, одной линейкой, двусторонней линейкой, построения с помощью прямого угла.

Введение

Вам, будущим учителям, в школьном курсе математики придется учить ребят решению задач на построение. Целесообразность этой деятельности обусловлена тем, что задачи на построение развивают конструктивное и логическое мышление, прививают навыки исследователя. Поэтому эти задачи составляют важную часть школьного курса геометрии.

Общие аксиомы конструктивной геометрии. Аксиомы математических инструментов

Раздел геометрии, в котором изучаются геометрические построения, называется конструктивной геометрией.

Основным понятием конструктивной геометрии является понятие построить геометрическую фигуру.

Это понятие принимается без определения, конкретный его смысл известен из практики, где оно означает: начертить, провести (линию), отметить (точку). В интересах логической строгости изложения основное понятие конструктивной геометрии - построить фигуру - характеризуется через основные требования (общие аксиомы конструктивной геометрии).

Эти требования обычно не формулируются в пределах школьного курса геометрии, но они подразумеваются в процессе решения любой геометрической задачи на построение как нечто само собою разумеющееся. Общие аксиомы конструктивной геометрии выражают в aабстрактной форме наиболее существенные моменты многовековой чертежной практики и составляют логическую основу конструктивной геометрии.

Рассмотрим эти общие аксиомы теории геометрии.

I. Каждая данная фигура построена, т.у. если о какой-либо фигуре сказано, что она дана, то под этим подразумевается, что она уже изображена, начерчена, по-другому говоря, построена.

2. Если даны две фигуры, то построено:

а) их объединение

б) пересечение (если оно непусто )

в) разность (если она не равна пустому множеству)

3. Если дана некоторая фигуpa, то можно построить точку:

а) принадлежащую данной фигуре

б) не принадлежащую ей.

Замечание . Аксиомы За и 3б дают возможность построить новые точки, но этим точкам не приписывают никаких свойств. Для построения новых точек, обладающих определенными свойствами, пользуются математическими инструментами: линейкой, циркулем, углом и т.д. Свойства указанных математических инструментов описываются с помощью соответствующих аксиом. При этом следует четко видеть разницу между математическим инструментом конструктивной геометрии и их физическим олицетворением.

Аксиома линейки . Линейка (односторонняя) позволяет построить прямую, проходящую через две данные точки.

Аксиома циркуля . Циркуль позволяет построить окружность с центром в данной точке и радиусом, равным длине данного отрезка.

Аксиомы двусторонней линейки . Двусторонняя линейка позволяет: а) выполнить любое построение, выполнимое линейкой;

б) в каждой из полуплоскостей, определяемых построенной прямой, построить прямую, параллельную этой прямой и проходящую от нее на расстоянии h, где h - фиксированный элемент для данной двусторонней линейки (ширина);

в) если построены две точки А и В, то установить, будет ли АВ h, и если AB h , то построить 2 пары параллельных прямых, проходящих соответственно через А и В и отстоящих одна от другой на расстоянии h ,

Аксиомы угла . Угол позволяет: а) сделать все построения, выполнимые линейкой; б) через данную точку плоскости провести под углом к некоторой данной прямой; в) если построены отрезок АВ и фигура ф , то установить, содержит ли фигура Ф точку, из которой отрезок АВ виден под углом , и если такая существует, то построить ее.

Постановка задачи на построение

Задача на построение состоит, в том, что требуется построить указанными инструментами фигуру, если дана некоторая другая фигура и указаны некоторые соотношения между элементами искомой фигуры и данной.

Каждая фигура, удовлетворяющая условию задачи, называется решением задач.

Построения, о возможности которых оказано в аксиоме 3, вместе с построениями, перечисленными в аксиомах математических инструментов, назовем основными построениями (ОП).

Найти решение задачи на построение - значит указать конечную последовательность основных построений, после выполнения которых искомая фигура будет считаться построенной в силу принятых аксиом конструктивной геометрии.

Перечень основных построений, а следовательно, и ход решения задачи, зависит от употребляемого набора инструментов. Следует заметить, что такой подход в определении нахождения решения не рациональный. Иногда целесообразнее укрупнить шаги построения.

Рассматривают как шаг построения целые блоки основных построений. Эти блоки представляют собой решения элементарных задач на построение. Их назовем элементарными построениями. Тогда можно дать следующее определение.

Решить задачу на построение - это значит указать такую конечную последовательность основных (ОП) и элементарных построений (ЭП), после выполнения которых искомая фигура может считаться построенной в силу общих аксиом конструктивной геометрий.

В качестве элементарных построений (ЭП) возьмем следующие задачи.

ЭП I. Отложить на данном луче от его начала отрезок, равный данному отрезку.

ЭП 2. Отложить от данного луча в данную полуплоскость угол, равный данному углу.

ЭП 3. Построить треугольник по трем сторонам.

ЭП 4. Построить треугольник по двум сторонам и углу между ними.

ЭП 5. Построить треугольник по стороне и двум прилежащим углам.

ЭП 6. Построить биссектрису данного неразвернутого угла.

ЭП 7. Построить серединный перпендикуляр данного отрезка.

ЭП 8. Построить середину данного отрезка.

ЭП 9. Построить прямую, проходящую через данную точку и перпендикулярную данной прямой. (При этом данная точка может лежать на данной прямой, может и не лежать на ней).

ЭП 10. Построить прямую, проходящую через данную точку и параллельную данной прямой.

ЭП 11. Построить прямоугольный треугольник по гипотенузе.

ЭП 12. Построить прямоугольный треугольник по гипотенузе и катету.

ЭП 13. Построить касательную к окружности, проходящую через данную на ней точку.

Иногда условиям задачи на построение удовлетворяют несколько фигур.

Решить задачу на построение - значит найти все ее решения. Поясним это определение.

Фигуры, удовлетворяющие условию задачи, могут отличаться размерами, формой и положением на плоскости. Фигуры, удовлетворяющие условию задачи, отличающиеся размерами или формой, будем считать различными. С расположением дело обстоит так.

Если условие задачи не предусматривает определенного расположения искомой фигуры относительно данных фигур, то задача считается решенной, если: а) построено некоторое число неравных фигур Ф₁ ,…, Ф₂ удовлетворяющих условию задачи, и б) доказано, что всякая фигура, удовлетворяющая условию задачи, равна одной из них; считается, что задача имеет n решений (о точностью до равенства).

Если условие задачи предусматривает определенное расположение искомой фигуры относительно какой-либо данной фигуры, то задача считается решенной, если: а) построено некоторое число фигур, удовлетворяющих условию задачи, и б) доказано, что любая фигура, удовлетворяющая условию задачи, совпадает с одной из них. При этом равные фигуры, но различно расположенные, считаются различными решениями. Приведем примеры.

Пример 1 . Построить циркулем и линейкой треугольник по трем сторонам. Точный смысл: построить треугольник так, чтобы три его стороны были равны трем данным отрезкам. Условие задачи не предусматривает определенного расположения искомой фигуры относительно данных фигур.

По нашей договоренности решение такой задачи ищется с точностью до равенства. Так как все треугольники по трем сторонам равны, то задача имеет одно решение, если сумма любых двух сторон больше третьей, и не имеет решения, если это условие не выполнено.

Пример 2. Построить циркулем и линейкой треугольник так, чтобы одной его стороной служил данный отрезок АВ , а две другие его стороны были равны двум данным отрезкам а и в.

В этом случае условие задачи предусматривает определенное расположение искомого АВС относительно данных фигур. В соответствии с нашим соглашением равные треугольники, удовлетворяющие условию задачи, но отличающиеся расположением, будем считать разными решениями этой задачи.

а в

Замечание . Встречаются задачи, имеющие бесконечное множество решений. Такие задачи называются неопределенными. Очевидно, все решения нельзя построить. В связи с этим вопросом: когда же считать неопределенную задачу решенной?

Решение неопределенной задачи ищется в параметрической форме: указывается прием построения фигур, удовлетворяющих условию задачи, причем эти фигуры определяются выбором определенного положения одной точки на некоторой данной фигуре. Эти точки играют роль геометрического параметра. Задача считается решенной, если при всевозможных допустимых положениях произвольной точки возникают все фигуры, удовлетворяющие условию задачи.

Встречаются задачи такие, что не существуют фигура удовлетворяющие условию задачи. Например, в параллелограмм (не ромб) нельзя вписать окружность. Нельзя провести прямую через 2 данные точки одним лишь циркулем.

Во всех этих случаях решить задачу на построение - значит доказать, что искомая фигура не существует, или доказать, что она не может быть построена данными средствами.

Условие задачи часто дает известный простор в выборе данных. Например, если требуется построить треугольник по трем сторонам, то данными являются три отрезка, которые могут быть произвольными по величине и положению. Задача в такой формулировке считается решенной, если она решена для всех принципиально различных предположений относительно выбора данных.

Может оказаться, что при таком выборе данных задача решается иначе, чем при другом их выборе, поэтому приходится рассматривать ряд отдельных случаев и давать решение задачи для каждого из них.

Методика решения задач на построение

При решении сложных задач основную трудность представляет вопрос о том, как найти способ решения. Решение этого вопроса облегчается, если придерживаться определенной схемы рассуждений. Эта схема состоит их четырех этапов: анализ, построение, доказательство, исследование. Заметим, что эта классическая схема не является, безусловно, необходимой и неизменной. Допустимы отклонения в зависимости от задачи.

1. Анализ . В анализе ведется поиск решения задачи следующим образом: предполагают задачу решенной, строят (от руки) искомую фигуру пристраивают к ней данные с учетом тех отношений, которые указаны в условии задачи. Подмечают, что построение искомой фигуры Ф сводится к построению другой фигуры Ф₁ , построение Ф₁ сводят к построению Ф₂ и т.д. После конечного числа шагов можно прийти к некоторой фигуре Ф_n , построение которой известно.

Если на вспомогательном чертеже не удастся найти ход решения, то целесообразно ввеcти в чертеж вспомогательные фигуры: сделать дополнительные построения, сделать геометричеcкие преобразования и т.д.

2. Построение состоит в указании конечной последовательности основных построений (или ранее решенных задач), которые достаточно произвести, чтобы искомая фигура была построена.

Построение обычно сопровождается графическим оформлением каждого шага с помощью указанных инструментов.

3. Доказательство имеет целью установить, что построенная фигура действительно удовлетворяет условию задачи.

Доказательство проводится в предположении, что каждый шаг построения может быть выполнен.

4. Исследование . При анализе, построении обычно ограничиваются отысканием одного какого-либо решения, предполагая выполнимость шагов построения. Идя полного решения задачи нужно выяснить:

1) всегда ли (т.е. при любом ли выборе данных) можно выполнить построения избранным способом;

2) можно ли и как построить искомую фигуру, если для какого-нибудь выбора данных указанный способ построения не пригоден;

3) сколько решений имеет задача при каждом возможном выборе данных.

Эти вопросы составляют содержание исследования. Итак, исследование ставит цель - установить условия разрешимости и определить число решений.

Практически исследование проводят по ходу построения, рассматривая каждый шаг построения на возможность и единственность.

Однако такое исследование связано с данным способом построения. В этом случае остается открытым вопрос: нет ли других решений при другом способе решения. На этот вопрос отвечают с помощью указанного выше приема: доказывают, что произвольное решение данной задачи совпадает с одним из уже полученных решений.

Для иллюстрации сказанного рассмотрим следующий пример.

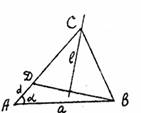
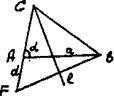
Задача . Построить треугольник, если известны: длина основания а, угол при основании и разность двух других сторон d.

Решение . Заметим, что в условии задачи не указаны инструменты. B таких случаях будем полагать (как и в школе), что задачу надо решить с помощью линейки и циркуля.

Анализ . Поиск решения задачи проведем, полагая задачу решенной. Пусть ABC - искомый треугольник: AB = a, AC–BC = AD=d, = . Замечаем, что АВD= определен по двум сторонам и углу между ними.

Третья вершина С искомого треугольника может быть найдена как точка пересечения луча АD и прямой l - серединного перпендикуляра отрезка ВD). Иначе говоря план решения найден, отроим треугольник АВD, а затем и третью вершину С.

Построение . В этом пункте реализуем план решения.

Строим последовательно:

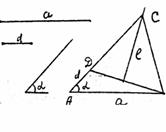
1)

2) l, l – серединный перпендикуляр отрезка BD;

3) C, C = [AD) l.

Треугольник АВС – искомый.

Доказательство . Действительно, АВС удовлетворяет всем условиям задачи, т.к. по построению

АВ = а, АС – ВС = АD = d, BAD = .

Исследование . Проверил каждый шаг построения на осуществимость и единственность. Первый шаг возможен и единственен тогда и только тогда, когда 0. Второй шаг возможен и единственен всегда. Третий шаг возможен и единственен тогда и только тогда, когда а cos . Действительно, если d acos , то прямая l пересекает луч AD. Если же d = acos , то l и AD, поэтому треугольника, удовлетворяющего условию задачи, не существует. В том случае, когда d acos , прямая l пересекает луч DА. В этом случае также задача не имеет решения.

Но вернемся к анализу. У нас задача решена, предполагая, что лежит против меньшей из двух боковых сторон. Если лежит против большей стороны, то предыдущий метод построения не проходит. Как быть? По теории мы должны и для этого случая дать решение. Нетрудно убедиться, что ABF определен (a,d и угол - ). Построение, доказательство и исследование провoдятcя так же, как и выше.

Необходимо еще выяснить: вcе ли решения найдены. Да, все, так как если бы каким-то способом построить треугольник по a, d и то этот треугольник был бы равен одному из указанных треугольников (это легко доказать через ).

Методы решения задач на построение

Основными являются три: метод геометрических мест (ГМТ), метод геометрических преобразований, алгебраический метод.

Метод геометрических мест (пересечения фигур).

Сущность метода : решение задачи сводит к построению некоторой точки (основного элемента построения), подчиненной двум условиям. Отбрасывают одно из этих условий и строят ГМТ Ф_{1 ,} удовлетворяющих первому условию, потом Ф₂ - ГМТ, удовлетворяющих второму условию. По соответствующей аксиоме конструктивной геометрии можем сказать Ф₁ Ф₂ = или нет и если , то считать построенным пересечение Ф₁ Ф₂ . Точки Ф₁ Ф₂ и только они удовлетворяют обоим условиям одновременно. Точки пересечения и только они дают решение задачи.

Заметим, что успех от применения этого метода полностью зависит от знания конкретных ГМТ. Наиболее часто применяются следующие геометрические места:

ГМТ 1. Множество точек плоскости, каждая из которых равноудалена от двух данных точек А и В, есть серединный перпендикуляр отрезка АВ.

ГMT 2. Множество точек, находящихся на данном расстоянии от данной прямой, есть две прямые, параллельные данной и отстоящие от нее на данном расстоянии.

ГМТ 3. Множество точек, каждая из которых равноудалена от двух данных параллельных прямых, есть прямая, являющаяся их осью симметрии.

ГМТ 4. Множество точек, каждая из которых равноудалена от двух пересекающихся прямых, есть две взаимно перпендикулярные прямые, содержащие биссектрисы углов, образованных данными прямыми,

ГМТ 5. Множества точек плоскости, из которых отрезок АВ виден под прямым углом, есть окружность (без точек А и В ), построенная на отрезке АВ как на диаметре.

ГМТ 6. Множество точек плоскости, из которых отрезок АВ виден под углом , где 90, 180 , есть две дуги с общими концами А и В (без точек А и В), симметричные относительно прямой АВ.

ГМТ 7. Множество точек плоскости, из которых данная окружность видна под углом , где , есть окружность,- концентрическая с данной, радиус которой больше радиуса данной окружности.

ГМТ 8. Множество точек, делящих всевозможные хорда окружности (O, ОА), проведенные через точку А окружности, в одном и том же отношении , где 0, есть окружность (без точки А) с центром на прямой ОА, проходящая через точку А. Если = 1, то эта окружность построена на отрезке ОА как на диаметре.

ГМТ 9. Множество точек плоскости, для каждой из которых разность квадратов расстояний от двух данных точек А и В постоянна, есть прямая, перпендикулярная прямой АB.

ГМТ 10. Множество точек плоскости, для каждой из которых сумма квадратов расстояний до двух данных точек А и В равна а² , есть окружность с центром в середине отрезка АВ, если 2а² AB² ; середина отрезка AB, если 2a² = AB² ; и пустое множество, если 2a² AB² .

ГМТ 11. Множество точек плоскости, для каждой из которых отношение расстояний до двух данных точек А и В постоянно и отлично от единицы, есть окружность с центром на прямой АВ (окружность Аполлония).

Для иллюстрации метода ГМТ решим следующую задачу.

Задача . Построить треугольник, если известны: длина основания а, угол при вершине и отношение боковых сторон , 1.

Решим методом ГМТ.

Анализ. Две вершины А и В искомого треугольника легко построить. Задача сводится к построению точки С. Точка С должна удовлетворять следующим двум условиям: 1) точка С принадлежит сегменту, вмещающему данный угол ; 2) точка С принадлежит окружности Аполлония.

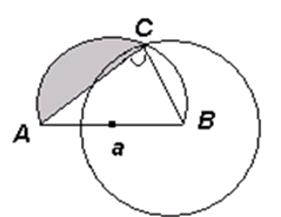
Построение. Строим последовательно: а) отрезок АВ, АВ = 0; б) сегмент А В, вмещающий данный угол ; в) окружность Аполлония на отрезке АВ; г) точку С , принадлежащую пересечению сегмента А В и окружности Аполлония.

Треугольник АВС - искомый.

Доказательство и исследование предлагаем читателям провести самостоятельно.

Метод геометрических преобразований

Сущность метода: при решении задачи, и прежде всего на первом этапе – анализе, наряду с данными и искомыми фигурами рассматривают другие фигуры, полученные из данных или искомых фигур (или их частей) с помощью некоторого геометрического преобразования (ГП). В зависимости от того, какое (ГП) выбрано, говорят о той или иной разновидности метода ГП (метод параллельного переноса, гомотетии, инверсии и т.д.). Рассмотрим примеры.

1. Параллельный перенос (ПП).

Сущность : наряду с данными и искомыми фигурами рассматривают другие фигуры, полученные из указанных фигур (или частей) с помощью ПП.

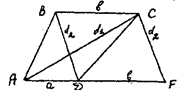
Задача. Достроить трапецию так, чтобы ее основания и диагонали были соответственно равны четырем данным отрезкам.

Анализ . Пусть ABCD - искомая трапеция. Сделаем параллельный перенос плоcкости, определяемый вектором ВС: ВС : BD CF.

Треугольник ACFопределен по трем сторонам: AF = a + b, AC = d₁ , CF = d₂ .

План решения ясен. Предлагаем читателям завершить решение этой задача.

2. Осевая симметрия.

Задача . Даны прямая l и две точки А и В, принадлежащие одной плоскости, определяемой прямой l. Найти такую точку Хl, чтобы сумма АХ + ХВ была минимальной.

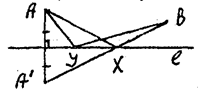
Уклонимся от схемы. Рассмотрим S_е . Пусть A = S_e (A), X = AB l. Покажем, что Х - искомая точка. В самом деле, для любой точки

Yl: AX + XB = AB AY + YB = AY + YB (Y X).

Исследование . Задача всегда имеет решение, причем единственное.

3. Поворот.

Задача . Даны: угол АОВ и точка С внутри него. Построить равносторонний треугольник, одна вершина которого совпадает о точкой С, а две другие лежат на сторонах данного угла.

Анализ . Пусть СDE - искомый. Сделаем поворот плоскости вокруг точки С на угол 60°: R⁶⁰ (D) = E, R⁶⁰ (OB) = OB, причем E = OB OB. Аналогично находим положение точки D: D = OB Rc^-60 (OA).

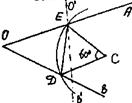
Построение очевидно. Доказательство и исследование предлагаем провести самостоятельно.

4. Центральная симметрия.

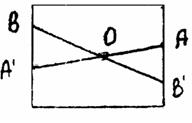
Задача. Построить квадрат, если даны его центр О и две точки А и В на параллельных его сторонах.

Анализ. Пусть искомый квадрат построен. Тогда А’ и В, где лежат на А’ = Z₀ (A), лежат на одной стороне квадрата. Аналогично В’ и А, где В = Z₀ (в), лежат на одной стороне квадрата. Тогда на прямых ВА и АВ лежат стороны квадрата. Дальнейшее продолжение не вызывает трудностей, предлагаем провести самим.

5. Метод подобия (гомотетии).

Сущность метода строят фигуру, подобную данной, не учитывая какой-нибудь линейный размер или специальное положение искомой фигуры относительно данных. Затем строят искомую (чаще всего гомотетией), учитывая, что коэффициент подобия равен отношению любых двух соответственных отрезков.

Задача. Даны угол и точка внутри него. Построить окружность, проходящую через точку А и касающуюся сторон угла.

Анализ. Центр искомой окружности должен лежать на биссектрисе данного угла. Снимем требование, чтобы окружность проходила через А (это подобно тому, что не требуется, чтобы расстояние от точки О до точки окружности равнялось известному отрезку а). Тогда легко построить окружность ₁ , касающуюся сторон утла. Окружности и ₁ гомотетичы (с центром в точке 0). Найдем образы точек А и В: А А, ВВ . Очевидно, АВАВ.

Учитывая оказанное, можно наметить следующий план решения:

1) строим окружность СО₁ , касающуюся сторон угла;

2) проводам ОА;

3) строим точки пересечения и ₁ ;

4) из точки А проводим прямую, параллельную прямой АВ. Пусть В - одна из точек пересечения.

Построение и доказательство опускаем (самим).

Исследование. 1.Окружность ₁ можно построить и бесчисленным множеством способов.

2. Пересечением ОА и ₁ всегда являются две точки А и А.

3. Через точку А можно провести две прямые, параллельные соответственно ВА или ВА. Эти две прямые l₁ и l₂ различны, если А ОВ; и совпадает, если АОВ.

4. Пересечения l₁ ОВ и l₂ ОВ существуют и единственны, если А ОВ , т.е. задача в этом случае имеет два решения.

Если же А ОВ, то этим способом центр искомой окружности не найдем. Для этого принципиально нового случая найдем новое специфичное решение: строим прямую, перпендикулярную ОА-биссектрисе данного угла. Далее проведем биссектрисы углов ОСА и МСА. Точки в₁ и в₂ - искомые центры.

Задача (наглядная). Построить треугольник по двум углам ,

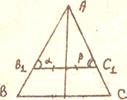
и медиане, проведенной из какой-нибудь вершины.

1. Строим треугольник АВ₁ С₁

2. Подобным преобразованием получим искомый АBC

6. Метод инверсии

Сущность метода: наряду с данными и искомыми фигурами рассматривают фигуры, инверсные им или их частям. Он применяется в тех случаях, когда построение фигуры, инверсной искомой, является более легкой (доступной). Построив инверсную построенной, получают искомую. Метод инверсии дает возможность решить трудные конструктивные задачи. Недостаток - громоздкость (большое число построений).

Задача. Даны: точка О и прямые а и в, не проходящие через О. Построить луч, выходящий из О, чтобы произведение его отрезков от О до точек пересечения с данными прямыми было равно ² , где - длина отрезка .

Анализ. Пусть [ОА) - искомый луч. Тогда ОА*ОВ= ² . Инверсия I относительно окружности (o,r) точку B переведет в точку A, прямую вв, где b - некоторая окружноcть, тогда A = aв.

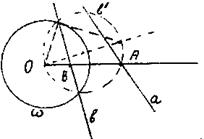
Построение. Строим последовательно: 1) (o,r); 2) в, где в = I (в) окружность, проходящая через О; 3) А, А а в; 4) [ОА) - искомый.

Доказательство. Через В обозначим пересечение в [ОА). Тогда В – прообраз А, т.к. А = [ОА) в[ОА) в = В. По определению инверсии имеем: ОА*ОВ = r² .

Исследование. Если: a в = , то нет решения; - точка касания, то одно решение; a в = {A}, A – точка касания, то одно решение; a в = {A₁ A₂ , A₁ A₂ , то два решения.

Алгебраический метод.

Сущность: решение задачи сводят к построению отрезка, длину которого можно выразить через длины данных отрезков с помощью формул. Затем строят искомый отрезок по полученной формуле.

Задача. Даны: угол АОВ и две точки С и D да луче OВ. Найти на луче [ОА) точку X, чтобы величина угла СХDбыла наибольшей.

Анализ. Пусть точка X найдена. Очевидно, точка X является точкой касания окружности, проходящей через С и D. Обозначим длину отрезка ОХ через х.

Имеем:

х² = |ОС|*|ОD|, |ОС| и |ОD | -

длины известных отрезков ОС и ОD) . План решения состоит из двух шагов: Строим так, чтобы

и х = [OA) (O,x),

где – длина отрезка х.

Построение, доказательство, исследование предлагаем провести самим.

Построение отрезков, заданных формулами.

Алгебраический метод решения задач на построение сводится к построению отрезков, заданных формулами.

Полная формулировка задачи: даны отрезки . Пусть а, в, с,…, d – их длина при некоторой единице измерения. Требуется построить с помощью данных инструментов (циркуля и линейки) отрезок , длина которого x(при той же единице измерения) выражается через длины данных отрезков формулой х = f (a, в² , с,…, d). Будем рассматривать такие значения а, в, с,…,d, при которых f имеет смысл и положительна.

Мы уже знаем, как cтроить выражения

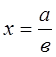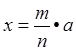, , , , х = а ± в,(а - в, при а

в). К рассмотренным построениям можно свести построение более сложных формул:

1) , n = натуральное число; делается так:

, причем , если n = p·q,

, если n = p² ± q² ;

2)

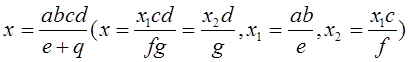
3) · и т.д.

Все построенные выше формулы обладают одним общим cвойcтвом: они являютcя однородными выражениями первой степени. Напоминаем, выражение F(а,…,с) называют однородным степени 11, если

F(ta,…,tc) = tⁿ · F (a,…,c).

Пользуясь понятием однородной функции, мо;но выделить некоторые, классы алгебраичеcких выражений, которые могут быть построены циркулем и линейкой. Например, циркулем и линейкой можно построить:

1) Oтрезок, заданный формулой

,

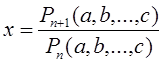где P_{n +1} (…) и P_n (a,b,…,c) - однородные многочлены с рациональными коэффициентами от длин а,в,…,с отрезков степени соответственно n+1 и n.

Пусть

P_{n +1} =

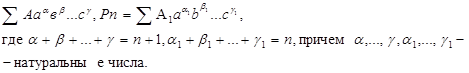
Далее, пусть - произвольный отрезок, d - его длина (в той же единице измерения).

Разделим чиcлитель на dⁿ , знаменатель – на d^{n -1} .

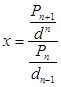
Выражение представляет сумму одночленов вида .

Следовательно, можно построить каждое слагаемое, а потому и весь числитель: 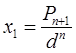. Аналогично, . Наконец строим - отрезок длины х, где ;

2) отрезок, заданный формулой , где – ((…) – однородная рациональная функция 2 степени с рациональными коэффициентами. Делается так: , где (R₂ (…) - отношение двух однородных многочленов , тогда 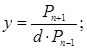как и выше, строим

3) Замечание. При вычерчивании кривых иногда приходится строить алгебраические выражения, не являющиеся однородными первой степени. Пусть надо построить отрезок , длина которого x = f(a,b,…,c), где f(…) не является однородной первой cтепени, например, y = x³ +1.

Правило: построение произвольного выражения от n аргументов всегда можно свести к построению некоторого однородного выражения первой степени от n+1 аргументов. Достигается это выбором единицы измерения.

Выберем некоторый отрезок в качестве единичного, e =1.

-однородная функция первой степени.

Если сумеем построить отрезок по этой формуле, то он и будет искомым при выбранной, единице масштаба. Ясно, что получим различные неравные отрезки в зависимости от выбора .

Примеры:

1)

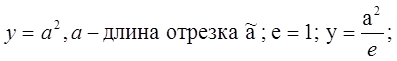
2)

3)

4)

5)

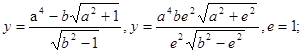
Разрешимость задач на построение с помощью циркуля и линейки.

Для краткости операции «+», «-», «·», «:» и извлечение арифметического квадратного корня» назовем основными действиями.

Теорема. Отрезок, длина которого задается положительной функцией для данных отрезков, может быть построен циркулем и линейкой тогда и только тогда, когда длина искомого отрезка выражается через длины данных отрезков при помощи конечного числа основных действий.

Достаточность. С помощью циркуля и линейки можно построить отрезок , длина которого x равна соответственно:

а+в

а-в

ав (за счет , е = 1)

(- « -)

Так, как по условию длина искомого отрезка выражается через длины данных отрезков с помощью конечного числа основных действий, то остается единственный возможный случай, когда промежуточный отрезок не сможем построить - это построение разности а-в при а в.

В таких случаях перейдем к положительной разности с помощью тождества а - в = - (в - а).

Теперь можно последовательно выполнить все построения, соответствующие основным операциям, и через конечное число шагов получим искомый отрезок.

Необходимость. Ясно, что построение отрезка равносилъно построению его концов. Так как можно построить, то существует конечная последовательность основных построений, в результате выполнения которых на каком-то m -м шаге будет построен один конец (обозначим его через А ), а на к -ом - другой конец (точку в ). На плоскости построим прямоугольную декартовую систему координат.

Пусть А (,), В (, ) - координаты построенных точек. Данные отрезки построим на положительной полуоси ОХ, тогда длины этих отрезков выражаются числами а₁ ,…,а_р (А, В) = х = т.е. длина отрезка выражается через числа , , , с помощью конечного числа основных действий. Если докажем, что сами числа , , , выражаются через а₁ ,…,а_р с помощью конечного числа основных действий, то теорема будет доказана (длина отрезка выражается с помощью конечного числа основных действий).

Заметим, что любые построенные точки в ходе построения появляются двояко: либо выбираемые произвольно, либо как общие точки двух ранее построенных линий.

В первом случае выберем только такие точки, координаты которых выражаются через а₁ ,…,а_р при помощи конечного числа основных действий.

Во втором случае точка получается одним из следующих способов:

а) пересечение прямых (причем каждая прямая проведена через 2 построенные точки):

б) пересечение окружности и прямой (окружность построена через 2 построенные точки);

в) пересечение двух окружностей.

Рассмотрим случай а). Пусть прямая l₁ проведена через точки

C1 (x₁ ,y₁ ) и D₁ (x₂ ,y_2. ). Покажем, что числа х₁ , у₁ , х₂ и у₂ могут быть выражены через а₁ ,…,а_р с помощью конечного числа основных действий (К4ОД). Действительно, пусть уравнение прямой l₁ имеет вид:

в₁ х + с₁ у = d₁

Легко убедиться, что чиcла в₁ ,с_1, d₁ выражаются через х_1, х_2, у_1, у₂ с помощью конечного числа основных действий. То же самое имеет место относительно коэффициентов прямой l₂ : в₂ х + с₂ у + d₂ =0.

Точка пересечения (x₀ , y₀ ) еcть решение cиcтемы

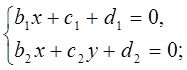
причем решение выражается через в₁ , с₁ ,…, d₁ с помощью КrОД

В cлучае б) (х₀ , у₀ ).- точка пересечения - есть решение системы

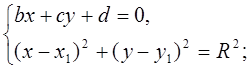
Числа х₀ ,у₀ выражаются через в,с, d, х₁ , х_2, Rc помощью КrОД.

В случае в) точка пересечения (х₀ ,у₀ ) является решением системы

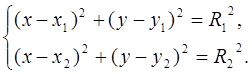
Легко убедиться, что решение выражается с помощью КrОД через координаты ранее построенных точек.

Итак, координаты вновь построенных точек получаются через координаты ранее построенных с помощью конечного числа основных действий. Но, к ранее построенным точкам применимы точно такие же рассуждения. В конечном счете (из-за конечности числа построений циркулем и линейкой) получим, что координаты А и В выражаются через а₁ ,…,а_р с помощью КrОД.

Следствие. Если даны: отрезок, принимаемый за единичный, и число а, то отрезок длины а может быть построен циркулем и линейкой тогда и только тогда, когда число а может быть получено из «I» посредством лишь конечного числа основных действий.

О задачах, не разрешимых циркулем и линейкой.

Большой интерес представляют такие задачи на построения, когда фигура, удовлетворяющая всем условиям задачи, заведомо существует, но не может быть построена указанными инструментами. Такого рода доказательства невозможности даже простых по формулировке задач на построение часто оказываются связанными с наиболее трудными вопросами алгебры, анализа.

Познакомимся с некоторыми классическими задачами на построение, решения которых не могут быть найдены о помощью циркуля и линейки.

1. Задача о квадратуре круга (пользовалась исключительной известностью с древнейших времен).

Построить циркулем и линейкой квадрат, площадь которого бала бы равна площади круга данного радиуса.

Пусть - радиус круга, 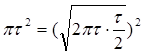, т.е. площадь крута равна площади квадратасо стороной Иначе говоря, x является средней пропорциональной и .

Если бы можно было построить , то легко можно было строить искомый квадрат.

Итак, задача о квадратуре круга свелась к задаче о опрямлении окружности, т.е. построению отрезка длины . При эта длина равна .

Ламберт И. (швейцарский математик) доказал, что - иррациональное число. Но вопрос о возможности спрямления окружности остался открытым, так как согласно следствию из предыдущей теоремы отрезок длины а (при выбранном единичном отрезке) может быть построен циркулем и линейкой, если а получается из I с помощью конечного числа основных действий. Такие числа являются алгебраическими, т.е. служат корнями многочленов с рациональными коэффициентами. Числа, не являющиеся алгебраическими, называются трансцендентными.

В 1882 г. Линдеманн Ф. доказал, что является трансцендентным числом. Следовательно, проблема о квадратуре крута разрешена, задача о квадратуре крута не разрешима о помощью циркуля и линейки.

2. Задачу удвоения куба: зная ребро куба, построить ребро куба, объем которого был бы вдвое больше объема данного.

Пусть а - длина ребра данного куба, x - искомого. Имеем: х₂ = 2а³ . Если а = 1, то получим уравнение х³ – 2 = 0. Это уравнение не имеет рациональных корней (т.к. рациональные корни этого уравнения обязательно целые, их надо искать среди делителей свободного члена). Из алгебры известно: если уравнение рациональные числа) не имеет рационального корня, то ни один корень этого уравнения не может быть выражен через I лишь с помощью конечного числа основных действий. Тогда, учитывая указанное выше следствие, получим, что отрезок длины x не может быть построен с помощью циркуля и линейки.

Замечание. Эта задача может быть решена с привлечением двух прямых углов.

3. Задача о трисекции угла: построить угол, в 3 раза меньший данного.

Достаточно рассмотреть эту задачу для острых углов, т.к. при тупом угол является острым и третья часть равна Отсюда следует, что

Итак, пусть - данный острый угол, - искомый,

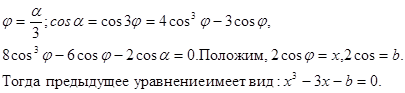
Если отрезок длины x можно построить циркулем и линейкой, то из прямоугольника следует, что можно построить и сам угол . Следовательно, задача свелась к построению отрезка длины х, где x - один из корней уравнения (I).

Пусть = 60, тогда в = 1. Уравнение (I) приводится к виду:

Легко убедиться (из тех же соображений, что и выше), что у этого уравнения нет рациональных корней, следовательно нет ни одного корня, который выражался бы через I с помощью конечного числа основных действий.

Следовательно, задача о трисекции угла не разрешима циркулем и линейкой в общем виде.

Но, может быть, она никогда не разрешима? Это не так. Пусть = 90°. Тогда уравнение (I) имеет вид: x³ - зх = 0, Отрезок можно построить, следовательно, задача в этом случае разрешима.

нетрудно построить и угол .

Можно чисто геометрически построить угол в 60° (хорда равна радиусу, см.рис.).

Замечание 1. Существуют приборы-трисекторы, позволяющие делить угол на три равные части.

АВСD и AB₁ C₁ D₁ - ромбы, =.

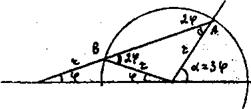
Замечание 2. Задачу о трисекции угла легко решить циркулем. Строим последовательно: 1) окружность расстояние между отметками на линейке;

2) точку А;

3) прямую, проходящую через А так, чтобы расстояние между второй точкой пересечения с окружностью и точкой пересечения этой прямой с прямой ОN было равно .

Построение правильных многоугольников циркулем и линейкой.

Решение проблемы связано большими трудностями, и решена она полностью великим немецким математиком Гауссом в 1796 году.

Вопрос построения правильного n -угольника равносилен вопросу о возможности деления окружности на n равных частей. Возьмем окружноcть радиуcа и прямоугольную систему координат. Задача деления

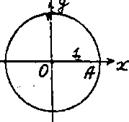
окружности на n равных частей состоит в построении точек

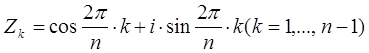
т.е, в построении корней уравнения Zⁿ – 1= 0 о тличных – от Z₀ = 1. Это равносильно построению корней уравнения Это уравнение называется уравнением деления окружности.

Гаусс доказал следующую замечательную теорему.

Теорема. Построение правильного n - угольника с помощью циркуля и линейки возможно тогда и только тогда, когда (числа Ферма).

Рассмотрим несколько частных случаев:

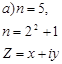уравнение деления окружности. Пусть , (если построено, то также можно построить

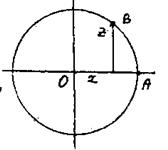
Следовательно, правильный пятиугольник можно построить циркулем и линейкой.

Подставим:

Строим , потом Повторяя дугу АВ 3 раза, получим все точки.

Построения иными инструментами

1. Построения одним циркулем . Во многих случаях построения, проводимые циркулем, оказываются точнее, чем построения, проводимые линейкой.

Итальянский учений Л. Маскерони (1750-1800) и датский ученый Г.Мор (1640-1697) исследовали конструктивные возможности циркуля и доказали следующую теорему.

Теорема (Мора-Маскерони). Любая геометрическая задача на построение фигуры из конечного числа точек, разрешимая циркулем и линейкой может быть решена при наличии только циркуля.

Пояснения: 1) имеется в виду, что фигура состоит из конечного числа точек, окружностей, отрезков, лучей прямых; 2) циркулем конечно, нельзя построить прямую, отрезок, луч, здесь имеется в виду, что циркулем можно сделать их известными (прямая известна, если известны две ее точки; отрезок известен, если известны два его конца; луч известен, если известна начальная точка и точка, через которую проходит луч).

Доказательство опускаем.

2. Построения одной линейкой .

Построения одной линейкой исключительно ограничены. Например, отрезок нельзя разделить пополам. Но если на плоскости задана окружность, возможности увеличиваются.

Справедлива теорема. Всякая геометрическая задача на построение фигуры, состоящей из конечного числа точек, разрешимая циркулем и линейкой, может быть решена одной линейкой, если на плоскости построена окружность и отмечен ее центр (т.е. воли воспользоваться циркулем один раз). Это теорема Штейнера, иногда называют ее теоремой Понселе-Штейнера.

3. Построения двусторонней линейкой

Пример. Разделить данный угол пополам.

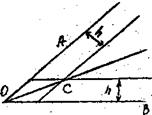
Проводим параллели, ОС - биссектриса

Оказывается, справедлива теорема

Всякая геометрическая фигура, состоящая из конечного числа точек, которая может быть построена циркулем и линейкой, может быть построена только двусторонней линейкой.

4. Построения с помощью прямого угла.

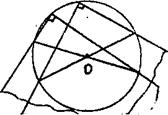
Пример. Построить центр начерченной окружности. Всякая геометрическая фигура, состоящая из конечного числа точек, которая может быть построена циркулем и линейкой, может быть построена только прямым углом. Это же верно для любого угла.

Пример 2. Дан АВС; требуется построить три окружности так, чтобы каждая из них касалась двух других окружностей и двух сторон треугольника (задача Мальфатти). Считаем задачу решенной (фиг. 1). Пусть точка О будет центром вписанной в треугольник окружности (радиуса r). Радиусы кругов К и L обозначим соответственно через r₁ и r₂ . Из точек К, О, L опустим перпендикуляры на сторону АВ и таким путем построим точки D, Е, F. Положим AE = s, BE = t, AD = x, BF = y.

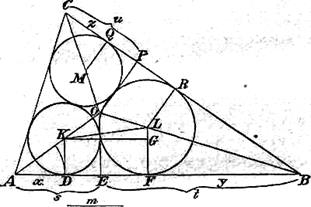
Фиг. 2

Если мы проведем KG || AB, то

LG = r₂ – r₁ и KG =

Из подобия 7) треугольников ADK и AEO следует, что

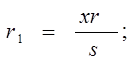
аналогично этому и 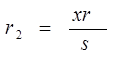, что вытекает из подобия треугольников BFL и ВЕО.

AB = AD + DF + FB,

следовательно:

=

или (подставляя вместо r₁ и r₂ полученные для них выражения)

= (1)

Если опустим из точек L, М,О перпендикуляры на сторону ВС и положим РС = и и QC = z, то получится равенство

2) = t + u;

аналогично мы получим равенство и для третьей стороны :

3) 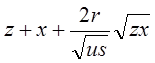= u + s.

Таким образом, мы имеем три уравнения для определения трех неизвестных х, у, z.

Мальфатти сообщает решения этих трех уравнений,:

Если подставить эти значения в вышеприведенные уравнения, то они удовлетворят последним. Путь, которым Мальфатти нашел решения, чрезвычайно сложен, как он сам указывает.

Геометрическое же построение величин х, у, z представляется чрезвычайно простым, ибо

вследствие чего отрезки эти, равно как и отрезки s, t, r, u, r, легко могут быть построены.

Если же теперь построить выражение

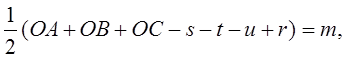
x = ОА — m, у = ОБ — m,

z = OC - m (фиг. 2).

Пример 3. Даны три окружности K₁ , K₂ , К₃ , коих центры лежат на одной прямой; радиус каждой из окружностей К₁ , К₂ равен r₂ . Последние две окружности имеют одно и то же центральное расстояние а от окружности К₁ {r₁ ). Требуется построить все окружности, которые касаются трех данных (фиг. 3).

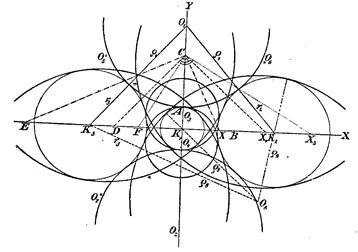
Фиг.3.

Для того, чтобы решить эту задачу вычислением, мы кладем в основание прямоугольную систему координат. При этом уравнения данных окружностей таковы:

К₁ … х² +у² = ,

K₂ … (x - a)² + y² =

K₃ … (x + a)² + y² =

Уравнение же каждой из искомых окружностей имеет вид:

(x - p_i )² + (y - q_i )² = _i ² .

Для круга О₁ (фиг. 3) легко могут быть получены три уравнения, определяющие три неизвестные велиeчины p₁ , q₁ , ₁ ; именно, из условий

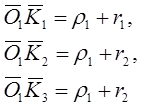
вытекают равенства

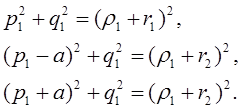
Из двух последних следует, что p₁ = 0, а отсюда уже непосредственно вытекает:

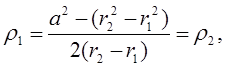(1)

ибо радиус круга О₂ равен радиусу ₁ круга О₁ (фиг. 3).

Окружность О₃ касается окружностей К₂ и К₃ извне, а окружности К₁ — изнутри; таким образом, имеют место равенства

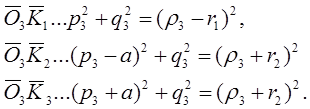
Отсюда получается

(2)

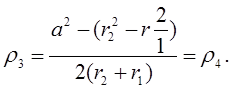
Для окружности О₅ имеют место равенства

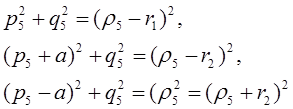
откуда получается:

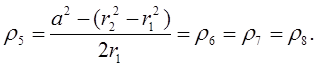
Построение может быть выполнено по следующему плану. Строим по порядку (фиг. 3):

AB = r2, BC = a,

тогда

если затем построить

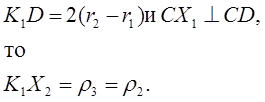
Аналогично построим

1. Весьма удобным методом для решения геометрических задач на построение является метод геометрических мест.

Он основывается на следующем: стараются свести всю задачу к нахождению некоторой точки X, что в большей части случаев сделать не трудно.

Точка X определяется двумя условиями, вытекающими из требования задачи. Если устранить первое из условий, то существует не одна только точка X, но бесчисленное множество таких точек, составляющих в совокупности некоторую линию, некоторое геометрическое место. Если же устранить второе условие и ограничиться первым, то получится другое геометрическое место. Каждая точка пересечения этих двух геометрических мест удовлетворяет требованиям задачи.

2. Является необходимым предварительно изучить некоторые геометрические места. Мы приведем наиболее простые и вместе с тем наиболее употребительные из них.

a) Геометрическое место точек, находящихся от данной точки на данном расстоянии, есть окружность, описанная из данной точки, как из центра, радиусом, равным данному расстоянию.

b) Геометрическое место точек, находящихся на данном расстоянии от данной прямой, состоит из двух прямых, проведенных параллельно данной прямой, на данном от нее расстоянии.

c) Геометрическое место точек, равноотстоящих от двух данных точек А и В, есть прямая, перпендикулярная к отрезку АВ в его середине. (Симметраль точек А и В).

d) Геометрическое место точек, равноотстоящих от двух данных прямых, состоит из двух взаимно перпендикулярных прямых делящих пополам углы между данными прямыми (биссектрисы).

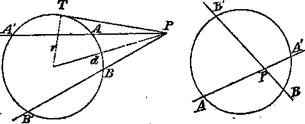
e) Геометрическим местом точек, из которых отрезок АВ виден под данным углом а, является дуга окружности, стягиваемая* отрезком АВ (построение ясно из фиг. 4).

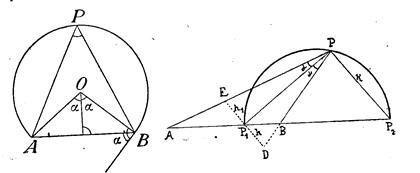
Фиг. 4 Фиг. 5

f) Геометрическое место точек, расстояния которых от двух данных точек находятся в данном отношении m : n, есть некоторая, окружность (фиг. 5)

При этом

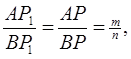
Откуда по известной теореме получается , что APP₁ = P₁ PB.

Имеет место также пропорция

AP₁ :P₁ B = AP₂ :BP₂

Четыре такие точки называются, как известно, четырьмя гармоническими точками.

g) Геометрическое место точек, расстояния которых от двух данных прямых находятся в данном отношении m : n, образуется двумя прямыми линиями х и у, проходящими через точку пересечения данных прямых (фиг. б).

h) Геометрическое место точек, квадраты расстояний которых от двух данных точек А и В сохраняют постоянную разность d² , есть прямая, перпендикулярная к отрезку АВ.

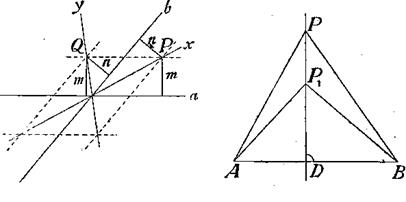
Фиг. 6 Фиг.7

Доказательство: Пусть точка Р₁ (фиг. 7) обладает указанным свойством, так что

Если опустить из точки P₁ на АВ перпендикуляр и взять на нем произвольную точку Р₁ то

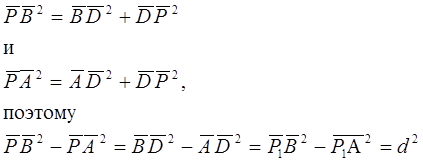
Из h) может быть выведено следствие, которое позже для нас будет важно. Мы лишь предпошлем ему краткое замечание:

а) Как известно, справедливо следующее предложение: „Если через точку Р (фиг. 8а, 8_Ь ) провести секущие к окружности, то постоянно

РА .РА = РВ.РВ = ...

Эго постоянное произведение называется степенью точки Р в отношении данной окружности; степень равна d² — r² , где d есть расстояние точки Р от центра (центральное расстояние точки Р), r есть радиус окружности.

Фиг. 8а Фиг. 8б

Если точка Р лежит вне окружности, то степень точки также равна РТ² .

) Если даны две окружности с центрами О₁ и О₂ , то точка Р имеет определенную степень по отношению к каждой из них. Если же точка Р по отношению к обеим окружностям (с радиусами r₁ и r₂ ) имеет одну и ту же степень, то

так что

следовательно, геометрическое место точек, имеющих одну и ту же степень в отношении обеих окружностей, есть (согласно h) прямая, перпендикулярная к линии центров этих окружностей; прямая мл называется радикальной осью обеих окружностей.

Если окружности пересекаются, то их радикальная ось проходит через точки их пересечения, ибо каждая из точек пересечения имеет в отношении обеих окружностей степень, равную нулю.

Если же окружности не пересекаются, то радикальную ось можно построить (фиг. 9), опустив перпендикуляр на линию центров из середины общей касательной к обеим окружностям; можно при этом следовать и другому пути, пользуясь теоремой: „Если даны на плоскости три окружности, то определяемые ими три радикальные оси проходят через одну и ту же точку (радикальный центр трех окружностей); доказательство теоремы основывается на том соображении, что точка пересечения двух каких-либо радикальных осей имеет одну и ту же степень в отношении всех трех окружностей, следовательно, лежит на третьей радикальной оси.

Фиг. 9

3. Мы разъясним метод геометрических мест на двух примерах:

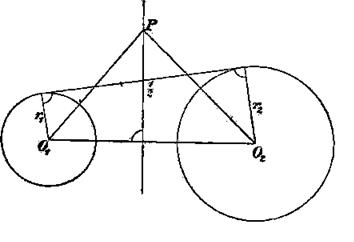
а) Даны две окружности О₁ , О₂ радиусов r₁ и r₂ .

Требуется построить такую окружность К₁ которая касалась бы обеих данных окружностей и имела бы данный радиус r.

Если откинуть требование, чтобы окружность К касалась окружности О₂ , то искомых окружностей существует бесчисленное множество; геометрическое место их центров состоит из двух концентрических с О₁ окружностей, радиусы которых соответственно равны r₁ + r и r₁ — r. Аналогично мы получим для искомого центра X и другое геометрическое место, состоящее из двух окружностей, описанных из точки О₂ , как из центра, радиусами

Точка X должна совпасть с одной из точек пересечения обоих геометрических мест; существует не больше восьми точек, удовлетворяющих требованиям задачи.

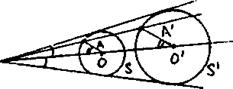
) Даны три окружности K₁ , К₂ , К₃ ; требуется построить все окружности, касающиеся трех данных (Аполлониева задача о касании).

Если (фиг. 10) через центр одной из данных трех окружностей, например, через центр окружности /С3, провести окружность, концентрическую с искомой X, то окажется, что упомянутая выше задача сведется к следующей:

Даны две окружности К₁ , К₂ и точка Р; требуется построить окружности, касающиеся двух данных и проходящие через точку Р.

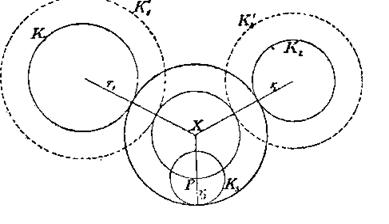
Фиг. 10

Геометрическое место центров всех окружностей, которые касаются окружности К₁ и проходят через точку Р, есть эллипс или гипербола, в зависимости от того, лежит ли Р внутри окружности К₁ или вне ее.

Центр окружности К₁ и точка Р являются фокусами этих конических сечений; асимптоты гиперболы перпендикулярны к касательным, которые можно провести к окружности К₁ из точки Р.

Каждая из данных трех окружностей может свестись и к одной точке или перейти в прямую. Геометрическое место центров окружностей, которые касаются прямой l и проходят через точку Р, есть парабола, имеющая прямую l своей директрисой, а фокус — в точке Р.

Вариант 15

1. Построить треугольник АВС по а, с-b,

2. Построить трапецию по отношению боковых сторон, углу между ними и двум основаниям.

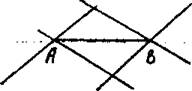
3. Даны прямая МNи точки A и В в одной полуплоскости относительно прямой MN. Поcтроить на прямой МN точку X такую, что

.

4. Вписать в данный четырехугольник параллелограмм так, чтобы его центр совпал c данной точкой.

5. В данном круге через данную внутри его точку А провести хорду так, чтобы она в точке А разделилась в отношении m : n.

6. Построить треугольник с данным отношением сторон длин биссектрисы и медианы, проведенных из одной вершины.

7. Построить прямоугольной треугольник по радиусам описанной окружности R и вписанной окружности r.

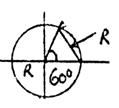
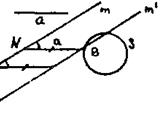
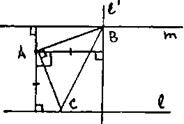
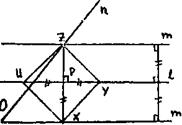
8. На приведeнных ниже чертежах дано схематичное решение четырех задач на, построение. Сформулировать эти задачи и дать их полное решение.

1)	2)
3)	4)

9. Построить ромб, зная его сторону а и отношение диагоналей р : q, где pи q заданные отрeзки. Решить задачу двумя способами.

10. Рассматриваются всевозможные треугольники c данными основанием a, угол при вершине которых равен . Найти множество точек пересечения медиан

Скачать архив с текстом документа