Графический метод изучения механического движения

СОДЕРЖАНИЕ: Первый параграф: Механическое движение, его виды характеристики и виды

ГОУ Гимназия №1505

«Московская городская педагогическая гимназия-лаборатория»

Реферат

Графический метод изучения механического движения.

автор : ученика 10 класса «Б»

Стариченкова Александра

Руководитель: Пурышева Н.С.

Москва

2011

ОГЛАВЛЕНИЕ:

ВВЕДЕНИЕ ……………………………………………………………………2-3

ТЕОРЕТИЧЕСКАЯ ЧАТЬ …………………………………………………. 4-11

Первый параграф: Механическое движение, его виды характеристики и виды………………………………………………………………………… 4-5

Второй параграф: Виды графиков функциональной зависимости… 6-9

Третий параграф: Решение кинематических задач………………… 10-11

ПРАКТИЧЕСКАЯ ЧАСТЬ ………………………………………………... 12-20

Параграф первый: конспект урока…………………………………….. 12-14

Параграф второй: система кинематических задач………………… 14-20

ЗАКЛЮЧЕНИЕ …………………………………………………………........ 21

СПИСОК ЛИТЕРАТУРЫ …………………………………………………… 22

ВВЕДЕНИЕ.

Физика и математика, как науки, очень тесно связаны между собой. Можно сказать, что это даже родственные науки. Если происходят открытия в сферах одной из этих наук, то и непременно начинают развиваться схожие сферы в другой. В конце XVII века, например, было открыто дифференциальное и интегральное исчисление И. Ньютоном, Г. Лейбницем и сформулированы основные законы классической механики и закон всемирного тяготения тем же И. Ньютоном. Из этой последовательности видно, что открытие в математике (дифференциальное и интегральное исчисление) дало ход новым открытиям и в физике (классической механики и закон всемирного тяготения). Уловить и почувствовать эту связь удаётся не каждому. Жаль, что часто во многих школах очень слабо дают понять ученикам эту самую связь. И я решил, что с помощью использования графического метода решения механических задач я смогу уловить связь между этими науками.

Выявит и реализовать связь физики и математики в решении механических задач – это основная цель моего диплома. Для реализации этой цели я поставил перед собой следующие задачи:

1) Изучить литературу по теме;

2) Рассмотреть графики функциональной зависимости всех видов;

3) Рассмотреть виды механического движения и графики зависимости движения от времени;

4) Разработать систему графических задач по теме, с использованием математического представления.

Метод решения, поставленных передо мной задач, один: анализ и обобщение литературы.

Результатов, которых я хочу добиться, два: во-первых, выявит и реализовать связь физики и математики, а во-вторых, разработать систему задач, с примерами их решения.

Мой диплом состоит из двух частей: теоретической и практической. В теоретической части я подробно опишу всё что связано с механическим движением и все виды графиков функциональной зависимости. В практической части будет представлен подробный план урока, который я собираюсь провести у 9-ых классов профиля физика, а также система задач по кинематике, которые решаются графическим методом, т.е. с использованием математического аппарата.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ.

МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ ТЕЛ, ЕЁ ХАРАКТЕРИСТИКИ И ВИДЫ МЕХАНИЧЕСКОГО ДВИЖЕНИЕ. ВИДЫ ГРАФИКОВ ФУНКЦИОНАЛЬНОЙ ЗАВИСИМОСТИ. РЕШЕНИЕ КИНЕМАТИЧЕСКИХ ЗАДАЧ.

Первый параграф: Механическое движение, его виды характеристики и виды.

Механическое движение – изменение положения тела в пространстве относительно других тел с течением времени. В физике за тело, которое совершает такое движение, принято принимать материальную точку [1] . Положение такого тела во время совершения механического движения задаётся с помощью системы отсчёта , которую составляют тело отсчёта , система координат и способ измерения времени (часы). Последовательность точек, которые проходит тело во времени движения, называют траекторией движения тела в пространстве . Расстояние, пройденное телом вдоль траектории за рассматриваемый промежуток времени t, называют путём S , который является величиной скалярной[2] . Вектором перемещения принято называть вектор, соединяющий начальное и конечное положение тела. Чтобы получить значение модуля вектора перемещения, нужно вычислить корень квадратный из суммы квадратов проекций (скалярные величины) перемещения на оси системы координат. Все эти понятия можно объединить в группу, которая называется кинематическими[3] характеристиками движения материальной точки .

В зависимости от формы траектории тела есть два вида механического движения: прямолинейное и криволинейное , которое в свою очередь может быть произвольным , например траектория представляет собой зигзаг, или движение по окружности . В зависимости от изменения скорости тела механическое движение также можно разделить на два вида: равномерное , т.е. за любые равные промежутки времени тело совершает одинаковое перемещение, и неравномерное . Неравномерное бывает двух видов: неравномерное произвольное , т.е. за равные промежутки времени тело совершает абсолютно разные перемещения, и неравномерное равноускоренное , т.е. за любые равные промежутки времени скорость тела изменяется на одинаковые величины, т.е. это имеет постоянное ускорение . Ускорение есть векторная физическая величина, равная отношению изменения скорости ко времени, за которое это изменение произошло (V/t). Скоростью , или точнее мгновенной скоростью , называют векторную величину, равную отношению малого перемещения к малому промежутку времени, за который это перемещение произошло (r/t).

Поскольку и перемещение, и скорость, и ускорение есть векторные величины, то можно сказать о том, что их можно задать тремя проекциями на оси координат.

Для представления движения часто удобно пользоваться графиками, так как они дают наглядное представление о характере изменения величин с течением времени. В кинематике используются графики зависимости скорости движения от времени; график зависимости модуля перемещения от времени; графики зависимости координаты тела от времени, графики зависимости пути, пройденного телом при движении, от времени.

Второй параграф: Виды графиков функциональной зависимости.

Как известно, анализируя график движения, можно получить исчерпывающие сведения о характере движения. Так, из анализа графиков скорости, показанных на рисунке:

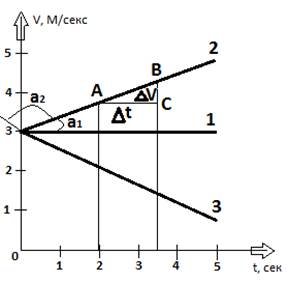
можно сказать, что движение 1 есть равномерное прямолинейное движение со скоростью 2 м/сек в сторону положительного направления оси координат. Движения 2 и 3 – равноускоренное прямолинейные движения (линейная зависимость y = a + bx ) с начальной скоростью 2 м/сек положительного направления оси выбранной системы отсчёта (V0 в течение всего времени движения). Более того, если выбрать любой промежуток времени t и определить изменение скорости за этот промежуток, то отношение V/t определит величину ускорения, с которым двигалось тело. Из ABC видно, что отношение V/t равно тангенсу угла наклона графика к оси абсцисс.

Следует заметить, что если угол находиться в первом и третьем квадранте[4] координатной плоскости, то tg 0, ускорение a0; если угол находиться во втором или четвёртом квадранте, то tg 0, ускорение a0. Аналагично и с графиком равномерного движения: если tg 0 скорость V0; tg 0, скорость V0.[5] Кроме того, если говорить о равноускоренном движении, то стоит продемонстрировать какие ещё графики функциональной зависимости можно изобразить используя ускорение (a), скорость (V), координату (x), перемещение (S). Во-первых график проекции скорости от времени:

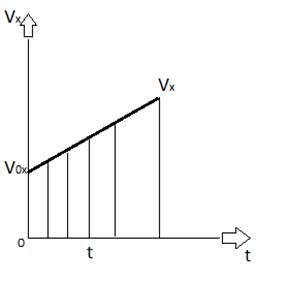
используя этот график можно вывести формулу для изменение координаты тела с течением времени, совершающее одинаковое перемещение (x = x 0+ V 0 x +( axt /2) ).

А уже из этой формулы можно вывести зависимость между разностью квадратов проекций начальной и конечной скоростей тела и произведения проекции ускорения и перемещения ( Vx - V 0 x =2 axSx ) .

Так же необходимо понять, используя полученные нами формулы, что проекция ускорения на графике функции будет параллельна оси координат, на которой откладывается значение времени, т.к. ускорение во время движения тела остаётся неизменной величиной. А со скоростью как раз наоборот – поскольку это величина изменяемая в данном случае, её проекция будет находиться под углом в оси времени (чем больше изменение скорости, тем больше угол):

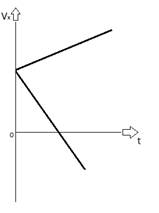
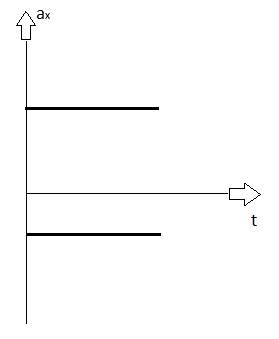
график зависимости проекции график зависимости проекции скорости от времени ускорения от времени

Как видно из графиков и ускорение, и скорость в равноускоренном движении могут быть меньше нуля, но если ускорение меньше нуля, то это значит, что тело движется в противоположную сторону от направления оси, а если скорость меньше нуля, то, во-первых, тело замедлялось, а затем начала увеличивать свою скорость в противоположную сторону от направления оси.

Рассматривая график зависимости координаты тела от времени в равноускоренном движении, следует учитывать тот факт, что в отличии скорости и ускорения, координата тела не может быть меньше нуля. Кроме того в зависимости от того какое ускорение, положительное или отрицательное, будет строиться график:

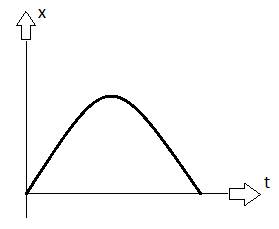
ускорение положительное ускорение отрицательное

Почему второй график значительно отличается от первого? Чтобы ответить на этот вопрос представим ситуацию: мы с силой толкаем шарик по желобу вверх. В этот момент он имеет положительное ускорение и двигается по направлению выбранной нами оси координат. Через какой-то малый промежуток времени он полностью теряет свою скорость, достигнув пика своего движения, т.е. его координата максимальна. И, естественно, он начинает двигаться назад, приобретая при этом отрицательное ускорение, отрицательную скорость, но координата по прежнему у него положительная. Проще говоря он стремится вернуться в обратное состояние, в начальную точку, где мы его толкнули. А эта начальная точка есть минимум его движения, т.е. ноль. Вот как и получается второй график.

Ну а объяснить, как строиться первый график ещё проще: просто возьмите шарик с гелием и отпустите его. Он улетит бесконечно вверх, ну пока не лопнет, имея положительное ускорение, положительную скорость и бесконечно увеличивающуюся координату.

Третий параграф: Решение кинематических задач.

Основная задача кинематики состоит в том, чтобы вычислить местоположение тела в любой наперёд заданный момент времени, если известны его начальные координаты, а также скорость и ускорение.

Так как механическое движение относительно, т.е. любое утверждение о нём зависит от системы отсчёта, то решение кинематических задач начинается с выбора системы отсчёта. Выбрать систему отсчёта – это значит выполнить следующий ряд действий:

1. Указать тело (или систему тел) отсчёта и связать с ним начало координат.

2. Выбрать положительное направление осей координат.

3. Указать момент начала отсчёта времени.

4. Выбрать масштаб измерения времени (час, минута, секунда).

Выбор системы отсчёта определяет начальное условия, т.е. указывает, где

находиться тело (материальная точка) в тот момент времени, который принят за начало отсчёта времени. Это первоначальное положение тела может быть охарактеризовано либо тремя координатами xo,yo,zo, либо радиус-вектором , проведённым из начала координат в точку с координатами xo,yo,zo.

При движении тела координаты его изменяются. Координаты тела в любой наперёд заданный момент времени t вполне определяются радиус-вектором. Как известно, перемещение , или .

Итак, чтобы знать местоположение тела в любой момент времени t, надо знать (или, что то же, xo,yo,zo – начальные координаты) и — перемещение, которое совершает тело за рассматриваемый промежуток времени t-to.

Для некоторых простых случаев движения перемещение может быть легко вычислено. Так, для равномерного прямолинейного движения ,а для равнопеременного прямолинейного движения . Каждому из этих векторных уравнений соответствует три скалярных уравнения:

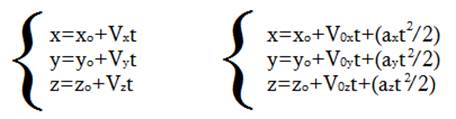
Однако в случае прямолинейного движения ось OX можно выбрать всегда так, чтобы она совпадала с траекторией. В этом случае y=yo=04; z=zo=0, и для каждого их этих движений имеется лишь одно уравнение x=xo+Vxt и x=xo+V0x+(axt/2).

Величина проекции скорости равна модулю вектора скорости Vx=, величина проекции ускорения равна модулю вектора ускорения ax= , а знак проекций зависит от выбора положительного направления оси OX.[6]

ПРАКТИЧЕСКАЯ ЧАСТЬ.

КОНСПЕКТ УРОКА. СИСТЕМА ЗАДАЧ ПО КИНЕМАТИКЕ.

В данной части моего диплома представлен конспект урока в 9 классе физико-математического профиля на тему «Решение графических задач по кинематике». Отдельно приведена система задач, которые следует решить на данном уроке.

Параграф первый: конспект урока.

В первом параграфе описан план проводимого мною урока, цели, которые поставлены передо мной при проведении этого урока и средства их исполнения.

ЦЕЛИ УРОКА И СРЕДСТВА ИХ РЕАЛИЗАЦИИ.

Я поставил перед уроком три образовательные цели:

Цель обучения - развить умение учащихся применять графический метод решения кинематических задач, т.е. помочь учащимся правильно выбирать задачи, которые легче решить, используя именно графический метод.

Цель развития - развитие логического мышления учащихся при работе с графиками разных функциональных зависимостей. Для реализации этой цели следует сначала подробно разобрать этапы применения графического метода решения кинематических задач, а затем, решая с учениками задачи, научить их порядку действий при работе с графиками.

Цель воспитания - развитие графической культуры учащихся профильной физико-математической группы при решении задач по кинематике. Приобретая графическую культуру, учащиеся овладевают универсальным учебным умением работать с графической информацией. Универсальным его называют потому, что, овладев им, учащиеся способны применить данное умение не только при решении физических задач, но при работе с графиками на межпредметном (МП) и метапредметном (внепредметном) уровнях.

Основой достижения каждой из поставленных целей являются установление и реализация межпредметных связей (МПС) физики и математики, которые установлены в данной работе.

Средствами обучения являются разработанные мной дидактические материалы и электронные обучающие ресурсы (ЭОР), т.е. компьютерные программы, предусматривающие построение графиков.

ПЛАН УРОКА.

Весь урок я разбил на четыре этапа:

Организационный момент. За две минуты после звонка на урок вполне реально успокоить учеников и настроить их на работу.

Актуализация знаний. После того как ученики будут готовы к работе, необходимо, задавая вопросы по пройденному ранее материалу курса физики, повторить изученный материал, актуализировать имеющиеся знания и подготовить таким образом учащихся к восприятию нового материала. При этом необходимо актуализировать и знания о графиках функций, полученных учащимися при изучении математики. Приблизительно этот этап урока должен занять около 7 минут.

Вопросы для актуализации знаний:

1) Какие виды механического движения существуют?

2) Как записывается уравнение зависимости пути, проекции перемещения и координаты от времени для равномерного движения?

3) Как записывается уравнение зависимости скорости, проекции скорости, пути, проекции перемещения и координаты от времени для равноускоренного движения?

4) Как записывается уравнение линейной функции?

5) Какой вид имеет график линейной функции?

6) Задачи № 3, 10, 11 (Рымкевич). Использование этих задач, которые представляют собой обычные вопросы с вариантами ответов, позволит быстро и легко восстановить пройденный материал.

Решение задач. Сначала на примере одной задачи разбирается графический метод решения кинематических задач, а затем оставшееся время ученики самостоятельно решают похожие задачи. Моя роль - помочь им, если возникнут трудности. Все задачи, которые решаются на уроке, приведены во второй главе практической части. Решение задач займёт большую часть урока, т.е. приблизительно 34 минуты.

Обобщение знаний и подведение итогов урока. На этом этапе урока делаются выводы, обобщается пройденный на уроке материал. Этот этап занимает последние две минут до звонка на перемену.

Выводы по уроку и анализ проведенного урока описаны в заключение моего диплома.

Второй параграф: система кинематических задач.

В данном параграфе представлена система задач, которые я собираюсь использовать во время своего урока у 9-ых классов, а точнее во время конкретно части урока, которую я назвал непосредственно «решение задач».

Для начала необходимо разобраться, как же всё-таки с помощью графического метода, т.е. используя математический аппарат, решать кинематические задачи по физике. Сейчас я полностью разберу этот метод на одной из задач по кинематике.

Текст задачи: Пусть дан график скорости. Какое движение описывает этот график?

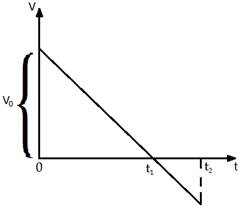
График скорости показывает, что в начальный момент времени тело имело некоторую скорость и двигалось вдоль положительного направления ос OX (0 ). Скорость его по модулю равномерно уменьшалась, тело двигалось равнозамедленно (V 0, a 0 ). В момент времени оно на мгновение остановилось (V =0 ), а затем стало двигаться в обратном направлении (V 0 ) с прежним ускорением (a 0 ), но теперь его движение будет равноускоренным (знаки проекций векторов скорости и ускорения одинаковые). Сделаем чертёж движения. Пусть тело начало двигаться из точки, находящейся в начале координат, и за время (=0 ) прошло равнозамедленно путь до точки А, а затем за время , двигаясь равноускоренно, прошло путь в обратном направлении от точки А до точки В.

Всё, что было описано до графика, изображающего путь пройденным телом, является одним из пунктов решения кинематических задач графическим методом, который называется «анализ задачи». В данном пункте решающий должен чётко понимать как и куда двигалось тело, смотря на лежащий перед график скорости, как например в этой задачи. Дальнейшие рассуждения приведут к ответу и финальному изображению графика перемещения:

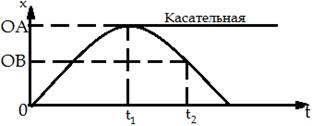
На полученном графике, который приведён выше, по оси ОХ откладывается само перемещение, а по оси ОY – время, за которое это перемещение было совершенно телом.

Так же в некоторых задачах просят построить графики пути, перемещения, ускорения, скорости используя данный вам по задачи график. Например, опять же дан график изменения скорости (граф. 1), следовательно, ученикам необходимо изобразить графики пути и перемещения. Проведя «анализ», а затем непосредственно «решение», используя известные им физические и математические формулы, они приступают к финальному пункту таких задач – «построение». Основным требованием к данному пункту является строгое соблюдение направлений модулей векторов, исходя из выводов, сделанных во время «анализа». Исходя из данных графика №1, после завершения всех пунктов решения, у учеников должны получиться графики №2, на котором изображён путь, и график №3, на котором изображено перемещение:

График №1 :

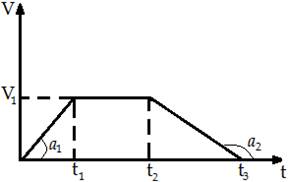
График №2 :

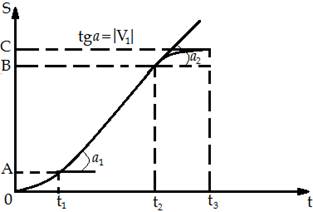
График №3 :

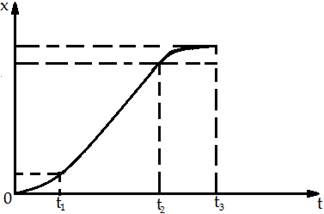
Итак, я полностью разобрал каждый пункт решения кинематических задач, используя математический аппарат, т.е. графический метод, и теперь переду непосредственно к самой системе подготовленных мною к уроку задач. Задача №1:

По заданному графику найти начальные координаты тел и проекции скорости их движения. Написать уравнение движения тел x = x(t). Из графиков и уравнений найти время и место встречи тел, движения которых описываются графиками 2 и 3.

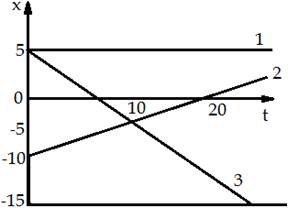
Задача №2:

Начертить графики ускорения, пути и перемещения по данному графику скорости.

Задача №3:

Дан график зависимости скорости тела от времени. Построить график пути, перемещения и ускорения тела.

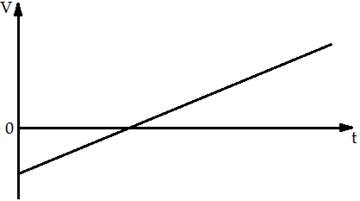
Задача №4:

Спортсмен бежит равномерно по кругу радиусом R со скоростью V. Постройте график пути и перемещения спортсмена, приняв точку старта за начало отсчёта.

Задача №5:

Построить графики скорости, ускорения, пути и перемещения тела, брошенного вертикально вверх и упавшего обратно.

Задача №6:

Графики движения двух тел представлены на рисунке. Что означают точки пересечения графиков с осями координат.

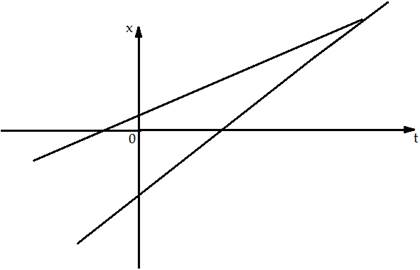
Задача №7:

График зависимости ускорения тела от времени представлен на рисунке. Начертить графики зависимости скорости, координаты и пути, пройденного телом, от времени. Начальная скорость тела равна нулю (на участке разрыва ускорение равно нулю).

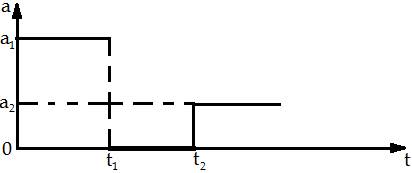
Задача №8:

На рисунке представлен график зависиимости координаты тела от времени, После момента времени кривая графика – парабола. Указать характер движения тела.

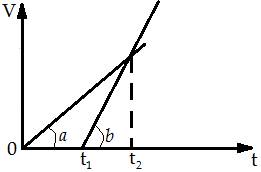
Задача №9:

На рисунке представлены графики скоростей для двух тел, движущихся по одной прямой из одной и той же начальной точки. Известны моменты времени и . В какой момент времени тела встретятся?

ЗАКЛЮЧЕНИЕ.

За время работы над своим дипломом, а точнее проводя исследовательскую работу, я выяснил в чём проявляется межпредметная связь между такими «родственными» науками как математика и физика. Весь материал, который был мною использован, т.е. книги из списка литературы, был очень полезен и лёгок к восприятию. Теоретическая часть была ни только поучительной, но и дала мне шанс вспомнить материал прошлых лет, что несомненно помогло мне в самой исследовательской работе.

К сожалению, мне не удалось провести урока у 9-ых классов на профиле физика. Но практическую я часть я всё равно выполнил. Подготовка с руководителем и подборка задач дали мне шанс освоить первые навыки преподавания, а значит подготовили меня к первому моему шагу к достижению основной цели, поставленной передо мной во время начинания работы над данной темой.

Итак, из всего выше сказанного можно сделать вывод, что за весь этот период работы над дипломом, я выучил несколько вещей: во-первых, как правильно выбирать и обобщать нужную мне литературу, во-вторых, понимание происхождения межпредметной связи между математикой и физикой, и в-третьих, начальные навыки преподавания физики.

Несомненно, за будущий год я ещё успею набрать больше опыта в этих навыках и постараюсь опробовать себя в роли учителя, используя план урока, который представлен в первом параграфе практической части диплома.

СПИСОК ЛИТЕРАТУРЫ.

1) С. В. Анофрикова, Э. Г. Ахтырченко, Л. А. Иванова, С. Е. Каменецкий, Т. И. Носова, Н. Е. Парфентьева, Н. С. Пурышева «Механика. Факультативный курс. Пособие М 55 для учителей» - М., Просвещение, 1971.

2) Э.К.Немченко «Новейший полный справочник школьника: 5-11 классы. В 2т. Т.I» - М.: Эксмо, 2009.

[1] Материальная точка (простейшая физическая модель в механике – математическая абстракция) – тело, размерами которого мы можем пренебречь в условиях данной задачи.

[2] Скалярная величина (от лат. Scalaris – ступенчатый) в физике – величина, каждое значение которой может быть выражено одним действительным числом. То есть скалярная величина определяется только своим значением, в отличие от вектора, который кроме значения имеет направление.

[3] Кинематика (греч. – двигаться) – раздел механики, в котором рассматриваются различные виды движения с геометрической точки зрения, т.е. изучается, каковы координаты материальной точки в любой момент времени. Причины движения здесь не рассматриваются.

[4] Квадрант – четверть круга.

[5] С. В. Анофрикова, Э. Г. Ахтырченко, Л. А. Иванова, С. Е. Каменецкий, Т. И. Носова, Н. Е. Парфентьева, Н. С. Пурышева «Механика. Факультативный курс. Пособие М 55 для учителей» - М., Просвещение, 1971.

[6] С. В. Анофрикова, Э. Г. Ахтырченко, Л. А. Иванова, С. Е. Каменецкий, Т. И. Носова, Н. Е. Парфентьева, Н. С. Пурышева «Механика. Факультативный курс. Пособие М 55 для учителей» - М., Просвещение, 1971.

Скачать архив с текстом документа