Имитационная модель системы автоматизированного проектирования абстрактного этапа реализации устройств управления
СОДЕРЖАНИЕ: Для дискретных систем управления интерпретируемых конечными автоматами предложена система их проектирования в виде параллельно функционирующих стандартных компонентных автоматов.на стандартных составляющих
Дзугкоева А.А.
Кафедра информационных систем в экономике.
Северо-Кавказский горно-металлургический институт (государственный технологический университет)
Для дискретных систем управления интерпретируемых конечными автоматами предложена система их проектирования в виде параллельно функционирующих стандартных компонентных автоматов. Приведена имитационная модель системы, описано её функционирование.
Для реализации системы логического управления (управляющего автомата) совокупностью параллельно функционирующих автоматов из некоторого стандартного набора была создана подсистема автоматизированного проектирования абстрактного этапа.
Для оценки эффективности разработанной подсистемы, анализа её характеристик, правильного сопряжения отдельных блоков друг с другом была разработана имитационная модель представленная на рисунке.
В процессе моделирования с генератора случайных графов на вход системы поступает граф 
, так же случайным образом из стандартного набора автоматов поступает графоид автомата 
. Кроме того, задаётся ограничение 
на мощность множества состояний в искомом компонентном состоянии.
Для получения автомата 
, такого, что 
, 
необходимо отождествить состояния А с парами состояний – первое из В, второе из С. Задача эта решается последовательно в два этапа.
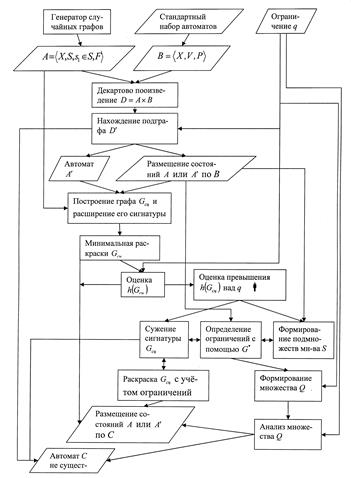
Имитационная модель.
На первом этапе ищется отождествление (размещение) состояний А по В. С этой целью в соответствующем блоке модели осуществляется взятие декартова произведения графоидов А и В, т.е. находится 
. Далее выполняется процедура выделения подграфа 
графа 
, носитель которого 
определяет размещение состояний А по В. Размещение выполняется параллельно с выбором вершин принадлежащих с учётом ограничения . Если 
, то в результате будет найдено эквивалентное расширение носителя 
– 
, позволяющее найти размещение по В. Если подграф не существует, то делается вывод, что выделение заданной стандартной компоненты не возможно, на вход системы поступает следующий графоид из банка стандартных автоматов, работа модели начинается с начала. Использованный для размещения состояний автомата по заданной компоненте метод описан в [1].
Размещение состояний А по В является начальным условием для размещения по второй (искомой) компоненте (состояния совместно размещённые в первой компоненте не могут быть совместно размещены во второй компоненте разложения).
На втором этапе работы модели для определения размещения по второй компоненте, в зависимости от результата полученного на предыдущем этапе, по графоиду или строится граф сцепления 
[2]. Сигнатура расширяется введением рёбер, соединяющих вершины, соответствующие состояниям, совместно размещённым в первой компоненте. Выполняется минимальная раскраска , и тем самым определяется хроматическое число графа сцепления 
. Если 
, то полученная раскраска соответствует размещению состояний А по С. В противном случае в зависимости от величины превышения над q проектировщик определяет направление дальнейшей работы системы. Если эта величина не значительна, то выполняется сужение сигнатуры [3], и последующая его раскраска, в противном случае для определения размещения по второй компоненте используется метод, описанный в [4]. Использование этого метода предполагает нахождение множества 
, элементами которого являются множества подмножеств состояний автомата, совместное размещение которых не приведёт к неоднозначности переходов в компонентах разложения и определение размещения состояний автомата по компонентам посредством анализа этого множества. В рассматриваемой модели при нахождении множества рассматриваются только те подмножества состояний автомата А, которые не содержат пар состояний совместно размещённых по В.
И сужение сигнатуры , и нахождение осуществляется в результате совместной работы каждого из соответствующих блоков с блоком определения ограничений, которые накладывает совместное размещение определённых подмножеств состояний на размещение остальных состояний автомата. Для определения этих ограничении используется граф 
, полученный из 
[4].
Если не удаётся найти размещение А по С, то делается вывод, что искомое разложение не существует и рассматривается возможность выделения следующего автомата из банка стандартных автоматов.
Анализ результатов моделирования показывает, что для устройств промышленной автоматики реальной сложности с помощью предложенной системы можно получать их представление совокупностью стандартных компонент на абстрактном этапе проектирования за приемлемое время на ЭВМ среднего класса.
Список литературы
Дзугкоева А.А., Пагиев К.Х. Использование СП-разбиений в САПР систем логического управления. Сб. тр. СОО АНВШРФ. Владикавказ. № 5. 2007.
Горбатов В.А. Фундаментальные основы дискретной математики. М.: Наука – Физматлит, 2000.
Дзугкоева А.А. Исследование процедур расщепления запрещённых фигур раскраски графа сужением его сигнатуры. Известия высших учебных заведений Северо-Кавказский регион. Технические науки 2007, №3. Ростов-на-Дону.
Дзугкоева А.А., Дедегкаев А.Г. Размещение внутренних состояний автомата по компонентам разложения при его параллельной декомпозиции. Безопасность информационных технологий. М., 2007.