Информационно-методическое письмо об учебнике-тетради по математике для учащихся 3 класса четырехлетней начальной школы
СОДЕРЖАНИЕ: Структура программы по математике для учащихся третьего класса. Концепция построения учебного материала. Диалектические приемами формирования умственных действий: объединение, обращение, смена альтернативы, поиск связей, зависимостей и закономерностей.Авт. Жикалкина Т.К.
Настоящее пособие представляет собой комплект, состоящий из четырех тетрадей - по одной на каждую четверть.
Структура программы для учащихся третьего класса построена в соответствии с ранее изложенной концепцией построения учебного материала, в соответствии с диалектическими приемами формирования умственных действий: объединение, превращение, обращение, смена альтернативы, поиск связей, зависимостей и закономерностей. Все взаимосвязанные вопросы объединены в блоки и изучаются на основе сравнения.
В программе функционируют основные содержательные линии курса математики - понятие числа, арифметические действия, преобразование, функциональная пропедевтика, величины, задачи, алгебраическая и геометрическая пропедевтика.
В учебнике математики для третьего класса создана ориентировочная основа для деятельности учащихся. Построение учебника математики на деятельностной основе повышает активность ученика в процессе обучения, интенсивность труда учащихся и ускоряет процесс обучения.
В основном учебник математики для учащихся 3-го класса соответствует действующей программе по математике четырехлетней начальной школы.
Однако в программу третьего класса внесены некоторые изменения. Так, в раздел Табличные умножение и деление включено изучение распределительного свойства умножения и деления (правило умножения и деления суммы на число), что позволит более глубоко и сознательно изучить табличное умножение и деление. Например, ученик забыл случай умножения числа 8 на 6, но он помнит прием умножения 5 на 6 и 3 на 6.
Представив число 8 в виде суммы удобных слагаемых (5+3), ученик умножает сумму:
(5 + 3) на 6 : (5 + 3) . 6 = 5 . 6 + 3 . 6 = 30 + 18 = 48.
Аналогично ученик применяет распределительное свойство деления суммы на число. Например, ученик затрудняется выполнить прием деления 72 на 8. Представив делимое 72 в виде суммы удобных слагаемых (40 и 32), ученик без усилий найдет результат деления:
72 : 8 = (40 + 32) : 8 = 40 : 8 + 32 : 8 = 5 + 4 = 9
При изучении вычитания трехзначных чисел вводятся правила вычитания числа из суммы и суммы из числа. Эти правила вводятся при изучении приемов вычитания вида: 965 - 300; 876 - 356. При рассмотрении первого вычислительного приема удобно уменьшаемое представить в виде суммы разрядных слагаемых и вычесть число из суммы:
965 - 300 = (900 + 60 + 5) = (900 - 300) + 60 + 5 = 665.
При рассмотрении второго вычислительного приема 876-356 целесообразно вычитаемое представить в виде суммы разрядных слагаемых и вычесть из числа сумму:
876 - 356 = 876 - (300 + 50 + 6) = 876 - 300 - 50 - 6 = 520.
При изучении геометрического материала наряду с параллельными и пересекающимися линиями, рассмотренными во втором классе, в третьем классе вводятся перпендикулярные линии, которые ученики наблюдают ежедневно в клетчатой тетради. Необходимость изучения перпендикулярных линий связана с изучением прямых углов, которые образуются при пересечении перпендикулярных линий.
Сложный раздел геометрического материала Площадь и ее измерения распределяется на два года обучения - третий и четвертый. При изучении этого раздела ученики допускают много ошибок, смешивая площадь и периметр. Поэтому эти разделы математики изучаются на основе сопоставления и противопоставления.
Изучение чисел в пределах 1000 позволяет включить в программу третьего класса следующие величины: из мер длины - километр, из мер массы - центнер и тонну, из мер площади - кв.см, кв.дм, кв.м.
Из алгебраического материала наряду с простейшими уравнениями вида: 560 + х = 940, 850 - х = 620, х - 350 = 750, 420 : х = 7,
х . 6 = 420, х : 7 = 8, в программу третьего класса включены составные уравнения вида:
х . 6 : 3 + 150 = 25 . 10, решаемые путем преобразования их в цепочку взаимосвязанных простых уравнений. Например:
х . 6 : 3 + 150 = 25 . 10
![]()
Осознав, что каждая свободная клетка обозначает неизвестный компонент действия и что для его нахождения нужно 2 числа, и что они известны только в последнем уравнении, учащиеся начинают решать его с последнего действия, двигаясь при решении составного уравнения справа налево. Записывая составное уравнение в виде цепочки простых уравнений, ученики приходят ко второму выводу, что при решении составного уравнения неизвестный компонент последнего простого уравнения равен результату предыдущего уравнения, а неизвестный компонент второго уравнения равен результату третьего уравнения, считая справа налево:
![]()
Поэтому в дальнейшем схема упрощается:
![]()
Заполняя свободные клетки справа налево, учащиеся в каждом уравнении находят неизвестный компонент действия, приемы нахождения которых изучены во втором классе.В дальнейшем прием решения составных уравнений закрепляется в игре ЭВМ, в которой один ученик выполняет роль ЭВМ, а второй - роль контролера.
Например:
включи уравнение в программу ЭВМ и реши его:
а . 6 : 4 + 210 = 30 . 10

| Проверка: | 1) 300 - 210 = 90 |
| 2) 90 . 4 = 360 | |
| 3) 360 : 6 = 60 | |
| 4) 60 . 6 : 4 + 210 = 300. |
В программу третьего класса включены сюжетные задачи с прозрачной зависимостью, решаемые на основе составления уравнений, а также буквенные выражения и запись свойств действия в общем виде.
Приведем систему заданий по различным разделам программы, построенную в соответствии с формированием диалектических приемов умственных действий и основными понятиями, включенными в программу математики для третьего класса.
I. Табличные умножение и деление
Приведем систему заданий при изучении табличного умножения и деления на примере изучения таблицы умножения и деления на 7.
1. Составь по рисунку таблицу сложения, умножения и деления на 7.
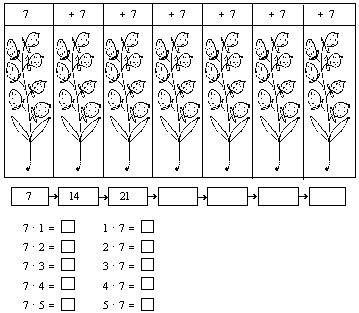
и т.д.
2. Сравни значения произведений в таблицах умножения и определи, на сколько каждое следующее произведение больше предыдущего.
3. Запиши множители следующих произведений:
![]()
4. Вычисли произведения и частные:
![]()
5. Определи правило, по которому составлены ряды чисел и запиши его в виде буквенного выражения. Продолжи второй ряд чисел:
![]()
6. Составь равенства с числами по образцу:
2, 7, 14; 8, 7, 56; 9, 7, 63; 9, 8, 72
2 . 7 = 14 14 = 2 . 7 14 : 7 = 2
7 . 2 = 14 14 : 2 = 7
7. Определи правило, по которому составлены ряды чисел, впиши в свободные клетки соответствующие числа:
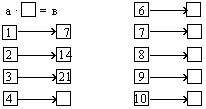
8. Определи закономерность, по которой составлен данный числовой ряд. Запиши правило составления этого числового ряда с использованием букв.
| а - предыдущее число | } a ... |
| в - следующее число |
Впиши в клетки соответствующие числа:
![]()
На сколько больше каждое следующее число предыдущего?
Назови множители чисел: 7, 14, 21..., один из которых число 7.
9. Сравни ряды чисел по строчкам и столбцам. Сделай выводы. Если множитель увеличивается в несколько раз, то произведение... во столько же раз. Если множитель уменьшается в несколько раз, то произведение... во столько же раз.

10. Реши уравнения:
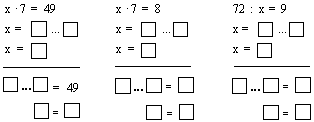
11. Заполни свободные клетки и объясни правила нахождения неизвестных компонентов действий:
![]()
12. Вычисли и объясни, какое правило использовал при вычислении:
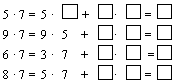
13. Поставь соответствующие знаки между выражениями:
![]()
14. Замени неравенства равенствами:
![]()
15. Составь цепочки взаимосвязанных числовых равенств по равенству, заданному в общем виде (с использованием букв): а . в = с,
| если | а = 7, в = 9, с = 63; |
| а = 7, в = 9, с = 63;а = 7, в = 8, с = 56 и т.д. | |
| а . в = с, в . а = с, с . а = в, с : а = в, с : в = а. |
II. Площадь. Единицы площади
Раскроем фрагменты методики изучения этой темы:
1. Сравни фигуры по размеру. Какая фигура больше - прямоугольник или квадрат? Квадрат или круг? Сделай выводы:

2. Сравни площадь доски и пола, площадь стола и обложки книги. Сделай вывод: если площадь пола ... площади доски, а площадь доски ... больше площади обложки книги, то площадь пола ... площади обложки книги.
3. Из разрезанного квадрата составлены условные рисунки кошки, домика, зайца. Сравни площадь квадрата и каждого рисунка, составленного из квадрата. Какие это площади? (Дать рис.)
4. Какой из углов больше, какой меньше? Проверь по модели прямого угла:

5. Если острый угол,.. чем прямой, а прямой,.. чем тупой, то острый угол,.. чем тупой.
6. Измерь отрезки и сравни их по длине?
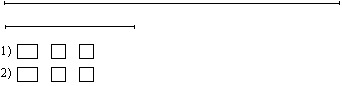
7. Вы научились сравнивать углы и отрезки. Необходимо научиться сравнивать и измерять площади геометрических фигур комнат, участков земли
Единицами измерения длины являются линейные меры: см, дм, м.
Площадь измеряют квадратными единицами: квадратным сантиметром, квадратным дециметром, квадратным метром. Их сокращенно обозначают так: см2 , дм2 , м2 .
Это линейный сантиметр Это квадратный сантиметр
![]()
8. Измерь стороны этого прямоугольника:
| Положи на него по длине квадратные сантиметры. Сколько квадратных сантиметров поместилось по длине? Положи и во втором ряду квадратные сантиметры. Сколько квадратных сантиметров разместилось во втором ряду? Сколько всего квадратных сантиметров разметилось на площади этого прямоугольника? Как узнал? Объясни. | |
| 4 . 2 = 8 (см2 ). Вспомни, чему равны длина и ширина этого прямоугольника. 8 см2 - это произведение каких чисел? Итак, мы узнали, что площадь прямоугольника равна 8 см2. | |
9. Какие фигуры изображены на этом чертеже? Вычисли площади этих фигур. Сравни их:
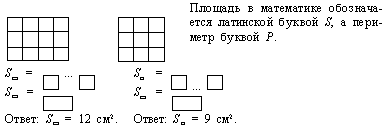
Сравни ответ с длиной и шириной этих фигур. Каким действием узнали площадь этих фигур?
10. Какие фигуры изображены на этом чертеже? Измерь длину и ширину каждой фигуры. Вычисли площадь каждой фигуры. Сравни их:
 |
Сколько квадратных сантиметров разместилось по длине каждой фигуры? По ширине? Сколько всего квадратных сантиметров разместилось на площади каждой фигуры. Сравни результат с длиной и шириной и сделай вывод, как найти площадь этих фигур? Сравни их:
|
11. Какие фигуры изображены на этом чертеже? Сколько квадратных сантиметров разместилось на этом чертеже? Сколько таких рядов разместится на каждой фигуре? Вычисли площадь каждой фигуры. Сравни их:
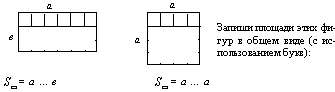
12. Какие фигуры представлены на этом чертеже? Соедини точки, изображенные на сторонах этих фигур, отрезками (по вертикали и горизонтали). Сначала запиши площади этих фигур в общем виде и вычисли их:
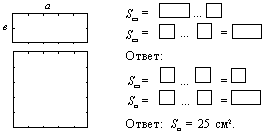
| 13. |
|
14. Сравни, как вычисляются периметр и площади фигур. Вычисли их и запиши в таблице. Сравни единицы измерения периметра и площади
| ? п/п | Длина | Ширина | Периметр Р = 2а + 2в |
Площадь S = а . в |
| 1. | Длина прямоугольника 6 см | Ширина 4 см | ||
| 2. | Сторона квадрата 7 см | |||
| 3. | Длина прямоугольника 8 см | Ширина 6 см |
15. Измерь длину и ширину доски. Какой единицей удобно измерить длину и ширину доски?
16. Какова длина этого отрезка?
![]()
Сколько линейных сантиметров в одном линейном дециметре?
17. Как измерить площадь доски? Какую единицу измерения удобно выбрать? 18. Раздели квадрат, сторона которого равна 1 дм на квадратные сантиметры. Сколько квадратных сантиметров поместилось на одном квадратном дециметре? В одном линейном дециметре 10 линейных сантиметров. 1 дм = 10 см В одном квадратном дециметре 100 см2 1 дм2 = 100 см2 |
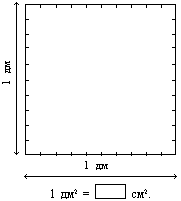 |
19. Вычисли площадь классной доски с помощью дециметра:
![]()
20. Какие единицы целесообразно применить для измерения огорода, сада, небольшого земельного участка?
В одном линейном метре 10 линейных дециметров. 1 м = 10 дм |
В одном квадратном метре 100 квадратных дециметров. 1 м2 = 100 дм2 |
21. Вырежь из бумаги 1 см2 , 1 дм2 , 1 м2 .
22. Вырежь из бумаги два квадрата со стороной 7 см. Какие площади у этих квадратов?
23. Вычисли площадь кровельного железа, если длина его 12 дм, а ширина 7 дм.
![]()
24. Найди площадь земельного участка со стороной 6 м. Вычисли периметр этого участка. Сравни, как узнали площадь и периметр этого участка?
![]()
25. Начерти в дополнительной тетради прямоугольник со сторонами 7 и 6 см и квадрат со стороной 7 см. Определи их площадь. Узнай, площадь какой фигуры больше и на сколько?
![]()
26. Длина прямоугольного участка 15 м, а ширина 6 м. Вычисли его площадь и периметр. Сравни их:
![]()
27. Площадь квадратного участка 100 м2. Определи периметр этого участка. Начерти чертеж к задаче и реши ее в дополнительной тетради.
28. Составь задачи по чертежу и числовым данным и реши их:
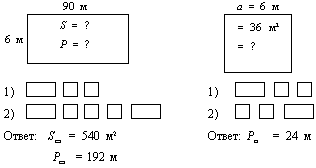
29. Длина участка прямоугольной формы 90 м, ширина составляет 1 /10 часть от длины. 1 /3 всей площади занята капустой, остальная часть - картофелем. Какая площадь занята картофелем? Построй чертеж в дополнительной тетради и реши ее.
30. 1 /3 участка прямоугольной формы засажена капустой, что составляет 270 м2 , остальная часть участка занята картофелем. Какая площадь занята под картофель? Построй чертеж в дополнительной тетради и реши ее.
31. Определи, как изменяется площадь от увеличения или уменьшения длины ее сторон:
| ? п/п | Длина участка | Ширина участка | Площадь участка |
| 1. | 50 м | 10 м | |
| 2. | 100 м | 10 м | |
| 3. | 10 м | 10 м | |
| 4. | 50 м | 20 м | |
| 5. | 50 м | 5 м |
Если длина одной из сторон увеличивается в несколько раз, то площадь ... во столько же раз. Если длина одной из сторон уменьшается в несколько раз, то площадь ... во столько же раз.
III. Составные уравнения
С простейшими уравнениями вида: х + 35 = 70, 60 - х = 32,
х - 15 = 46, х . 3 = 27 и приемами их решения учащиеся познакомились еще во втором классе. Поэтому в третьем классе вводятся составные уравнения вида:
х : 7 . 9 + 250 = 340
Учащиеся решают составные уравнения на основе знания взаимосвязи между компонентами и результатами действий. Главное затруднение для учащихся третьего класса при решении уравнений этого вида - назвать неизвестный компонент действия, который выражен еще двумя, тремя простыми уравнениями. Например, при решении уравнения вида: х : 7 . 9 + 250 = 340 ученик должен рассуждать так: Последнее действие - сложение. Неизвестно слагаемое. Ученику сложно понять, что х : 7 . 9 - это слагаемое, поэтому для решения составного уравнения предлагается прием преобразования составного уравнения в цепочку взаимосвязанных простых уравнений вида:
х : 7 . 9 + 250 = 340.
Учитель спрашивает: Сколько действий в этом уравнении?. (Три).
Запишем отдельно в каждом прямоугольнике компоненты каждого действия:
![]()
Сколько простых уравнений в составном? (Три.)
Почему оставлены свободные клетки? (Потому, что неизвестны компоненты этих действий).
Чтобы решить простое уравнение, сколько чисел надо знать? (Два).
В каком уравнении известны два числа? (В последнем).
С последнего действия и начнем решать уравнение.
Какой компонент действия неизвестен? (Первое слагаемое).
Как его найти? (Надо из суммы вычесть известное слагаемое).
Чему равно неизвестное слагаемое? (340 - 250 = 90).
Запишите его в свободной клетке последнего уравнения.
Перейдем к решению следующего уравнения. Прочитайте его: неизвестное число умножить на 9, получится ... (90).
Запишите его в свободной последней клетке второго уравнения, считая справа налево.
Что неизвестно в этом уравнении? (Первый множитель).
Как его найти? (Надо произведение 90 разделить на второй множитель 9, получится 10).
Запишите полученное число в свободной клетке второго уравнения. Какое число получится? (10).
Прочитайте третье уравнение, считая справа налево. (Неизвестное число разделить на 7, получится 10).
Запишите число 10 в последней клетке третьего уравнения, считая справа налево.
Что неизвестно в этом уравнении? (Делимое).
Как найти неизвестное делимое? (Надо частное 10 умножить на делитель 7, получится делимое 70).
Проверим решение всего уравнения:
(70 : 7 = 10, 10 . 9 = 90, 90 + 250 = 340)
Как решили составное уравнение? (Правильно).
Что вы можете рассказать о составном уравнении? (Оно состоит из простых уравнений.)
Как они взаимосвязаны? (Ответ предыдущего уравнения, считая слева направо, равен первому компоненту следующего уравнения.)
В дальнейшем схема решения уравнения упрощается и записывается так:
![]()
При решении уравнений используются игры: Вычислительная машина, Цепочка.
В игре Вычислительная машина один ученик выполняет роль ЭВМ (решает уравнение), а другой - выполняет роль контролера - проверяет решение каждого уравнения и всего уравнения в целом. Например:
Включи уравнение в программу ЭВМ и реши его:
с . 2 : 5 - 150 = 25 . 2
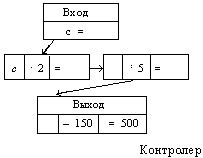
Проверка:
1) 150 + 50 = 200
2) 200 . 5 = 1000
3) 1000 : 2 = 500
500 . 2 : 5 - 150 = 50
В дальнейшем проводится игра Цепочка, в которой запись уравнения представлена кружками, а результаты прохождения неизвестных компонентов действий - прямоугольниками.
Например:
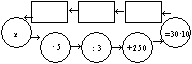
При обучении решению уравнений вводятся задачи вида:
1. Рита задумала число, увеличила его в 6 раз, результат уменьшила в 3 раза и к полученному числу прибавила 160, получила 300.
2. Витя спросил Сережу: Какую оценку ты получил по математике?. А вот угадай сам. Если полученное число баллов увеличить
в 9 раз, а затем уменьшить в 3 раза и прибавить к результату число 150, то получится 165. Какую оценку получил Сережа?