Интегральная атака против блочного симметричного шифра Crypton

СОДЕРЖАНИЕ: Основные требования к блочным симметричным шифрам как к механизмам, обеспечивающим конфиденциальность. Адаптация методики реализации интегральной атаки для расшифрования усеченного варианта Crypton. Использование криптографических способов защиты.

ВВЕДЕНИЕ

Стремительное развитие современных информационных технологий в Украине, начавшееся в конце XX века, не снижает своих темпов и в начале XXI века. Компьютерные технологии оказывают все большее влияние на все сферы человеческой деятельности. Постоянное увеличение скорости и объема передаваемых в информационных системах данных повышает эффективность производственных процессов, способствует расширению деловых операций.

Именно поэтому ужесточаются требования к информационной безопасности. Под ней понимается защищенность информации и поддерживающей инфраструктуры от случайных и преднамеренных воздействий, которые могут нанести ущерб владельцам или пользователям информации. Обеспечение безопасности информационной системы является одной из важнейших задач при эксплуатации данной системы, так как от сохранения конфиденциальности, целостности и доступности информационных ресурсов во многом зависит быстрота принятия решений, эффективность и надежность работы [1] . Разработка и анализ блочных шифров, является очень актуальной и необходимой задачей, которая должна быть реализована на государственном уровне, поскольку от этого зависит государственная безопасность Украины. Украине необходимо иметь свой БСШ.

Одним из основополагающих элементов в общем комплексе средств и методов обеспечения информационной безопасности являются криптографические методы защиты информации[2]. На данном этапе развития применяется как симметричные, так и несимметричные криптографические методы защиты. Это обуславливается тем, что первые способны обеспечить высокую скорость шифрования, а вторые – модель взаимного недоверия и защиты, т.е. ситуацию, когда пользователи информационных систем не хотят никому доверять свои личные ключи и параметры, но при этом хотят иметь гарантию компенсации потерь, если их обманут.

Широкое использование симметричной криптографии определяет необходимость исследования стойкости симметричных шифров к существующим методам криптоанализа.

Одним из наиболее эффективных, на сегодняшний день, является интегральный метод криптоанализа.

Целью данной работы является изучение теоретических основ и реализация интегральной атаки на практике для усеченной модели блочного симметричного шифра Сrypton, а также изучение особенностей и ограничений применения атаки.

Для достижения этой цели необходимо решить следующие задачи:

- Изучить методику применения интегральной атаки против блочного симметричного шифра Crypton.

- Адаптировать методику применения интегральной атаки для использования против усеченного варианта блочного симметричного шифра Crypton.

- Выполнить программнуюреализацию интегральной атаки против усеченного вариантаблочного симметричного шифра Crypton.

В данной дипломной работе рассчитывается экономическая эффективность разработки методикиопределения стойкости блочного симметричного шифра Сryptonпротивинтегральной атаки.

В разделе Безопасность жизнедеятельности дипломного проекта необходимо разработать вопросы БЖД при выполнении работ по разработке интегральной атаки на шифр Crypton, которые выполняются в научно-исследовательской лаборатории (НИЛ). В разделе следует выполнить анализ условий труда, разработать вопросы техники безопасности, производственной санитарии и гигиены труда, пожарной профилактики.

1. БЛОЧНЫЕ СИММЕТРИЧНЫЕ ШИФРЫ И ИХ МЕСТО В СОВРЕМЕННЫХ ИНФОРМАЦИОННЫХ СИСТЕМАХ

1.1 Основные требования к БСШ как к механизму обеспечивающему конфиденциальность

На сегодняшний день разработано достаточно много стойких блочных шифров. Практически все алгоритмы используют для преобразований определенный набор биективных (обратимых) математических преобразований.

Характерной особенностью блочных криптоалгоритмов является тот факт, что в ходе своей работы они производят преобразование блока входной информации фиксированной длины и получают результирующий блок того же объема, но недоступный для прочтения сторонним лицам, не владеющим ключом. Таким образом, схему работы блочного шифра можно описать функциями

Z=EnCrypt(X,Key) и X=DeCrypt(Z,Key)[3]

Ключ Key является параметром блочного криптоалгоритма и представляет собой некоторый блок двоичной информации фиксированного размера. Исходный (X) и зашифрованный (Z) блоки данных также имеют фиксированную разрядность, равную между собой, но необязательно равную длине ключа.

Блочные шифры являются основой, на которой реализованы практически все криптосистемы[4]. Методика создания цепочек из зашифрованных блочными алгоритмами байт позволяет шифровать ими пакеты информации неограниченной длины. Такое свойство блочных шифров, как быстрота работы, используется асимметричными криптоалгоритмами, медлительными по своей природе. Отсутствие статистической корреляции между битами выходного потока блочного шифра используется для вычисления контрольных сумм пакетов данных и в хешировании паролей.

Стойкость криптоалгоритмов описана в [5], [6]. Криптоалгоритм именуется идеально стойким, если прочесть зашифрованный блок данных можно только перебрав все возможные ключи, до тех пор, пока сообщение не окажется осмысленным. Так как по теории вероятности искомый ключ будет найден с вероятностью 1/2 после перебора половины всех ключей, то на взлом идеально стойкого криптоалгоритма с ключом длины N потребуется в среднем 2N-1 проверок. Таким образом, в общем случае стойкость блочного шифра зависит только от длины ключа и возрастает экспоненциально с ее ростом. Даже предположив, что перебор ключей производится на специально созданной многопроцессорной системе, в которой благодаря диагональному параллелизму на проверку 1 ключа уходит только 1 такт, то на взлом 128 битного ключа современной технике потребуется не менее 1021 лет. Естественно, все сказанное относится только к идеально стойким шифрам, которыми, например, с большой долей уверенности являются приведенные в таблице выше алгоритмы.

Кроме этого условия к идеально стойким криптоалгоритмам применяется еще одно очень важное требование, которому они должны обязательно соответствовать. При известных исходном и зашифрованном значениях блока ключ, которым произведено это преобразование, можно узнать также только полным перебором. Ситуации, в которых постороннему наблюдателю известна часть исходного текста встречаются повсеместно. Это могут быть стандартные надписи в электронных бланках, фиксированные заголовки форматов файлов, довольно часто встречающиеся в тексте длинные слова или последовательности байт. В свете этой проблемы описанное выше требование не является ничем чрезмерным и также строго выполняется стойкими криптоалгоритмами, как и первое.

Таким образом, на функцию стойкого блочного шифра Z=EnCrypt(X,Key) накладываются следующие условия:

- функция EnCrypt должна быть обратимой.

- не должно существовать иных методов прочтения сообщения X по известному блоку Z, кроме как полным перебором ключей Key.

- не должно существовать иных методов определения каким ключом Key было произведено преобразование известного сообщения X в сообщение Z, кроме как полным перебором ключей.

Давайте рассмотрим методы, с помощью которых разработчики блочных криптоалгоритмов добиваются одновременного выполнения этих трех условий с очень большой долей достоверности. Все действия, производимые над данными блочным криптоалгоритмом, основаны на том факте, что преобразуемый блок может быть представлен в виде целого неотрицательного числа из диапазона, соответствующего его разрядности. Так, например, 32-битный блок данных можно интерпретировать как число из диапазона 0..4294967295. Кроме того, блок, разрядность которого обычно является степенью двойки, можно трактовать как несколько независимых неотрицательных чисел из меньшего диапазона (рассмотренный выше 32-битный блок можно также представить в виде 2 независимых чисел из диапазона 0..65535 или в виде 4 независимых чисел из диапазона 0..255). Над этими числами блочным криптоалгоритмом и производятся по определенной схеме показаной на Таб 1.1 (слева даны условные обозначения этих операций на графических схемах алгоритмов):

В качестве параметра V для любого из этих преобразований может использоваться:

- фиксированное число (например, X=X+125)

- число, получаемое из ключа (например, X=X+F(Key))

- число, получаемое из независимой части блока (например, X2=X2+F(X1))

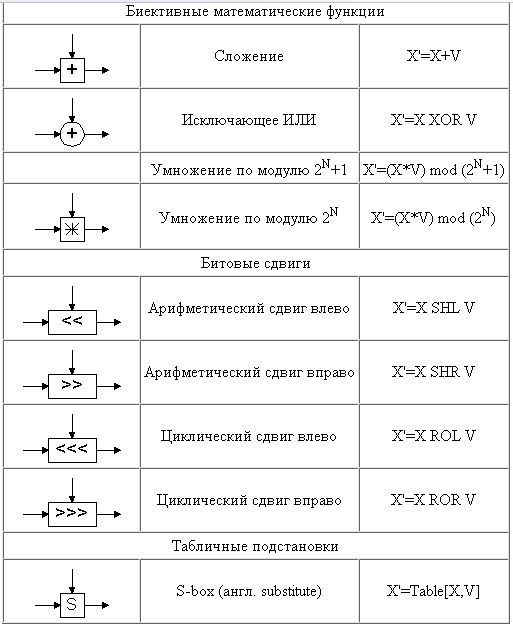
Таблица 1.1 Условные обозначения операций на графических схемах алгоритмов.

Последний вариант используется в схеме, названной по имени ее создателя сетью Фейстеля (нем. Feistel).

Последовательность выполняемых над блоком операций, комбинации перечисленных выше вариантов V и сами функции F и составляют ноу-хау каждого конкретного блочного криптоалгоритма. Размер блоков и длина ключа современных (1999 год) алгоритмов были нами рассмотрены ранее. Один-два раза в год исследовательские центры мира публикуют очередной блочный шифр, который под яростной атакой криптоаналитиков либо приобретает за несколько лет статус стойкого криптоалгоритма, либо (что происходит неизмеримо чаще) бесславно уходит в историю криптографии.

Характерным признаком блочных алгоритмов является многократное и косвенное использование материала ключа. Это диктуется в первую очередь требованием невозможности обратного декодирования в отношении ключа при известных исходном и зашифрованном текстах. Для решения этой задачи в приведенных выше преобразованиях чаще всего используется не само значение ключа или его части, а некоторая, иногда необратимая (небиективная) функция от материала ключа. Более того, в подобных преобразованиях один и тот же блок или элемент ключа используется многократно. Это позволяет при выполнении условия обратимости функции относительно величины X сделать функцию необратимой относительно ключа Key.

Поскольку операция зашифровки или расшифровки отдельного блока в процессе кодирования пакета информации выполняется многократно (иногда до сотен тысяч раз), а значение ключа и, следовательно, функций Vi(Key) остается неизменным, то иногда становится целесообразно заранее однократно вычислить данные значения и хранить их в оперативной памяти совместно с ключом. Поскольку эти значения зависят только от ключа, то оин в криптографии называются материалом ключа. Необходимо отметить, что данная операция никоим образом не изменяет ни длину ключа, ни криптостойкость алгоритма в целом. Здесь происходит лишь оптимизация скорости вычислений путем кеширования (англ. caching) промежуточных результатов. Описанные действия встречаются практически во многих блочных криптоалгоритмах и носят название расширение ключа (англ. key scheduling)

1.2 Обзор известных БСШ

1.2.1 Анализ симметричного блочного шифра Rijndael

Шифр реализует совершенно нетрадиционную криптографическую парадигму, полностью отказавшись от сети Фейстела[7],[8]. К достоинствам алгоритма относят: очень хорошее быстродействие на всех платформах от 8-битных до 64-битных, самый высокий потенциальный параллелизм среди претендентов, минимальные требования к ресурсам оперативной и постоянной памяти в реализации без кеширования некоторых операций, устойчивость к подавляющему большинству атак по времени исполнения и потребляемой мощности, структура шифра позволяет использовать любые комбинации размеров блока и длин ключа, кратные 32 бит (при достижении размером блока определенных границ требуется только увеличение числа раундов). При этом процедуры шифрования/дешифрования и операции расширения ключей различаются между собой достаточно сильно по сравнению с простым изменением порядка ключей либо операцией наложения, характерных для сети Фейстела, что увеличивает суммарный объем кода алгоритма.

Как показали предварительные исследования [9],[10], Rijndael может быть очень эффективно реализован на самых разных процессорах и чрезвычайно успешно противостоит известным криптоаналитическим атакам.

Rijndael представляет собой итеративный блочный шифр, имеющий переменную длину блоков и различные длины ключей. Длина ключа и длина блока могут быть независимо друг от друга 128, 192 или 256 бит.

Разнообразные преобразования работают с промежуточным результатом, называемым Состоянием (State).

Состояние можно представить в виде прямоугольного массива байтов. Этот массив имеет 4 строки, а число столбцов обозначено как Nb и равно длине блока, деленной на 32.

Ключ шифрования также представлен в виде прямоугольного массива с четырьмя строками. Число столбцов обозначено как Nk и равно длине ключа, деленной на 32. Это показано на рисунке 1.4.

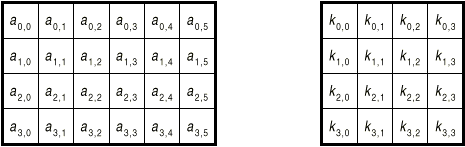
Рисунок 1.4. Пример представления Состояния (Nb=6) и Ключа шифрования (Nk=4).

В некоторых случаях ключ шифрования показан как линейный массив 4-байтовых слов. Слова состоят из 4 байтов, которые находятся в одном столбце (при представлении в виде прямоугольного массива) как показано на рисунке 1.4 взятый с [11].

Входные данные для шифра (открытый текст, если используется режим шифрования ECB) обозначаются как байты состояния в порядке a0,0, a1,0, a3,0, a0,1, a1,1, a3,1 ,a4,1 ... После завершения действия шифра выходные данные получаются из байтов состояния в том же порядке.

Число циклов обозначено как Nr и зависит от значений Nb и Nk. Оно приведено в Таблице 1.2

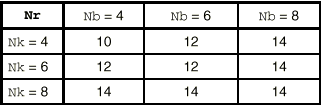
Таблица 1.2 Число циклов (Nr) как функция от длины ключа и длины блока.

Цикловое преобразование состоит из четырех различных преобразований. На псевдо-Си это выглядит следующим образом:

Round (State, RoundKey)

{

ByteSub(State); // замена байт

ShiftRow(State); // сдвиг строк

MixColumn(State); // замешивание столбцов

AddRoundKey(State, RoundKey); // добавление циклового ключа

}

Последний цикл шифра немного отличается. Вот как он выглядит:

FinalRound(State, RoundKey)

{

ByteSub(State); // замена байт

ShiftRow(State); // сдвиг строк

AddRoundKey(State, RoundKey); // добавление циклового ключа

}

В приведенной записи, функции - Round, ByteSub и т.д. выполняют свои действия над массивами, указатели (т.е. State, RoundKey) на которые им передаются.

Как можно заметить, последний цикл отличается от простого цикла только отсутствием замешивания столбцов. Каждое из приведенных преобразований разобрано далее.

Преобразование ByteSub представляет собой нелинейную замену байт, выполняемую независимо с каждым байтом состояния. Таблицы замены (или S-блоки) являются инвертируемыми и построены из композиции двух преобразований:

1. Первое - получение обратного элемента относительно умножения в поле GF(28), 00 переходит сам в себя.

2. Применение афинного преобразования (над GF(2)), определенного как:

Табл. 1.3. Таблицы замены

Применение описанного S-блока ко всем байтам состояния обозначено как ByteSub(State). Рисунок 1.5 иллюстрирует применение преобразования ByteSub к состоянию.

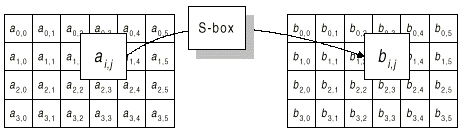
Рисунок 1.5 ByteSub действует на каждый байт состояния.

Последние 3 строки состояния циклически сдвигаются на различное число байт. Строка 1 сдвигается на С1 байт, строка 2 - на С2 байт и строка 3 - на С3 байт. Значения сдвигов С1, С2 и С3 зависят от длины блока Nb. Их величины приведены в таблице 1.4.

Таблица 1.4. Величина сдвига для разной длины блоков.

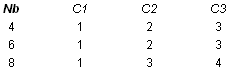
Операция сдвига последних 3 строк состояния на определенную величину обозначена как ShiftRow(State). Рисунок 1.5 показывает влияние преобразования на состояние.

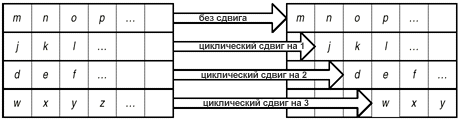
Рисунок 1.5 ShiftRow действует на строки состояния.

В преобразовании замешивания столбцов (MixColumn) столбцы состояния рассматриваются как многочлены над GF(28) и умножаются по модулю x4+1 на многочлен c(x), выглядящий следующим образом:

c(x)=03 x3 + 01 x2 + 01 x + 02(1.8)

Это может быть представлено в виде матричного умножения. Пусть b(x)=c(x)a(x),

Табл. 1.6 Матричное умножение

Применение этой операции ко всем четырем столбцам состояния обозначено как MixColumn(State). Рисунок 1.7 демонстрирует применение MixColumn к состоянию.

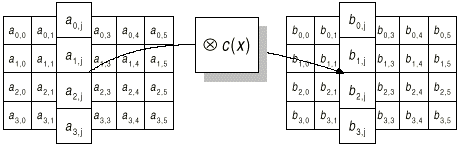
Рисунок 1.7 MixColumn действует на столбцы состояния.

В следующей операции цикловой ключ добавляется к состоянию посредством простого EXOR. Цикловой ключ вырабатывается из ключа шифрования посредством алгоритма выработки ключей (key schedule). Длина циклового ключа равна длине блока Nb.

Преобразование, содержащее добавление посредством EXOR циклового ключа к состоянию, обозначено как AddRoundKey(State, RoundKey). Оно проиллюстрированно на рисунке 1.8.

Рисунок 1.8. Добавление ключа

При добавлении ключа цикловой ключ складывается посредством EXOR с состоянием.

Цикловые ключи получаются из ключа шифрования посредством алгоритма выработки ключей. Он содержит два компонента: расширение ключа (Key Expansion) и выбор циклового ключа (Round Key Selection).

Основополагающие принципы алгоритма выглядят следующим образом:

- общее число бит цикловых ключей равно длине блока, умноженной на число циклов плюс 1 (например, для длины блока 128 бит и 10 циклов требуется 1408 бит циклового ключа).

- ключ шифрования расширяется в Расширенный Ключ (Expanded Key).

- цикловые ключи берутся из Расширенного ключа следующим образом: первый цикловой ключ содержит первые Nb слов, второй - следующие Nb слов и т.д.

Расширенный ключ представляет собой линейный массив 4-ех байтовых слов и обозначен как W[Nb*(Nr+1)]. Первые Nk слов содержат ключ шифрования.

Все остальные слова определяются рекурсивно из слов с меньшими индексами. Алгоритм выработки ключей зависит от величины Nk: ниже приведена версия для Nk равного или меньшего 6 и версия для Nk большего 6.

Для Nk6 или Nk=6 мы имеем:

KeyExpansion(CipherKey,W)

{

for (i = 0; i Nk; i++) W[i] = CipherKey[i];

for (j = Nk; j Nb*(Nk+1); j+=Nk)

{

W[j] = W[j-Nk] ^ SubByte( Rotl( W[j-1] ) ) ^ Rcon[j/Nk];

for (i = 1; i Nk i+j Nb*(Nr+1); i++)

W[i+j] = W[i+j-Nk] ^ W[i+j-1];

}

Как можно заметить, первые Nk слов заполняются ключом шифрования. Каждое последующее слово W[i] получается посредством EXOR предыдущего слова W[i-1] и слова на Nk позиций ранее W[i-Nk]. Для слов, позиция которых кратна Nk, перед EXOR применяется преобразование к W[i-1], а затем еще прибавляется цикловая константа. Преобразование содержит циклический сдвиг байтов в слове, обозначенный как Rotl, затем следует SubByte - применение замены байт.

Для Nk6 мыимеем:

KeyExpansion(CipherKey,W)

{

for (i=0; iNk; i++) W[i]=CipherKey[i];

for (j=Nk; jNb*(Nk+1); j+=Nk)

{

W[j] = W[j-Nk] ^ SubByte(Rotl(W[j-1])) ^ Rcon[j/Nk];

for (i=1; i4; i++) W[i+j] = W[i+j-Nk] ^ W[i+j-1];

W[j+4] = W[j+4-Nk] ^ SubByte(W[j+3]);

for (i=5; iNk; i++) W[i+j] = W[i+j-Nk] ^ W[i+j-1];

}

Отличие для схемы при Nk6 состоит в применении SubByte для каждого 4-го байта из Nk.

Цикловая константа независит от Nk и определяется следующим образом:

Rcon[i] = ( RC[i], 00 , 00 , 00 ),

ГдеRC[0]=01, RC[i]=xtime(Rcon[i-1])

i-ый цикловой ключ получается из слов массива циклового ключа от W[Nb*i] и доW[Nb(i+1)]. Это показано на рисунке 1.9

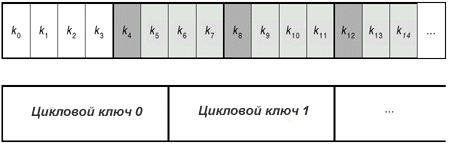
Рисунок 1.9 Расширение ключа и выбор циклового ключа для Nb=6 и Nk=4.

Алгоритм выработки ключей можно осуществлять и без использования массива W[Nb*(Nr+1)]. Для реализаций, в которых существенно требование к занимаемой памяти, цикловые ключи могут вычисляться на лету посредством использования буфера из Nk слов. Шифр Rijndael состоит из:

- Начального добавления циклового ключа;

- Nr-1 циклов;

- заключительного цикла.

На псевдо-Си это выглядит следующим образом:

Rijndael (State, CipherKey)

{

KeyExpansion(CipherKey, ExpandedKey); // Расширениеключа

AddRoundKey(State, ExpandedKey); // Добавлениецикловогоключа

For ( i=1 ; iNr ; i++) Round(State,ExpandedKey+Nb*i); // циклы

FinalRound(State, ExpandedKey+Nb*Nr); // заключительныйцикл

}

Если предварительно выполнена процедура расширения ключа, то Rijndael будет выглядеть следующим образом:

Rijndael (State, CipherKey)

{

AddRoundKey(State, ExpandedKey);

For ( i=1 ; iNr ; i++) Round(State,ExpandedKey+Nb*i);

FinalRound(State, ExpandedKey+Nb*Nr);

}

Расширенный ключ должен всегда получаться из ключа шифрования и никогда не указывается напрямую. Нет никаких ограничений на выбор ключа шифрования.

1.2.2 Анализ симметричного блочного шифра DEAL

DEAL (DataEncryptionAlgorithmwithLargerblocks - Алгоритм Шифрования Данных с Укрупненными блоками) является 128-и битным блочным шифром с размерами ключа 128, 192 и 256 бит, что далее здесь будет обозначаться DEAL-128, DEAL-192 и DEAL-256 соответственно [12]. Все версии могут использоваться в любом из четырех стандартных режимах DESa. Мы начнем с описания работы DEAL в режиме ECB. Пусть С = Е_В (А) означает зашифрованное DES значение 64-х битного А на ключе В, и пусть Y = EA_Z (X) означает зашифрование DEAL 128-и битного X на ключе Z. Открытый текст Р разделяется на блоки Pi по 128 бит каждый, P = P₁ , P₂ , …, Р_n . Расписание ключей принимает ключ К и возвращает r ключей DESRK_i , где i = 1, … , r, как описано ниже. Обозначим X^L и X^R левую и правую части X соответственно. Шифр-текст вычисляется следующим образом. Положим X₀ ^L = P_i ^L , X₀ ^R = Р_i ^R и вычислим для j= 1, … ,r

X_j ^L =E_RKj (X^L _j _-1 ) X^R _j _-1 (1.9)

X^R _j = X^L _j _-1 (1.10)

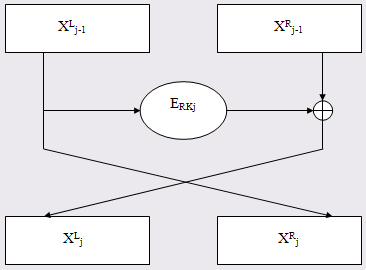
Рисунок 1.10: ОдинциклDEAL.

ПоложимC_i =X_r ^L ||X_r ^R . На рис. 1.10 показан один цикл DEAL. Для DEAL-128 и DEAL-192 мы предлагаем использовать 6 циклов, т. е. r = 6. Однако, как мы увидим ниже, этого может быть недостаточно для DEAL-256, здесь предлагается использовать 8 циклов, r = 8. Представляется, что версия с размером ключа 256 бит используется только когда требуется особенно сильное зашифрование.

Заметим, что последнем цикле DEAL половины блока местами меняются[13]. Причина в следующем: правая часть шифр-текста С_i не шифруется в последнем цикле i-oro зашифрования, и только левая часть входа i + 1-ого зашифрования (который равен C_i P_i ₊ _l ) шифруется на последнем цикле. Т. о. правая часть Ci осталась бы не перезашифрованной два цикла. Это может дать поле деятельности злоумышленникам, тем более, что шифр состоит всего из 6-и или 8-и циклов. Заметим, что аналогичное свойство есть и у DES в режиме CBC. Правда, похоже это труднее было бы использовать, ведь у DES 16 циклов. Позволим себе отметить, что обмен местами правой и левой частей на последнем цикле не влияет на стойкость блочного шифра в режиме ECB [14].

Итак, обозначим блоки открытого текста по 128 бит P₁ , P₂ , …, P_n и C_i , С₂ , ,… , С_п -соответствующие им блоки шифр-текста. Тогда:

С_i = EA_K (C_i _- _l P_i ),(1.11)

где С₀ - начальное значение.

В DES начальная перестановка IP первой применяется к открытому тексту, и аналогично перед выходом шифр-текст пропускается через обратную к ней IP^-1 . Возможно увеличить скорость DEAL, если убрать из используемого DESэти начальную и конечную перестановки. Легко показать, что для получения корректной реализации DEAL, IP должна быть приложена к обоим частям открытого текста перед зашифрованием, aIP^-1 - к обоим частям шифр-текста.

На вход расписания ключей подается s ключей DES, Ki, ,… , K_s , для s = 2, 3, 4, каждый по 64 бит (включая 8 проверочных бит, старших бит каждого байта), на выходе получается r ключей DES, RK_j . Мы используем общий метод, приложимый ко всем трем размерам ключа. Во-первых расширяем s ключей до r ключей, путем повторения и с новой константой для каждого нового повторения. Зашифровываем расширенный список ключей DESom в режиме CBC с фиксированным ключом и нулевым начальным значением. Из полученных блоков шифр-текста и формируются подключи RKi. Далее мы приводим точные определения каждого из расписаний ключей, здесь К = 0x1234 5678 90abcdefx (шестнадцатеричное число) - фиксированный ключ DES. В DEAL-128 подключи генерируются следующим образом:

RK₁ = E_K (К₁ ),

RK₂ = E_K (К₂ RK₁ ),

RK₃ =E_K (K_l (1)RK₂ ),

RK₄ = E_K (К₂ (2)RK₃ ),

RK₅ =E_k (k_i (4)RK₄ ),

RK₆ =E_k (k₂ (8)RK₅ ),(1.12)

где (i) - 64-х битное целое число, в котором i - 1-ый бит (индексация идет с 0) установлен, а остальные очищены. Например, (1) может быть представлено как шестнадцатеричное 0x8000 0000 0000 0000_х .

В DEAL-192 подключи генерируются следующим образом:

RK₁ = E_K (К₁ ),

RK₂ = E_K (К₂ RK₁ ),

RK₃ =E_K (K₃ RK₂ ),

RK₄ =E_k (k_i (1)RK₃ ),

RK₅ =E_k (k₂ (2)RK₄ ),

RK₆ =Е_К (К₃ (4)RK₅ ).(1.13)

Эти версии расписания ключей требуют 6 расписаний ключей DES и 6 зашифрований DES на фиксированном ключе. Подключи нужно сгенерировать только один раз, если их впоследствии сохранить.

В DEAL-256 подключи генерируются следующим образом:

RK₁ = E_K (К₁ ),

RK₂ =E_K (К₂ RK₁ ),

RK₃ =E_K (K₃ RK₂ ),

RK₄ =E_k (K₄ RK₃ ),

RK₅ =E_k (K₂ (1)RK₄ ),

RK₆ =E_K (К₂ (2)RK₅ ),

RK₇ =Е_К (К₃ (4)RK₆ ), RK₈ =E_k (K₄ (8)RK₇ ).(1.14)

Эта версия расписания ключей требует 8 расписаний ключей DES и 8 зашифрований DES на фиксированном ключе. Подключи нужно сгенерировать только один раз, если их впоследствии сохранить.

Заметим, что для всех версий расписания ключей 64-х битные величины RKi используются как ключи DES, поэтому биты проверки четности RKi не используются в i-ом цикле. Однако, все 64 бита RKi, как выхода шифрования на ключе К, используются при генерации следующего подключа.

Принципы разработки расписания ключей, во-первых, состоят в том, чтобы подключи зависели от наибольшего числа битов основного ключа, но не требовали при этом много работы, во-вторых, при вводе s основных ключей размером по 64 бит, любые s последовательных подключей должны иметь энтропию s · 56 бит, и, наконец, не должно быть очевидно зависимых и слабых ключей и не должно остаться свойство дополнительности. Заметим, что последние две проблемы присутствуют и в DES, и -все три - в тройном DES. Мы заметили, что если основные ключи размером по 64 бита каждый, может найтись пара ключей, генерирующих одинаковые множества подключей. Однако, число таких ключей, похоже, настолько невелико, что не представляет угрозы DEALy, применяемому для шифрования.

Смещения (i) введены для предотвращения появления слабых ключей. Если бы их не было, существовали бы ключи, для которых все подключи были равны. Например, для DEAL-128 ключи K1 = K2 = D_k (0) сгенерировали бы 6 подключей со значением 0. Смещения и шифрование на фиксированном ключе предотвращают появление слабых и зависимых ключей и свойства дополнительности.

Заметим, что если бит проверки четности используется в каждом байте основного ключа, действующие размеры предложенных ключей составляют 112, 168 и 224 бит соответственно.

Что можно сказать о стойкости DEAL в целом? Прежде всего, заметим[15], что для DEAL простая атака meet-in-the-middle (встретить по середине), аналогичная такой атаке на двойной DES, отыщет ключи за время порядка 2¹⁶⁸ зашифрований для шести, и 2²²⁴ зашифрований для восьми циклов DEAL соответственно, независимо от расписания ключей. Именно поэтому, предлагается в DEAL-256 производить по крайней мере 8 циклов зашифрования. Для DEAL-128 исчерпывающий поиск ключа займет время порядка 2¹¹² зашифрований.

Самая быстрая из известных атак по нахождению ключа на DEAL (с шестью циклами) - общая атака на 6-и цикловые Фейстелевы шифры, в приложении к DEAL, она требует порядка 2¹²¹ зашифрований DES, используя порядка 2⁷⁰ выбранных открытых текстов, для любого расписания ключей. В дальнейшем определим разность между двумя последовательностями бит, как побитное XOR.

В конце этого раздела подведем итог особенностям DEAL.

-DEAL имеет размер блока 128 бит и размер ключа 128, 192 или 256бит (действующий размер, соответственно, - 112, 168 или 224 бита).

- атака по подобранному шифр-тексту требует порядка 2⁶⁴ блоков шифр-текста.

- нет известных, вероятных атак.

- DEAL с шестью циклами имеет скорость, аналогичную скорости тройного DES.

- DEAL может использоваться в стандартных режимах работы.

- DEALможет быть реализован на имеющемся аппаратном и программном обеспечение DES.

- нет очевидно слабых ключей и устранено свойство дополнительности.

Наконец, позволим себе заметить, что ввиду довольно сложного расписания ключей, DEAL не практично использовать в случайных функциях.

Собственно результаты стойкости DEAL:

- Существуют эквивалентные ключи для DEAL-192 и DEAL-256.

Алгоритм нахождения требует около шести шифрований DES, чтобы найти набор из 256 эквивалентных ключей для DEAL-192, и восемь шифрований DES, чтобы найти 256 эквивалентных ключей для DEAL-256.

- Существуют эквивалентные ключи для DEAL-128 и алгоритм их нахождения, требующий около 2⁶⁴ вычислений для нахождения пары эквивалентных ключей.

- Атака математически-связанных ключей (related-keyattack) на DEAL-192 и DEAL-256, требующая три блока открытого текста, под 2³³ ключами с точным соответствием, 3*2⁴⁵ байт памяти и около 2¹³⁷ шифрований DEAL, чтобы найти последние два цикловых подключа для DEAL-192 и DEAL-256. (С большим количеством памяти это можно сделать быстрее).

- несколько возможных расширений этих атак. DEAL-192 может быть дешифрован до четырех циклов, а затем может быть применена атака Бихама (Bihams) на четырехцикловый цепной DES; DEAL-256 может быть дешифрован до шести циклов, а затем может быть применена атака на шестицикловый DEAL-192 подробнее эта операция описана [15].

Эти результаты интересны как для практики, так и для теории. Похоже, что DEAL будет иметь некоторое применение в будущем. DEAL кандидат на AES, но даже если он не станет финалистом, он почти наверняка будет использоваться. Как было указано на первой конференции по AES, широкое распространение железа под DES делает DEAL относительно легким для реализации во многих устройствах за очень низкую цену.

В реальном применении эквивалентные ключи DEAL имеют важное практическое следствие - они делают многие стандартные методы хэширования ненадежными.

Атака основанная на математически зависимых ключах вероятно менее применима, но все ещё может быть важна для некоторых приложений эти атаки снимают два последних цикла DEAL ценой примерно 2¹³⁷ шифрований DEAL, используя 3*2⁴⁵ байт памяти и требует все те же три блока открытого текста, зашифрованного 2³³ зависимыми ключами. Возможны компромиссы времени-памяти.

В настоящее время, имея 3*2⁶⁹ байт памяти, атака будет занимать 2¹¹³ вычислительных ресурсов, восстанавливая два последних подключа. После, можно реализовать атака Бихама (Bihams) на четырехцикловый цепной DES, которая требует ещё 2³³ блока открытого текста, зашифрованного только одним ключом, и 2⁸⁸ времени. Таким образом, вся атака займет приблизительно 2¹¹³ вычислительной работы, 3*2⁶⁹ байт памяти, все те же три блока открытого текста, зашифрованного 2³³ зависимыми ключами, ещё 2³² блока открытого текста, зашифрованного только одним ключом, которые должны быть выбраны ПОСЛЕ завершения первой атаки. По сравнению с лучшей из ранее известных атак, требующей 2¹¹⁹ вычислительной работы, 2⁶⁴ памяти и 2⁷⁰ выбранных открытых текстов.

На теоретическом уровне эти результаты показывают важный факт: Широко считается, что назначение ключей (keyshedule), которое использует сильные элементы криптографии будет практически неуязвимо к криптографическому анализу. Это утверждение, к сожалению, не верно. В DEAL используется сильный шифр в очевидно-разумном направлении, чтобы обрабатывать ключ. Однако, использованный метод оставляет уязвимость шифра к анализу зависимого ключа, также оставляет возможность эквивалентных ключей.

1.3 Crypton как перспективный алгоритм

Шифр Crypton представлен южнокорейской компанией FutureSystems, с конца 1980-х годов работающей на рынке сетевого обеспечения и защиты информации. Автор алгоритма Че Хун Лим [15],[16] признает, что конструкция его шифра во многом опирается на идеи шифра SQUARE бельгийских криптографов Дамена и Рэмена (также участвующих в конкурсе). Здесь нет традиционной для многих блочных шифров структуры Фейстела, оперирующей в каждом цикле шифрования половиной блока данных (например, как в DES или CAST). Основу данного шифра составляет другая стандартная конструкция - так называемая SP-сеть, т.е. повторяющаяся цикловая функция из замен-перестановок, ориентированная на распараллеленную нелинейную обработку всего блока данных. Помимо высокой скорости, к преимуществам такой конструкции относят и то, что она облегчает исследование стойкости шифра к методам дифференциального и линейного криптоанализа, являющимся на сегодня основными инструментами вскрытия блочных шифров.

Шифр Crypton, как и Square, эффективно реализуется на разнообразных платформах, и признано, что в корейском алгоритме присутствуют талантливые конструктивные идеи.

1.3.1 Алгоритм CRYPTON

Описание алгоритма было взято из книги автора шифра CRYPTON Че Хун Лим [16] В CRYPTON, каждый блок данных 128 бит представлен в форме массива 44 байта. Циклическое преобразование в CRYPTON состоит из четырех шагов: byte-wise substitutions(байт замена), column-wise bit permutation(колончастый способ перестановки битов), column-to-row transposition(перенос столбцов), и key addition(добавление ключа). Процесс кодирования состоит из4 раундов такихциклических преобразований. Процесс расшифровки может быть сделан идентичным процессу кодирования с различным ключевым списком. На рисунке 1.1 показана структура CRYPTON.

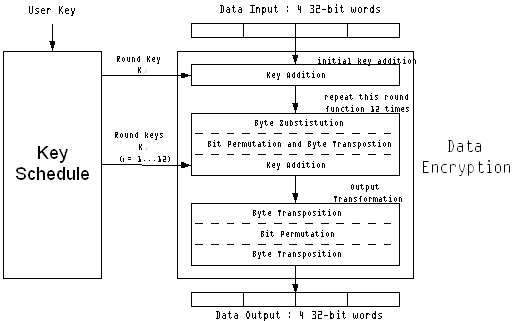
Рис.1.1 Структура CRYPTON.

Блочный шифр CRYPTON имеет следующие характеристики:

- 12-раундовый самозаменяемый шифр (с одинаковыми процессами для кодирования и расшифрования) с длиной блока 128 битов и длинной ключа до 256 битов.

- хорошая стойкость от существующих атак.

- эффективен и на программном и на аппаратном уровне: благодаря высокой степени паралельности и использованию очень простых логических операций ANDS/XORS, CRYPTON запускается очень быстро на большинстве платформ как в программном обеспечении так и в аппаратных средствах.

- Быстрое формирование ключей: шифрование со списоком ключей идет намного быстрее чем шифрование с одним блоком, так что это очень эффективно в приложениях, требующих частые замены ключей (например, в хеш-режиме).

1.3.2 Основные преобразования блока

1.3.2.1 Байтовая подстановка g

CRYPTON использует нелинейную замену байта, используя четыре 88 S-блока, S_i (0 i 3). Эти S-блоки получены из одного 88 S-блока при возведении в степень S (то есть, S = S^-1 ) и удовлетворяют обратные отношения S₂ =S₀ ^-1 и S3=S₁ ^-1 . Возведенный в степень S-блок S был, сформирован для более эффективной логической реализации.

Преобразование S-блока состоит из замен байт относительно массива 44 байт. Два различных преобразования используются альтернативно в последовательных раундах: в нечетных раундах и _e в нечетных раундах. Это показано на рисунке 1.2. Заметим, что эти четыре S-блока устроены так, что следующее закрепляются на любом 44 байте масива A:

g_o (g_e (A)) = g_e (g_o (A)) = A. (1.1)

Это свойство используется, чтобы получить идентичный процесс для кодирования и расшифровки.

A[0]	a₀₃	a₀₂	a₀₁	a₀₀	B[0]	S₃ (a₀₃ )	S₂ (a₀₂ )	S₁ (a₀₁ )	S₀ (a₀₀ )
A[1]	a₁₃	a₁₂	a₁₁	a₁₀	_o	B[1]	S₀ (a₁₃ )	S₃ (a₁₂ )	S₂ (a₁₁ )	S₁ (a₁₀ )
A[2]	a₂₃	a₂₂	a₂₁	a₂₀		B[2]	S₁ (a₂₃ )	S₀ (a₂₂ )	S₃ (a₂₁ )	S₂ (a₂₀ )
A[3]	a₃₃	a₃₂	a₃₁	a₃₀	B[3]	S₂ (a₃₃ )	S₁ (a₃₂ )	S₀ (a₃₁ )	S₃ (a₃₀ )
A[0]	a₀₃	a₀₂	a₀₁	a₀₀	B[0]	S₁ (a₀₃ )	S₀ (a₀₂ )	S₃ (a₀₁ )	S₂ (a₀₀ )
A[1]	a₁₃	a₁₂	a₁₁	a₁₀	_e	B[1]	S₂ (a₁₃ )	S₁ (a₁₂ )	S₀ (a₁₁ )	S₃ (a₁₀ )
A[2]	a₂₃	a₂₂	a₂₁	a₂₀		B[2]	S₃ (a₂₃ )	S₂ (a₂₂ )	S₁ (a₂₁ )	S₀ (a₂₀ )
A[3]	a₃₃	a₃₂	a₃₁	a₃₀	B[3]	S₀ (a₃₃ )	S₃ (a₃₂ )	S₂ (a₃₁ )	S₁ (a₃₀ )

Рис.1.2 Байтовая подстановка g

1.3.2.2 Битовая перестановка p и байтовое перемещение t

Как линейные преобразования, CRYPTON использует последовательную перестановку бита и перемещения байта. Бит-перестановка смешивает каждый столбец байта в массиве 44 байта и байт-перемещение перемещает результирующие столбцы байт в строки байт.

Сначала определяем четыре вектора маскировки (M3, M2, M1, M0) для извлечения бит, используемых в как:

M₀ = m₃ || m₂ || m₁ || m₀ = 0x3fcff3fc,

M₁ = m₀ || m₃ || m₂ || m₁ = 0xfc3fcff3,

M₂ = m₁ || m₀ || m₃ || m₂ = 0xf3fc3fcf,

M₃ = m₂ || m₁ || m₀ || m₃ = 0xcff3fc3f, (1.3)

Где m0 = 0xfc, m1 = 0xf3, m2 = 0xcf, m3 = 0x3f. Чтобы сделать процес шифрования и расшифрования идентичными, используются два немного различных варианта перестановки; в нечетных раундах и _e в четных раундах. Они определены следующим образом:

- байтовое перемещение _o для нечетных раундов: B = _o (A) определяется как:

B[0] - (A[3] M₃ ) (A[2] M₂ ) (A[1] M₁ ) (A[0] M₀ ),

B[1] - (A[3] M₀ ) (A[2] M₃ ) (A[1] M₂ ) (A[0] M₁ ),

B[2] - (A[3] M₁ ) (A[2] M₀ ) (A[1] M₃ ) (A[0] M₂ ),

B[3] - (A[3] M₂ ) (A[2] M₁ ) (A[1] M₀ ) (A[0] M₃ ). (1.4)

- Битовая перестановка _e для четных раундов: B=_e (A) определяется как:

B[0] - (A[3] M₁ ) (A[2] M₀ ) (A[1] M₃ ) (A[0] M₂ ),

B[1] - (A[3] M₂ ) (A[2] M₁ ) (A[1] M₀ ) (A[0] M₃ ),

B[2] - (A[3] M₃ ) (A[2] M₂ ) (A[1] M₁ ) (A[0] M₀ ),

B[3] - (A[3] M₀ ) (A[2] M₃ ) (A[1] M₂ ) (A[0] M₁ ). (1.5)

Битовая перестановка просто перестраивает массив 44 байта, перемещая байт из (i, j)-ой позиции в (j, i)-ую позицию (См. Рисунок 1.3для B=

A[0]	a₀₃	a₀₂	a₀₁	a₀₀	B[0]	a₃₀	a₂₀	a₁₀	a₀₀
A[1]	a₁₃	a₁₂	a₁₁	a₁₀		B[1]	a₃₁	a₂₂	a₁₁	a₀₁
A[2]	a₂₃	a₂₂	a₂₁	a₂₀		B[2]	a₃₂	a₂₂	a₁₂	a₀₂
A[3]	a₃₃	a₃₂	a₃₁	a₃₀	B[3]	a₃₃	a₂₃	a₁₃	a₀₃

Рис. 1.3 байтовое перемещение t

1.3.2.3 Добавление ключа s

K = (K[3], K[2], K[1], K[0])^t , B = (A) определяетсякакB[i] = A[i] K[i], где i = 0, 1, 2, 3.

1.3.2.4 Циклическое преобразование r

Один цикл CRYPTON состоит из применения в последовательности преобразование S-блока, байт-перестановки, байт-перемещения и дополнение ключа. То есть цикл кодирования функций, используемых для нечетного и четного цикла, определены (для циклического ключа K)

r_oK = s_K t p_o g_o

для r = 1, 3, ... etc.,(1.6)

r_eK = s_K t p_e g_e for r = 2, 4, ... etc. (1.7)

1.3.3 Шифрование и расшифрование

Преобразование кодирования E_K r-циклов CRYPTON под ключом K состоит из начального добавления ключа и r/2 повторений и _e затем заключительное преобразование вывода. Кодирование и расшифровка могут быть выполнены тем же самым кодом, если применяются различные циклические ключи.

1.3.4 Формирование ключей

R-цикл CRYPTON требует общего количества 4 (r + 1) цикловых ключей 32-битной длины. Эти циклические ключи произведены от ключа пользователя 8k (k = 0,1, ..., 32) бит в два этапа: сначала нелинейное преобразование ключа пользователя в 8 расширенных ключей и затем генерируется необходимое количество циклических ключей от этих расширенных ключей, использующих простые операции.

1.4 Основные виды криптоанализа БСШ и определения надежности СЗИ

Криптология довольно четко делится на две части: криптографию (шифрование) и криптоанализ. Криптограф пытается найти методы обеспечения секретности и(или) аутентичности (подлинности) сообщений [18]. Криптоаналитик пытается выполнить обратную задачу, раскрывая шифр или подделывая кодированные сигналы таким образом, чтобы они были приняты как подлинные. Исходное сообщение, которому криптограф применяет свое искусство, называется открытым текстом, а результат его работы — шифрованным текстом сообщения — шифртекстом, или криптограммой. Для управления процессом шифрования криптограф всегда использует секретный ключ. Часто (но не всегда) он передает этот секретный ключ каким-либо надежным способом (например, в дипломате, пристегнутом наручниками к руке курьера) человеку (или машине), которому он собирается позднее послать криптограмму, составленную с использованием этого ключа.

Почти общепринятое допущение в криптографии состоит в том, что криптоаналитик противника имеет полный текст криптограммы. Кроме того, криптограф почти всегда руководствуется правилом, впервые сформулированным голландцем Керкхоффом: стойкость шифра должна определяться только секретностью ключа. Иными словами, правило Керкхоффа состоит в том, что весь механизм шифрования, кроме значени секретного ключа, известен криптоаналитику противника. Если криптограф принимает только эти два допущения, то он разрабатывает систему, стойкую при анализе на основе только шифрованного текста. Если к тому же криптограф допускает, что криптоаналитик противника сможет достать несколько отрывков открытого текста и соответствующего ему шифрованного текста, образованного с использованием секретного ключа, то разрабатывается система, стойка при анализе на основе открытого текста. Криптограф может даже допустить, что криптоаналитик противника способен ввести свой открытый текст и получить правильную криптограмму, образованную с использованием секретного ключа (анализ на основе выбранного открытого текста), или предположить, что криптоаналитик противника может подставить фиктивные криптограммы и получить текст, в который они превращаются при расшифровании (анализ на основе выбранного шифртекста), или допустить обе эти возможности (анализ на основе выбранного текста). Разработчики большинства современных шифров обеспечивают их стойкость к анализу на основе выбранного открытого текста даже в том случае, когда предполагается, что криптоаналитик противника сможет прибегнуть к анализу на основе шифртекста.

Системы и средства защиты информации (СЗИ) отличаются от обычных систем и средств тем, что для них не существует простых и однозначных тестов, которые позволяют убедиться в том, что информация надежно защищена[19]. Кроме того, эффективность СЗИ и просто их наличие никак не связываются на работоспособности основной системы. Поэтому задача эффективности СЗИ не может быть решена обычным тестированием. Например, для проверки работоспособности системы связи достаточно провести ее испытания. Однако успешное завершение этих испытаний не позволяет сделать вывод о том, что встроенная в нее подсистема защиты информации тоже работоспособна.

Задача определения эффективности СЗИ (особенно, если используются криптографические методы защиты), зачастую более трудоемкая, чем разработка СЗИ, требует наличия специальных знаний и, как правило, более высокой квалификации, чем задача разработки. Часто анализ нового шифра является новой научной, а не инженерной задачей.

Эти обстоятельства приводят к тому, что на рынке появляется множество средств криптографической защиты информации, про которые никто не может сказать ничего определенного. При этом разработчики держат криптоалгоритм (как показывает практика, часто нестойкий) в секрете. Однако задача точного определения данного криптоалгоритма не может быть гарантированно сложной хотя бы потому, что он известен разработчикам. Кроме того, если нарушитель нашел способ преодоления защиты, то не в его интересах об этом заявлять. В результате, пользователи таких СЗИ попадают в зависимость как минимум от разработчика. Поэтому обществу должно быть выгодно открытое обсуждение безопасности СЗИ массового применения, а сокрытие разработчиками криптоалгоритма должно быть недопустимым.

Криптосхемой или криптоалгоритмом будем называть собственно алгоритм шифрования.

Принято различать криптоалгоритмы по степени доказуемости их безопасности [20]. Существуют безусловно стойкие, доказуемо стойкие и предположительно стойкие криптоалгоритмы. Безопасность безусловно стойких криптоалгоритмов основана на доказанных теоремах о невозможности раскрытия ключа. Примером безусловно стойкого криптоалгоритма является система с разовым использованием ключей (шифр Вернама) или система квантовой криптографии, основанная на квантовомеханическом принципе неопределенности. Стойкость доказуемо стойких криптоалгоритмов определяется сложностью решени хорошо известной математической задачи, которую пытались решить многие математики и которая является общепризнанно сложной. Примером могут служить системы Диффи-Хеллмана или Ривеста-Шамира- Адельмана, основанные на сложностях соответственно дискретного логарифмирования и разложения целого числа на множители. Предположительно стойкие криптоалгоритмы основаны на сложности решения частной математической задачи, которая не сводится к хорошо известным задачам и которую пытались решить один или несколько человек. Примерами могут криптоалгоритмы ГОСТ 28147-89, DES, FEAL.

К сожалению безусловно стойкие криптосистемы неудобны на практике (системы с разовым использованием ключа требуют большой защищенной памяти для хранения ключей, системы квантовой криптографии требуют волоконно-оптических каналов связи и являются дорогими, кроме того, доказательство их безопасности уходит из области математики в область физики).

Достоинством доказуемо стойких алгоритмов являетс хорошая изученность задач, положенных в их основу. Недостатком их являетс невозможность оперативной доработки криптоалгоритмов в случае появлени такой необходимости, то есть жесткость этих криптоалгоритмов. Повышение стойкости может быть достигнуто увеличением размера математической задачи или ее заменой, что, как правило, влечет цепь изменений не только в шифрованной, но и смежной аппаратуре.

Предположительно стойкие криптоалгоритмы характеризуютс сравнительно малой изученностью математической задачи, но зато обладают большой гибкостью, что позволяет не отказываться от алгоритмов, в которых обнаружены слабые места, а проводить их доработку.

Задача обеспечения защищенной связи включает в себя целый комплекс проблем. Это задача обеспечения секретности и имитозащиты, опознавания (аутентификации) и задача управления ключами, включая их выработку, распределение и доставку пользователям, а также их оперативную замену в случае необходимости.

Общая схема организации защищенной связи приведена на рисунке 1.11 [21].

Этой же схемой описывается и абонентское шифрование, когда пользователь шифрует информацию, хранимую в памяти ЭВМ. В последнем случае источник сообщений и получатель отождествляется, а канал связи может иметь произвольные задержки.

Источник сообщений вырабатывает произвольную информацию (открытые тексты) с каким-то распределением вероятностей. Шифратор шифрует это сообщение на конфиденциальном (известном только отправителю и получателю) ключе Z и переводит открытый текст в шифрованный текст или шифрограмму (криптограмму, шифртекст).

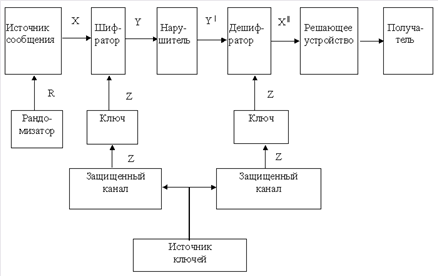
Рис. 1.11 Общая схема организации защищенной связи

Ключи вырабатываются источником ключей и по безопасным каналам рассылаются абонентом сети связи. Дешифратор раскрывает принятую шифрограмму и передает получателю.

В схему на рисунке 1.11. включены еще рандомизатор и решающее устройство. Рандомизатор делает все шифрограммы непохожими друг на друга, даже если входные сообщения одинаковы. Цель этого будет разъяснена ниже. Решающее устройство принимает решение о том, является ли принятое сообщение подлинным, то есть выполняет функцию имитозащиты.

Операции шифрования и расшифрования можно описать так:

Y = E(X), X = D(Y)(1.16)

Для взаимной однозначности необходимо, чтобы DE было единичным преобразованием. В этом разделе будет предполагать наличие у отправителя и получателя общего секретного ключа Z. (На самом деле ключи у них не обязательно одинаковые, но знание одного ключа, например шифрования, позволяет легко вычислить другой. Поэтому рассматриваемые криптоалгоритмы иногда называют симметричными, или одноключевыми. Соответственно, и криптография, занимающаяся изучением таких алгоритмов, называется одноключевой). Данная схема применяется в том случае, если абоненты сети доверяют друг другу.

Ниже показано, как с помощью одноключевой криптографии решаются вопросы имитозащиты и опознавания (секретность обеспечивается очевидным образом). Подлинность и целостность сообщения обеспечиваются его криптографическим преобразованием, выполняемым с помощью секретного ключа. Например, если отправитель передаст сразу и открытый (не требующий засекречивания), и зашифрованный тексты, то это позволит получателю, знающему ключ, утверждать, что текст при передаче по каналу связи не был изменен, если результат расшифрования шифрограммы совпадает с открытым текстом. Действительно, случайное совпадение соответствующих друг другу открытого текста и шифрограммы — практически невозможное событие. Эту пару мог составить лишь отправитель, знающий секретный ключ. Отсюда следует и подлинность сообщения (отправитель отождествляется с владельцем ключа). В действительности нет необходимости передавать всю шифрограмму, достаточно передать лишь ее часть, называемую имитовставкой, которая должна зависеть от всего открытого текста. Тогда получатель может на основании полученного текста и ключа вычислить свою имитовставку и проверить ее соответствие полученной.

Для опознавания пользователя используется следующий диалог. Проверяющий вырабатывает случайный текст и посылает опознаваемому для шифрования. Опознаваемый шифрует этот текст и возвращает проверяющему. Тот проверяет соответствие шифрограммы тексту. Правильный ответ может составить только владелец секретного ключа, который отождествляется с законным пользователем. Очевидно, что прослушивающий диалог нарушитель не сможет правильно зашифровать новый текст и назваться пользователем. (Исключением является аналогия известного жульничества, примененного при игре в шахматы по почте, когда нарушитель просто транслирует ответы и запросы подлинным проверяющему и проверяемому, ведя диалог одновременно с каждым из них). Принципиальное отличие данной системы от опознавания по паролю, где подслушивание позволяет узнать секретный пароль и в дальнейшем воспользоваться этим, заключается в том, что здесь по каналу связи секретная информация не передается. Ясно, что и стойкость шифрования, и имитостойкость, и стойкость опознавания могут быть обеспечены, если положенное в основу криптопреобразование является стойким в смысле раскрытия ключа.

Уровень стойкости зависит от возможностей криптоаналитика и от пользователя. Так, различают криптоанализ на основе только шифрованного текста, когда криптоаналитик располагает только набором шифрограмм и не знает открытых текстов, и криптоанализ на основе открытого текста, когда криптоаналитик знает и открытие, и соответствующие шифрованные тексты. Поскольку криптоалгоритм обычно должен быть достаточно универсальным, естественным представляется требование, чтобы стойкость ключа не зависела от распределени вероятностей источника сообщений. В общем случае источник сообщений может вырабатывать удобные для нарушителя сообщения, которые могут стать ему известными. В этом случае говорят о криптоанализе на основе специально выбранных открытых текстов. Очевидно, что стойкость ключа по отношению к анализу на основе выбранных текстов не может превышать стойкости по отношению к анализу на основе открытых текстов, а она, в свою очередь, не может превышать стойкости по отношению к анализу на основе шифрованных текстов. Иногда разработчиком СЗИ допускается даже, что враждебный криптоаналитик может иметь доступ к криптосистеме, то есть быть своим.

Обычно криптоалгоритмы разрабатывают так, чтобы они были стойкими по отношению к криптоанализу на основе специально выбранных открытых текстов.

Понятие наилучшего алгоритма раскрытия ключа в определении стойкости неконструктивно и допускает субъективное толкование (для кого- то из разработчиков наилучшим алгоритмом может быть простой перебор ключей). По-видимому, ни для одного из используемых криптоалгоритмов не определен наилучший алгоритм раскрытия ключа, то есть задача нахождени наилучшего алгоритма является чрезвычайно сложной. Поэтому на практике для оценки стойкости пользуются наилучшим известным или найденным в ходе исследований алгоритмом раскрытия. Таким образом, на практике никто не может помешать способному криптоаналитику снизить оценку стойкости, придумав новый, более эффективный метод анализа.

Создание новых эффективных методов раскрытия ключа или иного метода ослабления криптоалгоритма может давать осведомленным лицам большие возможности по нанесению ущерба пользователям, применяющим данный криптоалгоритм. Публикация или замалчивание этих сведений определяются степенью открытости общества. Рядовой пользователь системы бессилен помешать нарушителю в раскрытии его ключей.

Из изложенного следует, что понятие наилучшего известного алгоритма неабсолютно: завтра может появиться новый более эффективный алгоритм раскрытия, который приведет к недопустимому снижению стойкости криптоалгоритма. С развитием математики и средств вычислительной техники стойкость криптоалгоритма может только уменьшаться. Для уменьшения возможного ущерба, вызванного несвоевременной заменой криптоалгоритма, потерявшего свою стойкость, желательна периодическая перепроверка стойкости криптоалгоритма. Для снижения вероятности непредсказуемого обвала вновь разработанного криптоалгоритма необходимо проведение криптографических исследований.

Из рассмотренного выше следует, что понятие стойкости криптосистемы многогранно. Стойкость зависит не только от разработчика, но и от особенностей использования данного криптоалгоритма в системе управлении или связи, от физической реализации криптоалгоритма, а также от будущих успехов математики и вычислительной техники. Ведь криптосистема может эксплуатировать много лет, а необходимость сохранять в секрете в течение длительного времени переданную ранее по открытым каналам связи информацию может сделать необходимым прогнозировать развитие науки и техники на десятилетия.

Последние десятилетие характеризуется резким увеличением числа открытых работ по всем вопросам криптологии, а криптоанализ становится одной из наиболее активно развивающихся областей исследований. Многие криптосистемы, стойкость которых не вызывала особых сомнений, оказались успешно раскрытыми. При этом разработан большой арсенал математических методов, представляющих прямой интерес для криптоаналитика.

В начале 1970-х гг. была известна только классическая одноключевая криптография, но число открытых работ по этой тематике было весьма скромным. Отсутствие интереса к ней можно объяснить целым рядом причин. Во-первых, острой потребности в криптосистемах коммерческого назначения, по-видимому, еще не ощущалось. Во-вторых, большой объем закрытых исследований по криптографии обескураживал многих ученых, которым, естественно, хотелось получить новые результаты. И наконец, может быть, самый важный фактор заключается в том, что криптоанализ как научная дисциплина фактически по-прежнему представлял собой большой набор разрозненных трюков, не объединенных стройной математической концепцией.

В 1970-х гг. ситуация радикально изменилась. Во-первых, с развитием сетей связи и повсеместным вторжением ЭВМ необходимость в криптографической защите данных стала осознаваться все более широкими слоями общества. Во-вторых, изобретение Диффи и Хелманном криптографии с открытым ключом создало благоприятную почву для удовлетворения коммерческих потребностей в секретности, устранив такой существенный недостаток классической криптографии, как сложность распространения ключей. По существу, это изобретение гальванизировало научное сообщество, открыв качественно новую неисследованную область, которая к тому же обещала возможность широкого внедрения новых результатов быстро развивающейся теории вычислительной сложности для разработки конкретных систем с простым математическим описанием. Ожидалось, что стойкость таких систем будет надежно опираться на неразрешимость в реальном времени многих хорошо известных задач и что, может быть, со временем удастся доказать принципиальную нераскрываемость некоторых криптосистем.

Но надежды на достижение доказуемой стойкости посредством сведения задач криптографии к хорошо известным математическим задачам не оправдалась, а, скорее, наоборот. Именно то обстоятельство, что любую задачу отыскани способа раскрытия некоторой конкретной криптосистемы можно переформулировать как привлекательную математическую задачу, при решении которой удается использовать многие методы той же теории сложности, теории чисел и алгебры, привело к раскрытию многих криптосистем. На сегодняшний день классическая лента однократного использования остается единственной, безусловно, стойкой системой шифрования.

Идеальное доказательство стойкости некоторой криптосистемы с открытым ключом могло бы состоять в доказательстве того факта, что любой алгоритм раскрытия этой системы, обладающий не пренебрежимо малой вероятностью ее раскрытия, связан с неприемлемо большим объемом вычислений. И хотя ни одна из известных систем с открытым ключом не удовлетворяет этому сильному критерию стойкости, ситуацию не следует рассматривать как абсолютно безнадежную. Было разработано много систем, в отношении которых доказано, что их стойкость эквивалентна сложности решения некоторых важных задач, которые почти всеми рассматриваются как крайне сложные, таких, например, как известная задача разложения целых чисел. (Многие из раскрытых криптосистем были получены в результате ослабления этих предположительно стойких систем с целью достижения большого быстродействия.) Кроме того, результаты широких исследований, проводившихся в течение последних десяти лет как в самой криптографии, так и в общей теории вычислительной сложности, позволяют современному криптоаналитику гораздо глубже понять, что же делает его системы нестойкими.

Проведение криптоанализа для давно существующих и недавно появившихся криптоалгоритмов очень актуально, так как вовремя можно сказать, что данный криптоалгоритм нестоек, и усовершенствовать его или заменить новым. Для того, чтобы выявлять нестойкие криптоалгоритмы необходимо все время совершенствовать уже известные методы криптоанализа и находить новые.

Направление криптоанализа могут быть различными, в соответствии с направлениями криптографии: это раскрытие ключа, навязывание ложной информации за счет нахождения слабостей в криптоалгоритме или протоколе, возможность бесконечного чтения зашифрованной информации и т.п.

Криптоалгоритм, как правило, должен быть стойким по отношению к криптоанализу на основе выбранных открытых текстов. Первое требование по существу означает, что рассекречивание некоторой информации, передававшейся по каналу связи в зашифрованном виде, не должно приводить к рассекречиванию другой информации, зашифрованной на этом ключе. Второе требование учитывает особенности эксплуатации аппаратуры и допускает некоторые вольности со стороны оператора или лиц, имеющих доступ к формированию засекреченной информации.

Криптоанализ может базироваться на использовании как общих математических результатов (например методов разложения больших чисел для раскрытия криптосистемы RSA), так и частных результатов, полученных для конкретного криптоалгоритма. Как правило, алгоритмы криптоанализа являются вероятностными.

Дифференциальный метод криптоанализа [21] (ДКА) был предложен Э.Бихамом и А.Шамиром в 1990 г. Дифференциальный криптоанализ - это попытка вскрытия секретного ключа блочных шифров, которые основаны на повторном применении криптографически слабой цифровой операции шифрования r раз. При анализе предполагается, что на каждом цикле используется свой подключ шифрования. ДКА может использовать как выбранные, так и известные открытые тексты .

Отличительной чертой дифференциального анализа является то, что он практически не использует алгебраические свойства шифра (линейность, аффинность, транзитивность, замкнутость и т.п.), а основан лишь на неравномерности распределения вероятности дифференциалов.

В открытой печати линейный метод криптоанализа впервые был предложен японским математиком Мацуи. Метод предполагает, что криптоаналитик знает открытые и соответствующие зашифрованные тексты.

Обычно при шифровании используется сложение по модулю 2 текста с ключом и операции рассеивания и перемешивания. Задача криптоаналитика - найти наилучшую линейную аппроксимацию (после всех циклов шифрования)

Для раскрытия ключа шифра DES этим методом необходимо 247 пар известных открытых и зашифрованных текстов.

1.5 Выводы по разделу

Исходя из выше изложенного материала можно сделать вывод, что БСШ Crypton является эффективным и на программном и на аппаратном уровне: благодаря высокой степени паралельности и использованию очень простых логических операций ANDS/XORS, CRYPTON работает очень быстро на большинстве платформ, как в программном обеспечении, так и в аппаратных средствах. Анализ безопасности БСШ Crypton показывает, что 12-раундовый самозаменяемый шифр (с одинаковыми процессами для кодирования и расшифрования) с длиной блока 128 битов и длинной ключа до 128 битов обладает хорошей стойкостью к существующим атакам. Интегральная атака на 4-х раундовый БСШ Crypton является намного эффективнее, чем полный перебор по всему ключевому пространству.

Поэтому реализация интегрального алгоритма атаки на БСШ Cryptonбудет наиболее актуальной задачей.

2. ОСОБЕННОСТИ РЕАЛИЗАЦИИ ИНТЕГРАЛЬНОЙ АТАКИ НА ШИФР CRYPTON

2.1 Интегральные свойства БСШ Crypton

Crypton представляет собой блочный шифр. Длина ключа и длина блока 128 бит. Описание алгоритма атаки взято из [22].

Четыре преобразования работают с промежуточным результатом, называемым Состоянием (State). Состояние можно представить в виде прямоугольного массива из 16 байт , где . Обозначим – столбец из четырех байт. Аналогично представлен ключ шифрования , где . Обозначим .

В шифре определено поле Галуа GF(2⁸ ), элементами которого являются байты. Байты рассматриваются как многочлены над Z₂ :

где i-й бит байта (0 или 1).

Операция сложения . При сложении байт соответствующие им многочлены складываются над Z₂ (1+1=0).

Операция умножения. При умножении байт соответствующие им многочлены перемножаются над Z₂ и результирующий многочлен берется по модулю простого многочлена

В процессе работы алгоритма ключ расширяется (Key Schedule, Key Expansion). Первые 4 столбца (по 4 байта) массива являются исходным ключом (). Каждый последующий r-й набор из 4 столбцов вычисляется из предыдущего набора и используется для r-ого раунда, обозначим его . Раунд состоит из четырех различных элементарных преобразований, которые преобразуют состояние в состояние :

1. Замена байт – BS (Byte Substitution): применение перестановки S (также известной как S-блок, Sbox) ко всем байтам состояния независимо. для .

2. Сдвиг строк – SR (Shift Rows): циклический сдвиг байт по правилу .

3. Замешивание столбцов – MC (Mix Columns): каждый столбец состояния изменяется линейным преобразованием . Преобразование можно представить, как умножение столбца на матрицу слева:

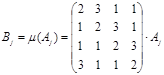
Операция обратима: .

4. Добавление раундового ключа – KA (Key Addition): к текущему состоянию прибавляется раундовый ключ .

Финальный раунд не содержит операции MC. Составим 2 формулы, связывающие состояния A^r-1 и A^r :

(1)

(2)

2.2 Алгоритм реализации интегральной атаки на БСШ Crypton

В данном разделе описана специфичная для шифра Crypton интегральная атака [22]. Представлено математическое обоснование базовой атаки на 4 раунда.

Интегральная атака основана на возможности свободного подбора атакующим некоторого набора открытых текстов для последующего их зашифрования. Эта атака для 4-раундового шифра Crypton (стандарт Crypton включает в себя 12 раундов) эффективнее, чем полный перебор по всему ключевому пространству.

Введем определения.

-набор – набор из 256 входных блоков (массивов State), каждый из которых имеет байты (назовем их активными), значения которых различны для всех 256 блоков. Остальные байты (пассивные) остаются одинаковыми для всех 256 блоков из -набора. Т.е. : , если байт с индексом активный и иначе.

^k – -набор c k активными байтами.

P_r – множество состояний в конце раунда r.

Возьмем -набор и проследим его изменение в течении нескольких раундов. После элементарных преобразований BS и KA блоки -набора дадут в результате другой -набор с активными байтами в тех же позициях, что и у исходного. Преобразование SR сместит эти байты соответственно заданным в ней смещениям. После преобразования MC -набор в общем случае необязательно останется -набором (т. е. результат операции может перестать удовлетворять определению -набора). Но поскольку каждый байт результата MC является линейной комбинацией (с обратимыми коэффициентами) четырех входных байт того же столбца , то столбец с единственным активным байтом на входе даст в результате на выходе столбец со всеми четырьмя активными байтами.

Рассмотрим шифрование ¹ -набора, во всех блоках которого активен только один байт. Т.е. значение этого байта различно во всех 256 блоках, а остальные байты одинаковы. Проследим эволюцию этого байта на протяжении трех раундов. В первом раунде преобразование MC преобразует один активный байт в столбец из 4 активных байт, т.е. P₁ является ⁴ . Во втором раунде эти 4 байта разойдутся по 4 различным столбцам в результате преобразования SR, P₂ является ¹⁶ . Преобразование MC следующего, третьего раунда преобразует эти байты в 4 столбца, содержащие активные байты. Этот набор все еще остается -набором до того момента, когда он поступает на вход MC третьего раунда.

Основное свойство -набора – поразрядная сумма по модулю 2 () всех байтов, находящихся на одних и тех же местах, по всему набору равна нулю, т.е. . Действительно, поразрядная сумма неактивных (с одинаковыми значениями) байт равна нулю по определению операции (т.к. ), а активные байты, пробегая все 256 значений, также при поразрядном суммировании дадут нуль.

Рассмотрим теперь результат преобразования MC в третьем раунде байтов входного массива данных A в байты выходного массива данных B. Покажем, что и в этом случае поразрядная сумма всех блоков выходного набора будет равна нулю, то есть:

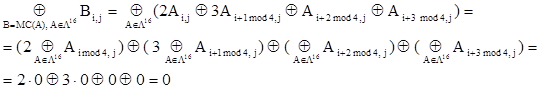
Таким образом, P₃ является ¹⁶ , т.е. все данные на входе четвертого раунда сбалансированы (их полная сумма равна нулю). Этот баланс в общем случае нарушается последующим преобразованием BS. Ключ K^r также можно однозначно задать в L-представлении, которое строится следующим образом:

Зная L^r можно вычислить K^r , и обратно. Для проведения атаки потребуется множество Q₄ состоящее из 256 состояний: . Множество Q₄ можно получить из выходных данных шифра P₄ применением 2 обратных преобразований SR^-1 и MC^-1 к каждому состоянию.

Схема базовой интегральной атаки на 4-раундовый Crypton.

Для всех

Для

Если , то

В этой схеме мы инвертируем 4-ый раунд шаг за шагом, чтобы получить сбалансированные байты P₃ . При сумма будет сбалансированной.

Если предполагаемое значение байта ключа было верно, то оно будет включено в возможные варианты на место . Большая часть неверных значений байта будет отсеяно. За счет того, что поиск может производиться отдельно (параллельно) для каждого байта ключа, скорость подбора всего значения раундового ключа весьма велика. Далее по значению можно найти , а потом и – исходный ключ [22].

2.3 Описание программной реализации

Разработанный в рамках дипломной работы программный продукт представляет собой реализацию шифрования и расшифрования данных с использованием алгоритма Cryptonи реализацию интегральной атаки. Системные требования - компьютер на базе IntelPentium и выше, ОС - Windows 95 + IE 4.0 и выше.

Программный продукт выполняет следующие операции:

- зашифрование входных данных в криптограму;

- расшифрование криптограммы;

- нахождение 128 – битного ключа.

Операция зашифрования выполняется следующим образом:

1. Запускаем файл ENCRDECR.EXE получаем на экране Рис.2.1

2. Нажатием кнопки 0 выбираем функцию зашифрования;

3. Указываем путь к файлу который необходимо зашифровать и путь где разместить криптограму Рис. 2.2

Рисунок 2.1 Начало работы программы

Рисунок 2.2 Указание пути к файлу

4. По указаному путимы получим криптограму.

Операция расшифрования выполняется следующим образом:

1. Запускаем файл ENCRDECR.EXE получаем на экране Рис.2.1

2. Нажатием кнопки 1 выбираем функцию расшифрования;

3. Указываем путь к криптограме и путь где разместить расшифрованный файл Рис. 2.3

Рисунок 2.3 Операция расшифрования

5. По указаному пути мы получим исходные данные.

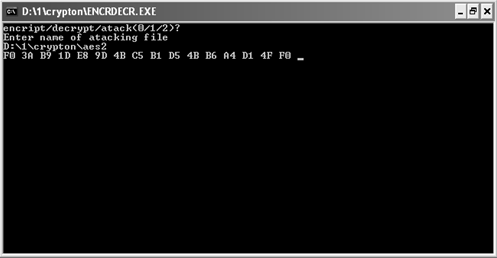
Операция нахождения ключа выполняется следующим образом:

1. Запускаем файл ENCRDECR.EXE получаем на экране Рис.2.1

2. Нажатием кнопки 2 выбираем функцию атаки;

3. Указываем путь к криптограме Рис. 2.4

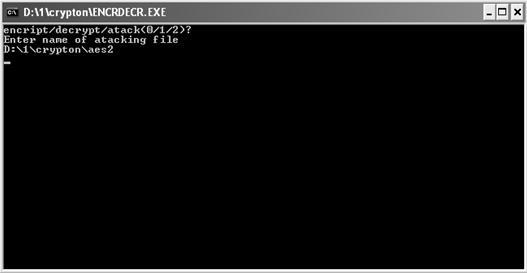
Рисунок 2.4 Операция нахождения ключа.

В результате получим наш ключ Рис.2.5

3. БЕЗОПАСНОСТЬ ЖИЗНЕДЕЯТЕЛЬНОСТИ

3.1 Анализ условий труда

Дипломный проект выполнялся в помещении научно - исследовательской лаборатории (НИЛ). При разработке применялись ПЭВМ. В дальнейшем при разработке вопросов БЖД будем использовать источники и нормативные документы, регулирующие вопросы БЖД при эксплуатации ПЭВМ [23, 12, 16].

Исследовательские работы выполнялись в помещении НИЛ,размеры которой составляют 4х6х3 м (площадь 24м² ). В помещении имеется 1 окно, площадью 6 м² . Рабочих мест 2 (2 программиста). Каждое рабочее место оборудовано ПЭВМ.

Помещение соответствует требованиям ДНАОП 0.00-1.31-99 - на одного работающего приходится 12 м² площади и, 36 м³ объема при норме 6 м² и 20 м³ соответственно.

Рассматривая НИЛ как систему Человек-Машина-Среда (Ч-М-С), можно выделить 2 подсистемы рабочее место, в состав каждой из которых входят элементы человек (работник), машина (ПЭВМ). Элемент среда (производственная среда в помещении НИЛ) является общим для подсистем рабочее место.

Элемент человек разделим на следующие функциональные части:

Ч1 – человек, выполняющий целенаправленные функции;

Ч2 – человек, рассматриваемый с точки зрения его влияния на среду за счет тепло-, влаговыделения и др.;

Ч3 – человек, рассматриваемый с точки зрения его психофизиологического состояния;

ПТ – предмет труда (проектирование программного продукта).

Элемент машина разделим на следующие части:

М1 – выполняет основную техническую функцию (программный продукт);

М2 – функции аварийной защиты (изоляция, предохранители);

М3 – управление окружающей средой (тепло, шум, электромагнитное излучение) (рисунок 1).

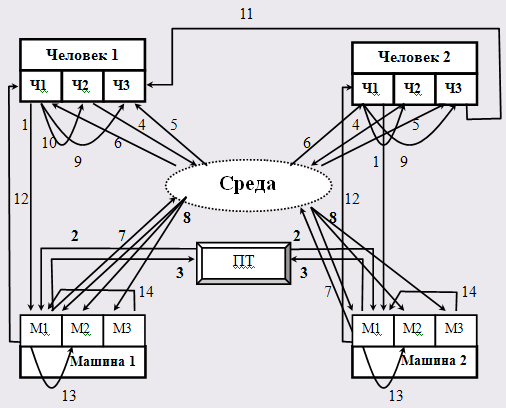
Рисунок 1. Система Человек-Машина-Среда для НИЛ

На рис. 1. приведены обозначения:

1 - (Ч1-М1) воздействие человека на управление машиной и ее настройки (программирование);

2 - (ПТ-М1) информация о состоянии предмета труда, управляемая машиной (исходные данные программы);

3 - (М1-ПТ) воздействие машины на предмет труда (компиляция программного кода);

4 - (Ч2-С) влияние человека на среду (теплообмен, шум) ;

5 - (С-Ч3) влияние среды на психофизиологическое состояние человека (утомление, перенапряженность анализаторов);

6 - (С-Ч1) влияние среды на качество работы человека (физическая и умственная активность);

7 - (М1-С) влияние машины на состояние среды (Эл.магн. излучение, тепло);

8 - (С-М1, С-М2, С-М3) влияние среды на качество работы машины (повышение температуры деталей компьютера);

9 - (Ч1-Ч3) связь выполняемой работы с психофизиологическим состоянием организма (утомление, умственная перенапряженность);

10 - (Ч1-Ч2) влияние характера труда на интенсивность обмена веществ ;

11 - (Ч3-Ч3) взаимодействие людей между собой ;

12 - (М1-Ч1) информация о состоянии машины, обрабатываемая человеком (программный код, изображенный на мониторе);

13 - (М1-М2) информационная связь между компьютером и защитной функцией;

14 - (М3-М1) аварийное управляющее воздействие.

Возникающие нецелевые (не связанные с выполнением работ) связи между элементами системы приводят к появлению опасных и вредных производственных факторов (ОВПФ). В таблице 1. перечислены, согласно [24]и ГОСТ 12.0.003-74 возможные ОВПФ с указанием их источника и последствий воздействия на человека.Помещение относится к классу помещений без повышенной опасности, поскольку нет признаков, свойственных особо опасным помещениям и помещениям с повышенной опасностью.Можно выделить следующие ОВПФ в помещении НИЛ.

Физические:

- повышенный уровень шума на рабочем месте;

- отсутствие или недостаток естественного света;

- недостаточная освещенность рабочей зоны;

- повышенная или пониженная температура воздуха рабочей зоны;

- повышенная или пониженная влажность воздуха рабочей зоны;

- повышенное значение напряжения в электрической цепи;

- повышенная напряженность электрического и магнитного поля;

- повышенный уровень ионизирующего излучения

Психофизиологические

- статические перегрузки;

- умственное перенапряжение, эмоциональные перегрузки;

- перенапряжение анализаторов (зрительных)

Оценка факторов производственной среды и трудового процесса приведена в таблице 1.

Таблица 1. Оценка факторов труда

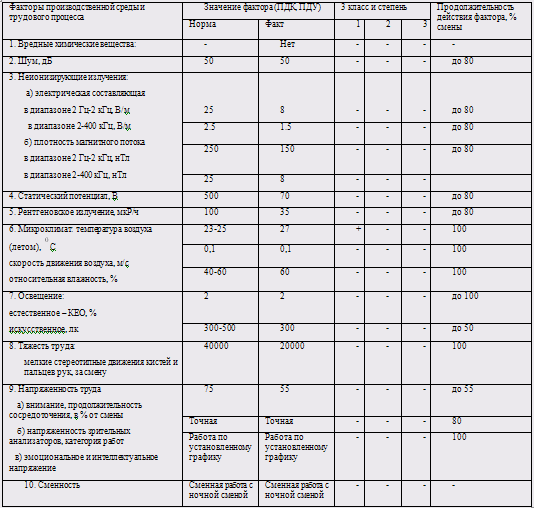
Из таблицы 1 видно, что в помещении несколько повышена температура воздуха. Это связано с избыточным выделением тепла. Поэтому доминирующим вредным фактором выберем повышенную температуру воздуха рабочей зоны.

3.2 Техника безопасности

Электроснабжение НИЛ осуществляется от трехфазной четырехпроводной сети с глухозаземленной нейтралью, ток переменный, частота 50 Гц, напряжение 220/380 В. Согласно требованиям ПУЭ и ГОСТ 12.1.030-81 выполнено зануление, повторное заземление нулевого провода, проводится контроль изоляции.

Для зануления электрически соединены на вводе в НИЛ с нулевым проводником сети корпуса всех ПЭВМ. Соединение выполнено нулевым защитным проводником, полная проводимость которого не менее 50% полной проводимости фазового провода. Для отключения поврежденного участка сети на вводе электросети в НИЛ установлен автомат защиты, ток срабатывания которого выбран по току короткого замыкания. Зануление превращает замыкание на корпус ПЭВМ в однофазное короткое замыкание, в результате чего срабатывает автомат защиты. Время отключения поврежденного участка сети не более 0,1-0,2 с.

Для уменьшения напряжения, приложенного к телу человека в момент замыкания, необходимо выполнено повторное заземление нулевого провода. Нулевой защитный проводник заземлен при помощи искусственных заземлителей. Сопротивление повторного заземления нулевого провода не превышает 30 Ом согласно требованию ПУЭ-85.

Не реже 1 раза в год при отключенном электропитании проводится контроль изоляции между нулем и фазой, нулевым защитным проводником и фазой, между фазами. Сопротивление изоляции не превышает 500 кОм.

Электросеть розеток для питания ПЭВМ проложена под съемным полом в гибких металлических рукавах.

Не применяются: самодельные удлинители, не соответствующие требованиям ПУЭ к переносным электропроводкам; не используется для отопления нестандартное электронагревательное оборудование; не используется поврежденные розетки, разветвители, коробки, выключатели и другие электроизделия.

Согласно требованиям ДНАОП 0.00-4.12-99 [25] проводятся вводный, первичный на рабочем месте, повторный, внеплановый и целевой инструктажи.

Вводный инструктаж проводится при поступлении на работу. Инструктаж организует и проводит служба охраны труда, факт инструктажа фиксируется в журнале вводного инструктажа.

Первичный инструктаж проводится непосредственно на рабочем месте. Факт инструктажа фиксируется в журнале первичного инструктажа. Аналогично с периодичностью 1 раз в 6 месяцев проводятся повторные инструктажи.

Внеплановый инструктаж проводится при изменении условий труда, введения в эксплуатацию новой техники, а также при несчастных случаях.

Целевой инструктаж в НИЛ проводится при выполнении работ, не связанных с их основными обязанностями.

Содержание всех инструктажей соответствует требованиям ДНАОП 0.00-4.12-99.

3.3 Производственная санитария и гигиена труда

Работы в НИЛ согласно ДНАОП 0.00-1.31-99 относятся к категории работ по энергозатратам организма легкая 1а - работы, производимые сидя и сопровождающиеся незначительным физическим напряжением. С целью создания нормальных условий для персонала установлены следующие нормы микроклимата по ГОСТ 12.0.005-88, приведенные в таблице 2.

Для обеспечения установленных (оптимальных) норм микроклимата в помещении НИЛ следует применять кондиционирование. Выполним расчет кондиционирования.

Таблица 2. Оптимальные нормы микроклимата

Время

года

Температура воздуха, град. С

Относительная влажность воздуха, %

Скорость движения

воздуха, м/с

Холодное

22-24

40-60

не более 0.1

Теплое

23-25

40-60

не более 0.1

Для обеспечения установленных норм микроклиматических параметров и чистоты воздуха в НИЛ применяют естественную вентиляцию и кондиционирование. Основной задачей установок кондиционирования воздуха (УКВ) является поддержание параметров воздушной среды в допустимых пределах, обеспечивающих надежную работу ПЭВМ и комфортные условия для обслуживающего персонала. Расчет вентиляции необходим для определения потребного воздухообмена (количества воздуха в единицу времени). Для определения требуемого воздухообмена необходимо определить общее тепловыделение в помещении НИЛ[26].

Тепло , излучаемое оборудованием, равно

Q_об = 860N₁ K₂ K₂ = 8600,80,951 = 654(ккал/ч),

(3.1)

где – суммарная мощность установленного оборудования;

– коэффициент использования мощностей, примем равным 0.95;

– коэффициент одновременной работы оборудования, с запасом примем равным 1.

Тепло , излучаемое людьми, равно

Q_л = 0,5ng = 0,52120 = 120 (ккал/ч),

(3.2)

где – количество работающих в помещении, 2 чел.;

– количество тепла, выделяемое человеком, при работе 1а равно 100-125 ккал/ч, примем равным 120 ккал/ч.

Тепло , излучаемое освещением, равно

Q_ос = k E S = 0,0530024 = 360 (ккал/ч),

(3.3)

где Е – наименьшая нормируемая освещенность, равна 300 кл;

S - площадь помещения, равна 24 кв.м.;

k – коэффициент тепловыделения,0,05 ккал/лк м² .

Тепло , выделяемое за счет солнечной радиации, равно:

Q_р = n_c k_c S = 8661,15 = 593,4 (ккал/ч),

(3.4)

где – удельное количество тепла, поступающего через единицу площади окна, равно 86 ккал/ч;

– поправочный коэффициент, зависит от географической полосы, для Харькова равен 1.15;

– площадь окон, равна 6 м² .

Общее выделение теплоты равно

Q = 654+120+360+593,4 = 1727,4 (ккал/ч) или 2 кВт.

(3.5)

Требуемый воздухообмен будет равен

L_тр = Q(1/(cr(t_п – t_к ))) = 1727,4(1/(0,24 1,29(27-18)) = 619 (м³ /ч)(3.6)

где – удельная теплоемкость воздуха, 0.24 ккал/кг·град;

– плотность воздуха, 1.29 кг/ м³ ;

– температура удаляемого воздуха, 27⁰ С;

– температура воздуха с кондиционера, 18⁰ С.

L_тр _. _ха = L_тр rc(t_внеш - t_уд )

L_{тр. ха} =6191,290,24 (32-18)=2683 (м³ /ч)

С учётом полученных результатов выбираем два кондиционера SamsungAW – 05EO.

Трудовая деятельность в НИЛ относится к группе В (отладка программ, перевод и редактирования и др.) [27]. Продолжительность работ превышает 4 ч и выполняемые работы относятся к III категории работ. Установлены перерывы по 20 мин каждый через 2 ч после начала работ, через 1,5 ч и 2, 5 ч после обеденного перерыва или же по 5-15 мин через каждый час работы. Общее время перерывов не превышает 60 мин.

Каждое рабочее место в НИЛ должно соответствует требованиям ДНАОП 0.00-1.31-99. Рабочие места расположены относительно световых проемов так, что естественный свет падает слева, при этом выдерживаются следующие расстояния:

от стен со световыми проемами до рабочего места - 1 м;

между тыльной поверхностью одного видеотерминала и экраном - 2,5 м.

Размещение рабочих мест в НИЛ показано на рисунке 2.

Рисунок 2. Схема размещения рабочих мест, оборудования и кондиционерови схема эвакуации при пожаре.

На рисунке 2. приведены следующие обозначения:

К1, К2 – кондиционеры, П1,П2 – рабочие места

3.4 Пожарная безопасность

Пожарная безопасность объекта - состояние объекта, при котором с регламентированной вероятностью исключается возможность возникновения условий и воздействия на людей опасных факторов пожара, а также обеспечивается защита материальных ценностей [28]. Причинами, которые могут вызвать пожар в рассматриваемом помещении, являются:

- неисправность электропроводки и приборов;

- короткое замыкание электрических цепей;

- перегрев аппаратуры и электропроводки;

- нарушение правил пожарной безопасности;

- разряд статического электричества;

- молния.

Помещение отдела по пожарной и взрывопожарной опасности относится к категории В согласно ОНТП 24-86, так как в обращении находятся твердые сгораемые вещества и материалы. Степень огнестойкости здания - П согласно СНиП 2.01.02-85, класс помещения по пожарной опасности П-IIа, согласно ПУЭ-87. Пожарная безопасность в соответствии с ГОСТ 12.1.004-91* и ДСТУ 2272-93 обеспечивается системами предотвращения пожара, противопожарной защиты. Организационно-техническими мероприятиями. Система предотвращения пожара:

- заземление корпусов для отвода заряда статистического электричества;

- контроль и профилактика изоляции;

- наличие плавких вставок и предохранителей в электронном оборудовании;

-наличие вентилятора для охлаждения электронной аппаратуры.

Для данного класса зданий и местности со средней грозовой деятельностью 10 и более грозовых часов в год, установлена Ш категория молниезащиты. РД 34.21.122-87.

Степень защиты, соответствующая классу помещения П-II-а IP44 для оборудования и IP2X для светильников. ПУЭ-87 [29].

Система противопожарной защиты:

- аварийное отключение и переключение аппаратуры;

- наличие первичных средств пожаротушения, огнетушителей ОУ-2А, из расчета 1 шт. на каждые 20 м² площади, так как углекислота обладает плохой электропроводностью;

- наличие системы автоматической пожарной сигнализации;

- дымовые извещатели из расчета 1 на 10 м² ;

- защита легковоспламеняющихся частей оборудования защитными материалами;

-использование негорючих материалов для акустической обработки стен и потолков.

Для успешной эвакуации персонала при пожаре размеры двери рабочего помещения предусмотрены следующими:

- ширина двери не менее 1,5 м;

- высота двери не менее 2,0 м;

- ширина коридора 1,8 м;

- рабочее помещение имеет два выхода;

-расстояние от самого удаленного рабочего места не превышает 100м. Организационные меры пожарной профилактики:

- обучение персонала правилам пожарной безопасности;

- издание необходимых инструкций и плакатов, плана эвакуации персонала в случае пожара.

3.5 Гражданская оборона

Т.к. разрабатываемый программный продукт производился в здании, вблизи которого не находятся потенциально опасные объекты, то разработка мер по защите персонала в чрезвычайных ситуациях не производилась.

3.6 Защита окружающей среды

Т.к. разрабатываемый программный продукт не наносит вред окружающей среде, меры защиты в данной дипломной работе не рассматривались.

Выводы

С развитием и постоянным внедрением компьютерных телекоммуникаций в различные сферы человеческой деятельности (научные исследования, электронная коммерция, банковское дело, медицина и т.д.) все более остро встает вопрос безопасного обмена данными через незащищенные каналы передачи. Единственным эффективным средством защиты информации остается ее криптографическое преобразование.

Актуальность данной разработки, обусловлен постоянно повышающимся интересом мирового сообщества к проблемам защиты информации - ее конфиденциальности и аутентичности.

В процессе анализа проблемной области были подвергнуты серьезному изучению математический аппарат шифра, критерии его применения, а также проблемы реализации на современных микропроцессорных архитектурах.

В ходе работы был реализован перечень основных научных, организационных и практических задач, требующих решения в процессе достижения цели дипломного проектирования, а именно:

-изучить методику применения интегральной атаки против блочного симметричного шифра Crypton,

-адаптировать методику применения интегральной атаки для использования против усеченного варианта блочного симметричного шифра Crypton,

-выполнить программную реализацию зашифрования, расшифрования и интегральной атаки против усеченного вариантаблочного симметричного шифра Crypton.

В ходе работы дипломного проекта был сделан программный продукт.

Программа разрабатывалась на языке C++, финальная сборка была произведена в среде разработки BorlandC++ v 3.1.

К основным операциям разработанным в ходе дипломного проектирования программного продукта можно отнести:

-практическое решение задач шифрования и расшифрования данных по алгоритму Crypton;

- реализация интегральной атаки на усеченный вариант шифра Crypton.

Возможными направлениями продолжения работ дипломного проекта можно рассматривать:

-расширение функциональности программного продукта в части увеличения детализации управления элементами алгоритма шифрования;

введение статистических средств анализа;

-распространение разработанных методик изучения криптографического алгоритма Crypton на другие современные алгоритмы шифрования.

В результате разработанных в разделе Безопасность жизнедеятельности организационных и технических мероприятий факторы производственной среды и трудового процесса в НИЛ стали находится в пределах допустимых условий труда. Технический и организационный уровень рабочего места обеспечивает безопасность человека. Дополнительных рекомендаций по улучшению условий труда не требуется.

Приложение А

шифр атака криптографический crypton

Файл encrdecr.cpp

#include stdio.h

#include string.h

#include conio.h

#include io.h

#include fcntl.h

#include iostream.h

#include sys/stat.h

#include stdlib.h

#include std_defs.h

#include crypton.h

#include atack.h

void atack(int);

int main()

{

clrscr();

int i,q,f1,f2;

char f_nam1[111];

char f_nam2[111];

char f_nam3[111];

char w;

union

{

u1byte a1[4][4];

u4byte a4[4];

}

st,st1,st2,k;

for(i=0;i4;i++)

k.a4[i]=0;

set_key(k.a4,128);

printf(encript/decrypt/atack(0/1/2)?);

cout\n;

w=getch();

if((w!=0)(w!=1)(w!=2))

exit(3);

if(w==2)

{

coutEnter name of atacking file\n;

gets(f_nam3);

f2=open(f_nam3,O_RDONLY|O_BINARY);

if(f2==-1)

{

close(f2);

exit(1);

}

atack(f2);

}

if(w==0)

{

coutEnter name of opening file\n;

gets(f_nam1);

coutEnter name of encription file\n;

gets(f_nam2);

f1=open(f_nam1,O_RDONLY|O_BINARY);

if(f1==-1)

{ // perror(f_nam1);

puts(f_nam1);

cout\n;

puts(f_nam2);

close(f1);

exit(1);

}

f2=open(f_nam2,O_WRONLY|O_CREAT|O_TRUNC|O_BINARY,S_IWRITE);

if(f2==-1)

{

close(f2);

exit(2);

}

{

q=read(f1,st.a1[0][0],16);

if(q==16)

{

encrypt(st.a4, st1.a4);

write(f2,st1.a1[0][0],16);

}

else

{

if(q0)

{

for(i=0;i4;i++)

st2.a4[i]=0;

for(i=0;iq;i++)

{

st2.a1[i/4][i%4]=st.a1[i/4][i%4];

}

encrypt(st2.a4,st1.a4);

write(f2,st1.a1[0][0],16);

}

while(q==16);

close(f1);

close(f2);

}

if(w==1)

{

coutEnter name of encription file\n;

gets(f_nam2);

coutEnter name of decription file\n;

gets(f_nam3);

f1=open(f_nam2,O_RDONLY|O_BINARY);

if(f1==-1)

{

close(f1);

exit(1);

}

f2=open(f_nam3,O_WRONLY|O_CREAT|O_TRUNC|O_BINARY,S_IWRITE);

if(f2==-1)

{

close(f2);

exit(2);

}

{

q=read(f1,st.a1[0][0],16);

if(q==16)

{

decrypt(st.a4, st1.a4);

write(f2,st1.a1[0][0],16);

}

else

{

if(q0)

{

for(i=0;i4;i++)

st2.a4[i]=0;

for(i=0;iq;i++)

{

st2.a1[i/4][i%4]=st.a1[i/4][i%4];

}

decrypt(st2.a4,st1.a4);

write(f2,st1.a1[0][0],16);

}

while(q==16);

close(f1);

close(f2);

}

return 0;

}

Файл crypton.h

#include std_defs.h

static char *alg_name[] = { crypton, crypton.c };

char **cipher_name()

{

return alg_name;

}

#define gamma_tau(x,b,m,p,q) \

(x) = (((u4byte)s_box[p][byte(b[0],m)] ) | \

((u4byte)s_box[q][byte(b[1],m)] 8) | \

((u4byte)s_box[p][byte(b[2],m)] 16) | \

((u4byte)s_box[q][byte(b[3],m)] 24))

#define ma_0 0x3fcff3fc

#define ma_1 0xfc3fcff3

#define ma_2 0xf3fc3fcf

#define ma_3 0xcff3fc3f

#define mb_0 0xcffccffc

#define mb_1 0xf33ff33f

#define mb_2 0xfccffccf

#define mb_3 0x3ff33ff3

#define pi(b,n0,n1,n2,n3) \

(((b)[0] ma_##n0) ^ \

((b)[1] ma_##n1) ^ \

((b)[2] ma_##n2) ^ \

((b)[3] ma_##n3))

#define phi_n(x,n0,n1,n2,n3) \

( (x) mb_##n0) ^ \

(rotl((x), 8) mb_##n1) ^ \

(rotl((x), 16) mb_##n2) ^ \

(rotl((x), 24) mb_##n3)

#define phi_00(x) phi_n(x,0,1,2,3)

#define phi_01(x) phi_n(x,3,0,1,2)

#define phi_02(x) phi_n(x,2,3,0,1)

#define phi_03(x) phi_n(x,1,2,3,0)

#define phi_10(x) phi_n(x,3,0,1,2)

#define phi_11(x) phi_n(x,2,3,0,1)

#define phi_12(x) phi_n(x,1,2,3,0)

#define phi_13(x) phi_n(x,0,1,2,3)

#define phi0(x,y) \

(y)[0] = phi_00((x)[0]); \

(y)[1] = phi_01((x)[1]); \

(y)[2] = phi_02((x)[2]); \

(y)[3] = phi_03((x)[3])

#define phi1(x,y) \

(y)[0] = phi_10((x)[0]); \

(y)[1] = phi_11((x)[1]); \

(y)[2] = phi_12((x)[2]); \

(y)[3] = phi_13((x)[3])

u1byte p_box[3][16] =

{ { 15, 9, 6, 8, 9, 9, 4, 12, 6, 2, 6, 10, 1, 3, 5, 15 },

{ 10, 15, 4, 7, 5, 2, 14, 6, 9, 3, 12, 8, 13, 1, 11, 0 },

{ 0, 4, 8, 4, 2, 15, 8, 13, 1, 1, 15, 7, 2, 11, 14, 15 }

};

u4byte tab_gen = 0;

u1byte s_box[2][256];

u4byte s_tab[4][256];

u4byte l_key[104];

u4byte *e_key = l_key + 52;

u4byte *d_key = l_key;

void gen_tab(void)

{ u4byte i, xl, xr, yl, yr;

for(i = 0; i 256; ++i)

{

xl = (i 0xf0) 4; xr = i 15;

yr = xr ^ p_box[1][xl ^ p_box[0][xr]];

yl = xl ^ p_box[0][xr] ^ p_box[2][yr];

yr |= (yl 4); s_box[0][i] = (u1byte)yr; s_box[1][yr] = (u1byte)i;

xr = yr * 0x01010101; xl = i * 0x01010101;

s_tab[0][ i] = xr 0x3fcff3fc;

s_tab[1][yr] = xl 0xfc3fcff3;

s_tab[2][ i] = xr 0xf3fc3fcf;

s_tab[3][yr] = xl 0xcff3fc3f;

}

};

/* initialise the key schedule from the user supplied key */

u4byte kp[4] = { 0xbb67ae85, 0x3c6ef372, 0xa54ff53a, 0x510e527f };

u4byte kq[4] = { 0x9b05688c, 0x1f83d9ab, 0x5be0cd19, 0xcbbb9d5d };

#define h0_block(n,r0,r1) \

e_key[4 * n + 8] = rotl(e_key[4 * n + 0], r0); \

e_key[4 * n + 9] = rc ^ e_key[4 * n + 1]; \

e_key[4 * n + 10] = rotl(e_key[4 * n + 2], r1); \

e_key[4 * n + 11] = rc ^ e_key[4 * n + 3]

#define h1_block(n,r0,r1) \

e_key[4 * n + 8] = rc ^ e_key[4 * n + 0]; \

e_key[4 * n + 9] = rotl(e_key[4 * n + 1], r0); \

e_key[4 * n + 10] = rc ^ e_key[4 * n + 2]; \

e_key[4 * n + 11] = rotl(e_key[4 * n + 3], r1)

u4byte *set_key(const u4byte in_key[], const u4byte key_len)

{ u4byte i, rc, t0, t1, tmp[4];

if(!tab_gen)

{

gen_tab(); tab_gen = 1;

}

e_key[2] = e_key[3] = e_key[6] = e_key[7] = 0;

switch((key_len + 63) / 64)

{

case 4: e_key[3] = in_key[6]; e_key[7] = in_key[7];

case 3: e_key[2] = in_key[4]; e_key[6] = in_key[5];

case 2: e_key[0] = in_key[0]; e_key[4] = in_key[1];

e_key[1] = in_key[2]; e_key[5] = in_key[3];

}

tmp[0] = pi(e_key, 0, 1, 2, 3) ^ kp[0];

tmp[1] = pi(e_key, 1, 2, 3, 0) ^ kp[1];

tmp[2] = pi(e_key, 2, 3, 0, 1) ^ kp[2];

tmp[3] = pi(e_key, 3, 0, 1, 2) ^ kp[3];

gamma_tau(e_key[0], tmp, 0, 0, 1);

gamma_tau(e_key[1], tmp, 1, 1, 0);

gamma_tau(e_key[2], tmp, 2, 0, 1);

gamma_tau(e_key[3], tmp, 3, 1, 0);

tmp[0] = pi(e_key + 4, 1, 2, 3, 0) ^ kq[0];

tmp[1] = pi(e_key + 4, 2, 3, 0, 1) ^ kq[1];

tmp[2] = pi(e_key + 4, 3, 0, 1, 2) ^ kq[2];

tmp[3] = pi(e_key + 4, 0, 1, 2, 3) ^ kq[3];

gamma_tau(e_key[4], tmp, 0, 1, 0);

gamma_tau(e_key[5], tmp, 1, 0, 1);

gamma_tau(e_key[6], tmp, 2, 1, 0);

gamma_tau(e_key[7], tmp, 3, 0, 1);

t0 = e_key[0] ^ e_key[1] ^ e_key[2] ^ e_key[3];

t1 = e_key[4] ^ e_key[5] ^ e_key[6] ^ e_key[7];

e_key[0] ^= t1; e_key[1] ^= t1;

e_key[2] ^= t1; e_key[3] ^= t1;

e_key[4] ^= t0; e_key[5] ^= t0;

e_key[6] ^= t0; e_key[7] ^= t0;

rc = 0x01010101;

h0_block( 0, 8, 16); h1_block(1, 16, 24); rc = 1;

h1_block( 2, 24, 8); h0_block(3, 8, 16); rc = 1;

h0_block( 4, 16, 24); h1_block(5, 24, 8); rc = 1;

h1_block( 6, 8, 16); h0_block(7, 16, 24); rc = 1;

h0_block( 8, 24, 8); h1_block(9, 8, 16); rc = 1;

h1_block(10, 16, 24);

for(i = 0; i 13; ++i)

{

if(i 1)

{

phi0(e_key + 4 * i, d_key + 48 - 4 * i);

}

else

{

phi1(e_key + 4 * i, d_key + 48 - 4 * i);

}

phi1(e_key + 48, e_key + 48);

phi1(d_key + 48, d_key + 48);

return l_key;

};

/* encrypt a block of text */

#define fr0(i,k) \

b1[i] = s_tab[ (i) ][byte(b0[0],i)] ^ \

s_tab[((i) + 1) 3][byte(b0[1],i)] ^ \

s_tab[((i) + 2) 3][byte(b0[2],i)] ^ \

s_tab[((i) + 3) 3][byte(b0[3],i)] ^ (k)

#define fr1(i,k) \

b0[i] = s_tab[((i) + 1) 3][byte(b1[0],i)] ^ \

s_tab[((i) + 2) 3][byte(b1[1],i)] ^ \

s_tab[((i) + 3) 3][byte(b1[2],i)] ^ \

s_tab[(i) ][byte(b1[3],i)] ^ (k)

#define f0_rnd(kp) \

fr0(0,(kp)[0]); fr0(1,(kp)[1]); \

fr0(2,(kp)[2]); fr0(3,(kp)[3])

#define f1_rnd(kp) \

fr1(0,(kp)[0]); fr1(1,(kp)[1]); \

fr1(2,(kp)[2]); fr1(3,(kp)[3])

void encrypt(const u4byte in_blk[4], u4byte out_blk[4])

{ u4byte b0[4], b1[4];

b0[0] = in_blk[0] ^ e_key[0];

b0[1] = in_blk[1] ^ e_key[1];

b0[2] = in_blk[2] ^ e_key[2];

b0[3] = in_blk[3] ^ e_key[3];

f0_rnd(e_key + 4); f1_rnd(e_key + 8);

f0_rnd(e_key + 12); f1_rnd(e_key + 16);

f0_rnd(e_key + 20); f1_rnd(e_key + 24);

f0_rnd(e_key + 28); f1_rnd(e_key + 32);

f0_rnd(e_key + 36); f1_rnd(e_key + 40);

f0_rnd(e_key + 44);

gamma_tau(b0[0], b1, 0, 1, 0);

gamma_tau(b0[1], b1, 1, 0, 1);

gamma_tau(b0[2], b1, 2, 1, 0);

gamma_tau(b0[3], b1, 3, 0, 1);

out_blk[0] = b0[0] ^ e_key[48];

out_blk[1] = b0[1] ^ e_key[49];

out_blk[2] = b0[2] ^ e_key[50];

out_blk[3] = b0[3] ^ e_key[51];

};

/* decrypt a block of text */

void decrypt(const u4byte in_blk[4], u4byte out_blk[4])

{ u4byte b0[4], b1[4];

b0[0] = in_blk[0] ^ d_key[0];

b0[1] = in_blk[1] ^ d_key[1];

b0[2] = in_blk[2] ^ d_key[2];

b0[3] = in_blk[3] ^ d_key[3];

f0_rnd(d_key + 4); f1_rnd(d_key + 8);

f0_rnd(d_key + 12); f1_rnd(d_key + 16);

f0_rnd(d_key + 20); f1_rnd(d_key + 24);

f0_rnd(d_key + 28); f1_rnd(d_key + 32);

f0_rnd(d_key + 36); f1_rnd(d_key + 40);

f0_rnd(d_key + 44);

gamma_tau(b0[0], b1, 0, 1, 0);

gamma_tau(b0[1], b1, 1, 0, 1);

gamma_tau(b0[2], b1, 2, 1, 0);

gamma_tau(b0[3], b1, 3, 0, 1);

out_blk[0] = b0[0] ^ d_key[48];

out_blk[1] = b0[1] ^ d_key[49];

out_blk[2] = b0[2] ^ d_key[50];

out_blk[3] = b0[3] ^ d_key[51];

}

Файл STD_DEFS.H

/* 1. Standard types for AES cryptography source code */

typedef unsigned char u1byte; /* an 8 bit unsigned character type */

typedef unsigned short u2byte; /* a 16 bit unsigned integer type */

typedef unsigned long u4byte; /* a 32 bit unsigned integer type */

typedef signed char s1byte; /* an 8 bit signed character type */

typedef signed short s2byte; /* a 16 bit signed integer type */

typedef signed long s4byte; /* a 32 bit signed integer type */

/* 2. Standard interface for AES cryptographic routines */

/* These are all based on 32 bit unsigned values and will therefore */

/* require endian conversions for big-endian architectures */

#ifdef __cplusplus

extern C

{

#endif

char **cipher_name(void);

u4byte *set_key(const u4byte in_key[], const u4byte key_len);

void encrypt(const u4byte in_blk[4], u4byte out_blk[4]);

void decrypt(const u4byte in_blk[4], u4byte out_blk[4]);

#ifdef __cplusplus

};

#endif

/* 3. Basic macros for speeding up generic operations */

/* Circular rotate of 32 bit values */

#ifdef _MSC_VER

# include stdlib.h

# pragma intrinsic(_lrotr,_lrotl)

# define rotr(x,n) _lrotr(x,n)

# define rotl(x,n) _lrotl(x,n)

#else

#define rotr(x,n) (((x) ((int)(n))) | ((x) (32 - (int)(n))))

#define rotl(x,n) (((x) ((int)(n))) | ((x) (32 - (int)(n))))

#endif

/* Invert byte order in a 32 bit variable */

#define bswap(x) (rotl(x, 8) 0x00ff00ff | rotr(x, 8) 0xff00ff00)

/* Extract byte from a 32 bit quantity (little endian notation) */

#define byte(x,n) ((u1byte)((x) (8 * n)))

/* For inverting byte order in input/output 32 bit words if needed */

#ifdef BLOCK_SWAP

#define BYTE_SWAP

#define WORD_SWAP

#endif

#ifdef BYTE_SWAP

#define io_swap(x) bswap(x)

#else

#define io_swap(x) (x)

#endif

/* For inverting the byte order of input/output blocks if needed */

#ifdef WORD_SWAP

#define get_block(x) \

((u4byte*)(x))[0] = io_swap(in_blk[3]); \

((u4byte*)(x))[1] = io_swap(in_blk[2]); \

((u4byte*)(x))[2] = io_swap(in_blk[1]); \

((u4byte*)(x))[3] = io_swap(in_blk[0])

#define put_block(x) \

out_blk[3] = io_swap(((u4byte*)(x))[0]); \

out_blk[2] = io_swap(((u4byte*)(x))[1]); \

out_blk[1] = io_swap(((u4byte*)(x))[2]); \

out_blk[0] = io_swap(((u4byte*)(x))[3])

#define get_key(x,len) \

((u4byte*)(x))[4] = ((u4byte*)(x))[5] = \

((u4byte*)(x))[6] = ((u4byte*)(x))[7] = 0; \

switch((((len) + 63) / 64)) { \

case 2: \

((u4byte*)(x))[0] = io_swap(in_key[3]); \

((u4byte*)(x))[1] = io_swap(in_key[2]); \

((u4byte*)(x))[2] = io_swap(in_key[1]); \

((u4byte*)(x))[3] = io_swap(in_key[0]); \

break; \

case 3: \

((u4byte*)(x))[0] = io_swap(in_key[5]); \

((u4byte*)(x))[1] = io_swap(in_key[4]); \

((u4byte*)(x))[2] = io_swap(in_key[3]); \

((u4byte*)(x))[3] = io_swap(in_key[2]); \

((u4byte*)(x))[4] = io_swap(in_key[1]); \

((u4byte*)(x))[5] = io_swap(in_key[0]); \

break; \

case 4: \

((u4byte*)(x))[0] = io_swap(in_key[7]); \

((u4byte*)(x))[1] = io_swap(in_key[6]); \

((u4byte*)(x))[2] = io_swap(in_key[5]); \

((u4byte*)(x))[3] = io_swap(in_key[4]); \

((u4byte*)(x))[4] = io_swap(in_key[3]); \

((u4byte*)(x))[5] = io_swap(in_key[2]); \

((u4byte*)(x))[6] = io_swap(in_key[1]); \

((u4byte*)(x))[7] = io_swap(in_key[0]); \

}

#else

#define get_block(x) \

((u4byte*)(x))[0] = io_swap(in_blk[0]); \

((u4byte*)(x))[1] = io_swap(in_blk[1]); \

((u4byte*)(x))[2] = io_swap(in_blk[2]); \

((u4byte*)(x))[3] = io_swap(in_blk[3])

#define put_block(x) \

out_blk[0] = io_swap(((u4byte*)(x))[0]); \

out_blk[1] = io_swap(((u4byte*)(x))[1]); \

out_blk[2] = io_swap(((u4byte*)(x))[2]); \

out_blk[3] = io_swap(((u4byte*)(x))[3])

#define get_key(x,len) \

((u4byte*)(x))[4] = ((u4byte*)(x))[5] = \

((u4byte*)(x))[6] = ((u4byte*)(x))[7] = 0; \

switch((((len) + 63) / 64)) { \

case 4: \

((u4byte*)(x))[6] = io_swap(in_key[6]); \

((u4byte*)(x))[7] = io_swap(in_key[7]); \

case 3: \

((u4byte*)(x))[4] = io_swap(in_key[4]); \

((u4byte*)(x))[5] = io_swap(in_key[5]); \

case 2: \

((u4byte*)(x))[0] = io_swap(in_key[0]); \

((u4byte*)(x))[1] = io_swap(in_key[1]); \

((u4byte*)(x))[2] = io_swap(in_key[2]); \

((u4byte*)(x))[3] = io_swap(in_key[3]); \

}

#endif

#define beg /*

#define en */

Файл АTACK.H

#ifndef ATACH.H_H #define ATACH.H_H

#define ENCRYPT 0 #define DECRYPT 1

¦include StdAfx.h #include Resource.h ¦include winaesDlg.h

¦define ROTL(x) ( ( (x) 7) | ( (x) 1) )

¦define R0TL8 (x) ( ( (x) 8) | ( (x) 24) ) ¦define R0TL16(x) ( ( (x) 16) I ( (x) 16) ) ¦define ROTL24 (x) ( ( (x) 24) | ( (x) 8) )

int KeyExpansion(CWinaesDlg* dig, int nb,int nk, BYTE* key); void Encrypt(CWinaesDlg* dig, BYTE* buff, BYTE* result); void InvDecrypt(CWinaesDlg* dig, BYTE* buff, BYTE* result); void EquDecrypt(CWinaesDlg* dig, BYTE* buff, BYTE* result);

int blockEncrypt(CWinaesDlg* dig, BYTE *input, int inputLen, BYTE* result, int cipher_mode); int blockDecrypt(CWinaesDlg* dig, BYTE *input, int inputLen, BYTE* result, int decrypt_mode, int cipher_mode);

¦endif

ATACH.H.CPP

¦include stdio.h ¦include stdlib.h ¦include Rijndael.h ¦include service.h

¦define BPOLY (BYTE) Oxllb ¦define MPOLY (BYTE) 0x101

BYTE Co[4]={0x3,0xl,0xl,0x2};

BYTE InvCo[4]={0xB,0xD,0x9,0xE};

int N, Nk, Nb, Nr;

DWORD fkey[120];

DWORD ikey[120]; // inverse key

DWORD ekey[120]; // equivalent key

BYTE subbytes[256] ; BYTE invsubbytes[256] ;

BYTE shfts[3][4];

static char strTmp[260], Tmp[260]; static DWORD s[8];

void ResetShifts() {

for (int i=0; i3; i++)

for (int j=0; j4; j++)

if (i==2 j==3) shfts[i][j]=4; else shfts[i][j]=j;

void shiftrow(BYTE* row, int n, int direct)

BYTE t; int j ;

if (n)

for (int i=0; in; i++) switch (direct)

case ENCRYPT:

t=row[0];

for (j=l; jNb; j++) row[j-l]=row[j] ; row [Nb-1 In¬break;

case DECRYPT:

t=row[Nb-l];

for (j = Nb-1; j0; j--) row[j]=row[j-1] ,

row[0]=t;

break;

void ShifRows(BYTE* s, int direct)

BYTE temp[8]; int i, j;

for (i=0;i4;i++)

for (j=0;jNb;j++) temp[j]=s[j*4+i];

shiftrow( temp, shfts[Nb/2-2][i], direct),

for (j=0;jNb;j++) s[j*4+i]=temp[j]; }

static DWORD pack(BYTE *b)

{

return ( (DWORD)b[3]24) | ( (DWORD)b [2] 16) | ( (DWORD) b [1 ] 8) | (DWORD)b[0],

static void unpack(DWORD a,BYTE *b) {

b[0] = (BYTE)a;

b[l] = (BYTE) (a8) ;

b[2] = (BYTE) (a16) ;

b[3] = (BYTE) (a24) ; }

static BYTE xtime(BYTE a, BYTE mod) {

return ( ( a 0x80) ? alAmod

static BYTE add (BYTE a, BYTE b) {return алЬ;}

static BYTE bmul(BYTE a,BYTE b, BYTE mod) {

BYTE t,s, u;

u=b; t=a; s=0;

while (u) {

if(u 1) эл=Ь;

u=l ;

t=xtime(t, mod);

return (s); }

static BYTE square(BYTE a, BYTE mod) {

return (bmul(a,a, mod)); }

static BYTE product(DWORD x,DWORD y, BYTE mod) {

BYTE xb [ 4 ] , yb [ 4 ] ;

unpack(x,xb);

unpack(y,yb);

return bmul(xb[0],yb[0], mod)лЬти1(xb[1],yb[1], mod)лЬти1(xb[2],yb[2], mod)лЬти1(xb[3],yb[3], mod) ; }

static BYTE finv(const BYTE x, BYTE mod) {

BYTE result = x;

for (int i=l; i7; i++) result = bmul(square(result , mod), x, mod);

return square(result, mod); }

BYTE SBinvModulo; BYTE SBmulModulo; BYTE SBmulConstl; BYTE SBmulConst2; BYTE SBaddConstl; BYTE SBaddConst2;

static BYTE ByteSubOLD(BYTE x) BYTE result=x;

result = finv( result , SBinvModulo);

result = bmul( SBmulConstl, result, SBmulModulo);

result = add( result, SBaddConstl);

return result; }

static BYTE InvByteSubOLD(BYTE x) BYTE result=x;

result = bmul( SBmulConst2, result, SBmulModulo); result = add(result, SBaddConst2); result = finv( result, SBinvModulo); return result;

void FillTables(int mode)

for (int i=0; i256;

if (mode 1) subbytes[i]= ByteSubOLD(i);

if (mode 2) invsubbytes[i]= InvByteSubOLD(i)

void ResetTables()

Encrypt(dig, iv, block);

for (1 = k; (1 (k + OFB_bits)) (1 (Nb5) ) ; 1++) {

result[1 3] = (block[0] 0x80U) (1 7);

for (j = 0; j (Nb2)-1; j++) {

iv[j] = iv[j] 1) | (iv[j + 1] 7);

block[j] = (block[j] 1) | (block[j + 17);

1] 1) | ((block[0] 0x80U) 7 );

} }

if (OFB_Debug) {

CharStr2HexStr((BYTE*)input, Tmp, Nb*4); sprintf(strTmp, in[%04u]=%s, i, Tmp); dlg-m_eDebug.AddString(strTmp);

CharStr2HexStr((BYTE*)result, Tmp, Nb*4); sprintf(strTmp,out[%04u]=%s, i, Tmp); dlg-m_eDebug.AddString(strTmp); }

result += Nb2;

input += Nb2; }

free(iv); break;

case MODE_CTR:

iv = (BYTE*) malloc(Nb2) ; memcpy(iv, cipher_IV, Nb2);

for (i = 1; i = numBlocks; i++) {

if (CTR_Debug) {

//CharStr2HexStr((BYTE*)s, Tmp, Nb*4);

sprintf(strTmp,= CTR AES Nb=%u Nk=%u, block %04u encrypt ======================, Nb, Nk, i);

dlg-m_eDebug.AddString(strTmp);

CharStr2HexStr((BYTE*)iv, Tmp, Nb*4); sprintf(strTmp, IV[%04u]=%s, i, Tmp); dlg-m_eDebug.AddString(strTmp); }

Encrypt(dig, iv, result);

for (j=0; j Nb; j++) ((DWORD*)result)[j] л= ((DWORD*)input)[j];

increase_counter ( iv, Nb2);

if (CTR_Debug) {

CharStr2HexStr((BYTE*)input, Tmp, Nb*4);

sprintf(strTmp, in[%04u]=%s, i, Tmp);

dlg-m_eDebug.AddString(strTmp);

CharStr2HexStr((BYTE*)result, Tmp, Nb*4); sprintf(strTmp,out[%04u]=%s, i, Tmp); dlg-m_eDebug.AddString(strTmp); }

input += Nb2; result += Nb2; }

free(iv); break; default:

return BAD_CIPHER_STATE; }

return 128*numBlocks;

Скачать архив с текстом документа