Использование анализа чувствительности реагирования в процессе оценки риска инвестиционного проекта
СОДЕРЖАНИЕ: Методы количественного анализа рисков проекта: анализ чувствительности (уязвимости), сценариев и имитационное моделирование рисков по методу Монте-Карло. Классификация факторов, варьируемых в процессе, и экономико-математическая сущность анализа.Использование анализа чувствительности реагирования в процессе оценки риска инвестиционного проекта.
Наиболее часто встречающимися методами количественного анализа рисков проекта, являются анализ чувствительности (уязвимости), анализ сценариев и имитационное моделирование рисков по методу Монте-Карло.
Проведение количественного анализа проектных рисков опирается на базисный вариант расчета проекта. Задача количественного анализа состоит в численном измерении влияния изменений рискованных факторов на эффективность проекта.
Анализ чувствительности (уязвимости) происходит при последовательно-единичном изменении каждой переменной: только одна из переменных меняет значение, на основе чего пересчитывается новое значение используемого критерия (например, критерия чистого дисконтированного дохода NPV). Затем оценивается процентное изменение критерия по сравнению с базисным случаем и рассчитывается показатель чувствительности, представляющий собой отношение процентного изменения критерия к изменению значения переменной на один процент (так называемая эластичность изменения показателя). Таким же образом исчисляются показатели чувствительности по каждой из остальных переменных.
По результатам этих расчетов происходят экспертное ранжирование переменных по степени важности (например, очень высокая, средняя, невысокая) и экспертная оценка прогнозируемости (предсказуемости) значений переменных (например, высокая, средняя, низкая)· Далее эксперт строит матрицу чувствительности, позволяющую выделить наименее и наиболее рискованные для проекта переменные (показатели).
Анализ чувствительности — простейший и поэтому наиболее используемый количественный метод исследования рисков. Однако в его простоте кроются некоторые недостатки:
во-первых, этот метод является экспертным, т.е. разные группы экспертов могуг получить различные результаты;
во-вторых, в ходе анализа чувствительности не учитывается связь (корреляция) между изменяемыми переменными.
Цель анализа чувствительности — выявить важнейшие факторы, так называемые критические переменные, способные наиболее серьезно повлиять на проект и проверить воздействие последовательных (одиночных) изменений этих факторов на результаты проекта. В теории эксперимента анализ чувствительности называют однофакторным анализом. Результаты проведенного ранее качественного анализа рисков проекта являются базой, фундаментом при отборе факторов для количественного анализа.
Классификация факторов, варьируемых в процессе анализа чувствительности:
первая группа — факторы, влияющие на обьем доходов (выгод) проекта;
вторая группа — факторы, влияющие на объем проектных затрат.
Варьируемые факторы, рассматриваемые на практике:
-показатели инфляции;
-физический объем продаж как следствие емкости рынка, доли предприятия на рынке, потенциала роста рыночного спроса;
-переменные издержки;
-постоянные издержки;
-требуемый объем инвестиций;
-стоимость привлекаемого капитала в завиеимости от условий и источников его формирования (например, процент за кредиты).
В инвестиционном проектировании анализ чувствительности играет важную роль для учета неопределенности и выделения факторов, которые могут повлиять на успешный результат проекта. Кроме того, анализ чувствительности лежит в основе принятия ряда управленческих решений. Так, например, если цена продукта оказалась критическим фактором, то можно усилить программу маркетинга или пересмотреть затратную часть, чтобы снизить стоимость проекта. Если же проведенный количественный анализ рисков проекта выявит его высокую чувствительность к изменению объема производства, то следует уделить внимание мерам по повышению производительности, например, обучению персонала менеджменту и др.
В формировании денежного потока проекта, а следовательно, и в расчете его критериев эффективности участвуют многие факторы и позитивного (доходного), и негативного (расходного) характера с точки зрения конечной результативности проекта. В качестве примера рассмотрим некоторые из факторов, учет изменения которых необходим при проведении анализа чувствительности.
К позитивным факторам прежде всего можно отнести: задержку оплаты за поставленное сырье, материалы, комплектующие, а также период времени поставки продукции с момента получения авансового платежа при реализации продукции или услуг на условиях предоплаты. Однако задержка оплаты за сырье имеет позитивное влияние на результат только в том случае, если цена материалов и комплектующих определяется на дату поставки и соответствует текущему уровню цен. Важной является группа факторов, связанная с формированием и управлением запасами. Объектом анализа должны стать факторы, характеризующие условия формирования капитала.
Анализ точки безубыточности, широко используемый в международной практике — простейший способ, позволяющий проводить грубую оценку риска проекта по методу чувствительности.
В качестве другого способа анализа чувствительности проекта можно использовать задачу математического программирования.
Рассмотрим простой пример, иллюстрирующий возможности использования методов математического программирования для решения задачи организации бизнеса и анализа проектных рисков.
Пример. Некий бизнесмен решил создать компанию, сдающую в аренду клиентам офисное оборудование (например, факсы и ксероксы), которое он предполагает закупить. Предположим (для простоты), что каждый договор с клиентом об аренде имеет длительность два года и заключается в момент закупки оборудования компанией, т.е. в начале первого года. Проведенный компанией анализ рынка позволяет утверждать, что существует неограниченный спрос на предлагаемое в аренду оборудование по стандартной арендной плате, общая сумма которой будет выплачена в конце второго года. Чистый дисконтированный доход, полученный бизнесменом от сдачи в аренду каждого факса и каждого ксерокса, составит 400 и 500 ден. ед, соответственно. Стоимость факса 300 ден. ед., из которых часть (100 ден. ед.) выплачивается в конце первого года, а остальная сумма (200ден.ед.) — в конце второго, ксерокс стоит 400 ден. ед., и схема выплат аналогична:
300 ден, ед, выплачиваются в конце первого года, а остальная сумма (100 ден.ед,) — в конце второго. Бизнесмен предполагает, что доступные ему ежегодные фонды ограничены и составляют 40 000 ден. ед. (в первый год) и 30 000 ден. ед. (во второй год).
Какое количество факсов и ксероксов следует приобрести бизнесмену, чтобы максимизировать суммарный чистый дисконтированный доход проекта?
Ответ на вопрос данной задачи можно получить с помощью методов линейного программирования.
Для построения модели задачи обозначим число единиц оборудования, которое нужно приобрести:
f — число факсов;
х — число ксероксов.
Введем ограничения:
100 f+ 300х 40 000; (1)
200 f + 100х 30 000. (2)
Экономический смысл построенных ограничений (1), (2) состоит в том, что ежегодные суммарные выплаты за приобретенные бизнесменом факсы и ксероксы не могут превышать размеров доступных ему ежегодных фондов. Кроме того, для реальных экономических величин должны выполняться ограничения:
f 0 (3)
х 0 (4)
Требуется максимизировать функцию
Z = 400 f+ 500 х (5)
при ограничениях (1)—(4).
Известно, что в случае двух переменных решение задачи математического программирования можно провести не только аналитически (например, используя симплекс-метод), но и графически. В нашем примере интерес представляет только целочисленное решение.
Рассмотрим графический вариант решения модели сконструированной по выражениям (1)—(5).
Заменив неравенство (1) равенством, построим в декартовой системе координат соответствующую прямую 1 (рис.1). Она разделит плоскость на две полуплоскости, расположенные над и под прямой. Неравенству (1) будут удовлетворять все точки, принадлежащие нижней полуплоскости и самой прямой 1.
Аналогичным образом отразим на графике решения неравенств (2)-(4).
Допустимое множество решений задачи линейного программирования находится в заштрихованной области и на ее границах.
Функционал (5) задачи строится аналогичным образом. Из всего допустимого множества (согласно теории математического программирования) представляют интерес только точки, расположенные в вершинах заштрихованной области:
А (0; 150); В (100; 100); С (400/3; 0); О (0; 0).
 |
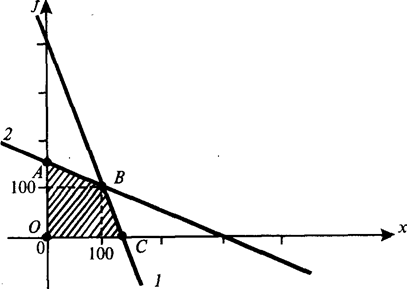Рис.1. Графический вариант решения модели (1)—(5):
1 — в соответствии с выражением (1);
2 — в соответствии с выражением (2).
Максимального значения, равного 90 000 ден.ед., функционал (5) достигает в вершине В, т.е. максимальный чистый дисконтированный доход, равный 90000 ден.ед., бизнесмен может получить, если приобретет 100 факсов и 100 ксероксов.
Итак, в качестве функционала нашей модели был рассмотрен некий простейший аналог критерия NРV, а в качестве значений правых частей ограничений модели использовались лимиты ресурсов проекта в денежном выражении. Неизвестными в данной задаче являлись стоимостные значения объемов проектных услуг.
На основании теории двойственности в математическом программировании можно построить задачу, двойственную данной, а полученные при ее решении так называемые двойственные переменные (объективно обусловленные оценки, теневые цены, скрытые цены, неявные цены) позволяют определить альтернативную стоимость используемых в проекте дефицитных ресурсов.
Построим задачу, двойственную нашей.
Пусть p1 — двойственная оценка фондов в первый год;
p2 — двойственная оценка фондов во второй год.
В этих обозначениях, необходимо минимизировать общие альтернативные стоимости совокупного объема фондов в целом за период проекта, т. е. минимизировать функцию
Z = (40 000 p1 + 30 000 p2 )
при следующих ограничениях:
100p1 + 200 p2 400;
300p1 + 100 p2 500;
Экономический смысл ограничений состоит в том, что продажа всех ресурсов (фондов), затрачиваемых на единицу каждого вида оборудования (факса или ксерокса) по их альтернативной стоимости в сумме не может быть меньше чистого дисконтированного дохода от одного факса или ксерокса (соответственно). Кроме того, альтернативные стоимости, как реальные экономические величины, не могут иметь отрицательных значений,поэтому: p1 0; p2 0;
Уже этот простой пример наглядно демонстрирует возможности и преимущества использования методов математического программирования для принятия проектных решений.
Экономико-математическая сущность анализа чувствительности состоит в следующем:
на основе базового варианта проекта определяют ожидаемое среднее отклонение каждой переменной величины (фактора) и результаты проекта в случае отклонения одной из переменных величин от базового сценария. Предполагают, что проект более чувствителен к изменению одного из параметров базового варианта, чем другого, если отклонение первого параметра дает большее отклонение критерия NРV — чистого дисконтированного дохода проекта (или другого критерия, выбранного для оценки) по сравнению с базовым сценарием.
Построим количественный показатель чувствительности проекта sens(у,хi ).Пусть у — некоторый критерий эффективности проекта. Он может быть функционально выражен через параметры проекта хi , т.е.
у = у(x1 ,x2 ,...,xk -1 , xk ).
В качестве показателя чувствительности проекта к изменению параметра х, рассчитаем отношение относительного приращения критерия к относительному приращению параметра:
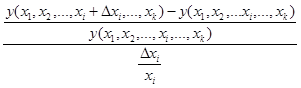
Однако при различных (дискретных) значениях 
будут получаться различные значения чувствительности. Чтобы этого не происходило, будем уменьшать так, чтобы в интервале 
функция у (хi
) при неизменных прочих х
приближалась к касательной в точке хi
,
тогда
Величина sens (у, хi ) показывает, на сколько процентов изменится значение критерия у проекта при изменении параметра хi на один процент.
Пример. Рассмотрим проект строительства нового завода по производству лазерных дисков.
Первоначально требуется вложить денежные средства в строительство завода и покупку технологии. Первоначальные затраты представляют собой фиксированное значение величины С0 , которая инвестируется сразу в момент времени t = 0.
Предположим, что ежемесячный выпуск будет постоянным и равным N лазерных дисков в месяц при постоянной же себестоимости Y, тогда ежемесячные издержки по выпуску равны NY. Пусть ежсмесячные постоянные издержки составят F. Производство лазерных дисков нaчнется через п месяцев после начала проекта.
Денежные поступления (выгоды) от проекта будут идти только в виде выручки от продажи продукции и цена Р одного лазерного диска постоянна во времени. Длительность проекта во времени не ограничена.
Чистый дисконтированный доход (NPV) проекта можно рассчитать на основании следующего уравнения:
, где r – ставка процента
Упростив формулу, получим:
| Числовые данные по проекту следующие: | |
| Первоначальные инвестиции С0 , долл. | 300 000 000 |
| Период первоначальных инвестиций п , мес. | 10 |
| Ежемесячный объем выпуска N, шт. | 200 000 |
| Цена единицы продукции Р, долл. | 1 600 |
| Переменные издержки на единицу продукции У, долл, | 1 000 |
| Фиксированные издержки за месяц F , долл. | 20 000 000 |
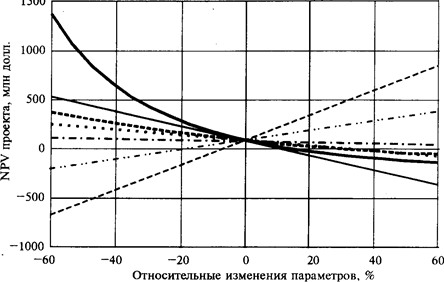
Рис.2. Чувствительность NPV к относительным изменениям параметров:
· · · · Со; - ·· - N ; ----- Р; —— У; —— r; -·- F; ----п
Базисное значение критерия чистого дисконтированного дохода
NPV0 = 85 543 289 долл.
Проведем анализ чувствительности, т.е. проанализируем реакцию изменений NPVна последовательные относительные изменения параметров проекта.
Показатели чувствительности NPV к изменению значений параметров имеют следующие значения:
| Параметр | r | Со | N | Р | У | F |
| Чувствигельность | -8,600 | -3,510 | 3,608 | 13,534 | -9,926 | 0,902 |
Кривые на графике (рис.2) пересекаются в точке, соответствующей рассчитанному ранее значению NPV0 . Очевидно, что в данной точке все параметры имеют нулевое отклонение (на рис.2 показано изменение NPV при сдвиге только одного из параметров).
Не всегда можно уверенно выбрать ставку процента (норму дисконта) для подсчета критерия NPV. Поэтому часто анализ чувствительности производится последовательно для наиболее вероятного, а также оптимистического и пессимистического сценариев (рис.3).
Так, например, если минимальная (оптимистический вариант) и максимальная (пессимистический вариант) ставки процента равны соответственно 6 и 16%, а наиболее вероятная — 10%, то, построив зависимости для NPV, получим семейства линий для каждого из параметров.
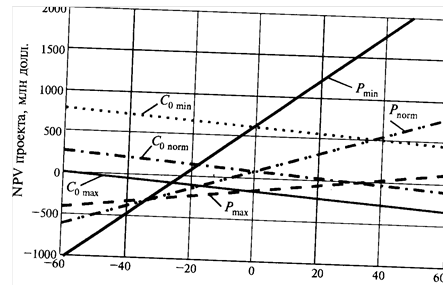
Рис.3. Зависимость NPV от начальных вложений и цены продукции при разных ставкахдисконтирования:
· · · · Соmin ; - · - Соnorm ; —— Соmax ;-··- Рnorm ;; —— Рmin ;----Рmax
Примечательно, что линии для Со параллельны друг другу, а линии для цены Р пересекаются в одной точке. Объяснение можно легко найти, проанализировав формулыNPV для данного проекта. Точка пересечения линий, показывающих чувствительность к цене (см.рис.3) — это та точка, в которой ежемесячные фиксированные издержки равны ежемесячному доходу, т.е. поток денежных средств состоит только из первоначальных инвестиций.
При анализе чувствительности расчетная задача часто ставится в следующем виде: каков предел негативных изменений данного параметра проекта, другими словами, на сколько пунктов может ухудшиться тот или иной параметр проекта, чтобы последний оставался прибыльным.
Анализ может быть сделан с использованием различных критериев эффективности (прибыльности) проекта. Однако результаты, полученные с помощью разных критериев, учитывающих временную ценность денег, т.е. дисконтирование, будут совпадать. Это легко понять, например: у проектов, где NPV = 0, равны между собой приведенные стоимости выгод (доходов) и затрат (издержек), отсюда — их отношение (В/С ratio ) равно единице. Аналогично индекс прибыльности, рссчитываемый как отношение дисконтированного потока доходов к дисконтированной сумме затрат, равен единице только тогда, когда NPV = 0. Напомним, что точка, в которой дисконтированные потоки выгод и затрат проекга равны между собой, была названа нами дисконтированной «точкой безубыточности».
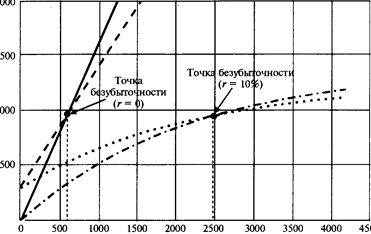Накопленный выпуск, тыс.штук.
Рис· 7.4. Поиск точки безубыточности:
—— накопленные доходы; --- накопленные издержки;
---- r = 0; -·- r = 10%
Она может быть найдена следующим образом (см.рис.4):
, где
где х — параметры проекта.
Для рассматриваемого проекта расчеты дают следующие значения
(при r= 10%):
| Без дисконтирования | С дисконтированием | |
| Объём выпуска, гарантирующий безубыточность, тыс.штук. | 600 | 2579,6 |
| Момент достижения точки беубыточности, мес. | 12 | 21,9 |
На основании изложенного выше можно рекомендовать следующую достаточно формализованную конкретную процедуру (примерную схему, формат) проведения анализа чувствительности инвестиционного проекта (табл.1-3):
Таблица 1
Формат: определения рейтинга факторов проекта, проверяемых на риск
| Переменная (фактор) | Изменение фактора | Новое значение | Изменение | Эластичность NPV | Рейтинг факторов пректа |
| х |  |
NPV |  NPV,% |
 |
|
| 1 | 2 | 3 | 4 | 5 | 6 |
Таблица 2
Показательчувствительности (важности) и прогнозируемости переменных в проекте
| Переменная | Эластичность NPV | Чувствительность (важность) | Возможность прогнозирования | Критическое значение |
| 1 | 2 | 3 | 4 | 5 |
| Чувствительность: | Высокая Средняя Низкая |
|||
| Возможность пргноза: | ||||
Высокая Средняя Низкая |
||||
Таблица 3
Матрица чувствительности и предсказуемости
| Предсказуемость переменных | Чувствительность переменной | ||
| Высокая | Средняя | Низкая | |
| Низкая | І | І | ІІ |
| Средняя | І | ІІ | ІІІ |
| Высокая | ІІ | ІІІ | ІІІ |
Примечание: І — дальнейшая проверка; ІІ — внимательно отслеживать; ІІІ — установить и забыть |
|||
Сделаем необходимые пояснения к предлагаемой схеме. Предположим, что в результате проведения качественного анализа были выявлены факторы проекта, проверяемые на риск (см. табл.1, графа 7), проведены расчеты базисного варианта проекта (в том числе определено, например, значение показателя NPV проекта, полностью удовлетворяющее всем необходимым требованиям) и выявлены граничные значения (в процентах) возможного изменения факторов (графа 2 — в данном случае представляют интерес изменения переменных, влекущие уменьшение эффективности проекга — рисковые). Графа 3 отражает последовательные расчеты новых значений NPV проекта, как результат изменений толъко одного фактора по отношению к его базисному значению. В графе 4 приведены расчеты процентных изменений NPV по отношению к ее базисному значению. Графа 5 — эластичность изменений NPV по отношению к изменению данного фактора. Графа 6 представляет собой ранжированную оценку — рейтинг факторов проекта на основе рассчитанного показателя эластичности NPV (при этом факторы нумеруются в порядке возрастания в зависимости от уменьшения показателей эластичности, таким образом, первым по рейтингу будет фактор с наибольшей эластичностью).
Перечень факторов проекта, включенных по степени убывания их рейтинговой оценки, и расчетные значения эластичностей NPV, приведенные в табл.1, отражены в графах 1,2 табл.2, которая в явной форме содержит экспертные оценки: деление факторов проекта по степени их чувствительности на три категории: более важную (входят факторы, к изменениям которых наиболее чувствителен показатель NPV, т.е. занимающие первые места в рейтинге), среднюю и низкую (см.графу 3); в графе 4 — экспертное распределение переменных проекта также на три категории (низкую, среднюю и высокую) по степени их прогнозируемости (т.е. возможности точного предвидения возможного изменения переменной); графа 5 — это расчет критического значения каждой переменной проекта, т.е. такого, при котором значение критерия NPV проекга становится равным нулю (или, по нашему определению, рассчитывается критическое значение фактора, соответствующее дисконтированной точке безубыточности проекта).
Матрица чувствительности (см. табл.3), степени которой отражены в сказуемом таблицы — по горизонтали и важности, степени которой представлены в подлежащем — по вертикали. На основе результатов работы с табл.3 каждый фактор занимает соответствующее место в поле матрицы (табл.3). В соответствии с экспертным разбиением чувствительности и предсказуемости по их степеням матрица содержит девять элементов, которые можно распределитъ по зонам. Попадание фактора в определенную зону означает конкретную рекомендацию для принятия решения о дальнейшей работе по анализу его риска. Итак, первоя зона — левый верхний угол матрицы — зона дальнейшего анализа попавших в нее факторов, так как к их изменению наиболее чувствительна NPV проекта, и они обладают наименьшей прогаозируемостью. Вторая зона совпадает с элементами главной диагонали матрицы и требует пристального внимания к происходящим изменениям расположенных в ней факторов (в частности, в том числе и для этого производился расчет критических значений каждого фактора). Наконец, третья зона — зона наибольшего благополучия: те факторы, которые при всех прочих сделанных нами предположениях и расчетах попали в правый нижний угол таблицы, являются наименее рискованными и не подлежат дальнейшему рассмотрению.
Отметим, что несмотря на все преимущества метода анализа чувствительности: объективность, теоретическую прозрачность, простоту расчетов, экономико-математическую естественность результатов и наглядность их толкования (именно эти критерии лежат в основе его широкого практического использования) — метод обладает и существенными недостатками, основным из которых является его однофакторность, т.е. ориентированность на изменения только одного фактора проекта, что приводит к недоучету возможной связи между отдельными факторами или недоучету их корреляции.
Список использованной литературы
1. Баренс В., Хавренек П. М. Руководство по оценке эффективности инвестиций: Пер. с англ.- М.: АОЗТ «Интерэксперт», 1995. - 528 с.
2. Бирман Г., Шмидт С. Экономический анализ инвестиционных проектов: Пер. с англ. / Под ред. Л.П. Белыx. - М.: Банки и биржи, ЮНИТИ,1997.-631с.
3. Бланк И. А. Инвестиционрый менеджмент. - К.: МП «ИТЕМ» ЛТД,
4. 1995.-448с.
5. Волков Н. Г. Учет долгосрочных инвестиций и источников их финансирования. -М.: Финансы и статистика, 1998. ;
6. Волков И. М., Грачева М.В. Проектный анализ. - М.: Банки и биржи, ЮНИТИ, 1998. - 423 с.
7. Ковалев В.В. Финансовый анализ: Управление капиталом. Выбор инвестиций. Анализ отчетности. -М.: Финансы и статистика, 1996.-432с.
8. Ковалев В. В. Методы оценки инвестиционных проектов, - М.:
9. Финансы и статистика, 1998. - 144 с.
10. Мелкумов Я.С.Экономическая оценка эффективности инвестиций.- М.: ИКЦ «ДИС», 1997. - 160 с.
11. Управление инвестициями/Под ред. В.В.Шеремета. В 2-х т.- М.: Высшая школа, 1998.