Вектор

СОДЕРЖАНИЕ: Уральский Государственный Колледж Имени И.И.Ползунова Доклад на тему: «Векторы» Выполнил:Ланглиц.А.И Группа: Б-147 Преподаватель:Запорожан.В.В

Уральский Государственный Колледж Имени И.И.Ползунова

Доклад на тему:

«Векторы»

Выполнил:Ланглиц.А.И

Группа: Б-147

Преподаватель:Запорожан.В.В

Екатеринбург 2010

СОДЕРЖАНИЕ

Глава 1. Понятие вектора.

Глава 2. Простейшие операции над векторами.

Глава 3. Линейная зависимость векторов.

Глава 4. Понятие базиса. Координаты вектора в данном базисе.

Глава 5. Проекция вектора.

Глава 6. Скалярное произведение.

Глава 7. Векторное произведение.

Глава 8. Смешанное произведение.

Литература

Глава 1. Понятие вектора
Отрезок на прямой определяется двумя равноправными точками – его концами. Различают также направленный отрезок, т.е. отрезок, относительно концов которого известно какой из них первый (начало), а какой – второй (конец).

Определение: Направленный отрезок (или упорядоченная пара точек) называетсявектором .

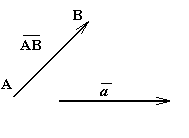
Вектор обычно обозначается символом , где А – начало, а В – конец направленного отрезка, либо одной буквой (в некоторых учебниках буква выделяется полужирным шрифтом; при этом стрелка опускается a ). На чертеже вектор изображается стрелкой. Начало вектора называют точкой его приложения .

Расстояние между началом и концом вектора называется его длиной. Для обозначения длины вектора (его абсолютной величины) пользуются символом модуля. Так и обозначают длины соответствующих векторов.

Вектор единичной длины называют ортом .

К векторам будем относить и так называемый нулевой вектор , у которого начало и конец совпадают. Считается, что нулевой вектор не имеет определенного направления и имеет длину равную нулю. Это позволяет обозначать нулевой вектор вещественным числом 0 (нуль).

Векторы расположенные либо на одной прямой, либо на параллельных прямых называются коллинеарными . Нулевой вектор считается коллинеарным любому вектору. Среди коллениарных векторов различают одинаково направленные (сонаправленные) и противоположно направленные векторы.

Векторы называются компланарными , если они лежат либо на одной плоскости, либо на прямых, параллельных одной и той же плоскости.

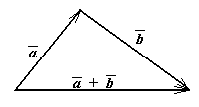
Определение: Два вектора называются равными , если они: 1) коллинеарны; 2) равны по длине; 3) одинаково направлены.

Следствие: Для любого вектора и для любой точки А, существует, и притом единственная, точка B такая, что .

Мы не будем различать двух равных векторов, имеющих разные точки приложения. Такие векторы называются свободными (в отличие от скользящих и связанных векторов, встречающихся в других науках).

Понятие равенства векторов обладает следующими свойствами:

1. (рефлексивность).

2. Из того, что , следует (симметричность).

3. Из того, что и , следует (транзитивность).

Глава 2. Операции над векторами

Определение: Суммой двух векторов и называется вектор, имеющий начало в начале вектора , а конец – в конце вектора , при условии, что вектор приложен к концу вектора .

В соответствии с определением слагаемые и и их сумма образуют треугольник (рис.2). Поэтому данное правило сложения двух векторов называют «правилом треугольника».

Операция сложения векторов обладает свойствами:

1. (коммутативность);

2. , (ассоциативность);

3. для любого вектора (особая роль нулевого вектора);

4. для каждого вектора существует противоположный ему вектор такой, что (для получения достаточно поменять местами начало и конец вектора ).

Вектор противоположный вектору обозначают .

Определение: Разностью векторов и называется сумма вектора и вектора противоположного вектору , т.е. .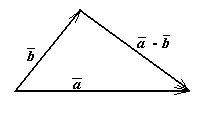

Разность получается из вектора сдвигом его начала в конец вектора , при условии, что векторы и имеют общее начало (рис.3). Очевидно, что для любого вектора .

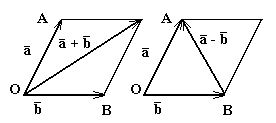
Замечание: Существует еще одно правило сложения векторов, называемое «правилом параллелограмма»: векторы и прикладываются к общему началу О , и на них строится параллелограмм (рис. 4). Суммой будет вектор , расположенный на диагонали параллелограмма. Разностью здесь будет вектор , расположенный на второй диагонали.

Векторная алгебра имеет дело с двумя типами величин: векторами и числами. Числа обычно называют скалярными величинами или скалярами .

Определение: Произведением вектора на вещественное число (скаляр) называется вектор , такой, что 1) ; 2) вектор коллинеарен вектору ; 3) векторы и имеют одинаковое (противоположное) направление если 0 ( 0).

Замечание: В случае, когда = 0 или произведение является нулевым вектором.

Операция умножения вектора на число обладает следующими свойствами:

1. (ассоциативное свойство сомножителей);

Действительно, заметим, что векторы, стоящие обеих частях равенства, имеют одну и ту же длину . Кроме того, они коллинеарны и одинаково направлены, так как их направление совпадает с направлением , если и одного знака, и противоположно направлению , если и имеют разные знаки. Если же или равны нулю, то обе части равенства равны нулю. Свойство доказано.

2. 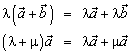(свойства дистрибутивности).

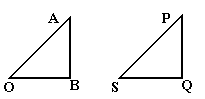
Построим треугольник OAB где и . Построим далее треугольник SPQ , где и . Так как стороны SP , PQ треугольника SPQ параллельны и пропорциональны сторонам OA , AB треугольника OAB , то эти треугольники подобны. Поэтому сторона SQ также параллельна стороне OB и отношение их длин также равно ||. Ясно, далее, что и одинаково направлены, если 0. Отсюда следует, что . Но и , а отсюда вытекает первое свойство дистрибутивности.

Очевидно, что векторы стоящие в обеих частях второго свойства дистрибутивности коллинеарны. Допустим сначала, что знаки и одинаковы. Тогда векторы и направлены одинаково и длина их суммы равна сумме их длин, т. е. . Но и следовательно, в этом случае векторы и равны по длине. Направление их совпадает с направлением вектора , если общий знак и положителен, и противоположно ему, если отрицателен. Допустим теперь, что знаки и различны, и для определенности будем считать || ||. В этом случае длина суммы равна разности длин, точнее . Но . Следовательно, и в этом случае длина вектора равна длине вектора . Очевидно, что оба эти вектора направлены так же, как . Если же || = || и знаки и противоположны, то обе части равенства равны нулю. То же обстоятельство имеет место, если равен нулю вектор или оба скаляра одновременно.

Теорема: Если вектор коллинеарен ненулевому вектору , то существует вещественное число такое, что = .

Глава 3. Линейная зависимость векторов

Любое множество, элементами которого являются векторы, называется системой векторов . Выражение вида , где _i – вещественное число, называется линейной комбинацией векторов системы . Числа _i называются коэффициентами линейной комбинации. Различают два типа линейных комбинаций: тривиальные , когда и нетривиальные .

Если , то говорят, что вектор представлен (разложен) в виде линейной комбинации векторов системы . Разумеется, нулевой вектор может быть представлен в виде тривиальной линейной комбинации любой системы векторов. Тривиальная линейная комбинация любой системы векторов равна нулю.

Определение: Система векторов называется линейно зависимой , если хотя бы одна нетривиальная линейная комбинация векторов системы обращается в нуль, т.е. имеет место равенство , при .

Система векторов не являющаяся линейно зависимой называется линейно независимой .

Определение: Система векторов называется линейно независимой , если равенство нулю линейной комбинации векторов системы возможно лишь в случае ее тривиальности, т.е. из того, что следует .

Теорема: Если хотя бы один из векторов системы является нулевым, то эта система является линейно зависимой.

Действительно, из векторов системы можно составить линейную комбинацию , которая не является тривиальной.

Теорема: Если часть системы векторов линейно зависима то и вся система векторов линейно зависима.

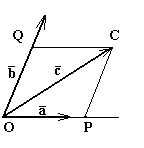
Действительно, если система векторов линейно зависима, то существует нетривиальная линейная комбинация . Для любой системы векторов линейная комбинация также является нетривиальной.

Теорема: Необходимым и достаточным условием линейной зависимости двух векторов является их коллинеарность.

Действительно, либо оба коллинеарных вектора равны нулю, и тогда равна нулю любая их линейная комбинация (в том числе и нетривиальная), либо один из них не нуль, и тогда, в силу теоремы из второго раздела, другой отличается от него на числовой множитель. Запишем это: . Но эта же запись означает, что , и мы имеем нетривиальную линейную комбинацию, равную нулю.

Наоборот, допустим, что два неколлинеарных вектора и линейно зависимы. Тогда существуют коэффициенты и такие, что , причем, например, 0. Это означает, что , и векторы коллинеарны, вопреки нашему предположению.

Следствие: Если два вектора неколлинеарны, то они линейно независимы.

Теорема: Любой вектор лежащий в одной плоскости с неколлинеарными векторами и , может быть представлен в виде линейной комбинации этих векторов (т.е. найдутся такие вещественные числа и , что ). Такое представление единственно.

Заметим, прежде всего, что оба вектора и отличны от нуля, так как если бы хоть один из них был нулевым, то они были бы коллинеарны. Если вектор коллинеарен одному из данных векторов, то утверждение сводится к теореме из второго раздела.

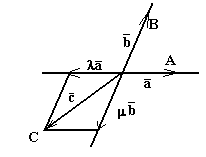
В общем случае перенесем все три вектора в одну точку О (рис. 6). Через конец C вектора проведем прямые CР и CQ , параллельные векторам и . Тогда , причем векторы и коллинеарны соответственно и . В силу теоремы из второго раздела существуют и определены однозначно такие числа и , что , . Таким образом, , что и требовалось.

Допустим теперь, что существует другая линейная комбинация , равная , причем, например . Тогда , так как иначе мы имели бы две прямые, проходящие через точку C параллельно вектору . Из последнего равенства вытекает, что = , в противоречие с нашим предположением.

Следствие: Необходимым и достаточным условием линейной зависимости трех векторов является их компланарность.

В самом деле, пусть векторы , , линейно зависимы, тогда один из них есть линейная комбинация двух других. Пусть, например . Приложим векторы , , к одной и той же точке О (рис. 7), так что , , .

Предположим сначала, что векторы , не коллинеарны; тогда несущие их прямые определяют некоторую плоскость. В этой плоскости лежат и векторы и , а значит, и весь параллелограмм, на этих векторах построенный, в частности и его диагональ . Значит все три вектора , , компланарны.

Если векторы и коллинеарны, то коллинеарны как векторы , , так и их сумма - три вектора , , оказываются даже коллинеарными.

Если же векторы , , компланарны, то либо один из них, например , лежит в одной плоскости с двумя другими неколлинеарными векторами (следовательно ; или ), либо все три вектора коллинеарны (следовательно ). Тем самым следствие полностью доказано.

Следствие: Если три вектора некомпланарны, то они линейно независимы.

Теорема: Любой вектор может быть представлен в виде линейной комбинации трех некомпланарных векторов , и (т.е. найдутся такие числа , , , что ). Такое представление единственно.

Никакие два из векторов , и не коллинеарны, иначе все три были бы компланарны. Поэтому, если компланарен с какими-нибудь двумя из данных векторов, то наше утверждение вытекает из предыдущего следствия.

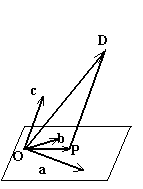
В общем случае перенесем все векторы в одну точку О (рис. 8) и проведем через конец D вектора прямую, параллельную вектору . Она пересечет плоскость ОЕ₁ Е₂ в точке Р . Очевидно, что . Согласно теореме из второго раздела и предыдущему следствию существуют такие числа , и , что и . Таким образом, .

Единственность коэффициентов линейной комбинации доказывается так же, как и предыдущем следствии.

Следствие: Любые четыре вектора линейно зависимы

Глава 4. Понятие базиса. Свойства вектора в данном базисе

Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов.

Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.

Базис в пространстве позволяет однозначно сопоставить каждому вектору упорядоченную тройку чисел – коэффициенты представления этого вектора в виде линейной комбинации векторов базиса. Наоборот, каждой упорядоченной тройке чисел при помощи базиса мы сопоставим вектор , если составим линейную комбинацию .

Числа – называются компонентами (или координатами ) вектора в данном базисе (записывается ).

Теорема: При сложении двух векторов их координаты складываются. При умножении вектора на число все координаты вектора умножаются на это число.

Действительно, если и , то

.

Определение и свойства координат вектора на плоскости аналогичны. Вы легко можете сформулировать их самостоятельно.

Глава 5. Проекция вектора

Под углом между векторами понимается угол между векторами равными данным и имеющими общее начало. Если направление отсчета угла не указано, то углом между векторами считается тот из углов, который не превосходит . Если один из векторов нулевой то угол считается равным нулю. Если угол между векторами прямой то векторы называются ортогональными .

Определение: Ортогональной проекцией вектора на направление вектора называется скалярная величина , – угол между векторами (рис.9).

Модуль этой скалярной величины равен длине отрезка OA₀ .

Если угол острый проекция является положительной величиной, если угол тупой – проекция отрицательна, если угол прямой – проекция равна нулю.

При ортогональной проекции угол между отрезками OA₀ и AA₀ прямой. Существуют проекции, у которых этот угол отличен от прямого.

Проекции векторов обладают следующими свойствами:

1. (проекция суммы равна сумме проекций);

2. (проекция произведения вектора на число равна произведению проекции вектора на число).

Базис называется ортогональным , если его векторы попарно ортогональны.

Ортогональный базис называется ортонормированным , если его векторы по длине равны единице. Для ортонормированного базиса в пространстве часто используют обозначения .

Теорема: В ортонормированном базисе координаты векторов есть соответствующие ортогональные проекции этого вектора на направления координатных векторов.

Пример: Пусть вектор единичной длины образует с вектором ортонормированного базиса на плоскости угол , тогда .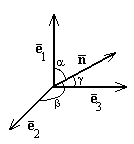

Пример: Пусть вектор единичной длины образует с векторами , и ортонормированного базиса в пространстве углы , , , соответственно (рис.11), тогда . Причем . Величины cos, cos, cos называются направляющими косинусами вектора

Глава 6. Скалярное произведение

Определение: Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Если один из векторов нулевой скалярное произведение считается равным нулю.

Скалярное произведение векторов и обозначается через [или ; или ]. Если - угол между векторами и , то .

Скалярное произведение обладает следующими свойствами:

1. (коммутативность).

2. (скалярный квадрат вектора равен квадрату его длины).

3. Скалярное произведение равно нулю тогда и только тогда, когда сомножители ортогональны или хотя бы один из них нулевой.

4. .

5. .

6. .

Теорема: В ортогональном базисе компоненты любого вектора находятся по формулам:

; ; .

Действительно, пусть , причем каждое слагаемое коллинеарно соответствующему базисному вектору. Из теоремы второго раздела следует, что , где выбирается знак плюс или минус в зависимости от того, одинаково или противоположно направлены векторы , и . Но, , где - угол между векторами , и . Итак, . Аналогично вычисляются и остальные компоненты.

Скалярное произведение используется для решения следующих основных задач:

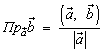1. ; 2. ; 3. .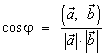

Пусть в некотором базисе заданы векторы и тогда, пользуясь свойствами скалярного произведения, можно записать:

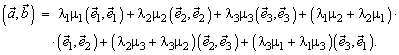
Величины называются метрическими коэффициентами данного базиса. Следовательно .

Теорема: В ортонормированном базисе

;
;
;
.

Замечание: Все рассуждения этого раздела приведены для случая расположения векторов в пространстве. Случай расположения векторов на плоскости получается изъятием лишних компонент. Автор предлагает сделать вам это самостоятельно.

Глава 7. Векторное произведение

Упорядоченная тройка некомпланарных векторов называется правоориентированной (правой ), если после приложения к общему началу из конца третьего вектора кратчайший поворот от первого вектора ко второму виден против часовой стрелки. В противном случае упорядоченная тройка некомпланарных векторов называется левоориентированной (левой ).

Определение: Векторным произведением вектора на вектор называется вектор , удовлетворяющий условиям:

1. где – угол между векторами и ;

2. вектор ортогонален вектору , вектор ортогонален вектору ;

3. упорядоченная тройка векторов является правой.

Если один из векторов нулевой, то векторное произведение есть нулевой вектор.

Векторное произведение вектора на вектор обозначается {либо }.

Теорема: Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.

Теорема: Длина (модуль) векторного произведения двух векторов равняется площади параллелограмма, построенного на этих векторах как на сторонах.

Пример: Если – правый ортонормированный базис, то , , .

Пример: Если – левый ортонормированный базис, то , , .

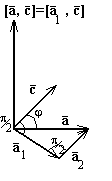
Пример: Пусть, а ортогонален к . Тогда получается из вектора поворотом вокруг вектора на по часовой стрелке (если смотреть из конца вектора ).

Пример: Если дан вектор , то каждый вектор можно представить в виде суммы , где – ортогонален , а – коллинеарен . Легко видеть, что .

Действительно, можно заметить, что . Вектор компланарен векторам и , а потому и коллинеарны. Легко видеть (рис. 12), что они одинаково направлены.

Векторное произведение обладает следующими свойствами:

1. (антикоммутативность);

Действительно, из определения следует, что модуль векторного произведения не зависит от порядка сомножителей. Точно так же вектор коллинеарен вектору . Однако, переставляя сомножители, мы должны изменить направление произведения, чтобы было выполнено условие 3) определения. Действительно, если , , - правая тройка, то , , - левая, а , , - снова правая тройка.

2. ;

Если - угол между векторами и , то . Векторы, стоящие в обеих частях доказываемого равенства, лежат на прямой, перпендикулярной и . При 0 и вектор и вектор направлены так же, как . Если 0, то кратчайший поворот от к производится навстречу кратчайшему повороту от к . Поэтому и противоположно направлены. Очевидно, что противоположно направлены также и векторы и . Таким образом, при 0 векторы и направлены всегда одинаково, и равенство доказано. При = 0 равенство очевидно.

3. ;

Если , то доказываемое очевидно. Если , то разложим и в суммы и , где и ортогональны , а и коллинеарны . Поскольку , и вектор ортогонален , а коллинеарен , нам достаточно доказать равенство и (в силу свойства 2) даже равенство , где . Длина вектора равна 1. Выше, в примере, мы видели, что в этом случае умножение на сводится к повороту (ортогонального к ) первого сомножителя на угол 90°. Но при повороте параллелограмм, построенный на и , поворачивается целиком вместе с диагональю. Тем самым равенство доказано.

4. .

Пусть в некотором базисе заданы векторы и тогда

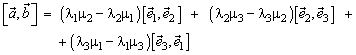
или

Теорема: В ортонормированном базисе

или

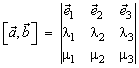
{если базис левый, то перед одной из частей каждого равенства следует поставить знак минус}.

Справедливость теоремы следует из предыдущих формул при учете примеров в начале раздела. Чтобы избежать постоянных замечаний об ориентации базиса, мы будем считать, что базис выбирается всегда правый.

Векторное произведение используется в основном для решения двух задач:

1. Нахождения вектора перпендикулярного плоскости, в которой расположены два заданных вектора.

2. 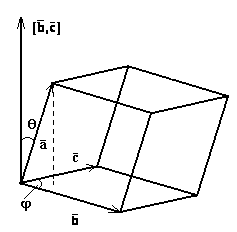Вычисление площади S параллелограмма, построенного на векторах и , как на сторонах. В ортонормированном базисе

.

В планиметрии векторное произведение не определено. Но ничто не мешает считать, что изучаемая плоскость помещена в пространство и третий базисный вектор выбран единичным и перпендикулярным плоскости. Тогда векторное произведение имеет одну ненулевую компоненту, а именно третью, и площадь параллелограмма в ортонормированном базисе на плоскости выражается формулой

.

Глава 8. Смешанное произведение

Определение: число называется смешанным произведением векторов , и .

Смешанное произведение векторов , и обозначается или .

Теорема: Смешанное произведение трех векторов равно объему параллелепипеда, построенного на векторах как на ребрах, взятому со знаком плюс если тройка правая, и со знаком минус, если тройка левая.

Действительно, , где - угол между векторами и , а - угол между векторами и . Объем параллелепипеда, построенного на векторах , и , равен (рис. 13) произведению площади основания на высоту . Таким образом, первое утверждение доказано. Знак смешанного произведения совпадает со знаком cos, и поэтому смешанное произведение положительно когда направлен в ту же сторону от плоскости векторов и , что и вектор , т. е. когда тройка , , правая. Аналогично доказывается, что смешанное произведение левой тройки векторов отрицательно.

Пример: Если - ортонормированный базис, то или , смотря по тому, правый это базис или левый.

Теорема: Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.

Равенство возможно в следующих случаях:

a.хотя бы один вектор нулевой; тогда все три вектоpaкомпланарны;

b.sin = 0 тогда и коллинеарны, и следовательно , и компланарны;

c.cos = 0 тогда вектор ортогонален , т. е. компланарен и .

Обратное утверждение доказывается аналогично.

Смешанное произведение обладает следующими свойствами:

1. ;

2. ;

3. .

Пусть в некотором базисе векторы , , , тогда

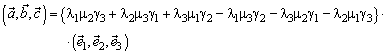
или

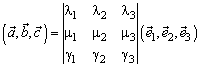
В частности, в ортонормированном базисе

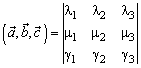
{если базис левый, то перед одной из частей равенства следует поставить знак минус}.

Следствие: Условие

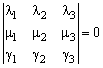
является необходимым и достаточным условием компланарности трех векторов, заданных своими координатами в некотором базисе

Литература

• Александров П.С. Лекции по аналитической геометрии. М, Наука, 1968, 912 с.
• Мусхелишвили Н.И. Курс аналитической геометрии. М, Высшая школа, 1967, 655 с.
• Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М, Наука, 1971, 328 с.

Действительно, этим числом является или , или в зависимости от того, направлены ли векторы и одинаково или противоположно. Если , то = 0. Единственность множителя очевидна: при умножении на разные числа мы получим различные векторы.

Скачать архив с текстом документа