Векторный метод решения стереометрических задач
СОДЕРЖАНИЕ: Векторный метод решения стереометрических задач Задача 1. Отрезок, соединяющий вершину тетраэдра с центроидом противолежащей грани, называется медианой этого тетраэдра; отрезок, соединяющий середины противоположных ребер тетраэдра, называется его бимедианой. Докажите:Векторный метод решения стереометрических задач
Задача 1. Отрезок, соединяющий вершину тетраэдра с центроидом противолежащей грани, называется медианой этого тетраэдра; отрезок, соединяющий середины противоположных ребер тетраэдра, называется его бимедианой. Докажите:
а) что все медианы тетраэдра пересекаются в одной точке и эта точка делит каждую из медиан в отношении 3:1, считая от вершины;
б) все бимедианы тетраэдра пересекаются в одной точке и делятся ею пополам;
в) точка пересечения бимедиан тетраэдра совпадает с точкой пересечения его медиан.
Решение.
а) Пусть Н1 , Н2 , Н3 , Н4 — центроиды граней соответственно АВС, АВР, ВСР, АСР; М — точка, делящая медиану РН1 тетраэдра РАВС в отношении РМ : МН1 = 3 : 1( рис. 1).
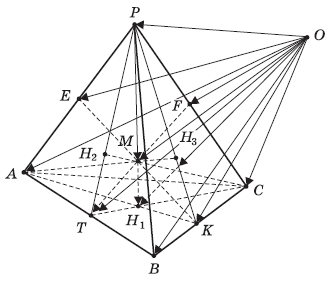
Рис. 1
Тогда РМ : РН1
= 3 : 4, откуда 
Для любой точки О пространства и центроида Н1
грани АВС выполняется равенство:
Тогда
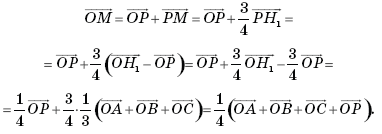
Аналогично можно доказать, что для точек М1 , М2 и М3 , делящих медианы соответственно СН2 , АН3 , ВН4 тетраэдра в отношении 3 : 1, считая соответственно от вершин С, А и В, выполняется то же равенство, то есть
Это означает, что точки М, М1 , М2 и М3 совпадают, то есть все четыре медианы РН1 , СН2 , АН3 и ВН4 тетраэдра пересекаются в одной точке М и делятся этой точкой в отношении 3 : 1, считая от соответствующей вершины, что и требовалось доказать.
Точка пересечения медиан тетраэдра называется центроидом этого тетраэдра.
б) Пусть точки K и Е — середины ребер соответственно ВС и АР (см. рис. 1), то есть отрезок KЕ — бимедиана тетраэдра РАВС. Если точка Q — середина бимедианы KЕ, то для любой точки О пространства выполняется:
Так как K и Е — середины ребер соответственно ВС и АР, то справедливы равенства:
Тогда получаем:
Аналогично можно доказать, что для середины Q1
бимедианы ТF (см. рис.1) имеет место: 
Можно убедиться, что такое же равенство выполняется и для середины Q2
третьей бимедианы данного тетраэдра. Это означает: 
откуда следует, что точки Q, Q1
и Q2
совпадают, то есть все три бимедианы тетраэдра пересекаются в одной точке Q и делятся этой точкой пополам.
в) Таким образом, для точек М и Q справедливы соответственно равенства:
и
из которых следует, что 
откуда: точка Q пересечения бимедиан тетраэдра РАВС совпадает с его центроидом М, что и требовалось доказать.
Условие компланарности трех векторов
В качестве базиса в пространстве можно выбрать любую упорядоченную тройку некомпланарных векторов 
Тогда любой вектор 
пространства единственным образом можно разложить по векторам этого базиса: 
В общем виде критерий компланарности трех ненулевых векторов 
выражает равенство: 
(при условии, что не все коэффициенты одновременно равны нулю). Если в задаче требуется доказать, что три данные прямые параллельны некоторой плоскости (ее положение определять не нужно), то достаточно на каждой из этих прямых выбрать вектор и, используя признак компланарности трех векторов, доказать, что выбранные векторы компланарны.
Задача 2.В параллелепипеде АВСDА1 В1 С1 D1 точка М— середина диагонали А1 С1 грани A1 B1 C1 D1 , точка K— середина ребра ВВ1 . Докажите, что прямые А1 В1 , KМ и ВС1 параллельны некоторой плоскости.
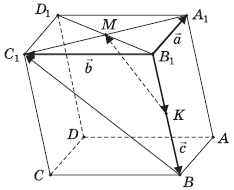
Рис. 2
Решение.
Введем векторы: 
(рис.2).
Тройку 
некомпланарных векторов 
примем в качестве базиса. Разложим векторы 
по векторам этого базиса.
Имеем: 
Тогда
Это означает, что векторы 
компланарны, следовательно, они параллельны некоторой плоскости, тогда этой плоскости параллельны и прямые А1
В1
, KМ и ВС1
, для которых векторы 
являются направляющими.
Задача 3. На диагоналях АВ1 и ВС1 граней AA1 B1 B и ВВ1 С1 С параллелепипеда ABCDA1 B1 C1 D1 взяты точки соответственно Н и M так, что отрезки MН и A1 C параллельны. Найдите отношение длин этих отрезков.
Решение.
Введем векторы:
(рис.3).
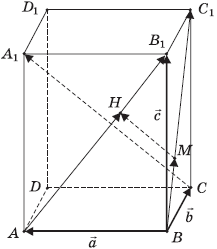
Рис. 3
Тройку 
некомпланарных векторов 
примем в качестве базиса и разложим векторы 
по векторам этого базиса. Имеем:
Так как точка Н лежит на диагонали АВ1
, то векторы 
коллинеарны, поэтому существует такое число х, что 
Аналогично, в силу коллинеарности векторов 
существует такое число у, что 
По правилу ломаной находим:
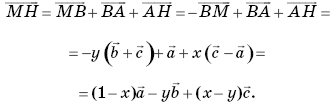
По условию MН 
A1
C, значит, существует такое число t, что 
то есть выполняется равенство:
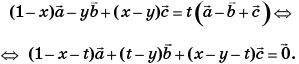
Вследствие некомпланарности векторов 
и единственности разложения вектора по базису, приходим к выводу: 1 – х – t = 0, t – у = 0, х – у – t = 0. Решением этой системы уравнений является: 
Тогда 
значит, МН : СА1
= 1 : 3.
Ответ: 1 : 3.