Изучение затухающих электромагнитных колебаний 2
СОДЕРЖАНИЕ: Введение Целью данной работы является изучение работы колебательного контура, свободных затухающих колебаний и их характеристик. 1. Описание экспериментальной установки и методики измерений.Введение
Целью данной работы является изучение работы колебательного контура, свободных затухающих колебаний и их характеристик.
1. Описание экспериментальной установки и методики измерений.
Схема установки представлена на рисунке 1.1. Колебания в контуре II возбуждаются с помощью генератора импульсного напряжения, вырабатываемого в контуре I, собранного на резисторе R1, емкости C1 и диоде VD1.
|
|

Рисунок 1.1-Схема экспериментальной установки.
Схема смонтирована на съемной панели лабораторного макета. В качестве резистора в RP1 в колебательном контуре II используется переменное сопротивление, максимальное значение которого находится в зависимости от номера съемной панели (470 Ом , 680 Ом и др.) и устанавливается поворотом ручки потенциометра по часовой стрелке в крайнее положение. При повороте ручки против часовой стрелки в крайнее положение значение сопротивления RP1 =0. В этом случае активное сопротивление колебательного контура складывается из сопротивления соединительных проводов контура и активного сопротивления катушки индуктивности, R=Rx . В дальнейшем это сопротивление необходимо рассчитать по результатам измерений.
Возбуждение контура производится периодически от генератора импульсного напряжения I, регистрируются колебания на осциллографе III. Каждый импульс, подаваемый с генератора на колебательный контур, возбуждает один цуг затухающих колебаний.
Измерения амплитуды и периода колебаний осуществляется непосредственно с помощью осциллографа.
2. Основные расчетные формулы.
![]() (2.1)
(2.1)
где n – логарифмический декремент затухания
Un – амплитуда напряжения n-того колебания
Un +1 – амплитуда напряжения (n+1) колебания
![]() (2.2)
(2.2)
где L – индуктивность контура
RP 1 – сопротивление нагрузки (RP1=352,5 Ом)
1 – коэффициент затухания в первом случае
2 – коэффициент затухания во втором случае
![]() (2.3)
(2.3)
где Rx – сопротивление контура
L – индуктивность контура
1 – коэффициент затухания в первом случае
![]() (2.4)
(2.4)
где 0 – собственная частота контура
L – индуктивность контура
С – ёмкость конденсатора (С=0,047 мкФ)
![]() (2.5)
(2.5)
где – частота затухающих колебаний
0 – собственная частота контура
– коэффициент затухания
![]() (2.6)
(2.6)
где T – период затухающих колебаний
– частота затухающих колебаний
![]() (2.7)
(2.7)
где R кр – критическое сопротивление
L – индуктивность контура
С – ёмкость конденсатора (С=0,047 мкФ)
![]() (2.8)
(2.8)
где Q – добротность контура
– логарифмический декремент затухания
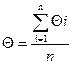 (2.9)
(2.9)
где n – количество суммированных значений
3. Результаты работы и их анализ.
Таблица 3.1
Значение активного сопротивления R |
Номер измеряемой амплитуды n |
Значение амплитуды Un , дел. |
Значение логарифмического декремента затухания
|
Среднее значение
|
Период колебаний T, с. |
|
R= Rx |
1 2 3 4 5 |
5 3,3 2,2 1,4 0,9 |
0,416 0,405 0,452 0,442 |
0,492 |
0 0,416 0,821 1,273 1,715 |
10-3 с |
R= Rx + RP1 |
1 2 3 4 5 |
4 1,8 0,8 0,4 0,2 |
0,799 0,811 0,693 0,693 |
0,749 |
0 0,799 1,609 2,303 2,996 |
10-3 с |
Рассчитаем значения логарифмических декрементов по формуле (2.1):
![]()
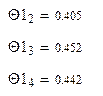
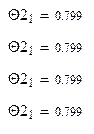
Вычислим средние значения логарифмического декремента в обоих случаях по формуле (2.9):
![]()
![]()
Построим графики зависимостей ![]() для обоих случаев:
для обоих случаев:
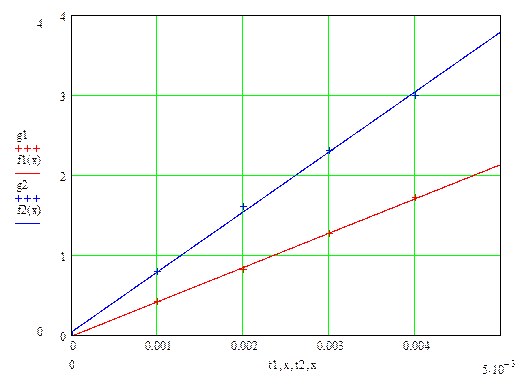
Рисунок 3.1
Найдём значение коэффициентов затухания, это угловые коэффициенты прямых:
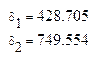
Определим величину индуктивности контура по формуле (2.2)
![]()
Рассчитаем суммарное активное сопротивление по формуле (2.3):
![]()
Найдём собственную частоту контура по формуле (2.4):
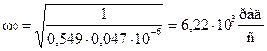
Вычислим частоты затухающих колебаний по формуле (2.5):
![]()
![]()
Определим периоды по формуле (2.6):
![]()
![]()
Найдём значение критического напряжения по формуле (2.7):
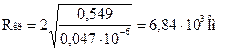
Определим добротность контура в обоих случаях по формуле (2.8):
![]()
![]()
Заключение
В ходе выполнения данной лабораторной работы была изучена работа колебательного контура и основные характеристики свободных затухающих колебаний. Проверена справедливость экспоненциального закона убывания амплитуды со временем, что подтверждает зависимость ![]() представленная на рисунке 3.1.
представленная на рисунке 3.1.