Изучение зрительной трубы

СОДЕРЖАНИЕ: Определение увеличения зрительной трубы. Определение поля зрения оптической трубы. Определение разрешающей способности оптических систем. Предел разрешения. Определение предела разрешения глаза, систем зрительная труба – глаз.

Лабораторная работа № 3

Изучение зрительной трубы

Упражнение 1

Определение увеличения зрительной трубы

В этой задаче увеличение зрительной трубы определяется двумя методами.

Первый метод . Пусть –предмет, находящийся на расстоянии от глаза наблюдателя, - изображение предмета, видимое в трубу и находящееся на расстоянии от , и –соответствующие углы зрения (рис.1).

Рис. 1 .

Согласно определению увеличение

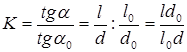Спроектируем изображение на плоскость предмета при помощи центральной проекции с центром в точке , то есть так, чтобы все точки изображения переместились вдоль лучей, соединяющих их с глазом наблюдателя. Спроектированное таким образом изображение займет положение . Очевидно, что угол зрения, под которым видна эта проекция, есть , а расстояние её от глаза есть . В этом случае увеличение:

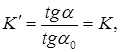то есть .

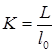Если предмет представляет собой шкалу, длина одного деления которой есть , то, спроектировав её изображение на ту же шкалу, получим изображение, длина которого будет , причём . Если теперь выбрать такой отрезок шкалы, чтобы на нём разместилось делений предмета и делений изображения, где и –целые числа и , то можно написать . Следовательно

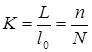. (1)

Если предмет расположен не так, как показано на рисунке, а пересекает ось прибора, то выражение для увеличения не изменится.

Измерения. Установив трубу на ясное видение удалённой на несколько метров линейки с делениями, смотрят на изображение этой линейки в трубу одним глазом, а другим – непосредственно на линейку. Устанавливают глаза так, чтобы изображение в трубе налагалось на видимую невооружённым глазом линейку и определяют количество целых делений шкалы линейки, совпадающих с целыми делениями её изображения. Увеличение вычисляют по формуле (1).

Этим же методом определить увеличение вспомогательной трубы (нивелира).

Второй метод . Известно, что между угловым увеличением оптической (зрительной) трубы и фокусным расстоянием составляющих её линз существует следующее соотношение:

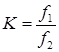где - главное фокусное расстояние объектива;

- окуляра.

Кроме того, в случае установленной на бесконечность трубы, длину её , то есть расстояние между объективом и окуляром, можно считать равным .

Если вывинтив объектив предварительно установленной на бесконечность трубы, поместить на его место предмет определённой величины (диафрагму с вырезом ), то по другую сторону окуляра на некотором расстоянии от него получится действительное изображение предмета величины , даваемое окуляром.

На основании формулы увеличения линзы имеем:

и .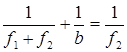

Исключив из этих двух уравнений, получим:

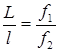то есть

. (2)

Измерения. Устанавливают трубу на бесконечность, то есть так, чтобы какой-нибудь удаленный предмет был ясно виден. Снимают объектив трубы и ставят на его место диафрагму с вырезом. Диафрагма имеет форму трёх скрещивающихся ромбов. Направляют трубу на освещенный белый экран. Помещают окуляр со шкалой (предварительно окулярную шкалу навести на резкость) перед окуляром трубы (окуляр трубы не вращать!), приближая или отдаляя окуляр со шкалой к окуляру трубы, добиваются на шкале окуляра получения отчётливого изображения скрещивающихся ромбов. Определяют поочередно число делений, занимаемых на шкале окуляра диагоналями ромбов. Штангенциркулем измеряют в той же очередности длину диагоналей ромбов непосредственно на диафрагме.

Если длина диагоналей ромбов равна , а длина их изображения на шкале окуляра , то увеличение трубы будет:

Измерения провести не менее трёх раз и результаты занести в таблицу 1 (первый метод) и в таблицу 2 (второй метод).

Таблица 1

№

изм

Число делений линейки

Соответствующее им число делений изображения

Увеличение трубы

К_ср

Таблица 2

№

изм

Число делений изображения диагоналей ромбов

Цена дел. ок. шкалы

мм

Длина изображений диагоналей ромбов

Длина диагоналей ромбов

К_ср

n₁

n₂

n₃

l₁

l₂

l₃

L₁

L₂

L₃

0,1

Упражнение 2

Определение поля зрения оптической трубы

Для определения поля зрения трубы её фокусируют на стенную линейку с делениями и замечают. Сколько делений этой линейки видимы в трубу. Затем измеряют рулеткой расстояние от объектива трубы до линейки. Если число делений линейки, видимых в трубу, равно , а расстояние от трубы до линейки равно , то поле зрения оптической трубы, выраженное в градусах, определяется формулой:

Измерения повести не менее 3-х раз и результаты занести в таблицу 3.

Таблица 3

№

Число делений линейки, видимых в трубу

Расстояние от трубы до линейки (см)

а=57,3

А_ср

Упражнение 3

Определение разрешающей способности оптических систем

Идеальная оптическая система, то есть такая система, которая не обладает аберрациями, согласно правилам геометрической оптики отображает каждую точку предмета (источника света) в виде точки. Идеальной оптической системой можно считать систему, в которой отображение производится параксиальными лучами. Отсюда следует, что, чем меньше отверстие системы, тем лучше должно быть изображение с точки зрения законов геометрической оптики.

Однако, как следует из теории дифракции на круглом отверстии, даже при идеальной оптической системе, то есть такой, в которой отсутствуют какие-либо аберрации, точечный источник отображается в виде кружка, угловая величина радиуса которого равна по первому дифракционному максимуму:

где –диаметр отверстия системы, а в случае линзы или зеркала (объекти ва) –диаметр входной линзы телескопа (микроскопа).

Если два точечных источника света находятся на угловом расстоянии, y то это принимается в качестве условия предельного разрешения двух близких светящихся точек (или двух близких точечных предметов).

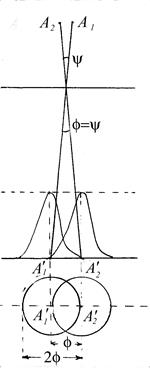
Рис. 2 .

На рис. 2 показано дифракционное изображение двух точечных источников А₁ и А₂ , удаленных друг от друга на расстояние , даваемое идеальной линзой (зеркалом или вообще оптической системой), имеющей диаметр оправы или диафрагмы (входного зрачка) . При таком расположении изображений наблюдаемых точечных источников А₁ и А₂ , дифракционное изображение каждого из них будет иметь диаметр (рис. 2). Поэтому при выбранном условии предельного разрешения максимум интенсивности в дифракционном изображении одной точки () располагается над минимумом интенсивности другой точки () и наоборот. Посредине результирующая интенсивность будет равна приблизительно 80% от интенсивности в максимуме (рис. 2). При этом наблюдатель ещё может различать два изображения. Если дальше сближать точки А₁ и А₂ , то имевшийся между и минимум результирующей интенсивности исчезает и оба изображения сольются в одно, то есть не будут восприниматься раздельно.

Таким образом, угловое расстояние между двумя светящимися объектами (точечными):

или ,

является пределом разрешения данной линзы (зеркала, телескопа, сложной оптической системы). Величина обратная принимается за разрешающую силу оптической системы:

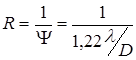Учитывая, что максимум спектральной чувствительности глаза приходится на =5,610^-4 мм, предыдущую формулу можно записать так

где ;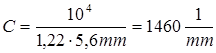

-диаметр оправы, диафрагмы, входного зрачка, линзы, выраженный

в мм.

В этом случае величина разрешающей силы указывает какое количество равноудаленных точек предмета, изображаемых линзой раздельно, приходится на единицу углового расстояния.

Реальная разрешающая сила линзы (оптической системы), как правило, ниже разрешающей силы, вычисленной по последней формуле, так как всякая линза обладает, в той или иной степени, аберрациями.

Разрешающую способность оптических приборов определяют при помощи тест-объектов абсолютного контраста в виде так называемых мир. Штриховая мира представляет собой набор групп семейств штрихов. В пределах одной группы штрихи четырёх семейств ориентированы друг по отношению к другу под углом 45^° и являются параллельными и одинаковыми по ширине. Ширина штрихов от группы к группе убывает в геометрической прогрессии. Каждая группа миры имеет свой номер. По прилагаемой таблице, зная номер группы, можно определить расстояние между двумя соседними одноименными штрихами в группе.

Для определения разрешающей силы линзы (оптической системы) мира располагается перед линзой на расстоянии, много большем фокусного расстояния линзы (телескопа, глаза, оптической системы).

Полученное уменьшенное изображение миры рассматривают с помощью окуляра, который, как известно, ни в коей мере на разрешающую силу объектива не влияет. При рассматривании изображения мир отыскивают такую группу семейств штрихов, в пределах которой штрихи всех четырёх направлений видны ещё раздельными, то есть не сливающимися в один общий серый фон. Определив номер этой группы, по таблице определяют расстояние между соседними одноименными штрихами. В этом случае реальная разрешающая сила линзы определится:

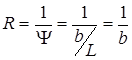, то есть

где – расстояние от миры до линзы в мм;

– расстояние между одноименными штрихами, выраженное в мм.

Определенная таким образом реальная разрешающая сила объектива всё же может оказаться заниженной по сравнению с истинным её значением. Это объясняется тем, что в качестве прибора, определяющего качество изображения миры, использовался глаз, сам имеющий ограниченный предел разрешения (для нормального глаза ).

Определим условия, при которых разрешающая сила глаза не будет влиять на результат определения разрешающей силы объектива. Положим, что изображение в объективе трубы разрешаемых им штрихов рассматривается через окуляр под углом не меньшим . В этом случае и изображение штрихов на сетчатке глаза также будет ещё не сливающимся.

Из чертежа хода лучей (рис. 3) можно определить

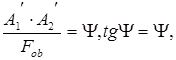аналогично .

Отсюда

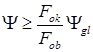или ;

где 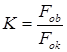- увеличение трубы.

Таким образом, приступая к определению разрешающей силы объектива необходимо убедиться, что предел разрешения объектива трубы по крайней мере не меньше .

В том случае, если , то определенная из опыта величина может не отражать истинное значение разрешающей силы объектива трубы, но является в этом случае разрешающей силой системы зрительная труба - глаз.

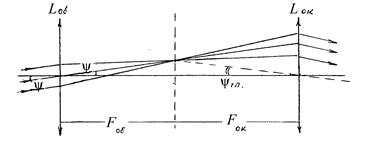
Рис. 3 .

Для уменьшения величины за испытываемой трубой устанавливается другая зрительная труба, такая, чтобы их общий коэффициент увеличения () позволил бы получить выполнение неравенств:

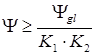где - увеличение трубы,- увеличение нивелира.

Вторая зрительная труба на разрешающую силу первой не оказывает влияния.

А. Определение предела разрешения глаза. Став перед мирой так, чтобы расстояние между глазом и мирой было, например, 1 метр, отыскивают такую группу семейств штрихов, в пределах которой штрихи всех четырёх направлений разрешаются (наблюдение ведется для того глаза, которым смотрят в трубу, второй глаз - закрыт). По номеру группы определите с помощью таблицы расстояние между одноименными штрихами и вычислите предел разрешения глаза:

Измерьте диаметр объектива модели зрительной трубы и рассчитайте ожидаемый предел разрешения :

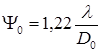Сравните величину и , где - увеличение трубы.

Таблица р асстояний между штрихами миры для глаза

№

Квадрата

b, мм

0,726

0,676

0,64

0,597

0,575

0,543

0,499

0,481

0,446

№ Квадрата	10	11	12	13	14	15	16
b, мм	0,428	0,41	0,377	0,356	0,332	0,316	0,302

Б. Определение предела разрешения систем зрительная труба – глаз. Для выполнения этого упражнения берется другая, с более густым расположением штрихов, мира, установленная на расстоянии порядка 7 метров. Наблюдая миру через трубу, убедитесь, что система труба – глаз не разрешает ни одной группы семейств штрихов данной миры. Однако это ещё ничего не говорит о качестве объектива.

В этом случае возможность наблюдения штрихов ограничивает алое увеличение трубы. Взяв отношение 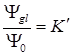, определим требуемое увеличение трубы. Легко убедится, что требуемое увеличение трубы больше фактического увеличения трубы, определенного в упражнении 1. Это говорит о том, что для проверки качества объектива необходимо вооружить глаз дополнительной трубой такой, чтобы произведение увеличения двух труб было бы больше .

Результаты измерений упражнений А и Б сведите в таблицу 4.

Таблица 4

фактич.

В. Определение разрешающей способности зрительной трубы. Поворачивая модель зрительной трубы и нивелир округ вертикальной оси, установите их вдоль одной общей оптической оси. Сняв модель зрительной трубы с её опорного штока, поверните установку на столе так, чтобы в поле зрения нивелира была видна мира, притом, как можно точнее в его центральной части. Затем, не меняя положения нивелира и всей установки, поместите модель зрительной трубы на её опорный шток, и, меняя её положение, добейтесь того, чтобы в центральной части поля зрения была расположена нижняя правая четверть миры. Проведя корректировку чёткости, определите разрешающую силу модели зрительной трубы с помощью миры методом, описанным для определения разрешающей силы глаза.

Таблица расстояний между штрихами миры для трубы

№ квадрата	1	2	3	4	5	6	7	8
b мм	0.195	0,183	0,172	0,161	0,151	0,145	0,134	0,129

№ квадрата	9	10	11	12	13	14	15	16
b мм	0,119	0,115	0,105	0,101	0,096	0,09	0,086	0,081

Результаты измерений свести в таблицу 5.

Таблица 5

D₀ =50mm

ВОПРОСЫПО ТЕМЕ.

1. Нарисуйте ход лучей в зрительной трубе.

2. Почему коэффициент увеличения зрительной трубы определяется отношением тангенсов углов, а не отношением размера изображения к размеру предмета?

3. Как изменится поле зрения, если в оптическую систему ввести рассеивающую линзу?

4. Напишите формулу для предельного угла разрешения линзы.

5. Что такое входной зрачок оптической системы?

6. В каких случаях разрешающая способность зрительной трубы определяется диаметром объектива, а в каких случаях – диаметром окуляра?

7. Определить предельный угол разрешения для глаза с диаметром зрачка D = 4 мм.

8. Почему днем невооруженным глазом звезды не видны, а в зрительную трубу с большим коэффициентом увеличения можно их увидеть?

9. Чему равен радиус первого максимума, при дифракции на линзе диаметром D и фокусным расстоянием f, при длине волны ?

ЛИТЕРАТУРА.

1. Г. С. Ландсберг, Оптика, 1976, §§87-94, стр. 318-340.

2. Д. В. Сивухин, Общий курс физики. Оптика, 1980, §§21-24, стр. 132-162.

3. Ф. А. Королев, Курс физики. Оптика, атомная и ядерная физика, 1974, §§35-39, стр. 208-229.

4. А. Н. Матвеев, Оптика, 1985, §§23-25, стр. 127-144.

5. И. В. Савельев, Курс физики, т. 3, 1967, §§14-15, стр. 51-57.

Скачать архив с текстом документа