Извлечение висмута из сульфидных многокомпонентных материалов гидрометаллургическим способом
СОДЕРЖАНИЕ: Исследован процесс выщелачивания висмута из сульфидного концентрата соляной кислотой. На основе полученной математической модели предложены оптимальные параметры процесса (концентрация кислоты, температура, время).Асп. Свистунов И.Ю., проф. Алкацев М.И. Кафедра металлургии цветных металлов. Северо-Кавказский государственный технологический университет
Исследован процесс выщелачивания висмута из сульфидного концентрата соляной кислотой. На основе полученной математической модели предложены оптимальные параметры процесса (концентрация кислоты, температура, время).
Целью исследования было извлечение висмута из сульфидного многокомпонентного концентрата, являющегося побочным продуктом одной из флотационных фабрик, выщелачиванием растворами соляной кислоты. Содержание висмута в концентрате составляло 0,52 %.
Выщелачивание проводили в термостатированном бутылочном агитаторе, позволяющем вести процесс в гидродинамическом режиме с высокой степенью воспроизводимости. Температуру поддерживали с точностью 0,5°С. Висмут определяли в растворах колориметричесим способом по ГОСТ 14047,4-78 на колориметре фотоэлектрическом концентрационном КФК-2МП.
Экспериментальное исследование проводили с использованием методов планирования экстремальных экспериментов (план Бокса В3). План Бокса, хотя и не является полностью ортогональным, тем не менее обладает высокой степенью D–оптимальности (минимальный определитель ковариационной матрицы) и меньшим числом необходимых опытов по сравнению с другими планами [1].
Матрица планирования эксперимента и результаты опытов по извлечению висмута в раствор приведены в таблице, в которой безразмерные переменные (Xi) связаны с размерными величинами следующим образом:
![]() ;
; ![]() ;
; ![]() , (1)
, (1)
где K – концентрация соляной кислоты, г/л; t - температура, оС; t - время, ч.
Обработку экспериментальных данных проводили методом наменьших квадратов, а в качестве математической модели использовали полином второй степени.
В результате математической обработки экспериментальных данных и отсева статистически незначимых (при уровне значимости 0,05) данных получено следующее полное уравнение регрессии (1) с безразмерным масштабом независимых переменных:
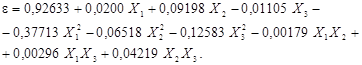 (2)
(2)
Матрица планирования и результаты эксперимента
| № | X1 | X2 | X3 | HCl, г/л | t, oC | t, ч | eэксп, доли | eрасч, доли |
| 1 | -1 | -1 | -1 | 80 | 40 | 1 | 0,3185 | 0,3006 |
| 2 | +1 | -1 | -1 | 120 | 40 | 1 | 0,3046 | 0,3383 |
| 3 | -1 | +1 | -1 | 80 | 80 | 1 | 0,3500 | 0,4037 |
| 4 | +1 | +1 | -1 | 120 | 80 | 1 | 0,4454 | 0,4343 |
| 5 | -1 | -1 | +1 | 80 | 40 | 5 | 0,1771 | 0,1882 |
| 6 | +1 | -1 | +1 | 120 | 40 | 5 | 0,2915 | 0,2378 |
| 7 | -1 | +1 | +1 | 80 | 80 | 5 | 0,4938 | 0,4601 |
| 8 | +1 | +1 | +1 | 120 | 80 | 5 | 0,4846 | 0,5025 |
| 9 | -1 | 0 | 0 | 80 | 60 | 3 | 0,5423 | 0,5291 |
| 10 | +1 | 0 | 0 | 120 | 60 | 3 | 0,5561 | 0,5692 |
| 11 | 0 | -1 | 0 | 100 | 40 | 3 | 0,7423 | 0,7692 |
| 12 | 0 | +1 | 0 | 100 | 80 | 3 | 0,9800 | 0,9531 |
| 13 | 0 | 0 | -1 | 100 | 60 | 1 | 0,8700 | 0,8115 |
| 14 | 0 | 0 | +1 | 100 | 60 | 5 | 0,7310 | 0,7894 |
Были получены следующие статистики, позволяющие оценить адекватность уравнения (1): R2 = 0,9757; F = 12,67; F0,05; 13; 4 = 5,89; Sад = 0,066.
Здесь R2 – коэффициент детерминации; F- расчетное значение F-статистики; F0,05; 13; 4 – табличное значение критерия Фишера; ![]() - средняя ошибка аппроксимации.
- средняя ошибка аппроксимации.
В связи с тем что F F0,05; 13; 4 , уравнение (2) признано адекватным экспериментальным данным с уровнем значимости 0,05.
В уравнении (2) коэффициенты регрессии b12 и b13 оказались статистически незначимыми при уровне значимости 0,05, в связи с чем были исключены, в результате было получено уравнение (3), являющееся также адекватным экспериментальным данным (F = 19,02).
После подстановки безразмерных переменных (1) в уравнение (3) получено сокращенное уравнение регрессии (4) с размерным масштабом независимых переменных:
![]() (3)
(3)
![]() (4)
(4)
R2 = 0,9757; F = 19,02; F0,05; 13; 6 = 4,02; Sад = 0,054.
В связи с тем что F F0,05; 13; 4 , уравнения (2) и (3) признаны адекватными экспериментальным данным с уровнем значимости 0,05.
На рисунке на основании уравнения (2) показаны графики частной зависимости извлечения висмута в раствор от концентрации кислоты в растворе, температуры и длительности процесса выщелачивания.
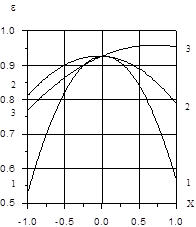
Частные зависимости извлечения висмута (e) от:
1 - концентрации соляной кислоты в растворе (Х1); 2 - температуры раствора (Х2); 3 – длительности выщелачивания (X3). Xi приведены в безразмерном масштабе в соответствии с (1).
При этом независимые переменные взяты в безразмерном масштабе и при варьировании одного из них, остальные взяты на основном (нулевом) уровне.
Методом нелинейного программирования в условиях ограничений на независимые переменные (+1 Xi -1), получены следующие значения переменных, позволяющие получить максимальное извлечение висмута:
emax = 0,9597 (95,97 %); HCl = 100,5 г/л; T = 74,6 оС; t = 3,1 ч.
Полученные экспериментальные данные находятся в согласии с литературными данными [2].
Заключение. Методом планирования эксперимента получены уравнения регрессии, связывающие извлечение висмута из концентрата выщелачиванием соляной кислотой. Найдены оптимальные условия эксперимента, позволяющие получить максимальное извлечение висмута.
Список литературы
Новик Ф.С., Арсов Я.Б. Оптимизация процессов технологии металлов методами планирования экспериментов. М.: Машиностроение. София: Техника, 1980. 304 с.
Металлургия висмута / Полывянный И.Р., Абланова А.Д., Батырбекова С.А., Сысоев Л.Н. Алма-Ата: Наука, 1973. 186 с.