Кинематика материальной точки

СОДЕРЖАНИЕ: РЕФЕРАТ На тему: Кинематика материальной точки Москва, 2010 Введение Кинематика это раздел физики, посвящённый математическому описанию движения без анализа причин, приводящих к его возникновению или изменению. Причиной изменения или возникновения движения является сила, а сила по II-у закону Ньютона связана с массой.

РЕФЕРАТ

На тему:

Москва, 2010

Введение

Кинематика - это раздел физики, посвящённый математическому описанию движения без анализа причин, приводящих к его возникновению или изменению. Причиной изменения или возникновения движения является сила, а сила по II-у закону Ньютона связана с массой. Поэтому для того, чтобы исключить из рассмотрения силу достаточно не рассматривать массу. При этом кроме силы из рассмотрения выпадают многие механические понятия: импульс, энергия, момент импульса. А что остаётся, то и рассматривается в кинематике. Таким образом, кинематику можно было бы назвать механикой без массы.

Самый простой объект, способный двигаться - это материальная точка: тело, размеры которого пренебрежимо малы в условиях данной физической задачи. Движением материальной точки называется смена её положения с течением времени. Поэтому первое кинематическое понятие, с которым мы сталкиваемся - это положение.

1. Вектор положения

Положение чего угодно невозможно задать само по себе. Всё находится относительно чего-то. Значит, мы должны сначала установить начало отсчёта (точку О), а это невозможно сделать по-другому, кроме как поставив туда какое-либо материальное тело (тело отсчёта). И от этого «главного» тела уже можно проводить геометрические векторы, соединяющие начало отсчёта с тем или иным положением материальной точки.

Геометрическим вектором называется направленный отрезок, соединяющий положения двух материальных точек.

Геометрический вектор, соединяющий тело отсчёта с материальной точкой, называется вектором положения материальной точки.

При задании положения материальной точки относительно тела отсчёта последнее по определению считается неподвижным. Поэтому все возможные векторы положений начинаются из одной точки и называются радиус-векторами .

Совокупность всех возможных радиус-векторов образует пространство.

Смена начала отсчёта приводит к изменению всех радиус-векторов. Каким образом? Ответ зависит от системы постулатов, которыми мы собираемся пользоваться. Классическая механика, которую мы в основном и изучаем, использует постулаты Галилея-Ньютона.

Если положение материальной точки М относительно тела отсчёта в точке О обозначить , относительно другого тела отсчёта в точке О обозначить , а геометрический вектор, соединяющий точки О и О , обозначить , то наблюдатель в точке О будет видеть три геометрических вектора: , и .

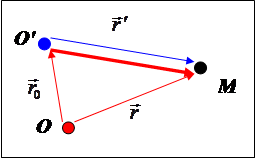
Пусть другому наблюдателю в точке О нет дела ни до чего, кроме материальной точки М . В дальнейшем системе отсчёта с нелюбопытным наблюдателем будет отводиться «второстепенная» роль. В противовес этому система с наблюдателем, который видит всё, будет считаться «основной». В общем, наблюдатель О видит только один вектор . Как соотносится геометрический вектор , видимый в пространстве О с геометрическим вектором , видимым в пространстве О ? Ответ на этот вопрос даёт первый постулат Галилея: геометрические векторы в разных системах отсчёта одинаковы. Т.е. . Тогда предыдущий рисунок можно переделать так:

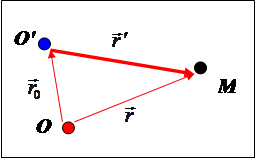
И правило сложения векторов по треугольнику позволяет записать соотношение между тремя векторами:

В соответствии с этим соотношением можно находить положения в «основной» системе отсчёта, зная их во «второстепенной». Такое преобразование радиус-векторов будем называть обратным преобразованием Галилея. Соответственно, прямое преобразование позволяет находить положения во «второстепенной» системе отсчёта, зная их в «основной»:

В дальнейшем какая-либо величина в «основном» пространстве будет называться «абсолютной », во «второстепенном» пространстве - «относительной» , а та, через которую они связаны, -переносной. Значит

· -«абсолютный» радиус-вектор;

· -«относительный» радиус-вектор;

· - переносный радиус-вектор.

Итак, в соответствие с первым постулатом Галилея смена начала отсчета приводит к изменению пространства, которое описывается преобразованием Галилея. Это означает, что пространство относительно.

2. Траектория движения

Используя понятие радиус-вектора, движение можно описать функциональной зависимостью , где t - время. Поскольку положение относительно, то и движение относительно. Относительны и все понятия, связанные с ним. Первым из таких понятий мы рассмотрим траекторию.

Траекторией называется совокупность положений, пройденных телом в процессе движения.

Тело не может в один и тот же момент времени находиться в разных положениях. Поэтому траектория представляет собой линию, и при этом линию непрерывную . В зависимости от формы траектории различают прямолинейное и криволинейное движение. Если криволинейная траектория лежит в одной плоскости, то движение называется плоским.

Если траектория представляет собой пространственную кривую, то в каждой точке траектории можно ввести понятие соприкасающейся плоскости .

Соприкасающейся плоскостью в какой-либо точке траектории М называется предельное положение плоскости, проходящей через три точки N, M, P этой траектории, когда точки N и P неограниченно приближаются (стремятся) к точке М.

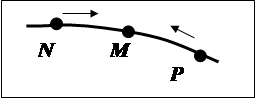
Через три точки, не лежащие на одной прямой можно прости окружность и при том единственную. Поэтому для любой точки криволинейной траектории можно ввести понятие соприкасающейся окружности.

Соприкасающейся окружностью в какой-либо точке траектории М называется предельная окружность, проходящая через три точки N, M, P этой траектории, когда точки N и P неограниченно приближаются (стремятся) к точке М.

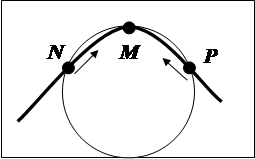
Центром и радиусом кривизны траектории в точке М называется центр и радиус кривизны окружности, соприкасающейся с траекторией в точке М. Очевидно, что в случае пространственной траектории соприкасающаяся окружность лежит в соприкасающейся плоскости. Прямолинейную траекторию можно считать траекторией с бесконечным радиусом кривизны.

Орт - это вектор, не обладающий физической размерностью (безразмерный), модуль которого равен единице. Любой вектор можно представить как произведение модуля на орт. Например, радиус-вектор:

Значит, орт любого вектора равен частному от деления вектора на его орт:

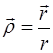Нормалью траектории в точке М называется орт, направленный из точки М в центр кривизны траектории в точке М.

Ортом касательной в точке М называется орт, касательный к соприкасающейся окружности в точке М и направленный по движению.

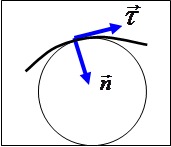
Ясно, что .

Перемещением называется вектор изменения положения или вектор разности между последующим положением и предыдущим:

В случае, если ни один отрезок траектории не проходился материальной точкой дважды, то путь или путевая координата S ( t ) - это длина траектории от точки начала движения к данному моменту времени.

Отметим две точки на траектории: M с радиусом-вектором и N с радиусом-вектором .

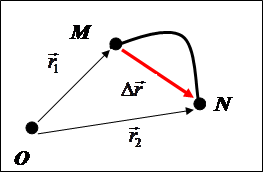
Тогда для перемещения и приращения пути D S всегда справедливо:

(равенство выполняется в случае прямолинейной траектории). При этом

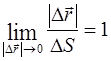
В случае криволинейной траектории элементарным перемещением и приращением пути dS называются такие, для которых с заданной наперёд точностью выполняется

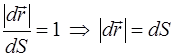
Очевидно, что

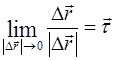т.е. .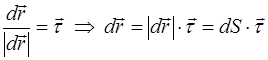

Итак, мы имеем связь между элементарными перемещением и приращением пути:

3. Скорость и ускорение движения

Средней скоростью движения называется отношение перемещения к промежутку времени, в течение которого произошло перемещение:

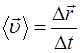Средней путевой скоростью называется отношение приращения пути к промежутку времени, в течение которого было пройдено это приращение:

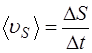Т.к. , то .

Мгновенной скоростью движения называется предел средней скорости при стремлении промежутка времени к 0:

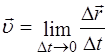Мгновенной путевой скоростью называется предел средней путевой скорости при стремлении промежутка времени к 0:

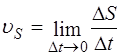Элементарным промежутком времени dt называется промежуток времени, для которого с заданной наперёд точностью и средняя, и средняя путевая скорость совпадают с соответствующими мгновенными скоростями.

Элементарным перемещением в произвольном случае назовём перемещение, произошедшее за элементарный промежуток времени dt . Элементарным приращением пути dS в произвольном случае назовём приращение, пройденное за элементарный промежуток времени dt.

Пользуясь языком высшей математики, мы можем сказать, что мгновенная скорость движения или просто скорость движения является первой производной радиус-вектора по времени, а путевая скорость является первой производной по времени путевой координаты.

; .

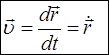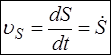Для того чтобы элементарное перемещение в произвольном случае совпадало с элементарным перемещением для криволинейной траектории нужно, чтобы точности вычисления соотношени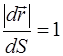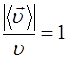й

; и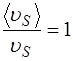

совпадали. Об этом всегда можно условиться. Поэтому мы всегда будем считать, что для элементарного промежутка времени , следовательно, , т.е.

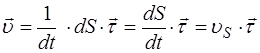Итак,

Т.е. модуль скорости движения совпадает с путевой скоростью. Конечное приращение пути по определению

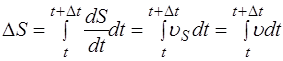
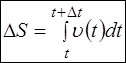По определению ускорением материальной точки называется первая производная по времени скорости движения, т.е. вторая производная по времени радиус-вектора:

Итак,

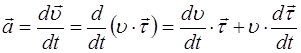
Первое слагаемое связано только со скоростью изменения величины скорости движения. Т.к. эта часть полного ускорения направлена по касательной, то она называется касательным ускорением .

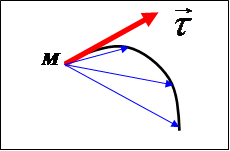
Второе слагаемое связано только с изменением направления скорости движения. Изобразим два положения материальной точки на траектории, разделённые элементарным приращением пути dS , и соответствующие орты касательной и . Соединим положения с центром кривизны траектории в точке dS .

Малый угол d a между радиусами совпадает с углом между ортами касательной как острые углы с взаимно перпендикулярными сторонами. Из второго рисунка видно, что направлен перпендикулярно , т.е. по орту нормали, а его величина

следовательно,

Угол d a связан с элементарным приращением пути dS = R d a , где R – радиус кривизны траектории. Отсюда 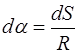. Подставим:

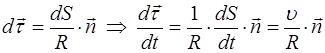Тогда вторая часть полного ускорения имеет вид:

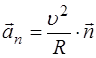Т.к. эта часть ускорения направлена по нормали, то она называется нормальным ускорением.

Сведём все формулы вместе:

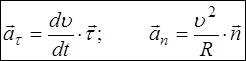
4. Относительность скорости движения

Мы уже пользовались понятием системы отсчёта, хотя делать этого не имели права. Из всех атрибутов системы отсчёта был введён только один: начало отсчёта. Другой атрибут – часы, находящиеся в начале отсчёта. Пусть двое часов находились в одной системе отсчёта, а потом «разошлись» по разным. Находясь в одном месте, они были синхронизованы. Как повлияет на их показания относительная скорость? Ответ на это опять зависит от выбора системы постулатов. В механике Ньютона-Галилея «работает» второй постулат Галилея : об абсолютности промежутков времени. Согласно этому постулату, если часы были синхронизованы, то их относительная скорость не влияет на их показания. Вспомним обратное преобразование Галилея для радиус-векторов: . Возьмём элементарные изменения (дифференциалы) от обеих частей этого равенства.

Поделим это равенство на элементарный промежуток времени по часам «основного» наблюдателя, в течение которого произошли элементарные перемещения, равенство останется верным:

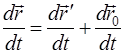В соответствие со вторым постулатом Галилея dt = dt , где dt – промежуток времени по часам «второстепенного» наблюдателя, в течение которого материальная точка переместилась относительно него на . Значит, можно записать:

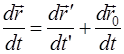Это обратное преобразование скорости по Галилею:

Прямое преобразование скорости:

5. Система координат

Для количественного описания движения в пространстве необходимо введение координат точки, т.е. совокупности чисел, однозначно определяющей положение материальной точки относительно начала отсчёта. Это возможно только в случае введения третьего атрибута системы отсчёта: системы координат. Теперь можно дать определение системы отсчёта: системой отсчёта называется система координат, в начале которой находится тело отсчёта, снабжённое часами.

В одномерном пространстве для задания «адреса» материальной точки достаточно одного числа, в двумерном пространстве – двух чисел, в трёхмерном – трёх чисел. Способов введения адресации – не один. Например, на плоскости можно задать полярную систему координат (угол, длина радиус-вектора), в пространстве сферическую (длина радиус-вектора, азимутальный угол и угол горизонта). Мы остановимся на подробном рассмотрении системы координат, связанной с разложением радиус-вектора.

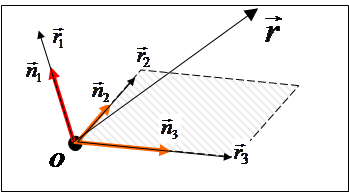
Известно, что любой вектор может быть представлен как сумма трёх векторов, направленных по трём наперёд заданным направлениям, не лежащим в одной плоскости .

Здесь – совокупность ортов, задающих направления. Она называется базисом системы отсчёта. – совокупность координат радиус-вектора в этом базисе. Т.к. вектор по трём избранным направлениям раскладывается однозначно, то однозначно и определение координат точки пространства.

Рассмотрим операцию скалярного умножения двух векторов и (например, радиус-векторов точек пространства А и В ):

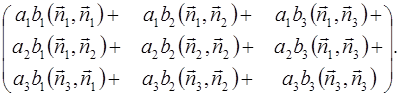
Всего девять слагаемых. Т.к. , то сумма диагональных элементов совсем проста: . Все остальные (перекрёстные члены) кроме произведения координат содержат множители типа

Выражение скалярного произведения можно существенно упростить, если выбрать углы 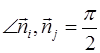. В этом случае говорят, что базис системы координат ортогональный. Только в ортогональном базисе

т.к. 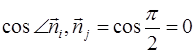и все перекрёстные члены равны 0. Именно в силу простоты записи скалярного произведения ортогональный базис является предпочтительным.

Впервые ортогональную систему координат (СК) ввёл Р. Декарт, и она называется декартовой. Только в декартовой СК

· координаты вектора являются его проекциями на соответствующую ось:

;

докажем это для первой координаты:

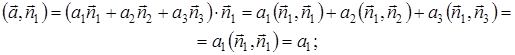
· координаты вектора связаны с его модулем соотношением Пифагора:

т.к. в соответствие с выражением скалярного произведения в декартовой системе.

Существуют традиционные обозначения декартовой СК.

Ось	Обозначение координаты	Обозначение орта
1	r ₁ = х
2	r ₂ = у
3	r ₃ =z

Таким образом, разложение радиус-вектора в декартовой СК будет иметь вид:

Векторную функцию движения можно заменить тремя скалярными зависимостями, которые называются законами движения: x(t), y(t), z(t).Законы движения содержат всю информацию о движении. Т.е. если известны законы движения, то можно ответить на любой вопрос, касающийся движения материальной точки.

· Скорость.

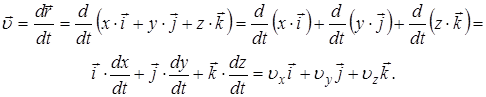
Таким образом, проекции вектора скорости равны производным соответствующих законов движения.

· Ускорение.

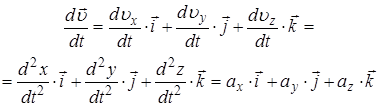Таким образом, проекции вектора ускорения равны вторым производным законов движения.

А как найти касательное и нормальное ускорения? Они являются результатом разложения вектора полного ускорения по направлениям касательной и нормали:

Касательный орт и орт нормали являются осями двумерного ортогонального базиса. Т.е. алгебраическое значение касательного ускорения представляет собой проекцию полного ускорения на орт :

Но касательный орт можно выразить через вектор скорости:

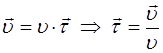Следовательно,

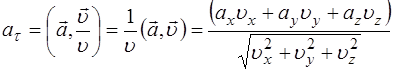Тогда легко получить:

А найдя нормальное ускорение, легко найти радиус кривизны:

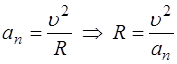
Заключение

Подведем некоторые итоги. Материальная точка представляет собой ключевую физическую модель. На примере этой модели рассматриваются очень многие физические явления. Описав движение материальной точки, можно затем перейти и к описанию движения твердого тела, но не наоборот.

Основными понятиями кинематики материальной точки являются понятия положения точки, ее скорости и ускорения. Но все эти понятия не имеют смысла вне системы отсчета, включающей в себя систему координат и часы.

Важнейшую роль в кинематике материальной точки играют векторная алгебра и принцип относительности движения.

Сложное движение материальной точки всегда можно разложить на составляющие, причем не однозначно: по координатам, на касательное и нормальное движение, прямолинейное и вращательное.

Литература

1. Мякишев Г.Я. Физика – 10. Механика. – М.: Дрофа. 2002.

2. Мякишев Г.Я., Синяков А.З. Физика – 10. Молекулярная физика. Термодинамика. – М.: Дрофа. 2002.

3. Мякишев Г.Я., Синяков А.З., Слободков Б.А. Физика – 10–11. Электродинамика. – М.: Дрофа. 2002.

4. Мякишев Г.Я., Синяков А.З. Физик – 11. Колебания и волны. – М.: Дрофа. 2002.

5. Демков В.П., Третьякова О.Н. В помощь поступающим в ВУЗы. Физика. Механика. – М.: Издательство МАИ, 1996.

6. Калашников Н.П., Смондырев М.А. Основы физики. Т.1. М.: Дрофа, 2003

7. Калашников Н.П., Смондырев М.А. Основы физики. Упражнения и задачи. М.: Дрофа, 2004.

8. Касаткина И.Л. Репетитор по физике. Т.1. Ростов н/Д: Феникс, 2002.

9. Новодворская Е.М., Дмитриев Э.М. Сборник задач по физике с решениями для втузов. М.: ООО Издательство «Мир и Образование», 2003.

Скачать архив с текстом документа