Коливальний рух

СОДЕРЖАНИЕ: Гармонічний коливальний рух та його кінематичні характеристики. Приклад періодичних процесів. Описання гармонічних коливань. Одиниці вимірювання. Прискорення тіла. Періодом гармонічного коливального руху. Векторні діаграми. Додавання коливань.

12. Коливальний рух.

1.Гармонічний коливальний рух та його кінематичні характеристики.

2.Описання гармонічних коливань. Векторні діаграми.

3.Додавання коливань.

1.Періодичними процесами називають такі зміни стану системи , при яких вона багато разів через деякі проміжки часу повертаємося в один і той же стан.

Прикладами періодичних процесів є обертання та коливання. Найпростішими коливаннями є так звані гармонічні коливання.

Гармонічним коливальним рухом називають рух, який описується рівнянням

або (12.1)

де : – миттєве значення зміщення в момент часу t;

–максимальне відхилення тіла, що коливається, від положення рівноваги;

Цю величину називають амплітудою;

називають фазою коливань, а її значення при t=0, тобто

- початковою фазою коливань;

- це циклічна (або кутова) частота.

Частотою називають число коливань , що здійснює система за одиницю часу.

Зв’язок між частотою v і циклічною частотою виражається співвідношенням:

(12.2)

Час протягом якого система здійснює одне коливання , називається періодом Т;

Зв’язок між Т та v:

Одиниці вимірювання:

Фаза – безрозмірна фізична величина.

Систему, що здійснює коливальний рух, називають також осцилятором; якщо рух описується рівнянням (12.1), то систему називають лінійним або гармонічним осцилятором.

Швидкість та прискорення тіла, що здійснює гармонічне коливання, знайдемо, взявши похідні від по t:

(12.4)

(12.5)

Порівнюючи вирази (12.5) та (12.1), одержимо:

(12.6)

або (12.7)

Під час гармонічного коливного руху прискорення тіла пропорціональне зміщенню від положення рівноваги і направлена протилежно зміщенню.

(12.6) чи (12.6’) називають рівнянням руху тіла, що здійснює гармонічний коливальний рух. Це диференціальне рівняння другого порядку; (12.1) є його розв’язком.

Уточнимо тепер поняття періоду:

Періодом гармонічного коливального руху називають найменший час, через який всі величини, що характеризують цей рух, набувають початкових значень.

Періоду відповідає зміна фази на :

2. Описання гармонічних коливань. Векторні діаграми.

Крім аналітичного способу описання гармонічних коливань – з допомогою рівняння , існує декілька способів графічного описання гармонічного коливного руху.

а) Плоскі діаграми – це графіки залежності від t (мал 12.1)

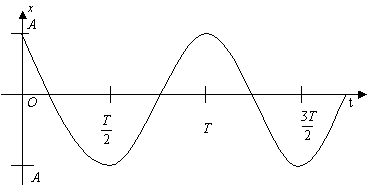
Мал.12.1.

.б) Якщо не цікавляться фазовими співвідношеннями, то зручним є спектральний метод описання гармонічного коливного руху – спектрограма (мал.12.2).

А (або )

v

Мал.12.2

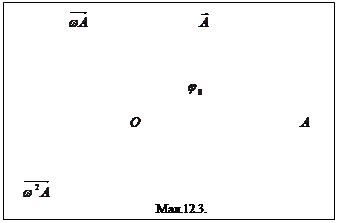
в) Метод векторних діаграм.

На площині вибирають довільний початок О і довільну вісь ОА. Гармонічна величина, що вивчається, наприклад, зміщення, уявляється вектором, який має довжину, пропорційну амплітуді, а кут між ним і віссю ОА дорівнює початковій фазі. В цьому випадку проекція вектора на вісь визначає миттєве зміщення в момент часу, рівне нулю. Якщо тепер уявити, що вектор рівномірно обертається навколо початку О з частотою руху, який вивчається,то в будь-який момент часу його проекція на вісь дає миттєве значення зміщення. (Умовимося вважати додатнім обертанням вектора проти годинникової стрілки).

г) Метод фазових діаграм.

На площині, яку називають фазовою площиною, вибирають прямокутну систему координат. По вісі абсцис відкладають зміщення x, а по вісі ординат – швидкість (у випадку гармонічного коливного руху – “приведену швидкість ” ).

Стан руху в кожний момент часу зображається точкою з координатами , що відповідають даному моменту часу. З плином часу ця точка описує на площині криву , яку називають “фазою траєкторії ”. Для гармонічного коливання руху з (12.1) і (12.4) одержимо:

Це рівняння кола радіусом А з центром початку координат (мал. 12.4). На мал.12.5 – 12.7 наведено для прикладу фазові діаграмми ще для деяких рухів.

Мал 12.4. Мал.12.5.Рывномырний рух.

Мал.12.6.

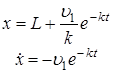
Мал.12.7. Рідке тертя.

3.Додавання коливань.

а) Додавання коливань одного напрямку.

1). Нехай коливання мають однакові частоти

Для спрощення початкова фаза першого дорівнює нулю. Скористаємося методом векторних діаграм:

Далі буде показано, що повна енергія тіла, що коливається, пропорційна квадрату амплітуди; тому (12.7) можна представити так:

(12.9)

Повна енергія залежить від різниці фаз і може бути як більше, так і менше суми енергії коливань, що додаються. Даний випадок називають Інтерференцією, а коливання, що задовольняють умові незмінності початкових фаз з часом – когерентними.

2).Якщо частоти коливань різні , то одержується складне не гармонічне коливання. При , але , виникають коливання з періодичною зміною амплітуди, які називаються биттям.

Нехай

X А t Мал.12.9. Мал.12.10.

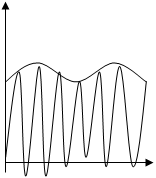б)Додавання взаємно перпендикулярних коливань. Фігури лісажу.

В загальному виді коливання задаються рівняннями:

Розглянемо окремі випадки.

1)

або

Це – відрізок прямої.

2)

При

КОЛО.

ЕЛІПС.

При , але (чи ) де k ціле число (k=2,3,4…), одержуються більш складні фігури, які дістали назву фігур Лісажжу. Спостерігати ці фігури можна на екрані осцилографа, подаючи на його входи “” та “” коливання від двох генераторів. Форма фігур залежить від співвідношення частот і різниці фаз коливань, що додаються (мал. 12.11).

Скачать архив с текстом документа