Контрольная работа по Статистике 17
СОДЕРЖАНИЕ: Академия ФсиН России Экономический факультет Кафедра математики и информационных технологий управления КОНТРОЛЬНая работа по дисциплине «Статистика»Академия ФсиН России
Экономический факультет
Кафедра математики и информационных технологий управления
КОНТРОЛЬНая работа
по дисциплине «Статистика»
Работу выполнила:
Студентка 4 курса
Пчёлкина (Мозговая) Л. В.
Группа: 4531
Специальность: бухгалтерский учёт, анализ, аудит
Шифр: 080109.65
з/к № 1544
Руководитель:
Дауров В. Г.
Рязань 2010 г.
Задача № 5
Имеются следующие отчетные данные 24 заводов одной:
| № завода | Среднегодовая стоимость основных производственных фондов, млн. руб. | Товарная продукция, млн. руб. |
| 1 | 6,4 | 7,5 |
| 2 | 3,9 | 6,0 |
| 3 | 0,4 | 0,4 |
| 4 | 2,0 | 2,6 |
| 5 | 2,2 | 2,4 |
| 6 | 2,8 | 2,8 |
| 7 | 2,1 | 2,4 |
| 8 | 4,5 | 5,4 |
| 9 | 6,4 | 8,3 |
| 10 | 3,5 | 3,8 |
| 11 | 3,6 | 5,6 |
| 12 | 1,9 | 1,6 |
| 13 | 2,3 | 2,5 |
| 14 | 0,7 | 0,6 |
| 15 | 3,8 | 4,3 |
| 16 | 1,8 | 1,8 |
| 17 | 2,2 | 3,6 |
| 18 | 3,4 | 4,2 |
| 19 | 2,3 | 3,4 |
| 20 | 2,9 | 3,4 |
| 21 | 5,8 | 6,5 |
| 22 | 3,7 | 5,2 |
| 23 | 5,4 | 7,8 |
| 24 | 3,5 | 4,5 |
С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском товарной продукции произведите группировку заводов по среднегодовой стоимости основных производственных фондов, образовав четыре группы заводов с равными интервалами. По каждой группе из совокупности заводов определите:
1) число заводов;
2) среднегодовую стоимость основных производственных фондов – всего и в среднем на один завод;
3) стоимость товарной продукции – всего и в среднем на один завод.
Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Решение.
Определим шаг интервала по формуле:
i =1,5 млн. руб.
Определяем границы групп:
I. 0,4 – 1,9
II. 1,9 – 3,4
III. 3,4 – 4,9
IV. 4,9 – 6,4
Составляем рабочую таблицу.
Таблица 1.
Рабочая таблица
| № п/п | Группы заводов по среднегодовой стоимости основных производственных фондов, млн. руб. | № завода | Среднегодовая стоимость основных производственных фондов, млн. руб. | Товарная продукция, млн. руб. |
| I | 0,4 – 1,9 | 3 | 0,4 | 0,4 |
| 12 | 1,9 | 1,6 | ||
| 14 | 0,7 | 0,6 | ||
| 16 | 1,8 | 1,8 | ||
| Итого: | 4 | |||
| II | 1,9 – 3,4 | 4 | 2,0 | 2,6 |
| 5 | 2,2 | 2,4 | ||
| 6 | 2,8 | 2,8 | ||
| 7 | 2,1 | 2,4 | ||
| 13 | 2,3 | 2,5 | ||
| 17 | 2,2 | 3,6 | ||
| 18 | 3,4 | 4,2 | ||
| 19 | 2,3 | 3,4 | ||
| 20 | 2,9 | 3,4 | ||
| Итого: | 9 | |||
| III | 3,4 – 4,9 | 2 | 3,9 | 6,0 |
| 8 | 4,5 | 5,4 | ||
| 10 | 3,5 | 3,8 | ||
| 11 | 3,6 | 5,6 | ||
| 15 | 3,8 | 4,3 | ||
| 22 | 3,7 | 5,2 | ||
| 24 | 3,5 | 4,5 | ||
| Итого: | 7 | |||
| IV | 4,9 – 6,4 | 1 | 6,4 | 7,5 |
| 9 | 6,4 | 8,3 | ||
| 21 | 5,8 | 6,5 | ||
| 23 | 5,4 | 7,8 | ||
| Итого: | 4 | |||
По рабочей таблице составим итоговую групповую таблицу.
Таблица 2
Групповая таблица
| № п/п | Группы заводов по среднегодовой стоимости основных производственных фондов, млн. руб. | Число заводов | Среднегодовая стоимость основных производственных фондов, млн. руб. | Товарная продукция, млн. руб | ||
| Всего | В среднем на один завод | Всего | В среднем на один завод | |||
| I | 0,4 – 1,9 | 4 | ||||
| II | 1,9 – 3,4 | 9 | ||||
| III | 3,4 – 4,9 | 7 | ||||
| IV | 4,9 – 6,4 | 4 | ||||
| В целом: | ||||||
Выводы: чем выше среднегодовая стоимость основных фондов, тем больше имеем товарной продукции.
Задача № 9
Имеются следующие данные о списочной численности шоферов автопарка за сентябрь:
| Числа месяца | Состояло по списку чел. |
Числа месяца | Состояло по списку чел. |
1-5 6-7 8-11 |
90 93 92 |
12-19 20 21-30 |
105 103 109 |
Определите среднесуточное число шоферов за сентябрь.
Решение.
Определим среднесуточное число шоферов за сентябрь по формуле средней арифметической взвешенной:
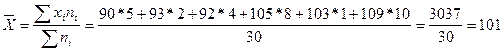чел.
Задача № 15
В результате 5%-го бесповторного выборочного обследования 200 работников предприятия общественного питания, отобранных в случайном порядке, получены следующие данные о годовой выработке продукции:
| Группы работников по выработке продукции, тыс. руб. | Число работников, чел. |
| До 600 | 20 |
| 600-800 | 30 |
| 800-1000 | 70 |
| 1000-1200 | 50 |
| свыше 1200 | 30 |
| ИТОГО | 200 |
На основе этих данных вычислите:
1) среднюю выработку продукции на одного работника;
2) средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение;
3) коэффициент вариации;
4) с вероятностью 0,954 предельную ошибку выборочной средней и возможные границы, в которых ожидается среднегодовая выработка продукции работниками предприятий общественного питания;
5) с вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса числа работников предприятий общественного питания, годовая выработка которых составляет от 800-1200 тыс. руб.
Решение.
Запишем исходные данные в виде таблицы 1.
Таблица 1.
| Группы работников по выработке продукции, тыс. руб. | В среднем в группе xi , тыс. руб. | Число работников, чел. |
| До 600 | 20 | |
| 600-800 | 30 | |
| 800-1000 | 70 | |
| 1000-1200 | 50 | |
| свыше 1200 | 30 | |
| ИТОГО | 200 |
1) средняя выработка на 1 работника равна
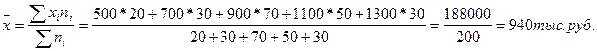
2) дисперсия равна
Среднее квадратическое отклонение равно
3) коэффициент вариации
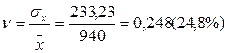
4) определим с вероятностью 0,954 предельную ошибку выборочной средней и возможные границы, в которых ожидается среднегодовая выработка продукции работниками предприятий общественного питания.
По условию задачи имеем 5% бесповторную выборку, т.к. обследовано 5% работников, то
При р=0,954, коэффициент доверия t=2. тогда предельная ошибка выработки равна
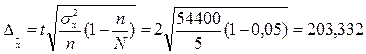
Определим возможные границы, в которых находится средняя выработка продукции работниками предприятий общественного питания.
Подставим имеющиеся данные:
940-203,332
940+203,332
736,6681143,332
5) определим с вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса числа работников предприятий общественного питания, годовая выработка которых составляет от 800-1200 тыс. руб.
Выборочная доля числа работников, годовая выработка которых от 800-1200 тыс. руб. составляет:
W=120/200=0,6 (60%)
Отсюда дисперсия доли равна:
=W(1-W)=0,6*0,4=0,24
Тогда предельная ошибка выборки равна:
при р=0,997, t=3
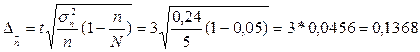
Определим возможные границы удельного веса числа работников предприятий общественного питания, годовая выработка которых составляет от 800-1200 тыс. руб.
Получим:
0,6-0,1368
0,6+0,1368
0,46320,7368
или
46,32%73,68%
Задача № 20
Остатки вкладов в сберегательных банках района характеризуются следующими данными, млн. руб.:
| На 1 января | - 203 | На 1 мая | - 214 | На 1 сентября | - 206 |
| На 1 февраля | - 205 | На 1 июня | - 215 | На 1 октября | - 210 |
| На 1 марта | - 210 | На 1 июля | - 216 | ||
| На 1 апреля | - 211 | На 1 августа | - 211 |
Вычислите средний остаток вкладов: за каждый квартал и за 9 месяцев в целом.
Объясните выбор метода расчета средней.
Решение.
Вычислим средний остаток вкладов за каждый квартал:
· январь-март:
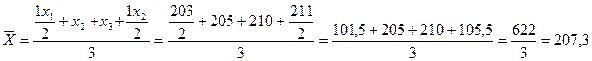млн. руб.
· апрель-июнь:
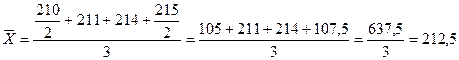млн. руб.
· июль-сентябрь:
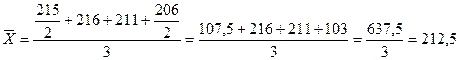млн. руб.
· 9 месяцев в целом:
млн. руб.
Задача № 26
Объемы производства и себестоимости одного и того же вида продукции по трем предприятиям составили:
| Предприятия | Произведено продукции, шт. | Себестоимость единицы, руб. | ||
| Базисный период | Отчетный период |
Базисный период | Отчетный период | |
1 2 3 |
678 750 580 |
702 818 720 |
1260 1100 989 |
1256 1110 980 |
Вычислите индексы себестоимости переменного и постоянного составов и индекс влияния структурных сдвигов на изменение средней себестоимости продукции. Проанализируйте результаты.
Решение.
Индекс переменного состава равен:
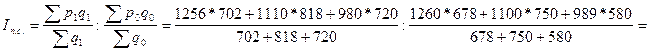
(99,28%)
Индекс постоянного состава равен:
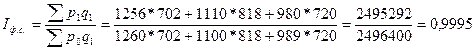(99,95%)
Индекс структуры равен:
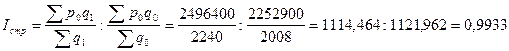(99,33%)
(99,33%)
Средняя себестоимость продукции уменьшилась на 0,72 % за счет уменьшения его себестоимости на каждом предприятии.
Средняя себестоимость продукции уменьшилась на 0,67 % за счет изменения структуры производства.
Вывод: Средняя себестоимость продукции уменьшилась в большей степени за счет уменьшения себестоимости продукции каждого из предприятий.
Задача № 32
В результате проведенного исследования по 10 предприятиям фирмы получены следующие данные:
№ пред- приятия |
Выработка продукции на одного рабочего, тыс. руб. | Объем произведенной продукции, тыс. руб. |
| 1 | 18 | 72 |
| 2 | 24 | 120 |
| 3 | 27 | 108 |
| 4 | 30 | 120 |
| 5 | 30 | 135 |
| 6 | 33 | 138 |
| 7 | 36 | 168 |
| 8 | 39 | 195 |
| 9 | 42 | 210 |
| 10 | 45 | 150 |
| ИТОГО | 324 | 1416 |
Найдите уравнение регрессии зависимости выработки рабочего от объема производительности труда.
Решение.
Линейная регрессия: yx =a+bx
коэффициенты a, b регрессионной модели находятся моментом наименьших квадратов, решая систему линейных уравнений:
an+bx=y,
ax+bx2 =xy,
где n – число предприятий, n=10
Для решения составим расчетную таблицу:
Таблица 1
| № | y | x | y2 | x2 | xy |
| 1 | 18 | 72 | 324 | 5184 | 1296 |
| 2 | 24 | 120 | 576 | 14400 | 2880 |
| 3 | 27 | 108 | 729 | 11664 | 2916 |
| 4 | 30 | 120 | 900 | 14400 | 3600 |
| 5 | 30 | 135 | 900 | 18225 | 4050 |
| 6 | 33 | 138 | 1089 | 19044 | 4554 |
| 7 | 36 | 168 | 1296 | 28224 | 6048 |
| 8 | 39 | 195 | 1521 | 38025 | 7605 |
| 9 | 42 | 210 | 1764 | 44100 | 8820 |
| 10 | 45 | 150 | 2025 | 22500 | 6750 |
| ИТОГО | 324 | 1416 | 11124 | 215766 | 48519 |
Подставим в систему уравнений найденные значения сумм:
10a+1416b=324,
1416a+215766b=48519
a+141,6b=32,4,
a+152,4b=34,3
10,8b=1,9 b=0,2
a+0,2*141,6=32,4
a=32,4-28,3 a=4,1
a=4,1; b=0,2
Уравнение линейной регрессии примет вид:
yx =4,1+0,2x
Раздел «СОЦИАЛЬНО-ЭКОНОМИЧЕСКАЯ СТАТИСТИКА»
Задача № 4
Численность населения города составила на начало года 69 200 человек, на конец года - 71 834. Коэффициент естественного прироста населения города составил за год 8,0 промилле.
Определите:
1) механический прирост и коэффициент механического прироста населения за год;
2) коэффициент жизнеспособности, если коэффициенты смертности и механического прироста равны.
Решение.
Введем следующие обозначения: N – число родившихся, M – число умерших, S – средняя численность населения. Тогда формулы расчета коэффициентов рождаемости (KN ), смертности (KM ) и естественного прироста (K ) следующие:
,
,
.
1) По условию задачи коэффициент естественного прироста K равен 8,0 ‰. Следовательно, естественный прирост составил:
чел.
Общий прирост населения за год составил:
SK - SH =71834-69200=2634 чел.
Таким образом, механический прирост населения за год составил:
( SK - SH )-( N - M ) = 2634-554=2080 чел.
Тогда коэффициент механического прироста населения за год равен:
‰
2) Найдем коэффициент жизнеспособности, если коэффициент смертности KM = коэффициенту механического прироста = 2080 чел.
Число родившихся за год составило:
чел.
Тогда коэффициент жизнеспособности равен:
Задача № 9
Из 35 станков на фирме фактически работало 30. В том числе в две смены - 12 шт., в три смены - 18 шт. Число дней работы - 26, режим работы трехсменным, продолжительность смены - 7 час., а в предвыходные дни - 6 час. Обработано за месяц 464 660 деталей. Простои в течение месяца были равны 560 станко-часам.
Определите:
1) календарный фонд установленного оборудования;
2) режимный фонд установленного оборудования;
3) количество фактически отработанных станко-часов;
4) производительность одного станка в час.
Решение.
1) календарный фонд установленного оборудования равен произведению числа дней на кол-во установленных станков
ТФ= 26*35 =910 станко-дней
2) режимный фонд установленного оборудования равен произведению длительности трехсменной работы на число дней работы и на кол-во установленных станков.
РФ = 21*26*35 = 19110
3) количество фактически отработанных станко-часов составило:
14*26*12+21*26*18-560 = 14196-560 = 13636 станко-часов
4) производительность одного станка в час составила:
детелей
Задача № 13
Имеются данные по ООО «Пустотино» за два смежных года:
| Виды зерновых | Посевная площадь, га | Урожайность, ц/га | ||
| базисный период | отчетный период | базисный период | Отчетный период | |
| Пшеница озимая | 200 | 170 | 25 | 23 |
| Ячмень | 70 | 110 | 20 | 25 |
| Кукуруза | 20 | 23 | 41 | 42 |
Определите:
1) индексы урожайности отдельных культур;
2) общие индексы урожайности переменного и фиксированного состава;
3) индекс влияния изменения структуры посевных площадей на динамику средней урожайности;
4) общие индексы посевной площади и валового сбора, их взаимосвязь с индексом урожайности;
5) на сколько изменилась средняя урожайность (в центнерах) по сравнению с базисным периодом за счет изменения урожайности отдельных культур и за счет изменения структуры посевных площадей;
6) прирост валового сбора (в центнерах) по сравнению с базисным периодом за счет изменения:
а) урожайности отдельных культур;
б) структуры посевных площадей;
в) размера посевной площади.
Решение.
1) индексы урожайностиip
вычисляются по формуле: 
.
Пшеницы: 
или 92,0%
Ячменя: 
или 125,0%
Кукурузы: 
или 102,4%
2) найдем общие индексы урожайности переменного и фиксированного состава
Индекс урожайности переменного состава:
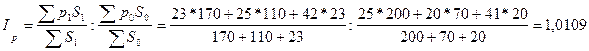
Индекс урожайности фиксированного состава:
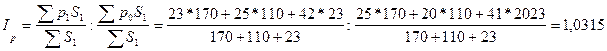
3) индекс влияния изменения структуры посевных площадей на динамику средней урожайности:
.
4) общий индекс посевной площади равен:
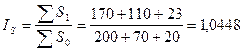или 104,48%
общий индекс валового сбора равен:
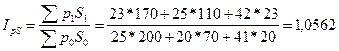или 105,62%
Общие индексы посевной площади и валового сбора связаны с индексом урожайности следующим равенством: 
.
В нашем случае 
верно.
5) определим, на сколько изменилась средняя урожайность (в центнерах) по сравнению с базисным периодом за счет изменения урожайности отдельных культур и за счет изменения структуры посевных площадей.
Средняя урожайность (в центнерах) в отчетном периоде по сравнению с базисным периодом изменилась на:
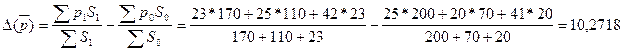ц/га.
За счет изменения урожайности отдельных культур это изменение составило:
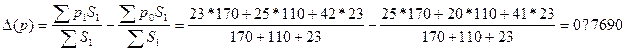ц/га.
За счет изменения структуры посевных площадей составило:
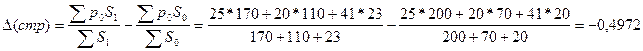ц/га.
6) определим прирост валового сбора (в центнерах) по сравнению с базисным периодом за счет изменения:
а) урожайности отдельных культур
Прирост валового сбора (в центнерах) в отчетном периоде по сравнению с базисным периодом за счет изменения урожайности отдельных культур составил:
б) структуры посевных площадей
Прирост валового сбора в отчетном периоде по сравнению с базисным периодом за счет изменения структуры посевных площадей составил:
ц/га
в) размера посевной площади
Прирост валового сбора в отчетном периоде по сравнению с базисным периодом за счет изменения размера посевной площади составил:
ц
Задача № 20
Товарооборот магазина за отчетный период был равен 1000 тыс. руб. Средняя численность работников магазина - 25 человек. Индекс цен - 1,09. Средний оборот на одного работника в базисном периоде - 200 тыс. руб.
Найдите индекс производительности труда в неизменных ценах.
Решение.
Производительность труда в отчетный период составила:
тыс. руб. на одного работника.
Поскольку индекс цен ip = 1,09, то производительность труда в неизменных ценах равна:
тыс. руб. на одного работника.
Тогда индекс цен производительности труда в неименных ценах в отчетном периоде по сравнению с базисным равен:
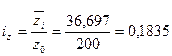или 18,35%
Задача № 27
Исчислите недостающие показатели производства и транспортировки одноименной продукции.
| Показатели | Базисный период | Отчетный период | Индексы |
| Произведено, тыс. т | 50 | 1,25 | |
| Перевезено, тыс. т | 40 | ||
| Грузооборот, млн. т-км | 1,1 | ||
| Средняя дальность перевозок, км | 1000 | ||
| Коэффициент перевозимости | 0,84 |
Решение.
Найдем объем произведенной продукции:
тыс.т.
Коэффициент перевозимости в отчетном периоде исчисляется по формуле:
или 64%
Найдем коэффициент перевозимости в базисном периоде:
или 76%
Определим объем перевезенной продукции в базисном периоде:
тыс.т.
Определим грузооборот продукции в базисном периоде:
тыс. т-км.
Определим грузооборот продукции в отчетном периоде:
тыс. т-км.
Определим индекс перевозимости продукции:
или 102%
Средняя дальность перевозок будет равна:
км
Индекс средней дальности перевозок:
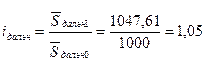или 105%
Таким образом, получим следующие результаты:
| Показатели | Базисный период | Отчетный период | Индексы |
| Произведено, тыс. т | 50 | 62,5 |
1,25 |
| Перевезено, тыс. т | 38,09 |
40 | 1,02 |
| Грузооборот, млн. т-км | 3809 |
41904,5 |
1,1 |
| Средняя дальность перевозок, км | 1000 | 1047,61 |
1,05 |
| Коэффициент перевозимости | 0,76 |
0,64 |
0,84 |
Задача № 33
Имеются следующие данные о расходах населения:
| Товары и услуги | Стоимость приобретения товаров и услуг, млн. руб. | Изменение цен в отчетном периоде по сравнению с базисным, % |
|
| Базисный период | Отчетный период | ||
| Непродовольственные товары | 72 | 78 | -9,5 |
| Продовольственные товары | 89 | 93 | +8,2 |
| Бытовые услуги | 10 | 15 | +10,1 |
Определите:
1) изменение объема потребления населением по каждому виду товаров и услуг и изменение общего объема потребления по всем видам потребления;
2) экономию (потери) населения за счет изменения цен.
Решение.
1) изменение объема потребления населением по каждому виду товаров и услуг находится по формуле:
По непродовольственным товарам:
или 119,71%,
т. е. увеличение составило 19,71%
По продовольственным товарам:
или 96,58%
т. е. увеличение составило 3,42%
По бытовым услугам:
или 136,24%
т. е. увеличение составило 36,24%
2) определим экономию (потери) населения за счет изменения цен:
млн. руб.
Таким образом, дополнительные потери населения за счет изменения цен в отчетном периоде по сравнению с базисным составили 0,2362 млн. руб.
Список литературы:
1. Статистика. Учебник / Под редакцией проф. И.И. Елисеевой. – М.: ООО «ВИТРЭМ», 2002 г.
2. Практикум по курсу социально-экономической статистики: Учеб. пособие / Под редакцией М.Г. Назарова. – М.: Финансы и статистика, 1983 г.
3. Статистика. Учебно-практич. пособие / Под ред. М.Г.Назарова. – М.: КНОРУС, 2006 г.