Конвейерная система
СОДЕРЖАНИЕ: Министерство Образования и Науки Российской Федерации Дагестанский Государственный Технический Университет Кафедра ИСвЭ Курсовая работа по дисциплине: ИМЭПМинистерство Образования и Науки Российской Федерации
Дагестанский Государственный Технический Университет
ФИС
Кафедра ИСвЭ
Курсовая работа
по дисциплине: ИМЭП
«Конвейерная система»
Выполнила: ст-ка 4 к. гр.И-215
Ахмедова А.А.
Проверила: Расулова М.М.
Махачкала 2005г.
Содержание.
1. Введение.
2. Постановка задачи.
3. Описание метода решения.
4. Разработка модели:
· Формализованная схема
· Временная диаграмма
· Блок-схема
5. Перевод модели на язык программирования.
1. Введение.
Имитационное моделирование основано на прямом описании моделируемого объекта. Существенной характеристикой таких моделей является структурное подобие объекта и модели. Это значит, каждому существенному с точки зрения решаемой задачи элементу объекта ставится в соответствие элемент модели. При построении имитационной модели описываются законы функционирования каждого элемента объекта и связи между ними. Работа с имитационной моделью заключается в проведении имитационного эксперимента. Процесс, протекающий в модели в ходе эксперимента, подобен процессу в реальном объекте. Поэтому исследование объекта на его имитационной модели сводится к изучению характеристик процесса, протекающего в ходе эксперимента
Для формального представления процессов функционирования систем при имитационном моделировании обычно используются два типа схем, схема с дискретными событиями и непрерывные схемы. При дискретной схеме процесс функционирования системы во времени отождествляется с последовательностью событий, возникающих в системе в соответствии с закономерностями ее функционирования. В формальное понятие «событие» вкладывается конкретное смысловое содержание, определяемое целями моделирования. При непрерывной схеме процесс задается с помощью системы уравнений для совокупности переменных состояния, динамическое поведение которых имитирует реальную систему.
Ценным качеством имитации является возможность управлять масштабом времени. Динамический процесс в имитационной модели протекает в так называемом системном времени. Системное время имитирует реальное время. При этом пересчет системного времени в модели можно выполнять двумя способами: Первый заключается в «движении» по времени с некоторым постоянным шагом t, второй - в «движении» по времени от события к событию. Считается, что в промежутках времени между событиями в модели изменений не происходит.
Кроме реального и системного времени существует ещё один тип времени - машинное, т.е. время, за которое реализуется имитационный эксперимент. При имитационном моделировании реальных систем, как правило, стремятся «сжать» реальное время, т.е. продолжительность процессов в модели, измеряется машинным временем, значительно меньше продолжительности тех же процессов в реальном объекте. Это дает возможность изучать функционирование реальной системы на достаточно длительных интервалах времени.
Очевидно, аналогичные задачи можно решать и с помощью аналитических методов, однако имитация позволяет работать с моделями большой размерности, учитывать ограничения и условия, которые трудно или невозможно включить в аналитическую модель, а также представлять результаты моделирования в наглядной легко интерпретируемой форме. Однако это не значит, что имитационное моделирование может заменить аналитическое. Проведение имитационного эксперимента часто оказывается трудоемкой и длительной процедурой. Поэтому на практике при решении задач анализа и управления в экономических системах аналитическое и имитационное моделирование объединяют в комплексную процедуру. Аналитическое моделирование в такой процедуре используют для быстрого, но приближенного оценивания основных характеристик систем, что позволяет выявить некоторые закономерности в поведении системы и сформулировать требования к системе управления. Имитационное моделирование занимает больше времени и позволяет определить указанные характеристики и другие с более высокой степенью точности.
Имитационное моделирование реализуются программно с использованием различных языков, как универсальных - БЕЙСИК, РАСКАЛЬ, СИ и т.д., так и специализированных, предназначенных для построения имитационных моделей - СИМСКРИПТ, GPSS, СТАМЛСЛАСС, SLAM, Pilgrim и др.
Цель курсовой работы по дисциплине «Имитационное моделирование экономических процессов» состоит в том, чтобы разработать имитирующую модель конвейерной системы.
2. Постановка задачи.
Два обслуживающих устройства установлено у ленты конвейера и, если они свободны, могут снимать изделия с конвейера. Изделия поступают на первый конвейер с постоянным интервалом, равным 10 единицам времени. Изделию, попавшему на конвейер, требуется 3 единицы времени, чтобы достичь первого обслуживающего устройства. Если первое устройство занято, изделие продолжает двигаться по ленте конвейера и через 3 единицы времени достигает второго обслуживающего устройства. Если оба устройства заняты, то изделие возвращается к устройствам через 9 единиц времени (если оно не будет снято другим устройством). Время обслуживания изделия распределено нормально с математическим ожиданием 5,0 и среднеквадратичным отклонением 1. Когда устройство у первой ленты завершает обработку изделия, оно помещает его на ленту второго конвейера, обслуживаемого другим устройством. Изделия поступают к третьему устройству через 5 единиц времени после попадания на второй конвейер. Если третье обслуживающее устройство занято, то изделие остается на ленте конвейера и через 12 единиц времени снова попадает к этому устройству. Время обслуживания третьего устройства распределено экспоненциально с математическим ожиданием 3. после обслуживания на третьем устройстве изделие покидает систему. Построить имитирующую данный пример компьютерную модель на каком-либо языке программирования, предусмотрев при этом сбор статистики о времени пребывания изделия в системе и количество изделий на ленте каждого конвейера. Построить гистограмму для времени пребывания изделия в системе.
В данном примере используется нормальное и экспоненциальное распределение, математическое ожидание и среднеквадратичное отклонение.
Нормальное распределение. Генератор нормально распределенной случайной величины X можно получить по формулам:
12
Y=ІX-6І+µ X=ј, где
j=1
ј (j=1,…,12) - значение независимых случайных величин, равномерно распределенных на интервале (0, 1).
Равномерное распределение. Равномерное распределение случайной величины Х на отрезке [a,b] выражается через равномерно распределенную на отрезке [0,1] случайную величину R формулой:
X=a+(b-a)R
Экспоненциальное (показательное) распределение. Методом обратных функций можно показать, что показательное распределенная случайная величина Xсвязана со случайной величиной R, распределенной на [0,1], соотношением:
Y=1/*ln(1-R) , где – параметр показательного закона.
Математическое ожидание. Математическим ожиданием, т.е. средним значением случайной величины X называется числовая величина, вычисляемая по формуле:
+
MX= xdF(x)
-
Среднеквадратичное отклонение. Среднеквадратичным отклонением х случайной величины Х называется положительный квадратный корень из ее дисперсии:
х= Dx=DX
3. Описание метода решения.
Дискретно-событийный подход в имитационном моделировании.
Суть дискретно-событийного подхода - моделирование системы с помощью описания изменений состояния системы, происходящих в дискретные моменты времени. Момент времени, в который может измениться: состояние системы, называется моментом наступления события, а соответствующая ему логическая процедура обработки изменений состояния системы называется событием. Для построения дискретно-событийной модели системы необходимо определить события, при которых может изменяться состояние системы, а затем смоделировать процедуры, соответствующие каждому типу событий. Динамический портрет системы воспроизводится с помощью упорядоченной во времени последовательности событий, в каждом из которых, согласно логической процедуре, моделируются изменения состояния системы.
Состояние системы в дискретно-событийной модели, подобно состоянию в сетевой модели, определяется значениями переменных и атрибутов компонентов, принадлежащих различным классам. Начальное состояние системы устанавливается с помощью задания начальных значений переменных модели, генерации (при необходимости) начальных компонентов в системе, а также с помощью начального планирования событий в модели. В ходе имитации система «движется» от состояния к состоянию по мере того, как компоненты участвуют в действиях, изменяющих состояние системы. При дискретно-событийной имитации изменения состояния системы могут происходить только в начале действия, т. е. когда что-либо начинается, или в конце действия, т. е. когда что-либо завершается. Для моделирования начала и окончания действий используются события
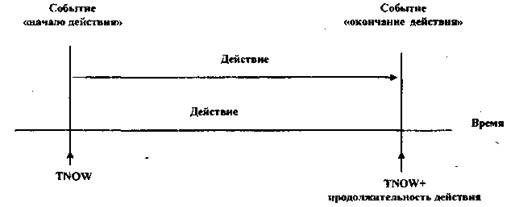
Рис. 1.1. Связь между понятиями «действие» и «событие».
Понятие события, происходящего мгновенно в определенный момент времени, в который начинается или заканчивается некоторое действие, является основополагающим. На рис. 1.1 показана связь между понятиями «действие» и «событие». Внутри события время не изменяется, а изменения состояния системы происходят только в моменты наступления событий. Поведение системы имитируется последовательностью изменений ее состояния, происходящих по мере наступления событий.
Когда происходит событие, состояние системы может быть изменено четырьмя способами:
1) изменением значений одной или нескольких переменных модели;
2) изменением количества компонентов в системе;
3) изменением значении одного или нескольких атрибутов одного компонента;
4) изменением взаимосвязей между компонентами с помощью средств оперирования с: файлами. Отметим, что возможны и такие события, при которых состояние системы не меняется.
В ходе имитации осуществляется планирование наступления событий в заданные моменты времени. События имеют атрибуты и заносятся в файл в хронологическом порядке. Например, при планировании наступления события окончания обслуживания атрибуты обслуживаемого клиента являются частью этого события, поэтому они доступны в момент его обработки. Таким образом, если компонент проходит через некоторую последовательность действий, причем завершение каждого из них отображается в соответствующем событии, то по мере обработки событий атрибуты компонента передаются через всю систему.
4. Разработка модели.
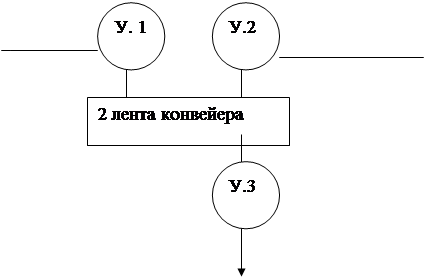
Формализованная схема.
если занято если занято
 |
 |
|
если свободно если свободно
 |
Готовая продукция
Описание формализованной схемы.
В данном примере имеется две ленты и три обслуживающихся устройства (У.1, У.2, У.3). На 1й и 2й ленте обслуживаются два обслуживающихся устройства У.1 и У.2.
Изделия поступают на первую ленту и если устройства свободны, то происходит обслуживание изделия первым или вторым устройством. А если устройства заняты, то они возвращаются на первую ленту и остаются на ней пока устройства не освободятся.
Когда устройство у первой ленты завершает обработку изделия, оно помещает его на ленту второго конвейера. Изделия поступают к третьему устройству через определенный период времени после попадания на второй конвейер. Если третье обслуживающее устройство занято, то изделие остается на ленте конвейера и через определенный период времени снова попадает к этому устройству.
После обслуживания на третьем устройстве изделие покидает систему.
Временная диаграмма.
 |
1 лента
У. 1
У. 2
2 лента
У. 3
Описание временной диаграммы.
На данном рисунке изображена временная диаграмма, иллюстрирующая работу конвейерной системы. В данной системе имеется три обслуживающих устройства, которые обслуживаются двумя лентами конвейера. Изделия поступают на первый конвейер с постоянным интервалом, равным 10 единицам времени.
Практика исследования систем обслуживания показывает, что во многих случаях удовлетворительной оказывается аппроксимация функции распределения интервалов между моментами поступления изделия в систему обслуживания экспоненциальной функцией:
 -t
-t
1-eпри t =0,
A(t)=
0 при t 0,
где – величина, обратная среднему интервалу времени между заявками.
Время обслуживания изделия распределено экспоненциально:
Методом обратных функций можно показать, что показательное распределенная случайная величина Xсвязана со случайной величиной R, распределенной на [0,1], соотношением:
Y=1/*ln(1-R) , где – параметр показательного закона.
Блок-схема
![]()
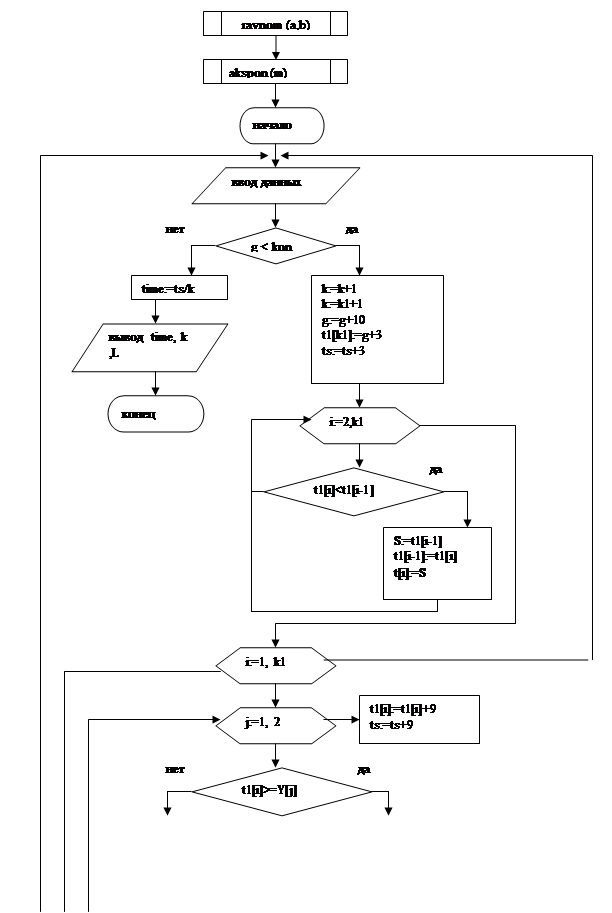
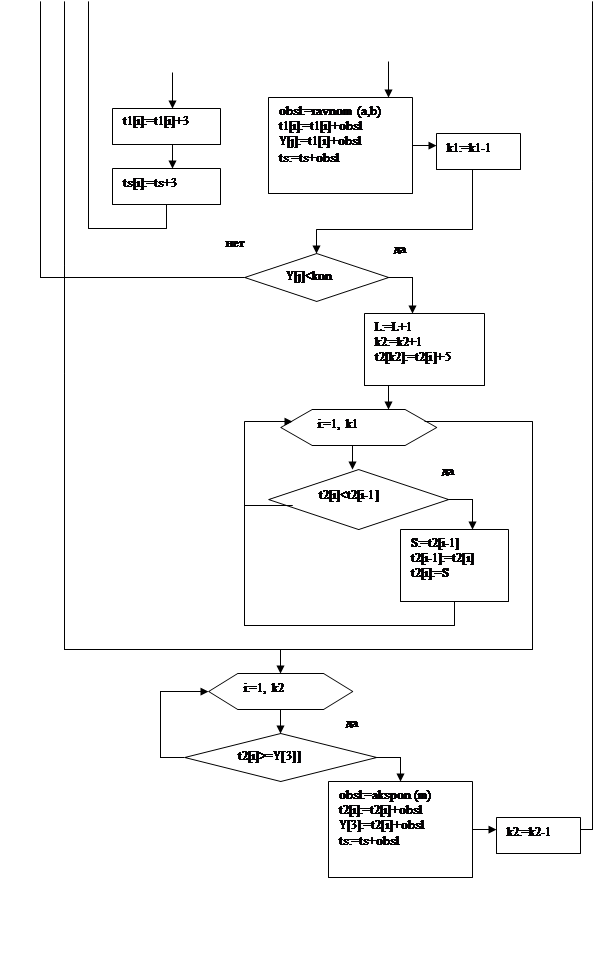
Описание переменных.
t – время поступления изделия
к – количество изделие
к1 - количество изделие на ленте первого конвейера
к2 - количество изделие на ленте второго конвейера
t[к1] – время движения изделия к1 по ленте первого конвейера
t[к2] - время движения изделия к2 по ленте первого конвейера
i – номер изделия
j – номер обслуживающего устройства
Y[j] – время работы j-го обслуживающего устройства
Y[3] – время работы 3-го обслуживающего устройства
time – среднее время пребывания изделия в системе
obsl – время обслуживания изделия
L – Количество обслужившихся изделий
rab– время начало работы
Программа.
uses crt;
label lb1;
var
g,m,rab,time,s,ts,obsl,a,b:real;
k,k1,k2,i,j,l:integer;
t1,t,y,t2:array[1..100] of real;
function akspon(m2:real):real;
var x,r:real;
begin
randomize;r:=random(1);
x:=-(1/m2)*ln(1-r);
end;
function ravnom(a,b:real):real;
var x, r:real;
begin
randomize;r:=random(1);
x:=a+(b-a)*r;
end;
Begin
CLRSCR;
g:=0; k1:=0; k2:=0;
writeln(vvedite a,b,m,rab);
read(a,b,m,rab);
lb1:if grab then begin
k:=k+1; k1:=k1+1;
g:=g+10; t1[k1]:=g+3;
ts:=ts+3;
for i:=2 to k1 do
if t1[i]t1[i-1] then begin
S:=t1[i-1];
t1[i-1]:=t1[i];
t1[i]:=S;
end;
for i:=1 to k1 do begin
for j:=1 to 2 do begin
if t1[i]=Y[j] then begin
obsl:=ravnom(a,b);
t1[i]:=t1[i]+obsl;
Y[j]:=t1[i]+obsl;
ts:=ts+obsl; k1:=k1-1;
if Y[j]rab then begin
l:=l+1; k2:=k2+1;
t2[k2]:=t1[i]+5;
end;
for i:=1 to k2 do
if t2[i]t2[i-1] then begin
S:=t2[i-1];
t2[i-1]:=t2[i];
t2[i]:=S;
end else
goto lb1; end
else
t2[i]:=t1[i]+3;
ts:=ts+3;
t1[i]:=t1[i]+9;
ts:=ts+9;end;
end;
t2[i]:=t1[i]+9;
ts:=ts+9;
end;
for i:=1 to k2 do
if t2[i]=Y[3] then begin
obsl:=akspon(m); t2[i]:=t2[i]+obsl;
Y[3]:=t2[i]+obsl;
ts:=ts+obsl; k2:=k2-1;
end else
time:=ts/k;
writeln(time=,time,k=,k,l=,l);
End.
writen (time;k,l);
end.
Верификация .
vvedite a, b, m, rab
0
1
5
8