Критерии принятия решений
СОДЕРЖАНИЕ: Министерство общего и профессионального образования Российской Федерации РЕФЕРАТ ПО ПРЕДМЕТУ ТЕОРИЯ ПРИНЯТИЯ РЕШЕНИЙ Критерии принятия решений Выполнила:Министерство общего и профессионального образования Российской Федерации
РЕФЕРАТ ПО ПРЕДМЕТУ
ТЕОРИЯ ПРИНЯТИЯ РЕШЕНИЙ
Критерии принятия решений
Выполнила:
Санкт-Петербург
2011
Содержание
Введение..................................................................................................3
1. Критерии принятия решений..............................................................6
1.1. Минимаксный критерий...................................................................6
1.2. Критерий Сэвиджа ..........................................................................7
1.3. Критерий Байеса-Лапласа. ..............................................................8
1.4. Расширенный минимаксный критерий..........................................8
1.5. Критерий произведений...................................................................9
1.6. Критерий Гермейера.......................................................................9
1.7. Критерий Гурвица...........................................................................10
1.8. Составной критерий Байеса-Лапласа минимаксный...................10
Список используемой литературы.......................................................13
Введение
Основные понятия системного анализа
Системный анализ - наука, занимающаяся проблемой принятия решения в условиях анализа большого количества информации различной природы.
Из определения следует, что целью применения системного анализа к конкретной проблеме является повышение степени обоснованности принимаемого решения, расширение множества вариантов, среди которых производится выбор, с одновременным указанием способов отбрасывания заведомо уступающим другим.
В системном анализе выделяют
· методологию;
· аппаратную реализацию;
· практические приложения.
Методология включает определения используемых понятий и принципы системного подхода.
Дадим основные определения системного анализа.
Связь - важный для целей рассмотрения обмен между элементами веществом, энергией, информацией.
Элемент - некоторый объект (материальный, энергетический, информационный), который обладает рядом важных для нас свойств, но внутреннее строение (содержание) которого безотносительно к цели рассмотрения.
Система - совокупность элементов, которая обладает следующими признаками:
· связями, которые позволяют посредством переходов по ним от элемента к элементу соединить два любых элемента совокупности;
· свойством, отличным от свойств отдельных элементов совокупности.
Практически любой объект с определенной точки зрения может быть рассмотрен как система. Вопрос состоит в том, насколько целесообразна такая точка зрения.
Большая система - система, которая включает значительное число однотипных элементов и однотипных связей. В качестве примера можно привести трубопровод. Элементами последнего будут участки между швами или опорами. Для расчетов на прочность по методу конечных элементов элементами системы считаются небольшие участки трубы, а связь имеет силовой (энергетический) характер - каждый элемент действует на соседние.
Сложная система - система, которая состоит из элементов разных типов и обладает разнородными связями между ними.
Автоматизированная система - сложная система с определяющей ролью элементов двух типов:
· в виде технических средств;
· в виде действия человека.
Для сложной системы автоматизированный режим считается более предпочтительным, чем автоматический. Например, посадка самолета выполняется при участии человека, а автопилот или бортовой компьютер используется лишь на относительно простых операциях. Типична также ситуация, когда решение, выработанное техническими средствами, утверждается к исполнению человеком.
Структура системы - расчленение системы на группы элементов с указанием связей между ними, неизменное на все время рассмотрения и дающее представление о системе в целом. Указанное расчленение может иметь материальную, функциональную, алгоритмическую или другую основу. Пример материальной структуры - структурная схема сборного моста, которая состоит из отдельных, собираемых на месте секций и указывает только эти секции и порядок их соединения. Пример функциональной структуры - деление двигателя внутреннего сгорания на системы питания, смазки, охлаждения, передачи крутящего момента. Пример алгоритмической структуры - алгоритм программного средства, указывающего последовательность действий или инструкция, которая определяет действия при отыскании неисправности технического устройства.
Структура системы может быть охарактеризована по имеющимся в ней типам связей. Простейшими из них являются последовательное, параллельное соединение и обратная связь (рис.1.1).
Декомпозиция - деление системы на части, удобное для каких-либо операций с этой системой. Примерами будут: разделение объекта на отдельно проектируемые части, зоны обслуживания; рассмотрение физического явления или математическое описание отдельно для данной части системы.
Иерархия - структура с наличием подчиненности, т.е. неравноправных связей между элементами, когда воздействие в одном из направлений оказывают гораздо большее влияние на элемент, чем в другом. Виды иерархических структур разнообразны, но важных для практики иерархических структур всего две - древовидная и ромбовидная (рис.1.2).
Древовидная структура наиболее проста для анализа и реализации. Кроме того, в ней всегда удобно выделять иерархические уровни - группы элементов, находящиеся на одинаковом удалении от верхнего элемента. Пример древовидной структуры - задача проектирования технического объекта от его основных характеристик (верхний уровень) через проектирование основных частей, функциональных систем, групп агрегатов, механизмов до уровня отдельных деталей.
Принципы системного подхода - это положения общего характера, являющиеся обобщением опыта работы человека со сложными системами. Их часто считают ядром методологии. Известно около двух десятков таких принципов, ряд из которых целесообразно рассмотреть:
· принцип конечной цели: абсолютный приоритет конечной цели;
· принцип единства: совместное рассмотрение системы как целого и как совокупности элементов;
· принцип связности: рассмотрение любой части совместно с ее связями с окружением;
· принцип модульного построения: полезно выделение модулей в системе и рассмотрение ее как совокупности модулей;
· принцип иерархии: полезно введение иерархии элементов и(или) их ранжирование;
· принцип функциональности: совместное рассмотрение структуры и функции с приоритетом функции над структурой;
· принцип развития: учет изменяемости системы, ее способности к развитию, расширению, замене частей, накапливанию информации;
· принцип децентрализации: сочетание в принимаемых решениях и управлении централизации и децентрализации;
· принцип неопределенности: учет неопределенностей и случайностей в системе.
· Критерий Байеса-Лапласа предъявляет к ситуации, в которой принимается решение, следующие требования:
· вероятность появления состояния Vj известна и не зависит от времени;
· принятое решение теоретически допускает бесконечно большое
· количество реализаций;
· допускается некоторый риск при малых числах реализаций.
В соответствии с критерием Сэвиджа в качестве оптимальной выбирается такая стратегия, при которой величина риска принимает наименьшее значение в самой неблагополучной ситуации:
![]()
Здесь величину W можно трактовать как максимальный дополнительный выигрыш, который достигается, если в состоянии Vj вместо варианта Ui выбрать другой, оптимальный для этого внешнего состояния, вариант.
Соответствующее критерию Сэвиджа правило выбора следующее: каждый элемент матрицы решений [Wij ] вычитается из наибольшего результата max Wij соответствующего столбца. Разности образуют матрицу остатков. Эта матрица пополняется столбцом наибольших разностей Wir . Выбирается тот вариант, в строке которого стоит наименьшее значение.
Согласно критерию Гурвица выбирается такая стратегия, которая занимает некоторое промежуточное положение между крайним пессимизмом и оптимизмом:
![]()
где
r - коэффициент пессимизма, выбираемый в интервале [0,1].
Правило выбора согласно этому критерию следующее: матрица решений [Wij ] дополняется столбцом, содержащим средние взвешенные наименьшего и наибольшего результатов для каждой строки (2.6). Выбирается тот вариант, в строках которого стоят наибольшие элементы Wir этого столбца.
При r =1 критерий Гурвица превращается в критерий Вальда (пессимиста), а при r =0 - в критерий азартного игрока. Отсюда ясно, какое значение имеет весовой множитель r . В технических приложениях правильно выбрать этот множитель бывает так же трудно, как правильно выбрать критерий. Поэтому чаще всего весовой множитель r =0.5 принимается в качестве средней точки зрения.
Критерий Гурвица предъявляет к ситуации, в которой принимается решение, следующие требования:
· о вероятности появления состояния Vj ничего не известно;
· с появлением состояния Vj необходимо считаться;
· реализуется лишь малое количество решений;
1.Критерии принятия решений
Критерий принятия решений - это функция, выражающая предпочтения лица, принимающего решения (ЛПР), и определяющая правило, по которому выбирается приемлемый или оптимальный вариант решения.
Всякое решений в условиях неполной информации принимается в с учетом количественных характеристик ситуаций, в которой принимаются решения. Наиболее часто принимаются следующие критерии принятия Севиджа, критерий Гурвица, критерий Ходжа-Лимона, критерий Гермейера, соответствии с решений: минимаксный критерий, критерий Байеса-Лапласа, критерий какой-либо оценочной информацией, выбор которой должен осуществляться критерий произведений, составной критерий Байеса-Лапласа минимаксный.
Эти критерии можно использовать поочередно, причем после вычисления их значений среди нескольких вариантов приходится произвольным образом выделять некоторое окончательное решение. Что позволяет, во-первых, лучше проникнуть во все внутренние связи проблемы принятия решений и, во-вторых, ослабить влияние субъективного фактора.
Классические критерии принятия решений.
1.1. Минимаксный критерий (ММ) использует оценочную функцию ZММ , соответствующую позицию крайней осторожности.
ZММ =max eirи eir=min eij.
гдеzmm — оценочная функция ММ-критерия.
Поскольку в области технических задач построение множества Е вариантовуже само по себе требует весьма значительных усилий, причем иногда возникает необходимость в их рассмотрении с различных точек зрения. Оно должно напоминать о том, что совокупность вариантов необходимо исследовать возможно более полным образом, чтобы была обеспечена оптимальность выбираемого варианта.
Правило выбора решения в соответствии с этим критерием можно интерпретировать следующим образом:
Матрица решений дополняется еще одним столбцом из наименьших результатов eir каждой строки. Выбрать надлежит те варианты Eio , в строках которых стоят наибольшие значения eir этого столбца.
Выбранные таким образом варианты полностью исключают риск. Это означает, что принимающий решение не может столкнуться с худшим результатом,чем тот, на который он ориентируется. Какие бы условия Fjни встретились, соответствующий результат не может оказаться ниже Zмм . Это свойство заставляет считать минимаксный критерий одним из фундаментальных. Поэтому в технических задачах он применяется чаще всего, как сознательно, так и неосознанно. Однако положение об отсутствии риска стоит различных потерь.
1.2. Критерий Сэвиджа.
С помощью обозначения
аij=max eij – eij – это eir=maxaij = max(max eij-eij),
формируетсяоценочнаяфункция
Zs=min eir = min [max (maxeij – eij )]
Соответствующее правило выбора теперь интерпретируется так:
Каждый элемент матрицы решений вычитается из наибольшего результата соответствующего столбца. Эти разности образуют матрицу остатков. Эта матрица пополняется столбцом наибольших разностей eir . Выбираются те решения Еio , в строках которых стоит наименьшее значение для этого столбца
и строится множество оптимальных вариантов решения
![]()
Для понимания этого критерия определяемую соотношением величину aij = max eij - eij можно трактовать как максимальный дополнительный выигрыш, который достигается, если в состоянии Fj вместо варианта Ei выбрать другой, оптимальный для этого внешнего состояния вариант. Мы можем, однако, интерпретировать aij и как потери (штрафы), возникающие в состоянии Fi при замене оптимального для него варианта на вариант Ei . Тогда определяемая соотношением величина eir представляет собой — при интерпретации аij в качестве потерь—максимальные возможные (по всем внешним состояниям Fj , j==1, ..., n) потери в случае выбора варианта Ei . Эти максимально возможные потери минимизируются за счет выбора подходящего варианта Ei .
Соответствующее S-критерию правило выбора теперь интерпретируется так:
каждый элемент матрицы решений ||eij || вычитается из наибольшего результата max eij соответствующего столбца.
Разности aij образуют матрицу остатков ||aij || Эта матрица пополняется столбцом наибольших разностей eir . Выбираются те варианты Eio , в строках которых стоит наименьшее для этого столбца значение.
По выражению оценивается значение результатов тех состояний, которые, вследствие выбора соответствующего распределения вероятностей, оказывают одинаковое влияние на решение, с точки зрения результатов матрицы ||eij || S-критерий связан с риском, однако, с позиций матрицы ||aij || он от риска свободен.
1.3. Критерий Байеса-Лапласа.
Этот критерий учитывает каждое из возможных следствий. Пусть qj – вероятность появления внешнего состояния Fj , тогда для этого критерия оценочная функция запишется так:
ZBL =max eir, eir= eijqj.
Тогда правило выбора будет записано так:
Матрица решений дополняется еще одним столбцом, содержащим математическое ожидание значений каждой из строк. Выбираются те варианты Eio , в строках которых стоит наибольшее значение eir этого столбца.
1.4. Расширенный минимаксный критерий .
В нем используются простейшие понятия теории вероятностей, а также, в известном смысле, теории игр. В технических приложениях этот критерий до сегоднешнего времени применяется мало.
Основным здесь является предположение о том, что каждому из n возможных внешних состояний Fj приписана вероятность его появления : 0 q1.
Тогда расширенный ММ-критерий формулируется следующим образом:
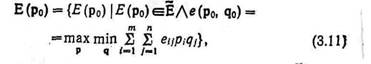
где р—вероятностный вектор для Ei , a q—вероятностный вектор для Fj .
Таким образом, расширенный ММ-критерий задается целью найти наивыгоднейшее распределение Ei вероятностей на множестве вариантов, когда в многократно воспроизводящейся ситуации ничего не известно о вероятностях состояний Fj . Поэтому предполагается, что Fj распределены наименее выгодным образом.
1.5.Критерий произведений.
С самого начала этот критерий ориентирован на величины выигрышей, то есть на положительные значения величины е
Определим оценочную функцию:
Zp=max eir.
Привило выбора в этом случае формулируется так:
Матрица решений дополняется новым столбцом, содержащим произведения всех результатов каждой строки. Выбираются те варианты Еiо, в строках которых находятся наибольшие значения этого столбца.
Применение этого критерия обусловлено следующими обстоятельствами:
Вероятности появления состояний Fj неизвестны; с появлением каждого из состояний Fj по отдельности необходимо считаться; критерий применим при малом числе реализаций решения; некоторый риск допускается.
Как уже упоминалось, этот критерий приспособлен в первую очередь для случаев, когда все eij положительны. Если указанное условие нарушается, а этот критерий приходится применять и в этом случае, то следует выполнить некоторый сдвиг eij+a с некоторой константой а | min eij |. Разумеется, результат применения критерия существенно зависит от этого значения а. На практике в качестве значения, а охотно используют величину | min eij | + 1. Если же никакая константа не может быть признана имеющей смысл, то к таким проблемам этот критерий не применим.
Выбор оптимального решения согласно критерию произведений оказывается значительно минее пессимистическим, чем, например, выбор в соответствии с минимаксным критерием. В результате применения критерия произведений происходит некоторое выравнивание между большими и малыми значениями eij, и, устанавливая оптимальный вариант решения с помощью этого критерия, мы можем при фиксированных состояниях Fj получить большую выгоду, чем при использовании минимаксного критерия, но при этом должна учитываться возможность появления и худших результатов. Следует отметить, что при использовании этого критерия ни число реализаций, ни информация о распределении вероятностей не принимаются во внимание.
1.6.Критерий Гермейера .
Отправляясь от подхода Гермейера к отысканию эффективных и пригодных к компромиссу решений в области полиоптимизации – т.е. всех решений, которые не считаются заведомо худшими, чем другие, - можно предположить еще один критерий, обладающий в некотором отношении определенной эластичностью. Он с самого начала ориентирован на величины потерь, т.е. на отрицательные значения eij.
В качестве оценочной функции выступает
ZG =max eij
Поскольку в хозяйственных задачах преимущественно имеют дело с ценами и затратами, условие eij0 обычно выполняется. В случае же, когда среди величин eij встречаются и положительные значения, можно перейти к строго отрицательным значениям с помощью преобразования eij - а при подходящим образом подобранном а0.
Правило выбора согласно критерию Гермейера формулируется следующим образом:
Матрица решений дополняется еще одним столбцом, содержащим в каждой строке наименьшее произведение имеющегося в ней результата на вероятность соответствующего состояния Fj. Выбираются те решения Еiо, в строках которых находится наибольшее значение eir этого столбца.
1.7.Критерий Гурвица .
Стараясь занять наиболее уравновешенную позицию, Гурвиц предложил критерий, оценочная функция которого находится где-то между точками зрения предельного оптимизма и крайнего пессимизма:
ZHW=maxeir.
Правило выбора согласно HW-критерию формулируется так:
Матрица решений дополняется столбцом, содержащим средние взвешенные наибольшего и наименьшего результатов для каждой строки. Выбираются те варианты Eio, в строках которых стоят наибольшие элементы eij этого столбца. В технических приложениях правильно выбрать множитель с бывает так же трудно, как правильно выбрать критерий. Вряд ли возможно найти количественную характеристику для тех долей оптимизма и пессимизма, которые присутствуют при принятии решения. Поэтому чаще всего весовой множитель с=0,5 без возражений принимается в качестве некоторой «средней» точки зрения. При обосновании выбора применяют обратный порядок действий. Для приглянувшегося решения вычисляется весовой множитель с, и он интерпретируется как показатель соотношения оптимизма и пессимизма. Таким образом, позиция исходя из которых принимаются решения, можно рассортировать, по крайней мере, задним числом.
Этот критерий предъявляет к ситуации, в которой принимается решение, следующие требования:
О вероятностях появления состояния Fj ничего не известно; с появлением состояния Fj необходимо считаться; реализуется лишь малое количество решений; допускается некоторый риск
1.8. Составной критерий Байеса-Лапласа минимаксный.
Стремление получить критерии, которые бы лучше приспосабливались к имеющейся ситуации, чем все до сих пор рассмотренные, привело к построению так называемых составных критериев.
Исходным для построенного был BL-критерий Вследствие того, что распределение q=(q 1 , ..., qn ) устанавливается эмпирически и потому известно неточно, происходит, с одной стороны, ослабление критерия, а с другой, напротив, с помощью заданных границ для риска и посредством MM-Kритерня обеспечивается соответствующая свобода действий. Точные формулировки состоят в следующем.
Зафиксируем прежде всего задаваемое ММ-критерием опорное значение:
![]()
где i 0 и j0 —оптимизирующие индексы для рассматриваемых вариантов решений и, соответственно, состояний.
Посредством некоторого заданного или выбираемого уровня допустимого риска E доп 0 определим некоторое множество согласия, являющееся подмножеством множества индексов {1, ... ..., т}:
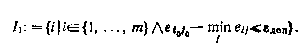
Величина E i :=ei 0 j 0 - minj eij для всех i I1 характеризует наибольшие возможные потери в сравнении со значением ei 0 j 0 , задаваемым ММ-критерием. С другой стороны, в результате такого снижения открываются и возможности для увеличения выигрыша по сравнению с тем, который обеспечивается ММ-критерием. Поэтому мы рассматриваем также (опять-таки как подмножество множества {1, ..., m}) некоторое выигрышное множество
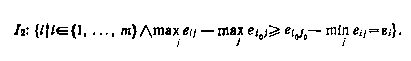
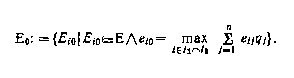 |
Тогда в множество-пересечение I1 I2 мы соберем только такие варианты решений, для которых, с одной стороны, в определенных состояниях могут иметь место потери по сравнению с состоянием, задаваемым ММ-критерием, но зато в других состояниях имеется по меньшей мере такой же прирост выигрыша. Теперь оптимальными в смысле BL (ММ)-критерия будут решения
Правило выбора для этого критерия формулируется следующим образом.
Матрица решений ||еij || дополняется еще тремя столбцами. В первом из них записываются математические ожидания каждой из строк, во втором—разности между опорным значением ei 0 j 0 = ZMM и наименьшим значением minj (еij ) соответствующей строки. В третьем столбце помещаются разности между наибольшим значением maxj еij каждой строки и наибольшим значением maxei 0 j той строки, в которой находится значение ei 0 j 0 . Выбираются те варианты Ei0 строки которых (при соблюдении приводимых ниже соотношений между элементами второго и третьего столбцов) дают наибольшее математическое ожидание. А именно, соответствующее значение ei 0 j 0 – minj еij из второго столбца должно быть меньше или равно некоторому заранее заданному уровню риска доп . Значение же из третьего столбца должно быть больше значения из второго столбца.
Применение этого критерия обусловлено следующими признаками ситуации, в которой принимается решение:
· вероятности появления состояний FJ неизвестны, однако имеется некоторая априорная информация в пользу какого-либо определенного распределения;
· необходимо считаться с появлениями различных состояний как по отдельности, так и в комплексе;
· допускается ограниченный риск;
· принятое решение реализуется один раз или многократно.
Таким образом, спектр применимости теории распространяется далеко за пределы предыдущих критериев. Особо следует подчеркнуть, что действие новых критериев остается вполне обозримым, хотя функция распределения может играть лишь подчиненную роль.
BL (ММ)-критерий хорошо приспособлен для построения практических решений прежде всего в области техники и может считаться достаточно надежным. Однако задание границы риска доп и, соответственно, оценок риска i не учитывает ни число применений решения, ни иную подобную информацию. Влияние субъективного фактора хотя и ослаблено, но не исключено полностью;
Условие maxj еij – maxj еi0 j = i существенно в тех случаях, когда решение реализуется только один или малое число раз. В этих случаях недостаточно ориентироваться на риск, связанный лишь с невыгодными внешними состояниями и средними значениями. Из-за этого, правда, можно понести некоторые потери в удачных внешних состояниях. При большом числе реализации это условие перестает быть таким уж важным. Оно даже допускает разумные альтернативы.
Список литературы
Бинкин Б.А., Черняк В.И. Эффективность управления: наука и практика. М.: Наука, 1982. 143 с.
Мушик З., Мюллер П. Методы принятия технических решений. - М.: Мир, 1990. - 208с
Могилевский В.Д.Методология систем: вербальный подход. / М., Экономика, 1999. 251 с.
Саати Т., Кернс К. Аналитическое планирование. Организация систем. / М. Радио и связь. 1991.