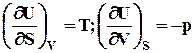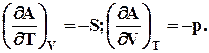Курс лекций по физической химии Учебно-методическое пособие
СОДЕРЖАНИЕ: Физическая химия изучает общие вопросы химического строения веще-ства, общие количественные закономерности химического равновесия и химических процессов, а также физических явлений, которые их сопро-вождаютФедеральное агентство по образованию
Московская государственная академия
тонкой химической технологии им. М.В. Ломоносова
Кафедра физической химии
Курс лекций по физической химии
Учебно–методическое пособие
Москва, 2006
Лекция № 1
1. Предмет, структура и методы физической химии.
1.1. Физическая химия изучает общие вопросы химического строения веще-ства, общие количественные закономерности химического равновесия и химических процессов, а также физических явлений, которые их сопро-вождают.
1.1.1. Термин физическая химия введен М. В. Ломоносовым. «Физическая химия - наука, которая должна на основе положений и опытов физических объяснить причину того, что происходит через химические операции в сложных телах.» Т.е. ФХ изучает связь между физическими и хими-ческими явлениями, физические процессы, которыми сопровождаются химические реакции.
1.1.2. Физическая химия – это теоретическая химия, которая рассматривает общие законы, определяющие химические процессы, а именно направление химических реакций, условия равновесия, протекание во времени, влияние различных факторов на химические реакции. ФХ дает математическое описание химических процессов, что позволяет перевести изучение химических явлений на компьютерную основу.
1.1.3. Физическая химия – основа химической технологии, она позволяет оптимизировать протекание химических реакций, сделать их более экологически безопасными.
1.1.4. Физическая химия изучает строение веществ, связь между структурой и физико-химическими свойствами веществ, т.е. дает основу материаловедения, науки, которая определяет технический прогресс.
1.1.5. Физическая химия - основа аналитической химии, т.к. она имеет дело с методами изучения структуры вещества, а, следовательно, его идентификации физическими методами.
1.2. Основные разделы физической химии
1.2.1. Химическая термодинамика – как часть научной дисциплины общей термодинамики – исследует условия равновесия в физико-химических процессах и химических реакциях..
1.2.2. Строение вещества – теории химической связи и расчетные и экспериментальные методы изучения строения.
1.2.3. Химическая кинетика – протекание во времени и механизмы химических реакций
1.2.4. Электрохимия
1.2.5. Промежуточные, объединяющие разделы :
Статистическая термодинамика
Теория реакционной способности
Термодинамика необратимых процессов
Электрохимическая кинетика
2. Основные понятия химической термодинамики
2.1. Термодинамические системы .
2.1.1. Термодинамическая система – это часть материального мира, отделенная от окружающей среды реальными или воображаемыми границами и являющаяся объектом исследования. Окружающая среда значительно больше по объему, и поэтому изменения в ней незначительны по сравнению с изменением состояния системы. В отличие от механических систем, которые состоят из одного или нескольких тел, термодинамическая система содержит очень большое число частиц, что порождает совершенно новые свойства и требует иных подходов к описанию состояния и поведения таких систем. Термодинамическая система представляет собой макроскопический объект .
2.1.2. Классификация термодинамических систем
2.1.2.1. По составу
Термодинамическая система состоит из компонентов. Компонент - это вещество, которое может быть выделено из системы и существовать вне ее, т.е. компоненты – это независимые вещества.
2.1.2.1.1. Однокомпонентные.
2.1.2.1.2. Двухкомпонентные, или бинарные.
2.1.2.1.3. Трехкомпонентные – тройные.
2.1.2.1.4. Многокомпонентные.
2.1.2.2. По фазовому составу – гомогенные и гетерогенные
2.1.2.2.1. Гомогенные системы имеют одинаковые макроскопические свойства в любой точке системы, прежде всего температуру, давление, концентрацию, а также многие другие, например, показатель преломления, диэлектрическую проницаемость, кристаллическую структуру и др. Гомогенные системы состоят из одной фазы.
Фаза – это однородная часть системы, отделенная от других фаз поверхностью раздела и характеризующаяся своим уравнением состояния. Фаза и агрегатное состояние – перекрывающиеся, но не идентичные понятия. Агрегатных состояний только 4 , фаз может быть гораздо больше.
2.1.2.2.2. Гетерогенные системы состоят минимум из двух фаз.
2.1.2.3. По типам связей с окружающей средой (по возможностям обмена с окружающей средой)
2.1.2.3.1. Изолированная система не обменивается с окружающей ни энергией, ни веществом. Это идеализированная система, которую, в принципе нельзя экспериментально изучать.
2.1.2.3.2. Закрытая система может обмениваться с окружающей средой энергией, но не обменивается веществом.
2.1.2.3.3. Открытая система обменивается и энергией, и веществом
2.2. Состояние ТДС
2.2.1.Определение.
Состояние ТДС – это совокупность всех ее измеримых макроскопических свойств, имеющих, следовательно, количественное выражение. Макроскопический характер свойств означает, что их можно приписать только к системе в целом, а не отдельным частицам, которые составляют ТДС ( Т, р, V, c, U, nk ). Количественные характеристики состояния связаны между собой. Поэтому существует минимальный набор характеристик системы, называемых параметрами , задание которых позволяет полностью описать свойства системы. Количество этих параметров зависит от типа системы. В простейшем случае для закрытой гомогенной газовой системы в состоянии равновесия достаточно задать только 2 параметра. Для открытой системы кроме этих 2 характеристик системы требуется задать число молей каждого компонента.
2.2.2. Равновесие
Классическая термодинамика обычно ограничивается рассмотрением равновесных состояний ТДС. Равновесие - это такое состояние, к которому самопроизвольно приходит ТДС, и в котором она может существовать бесконечно долго в отсутствие внешних воздействий. Для определения равновесного состояния всегда требуется меньшее количество параметров, чем для неравновесных систем.
2.2.3. Уравнение со c тояния связывает параметры состояния и относится к фазе. Общий вид его f ( p , V , T ) = 0. Простейший вид уравнения состояния имеет идеальный газ pV = nRT , ( 1.1)
где R = 8.314 Дж/(моль.К) = 1,987 кал/(моль.К) = 0,082 л.атм/(моль.К) .
[p] = Па, 1атм = 1,013*105 Па = 760 мм рт.ст.,
[V ] = м3 , 1 м3 = 103 л,
[T] = К,
[n] = моль, N = 6.02*1023 моль-1 = 6,02*1026 кмоль-1 .
2.2.4. Функции сост ояния – это характеристики системы, которые зависят только от параметров состояния, но не зависят от способа его достижения.
![]()
 F
(x,y), например, F
(V,T)
F
(x,y), например, F
(V,T)
![]() = 0, dF
– полный дифференциал
= 0, dF
– полный дифференциал
![]() dF
=
dF
= 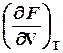 dV
+
dV
+ 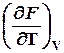 dT
, (1.2)
dT
, (1.2)
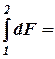 F
2
–
F
1
=
D
F
. (1.3)
F
2
–
F
1
=
D
F
. (1.3)
Изменение функции состояния не зависит от пути перехода, а определяется только начальным и конечным состоянием, D F – всегда разность между конечным (F 2 ) и начальным (F 1 ) состоянием.
2.2.5. Классификация параметров и функций состояния
2.2.5.1. Интенсивные свойства при контакте двух систем выравниваются
(температура, давление, поверхностное натяжение, электрический потен-циал) Y ’ 1 Y ’’1
Y 2 = Y ’2 = Y ’’2 , Y ’ 1 Y 2 Y ’’1. (1.4)
2.2.5.2. Экстенсивные свойства при объединении (контакте) двух систем складываются ( Объем, число молей, энергия, теплоемкость и т. д.)
X = X ’ + X ’’ (1.5)
Экстенсивные свойства зависят от массы. Чтобы описать экстенсивные свойства, их относят к определенному количеству вещества, например,
к одному молю X / n = X – мольные величины ,
к единице массы X / m = X уд . – удельные величины ,
к единице объема X / V = r – плотности .
Мольные величины не зависят от массы, поэтому их иногда относят к интенсивным свойствам, он они не обладают главной особенностью интенсивных величин – они не выравниваются при контакте.
2.3. Термодинамический процесс - изменение состояния системы при взаимодействии с окружающей средой.
2.3.1. Классификация термодинамических процессов
2.3.1.1. Циклические и нециклические
2.3.1.2. Обратимые и необратимые
2.3.1.2.1. Необратимые – это реальные процессы в термодинамических системах.
2.3.1.2.2. Обратимые – это идеализированные процессы, которые проходят в прямом и обратном направлении через одни и те же промежуточные состояния, и после завершения цикла ни в системе, ни в окружающей среде не наблюдается никаких изменений. Обратимые процессы называют часто равновесными , так как в каждый момент промежуточного состояния внешние и внутренние силы должны быть почти скомпенсированы (последнее характерно для состояния равновесия), т.е. они должны отличаться на бесконечно малую величину. Такой процесс происходит бесконечно медленно, поэтому время не учитывается в термодинамике обратимых процессов, и их также называют квазистатическими. Пример – обратимое изотермическое расширение идеального газа. В обратимом процессе работа, полученная в прямом направлении должна быть численно равна работе, затраченной в обратном процессе. По сравнению с необратимыми процессами обратимый процесс дает возможность получить максимальную работу.
2.3.2. Теплота и работа – способы обмена энергией между ТДС и окружа-ющей средой. Теплота и работа характеристики процесса, они не являются функциями состояния
2.3.2.1. Теплота – форма обмена энергией на микроскопическом уровне, т.е. в форме изменения хаотического движения молекул. Теплота считается положительной, если она подводится к системе.
2.3.2.2. Работа - форма обмена энергией на макроскопическом уровне, когда происходят направленное перемещение объекта. Работа считается положительной, если ее совершает система против внешних сил.
В зависимости от характера объекта различают разные виды работы:
2.3.2.2.1. Механическая - перемещение тела
d W мех = - F ех dl . (1.6)
Работа – скалярное произведение 2-х векторов силы и перемещения, т.е.
| d W мех | = F dl cos . Если направление внешней силы противоположно перемещению, совершаемому внутренними силами, то cos 0.
2.3.2.2.2. Работа расширения (чаще всего рассматривается расширение газа)
d W = - рех dV
В обратимом процессе pe х ~ - pin , поэтому обычно пишут, что
d W = р dV , (1.7)
Однако нужно иметь в виду, что это выражение справедливо только для обратимого протекания процесса, а в случае необратимого характера последнего pin - pe х, а работа d W необр. р dV
2.3.2.2.3. Электрическая – перемещение электрических зарядов
d W эл = - j dq , (1.8)
где j - электрический потенциал.
2.3.2.2.4. Поверхностная – изменение поверхности,
d W поверхн. = - s dS , (1.9)
где s - поверхностное натяжение.
2.3.2.2.5. Общее выражение для работы
d W = - Ydx , (1.10)
Y – обобщенная сила, dx - обобщенная координата, таким образом работа может рассматриваться как произведение интенсивного фактора на изменение экстенсивного.
2.3.2.2.6. Все виды работы, кроме работы расширения, называются полезной работой ( d W ’ ).
d W = р dV + d W’
2.3.2.2.7. По аналогии можно ввести понятие химической работы, когда направленно перемещается k -ое химическое вещество, nk – экстенсивное свойство, при этом интенсивный параметр m k называется химическим потенциалом k -ого вещества
d W хим = - S m k dnk . (1.11)
2.3.3. Нулевой закон термодинамики . Сформулирован позже первого и вто-рого, но по логике построения постулатов термодинамики он должен предшествовать им. Если две системы находятся в тепловом равновесии с третьей, то они находятся и в тепловом равновесии между собой.
ТА = ТВ ; ТА = ТС ТВ = ТС .
Таким образом, ответственным за тепловое равновесие является интенсивный параметр - температура. Поэтому можно процессы теплообмена также представить в виде аналогичной по структуре формулой
d Q = TdS , (1.12)
где экстенсивное свойство называется энтропией, а знак + соответствует передаче энергии системе в обратимом тепловом процессе.
Лекция №2
3. Первый закон термодинамики
3.1. Содержание первого закона термодинамики
3.1.1. Первый закон термодинамики является частным случаем закона сохранения энергии. Эмпирический закон Майер (1842), Джоуль (1842), Гесс (1840), Гельмгольц (1847). Энергия не создается и не уничтожается, а только переходит из одной формы в другую. Невозможен вечный двигатель 1-го рода, который работал бы без подвода энергии. Эквивалентность теплоты и работы.
3.1.2. Внутренняя энергия как функция состояния системы
Циклический процесс Нециклический процесс (12)
p 1 V 1 , T 1 p 1 V 1 , T 1


Q 1 W 1 Q 2 W 2
![]() p
2
V
2
,
T
2
p
2
V
2
,
T
2
Q = W Q 1 + Q 2 = W 1 + W 2
Q 1 – W 1 = -( Q 2 – W 2 )
Разность между теплотой и работой при заданных начальных и конечных параметрах системы является величиной постоянной и не зависит от пути процесса, т.е. представляет собой функцию состояния системы. Клаузиус назвал ее внутренней энергией .
D
U
=
Q
–
W
=
U
2
–
U
1
; ![]() .
.
Или в дифференциальной форме dU = d Q - d W
Внутренняя энергия – это сумма различных видов энергии частиц, составляющих систему, т.е. она включает кинетическую и потенциальную энергию частиц, но не включает кинетической энергии системы.
3.1.3. Математическое выражение и формулировка 1-го закона
Q = D U + W (2.1)
| Тепло, подведенное к системе, идет на изменение внутренней энергии системы и совершение системой работы против внешних сил. |
d Q = dU + d W = dU + pdV + d W’ (2.2)
Классическая термодинамика не дает способов расчета и измерения внутренней энергии, а только ее изменение.
3.2. Применение 1-го закона к простейшим системам
3.2.1. Изолированная система
Q = 0, W = 0, D U = 0.
Внутренняя энергия изолированной системы постоянна .
3.2.2. Изохорный процесс V = const .
3.2.2.1. Теплота изохорного процесса
Если d W ’ = 0, pdV = d W расширения = 0. W расширения = 0.
d Qv = dU ; Qv = D U (2.3)
В отсутствие полезной работы изменение внутренней энергии равно теплоте изохорного процесса . Это утверждение дает способ экспериментального измерения для изменения внутренней энергии.
3.2.2.2. Изохорное нагревание
d
Qv
=
n
Cv
dT
=
dUv
:
n
dUV
=
Cv
dT
Cv
=
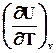 ,
(2.4)
,
(2.4)
где![]() Cv
– мольная теплоемкость системы при постоянном объеме.
Cv
– мольная теплоемкость системы при постоянном объеме.
d Q = m c уд dT
3.2.3. Изобарный процесс p = const
3.2.3.1. Работа изобарного процесса
d
W
= ![]() pdV
=
p
(
V
2
–
V
1
) =
p
D
V
(2.5)
pdV
=
p
(
V
2
–
V
1
) =
p
D
V
(2.5)
3.2.3.2. Теплота изобарного процесса
Qp = D U + p D V = ( U 2 + pV 2 ) – ( U 1 + pV 1 ) = H 2 – H 1 = D H
Qp = D H . (2.6)
Функция, стоящая в скобках называется энтальпией. Таким образом, можно сделать вывод: в отсутствие полезной работы теплота изобарного процесса равна изменению энтальпии
3.2.3.3. Энтальпия – функция состояния
Н
![]() U
+
pV
(2.7)
U
+
pV
(2.7)
В энтальпию входит внутренняя энергия (функция состояния) и произведение параметров, поэтому она также представляет собой функцию состояния, т.е. ее изменение не зависит от пути процесса.
Полный дифференциал энтальпии dH = dU + pdV + Vdp .
При р = const dH = dU + pdV = dQp .
3.2.3.4. Изобарическое нагревание
d
Qp
= n Cp
dT = dH, Cp
dT = dH
Cp
=  ,
(2.8)
,
(2.8)
где C р – мольная теплоемкость системы при постоянном давлении.
3.2.4. Изотермический процесс Т =const
3.2.4.1.Изотермическое расширение идеального газа
U = f ( T ). dU Т = 0
d Q = d W расшир. = pdV;
Q = W = ![]() =
= 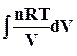 = nRT ln
= nRT ln![]() = nRT ln
= nRT ln ![]() (2.9)
(2.9)
3.2.5. Адиабатический процесс
Q = 0; d Q = 0; 0 = dU + d W расшир ;
d W расшир = - dU; W = - D U . (2.10)
Работа совершается за счет убыли внутренней энергии, например, за счет охлаждения системы
dU
=
n
Cv
dT
; W = -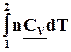 = -nCv
D
T,
если Cv
= с
onst
.
= -nCv
D
T,
если Cv
= с
onst
.
Если над системой совершается работа (сжатие, пропускание электрического тока, введение новых веществ), то внутренняя энергия системы увеличивается.
4. Термохимия
4.1. Предмет термохимии
Термохимия занимается тепловыми эффектами, сопровождающими химические и физико-химические процессы, т.е. измерениями теплоты, которая выделяется или поглощается в химических реакциях, фазовых переходах или образовании и разбавлении растворов.
4.2. Понятие теплоты химической реакции
4.2.1. Стехиометрическое уравнение химической реакции и химическая переменная.
Обычная запись уравнения химической реакции
n A A + n B B = n C C + n D D ,
или в общем виде,
0 = ![]() ,
,
где n k – стехиометрический коэффициент с учетом знака : для реагентов он отрицателен, а для продуктов положителен. Это очень удобно для обработки на компьютере. Cтехиометрическое уравнение связывает изменения чисел молей всех веществ, участвующих в реакции
3H2 + N2 = 2NH3
nk -3 -1 2
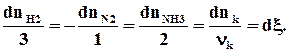
- называется химической переменной, степенью превращения, глубиной протекания реакции, координатой реакции или пробегом и является важнейшей характеристикой протекания реакции в закрытой системе, так как все изменения количества различных веществ могут быть описаны изменением одного этого внутреннего параметра. С помощью него легко составить уравнения материального баланса в закрытой системе с химической реакцией:
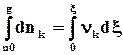
![]() nk
=
nk
о
+
n
k
x
,
(2.11)
nk
=
nk
о
+
n
k
x
,
(2.11)
где nk о и nk - количество молей k-го вещества в начальный момент реакции и на любом ее этапе соответственно.
4.2.2. Теплоты химических реакций и их связь с изменением термодина-мических функций.
4.2.2.1. Теплота при постоянном объеме 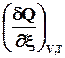
Теплотой химической реакции называют количество тепла, которое выделяется(–) или поглощается(+) за один пробег химической реакции (т.е. при полном превращении реагентов в продукты в мольных количествах, соответствующих стехиометрическим коэффициентам), при постоянном объеме, постоянной температуре и отсутствии полезной работы.
Если W
’ = 0, то
U
=
f
(
T
,
V
,
);
Qv
=
D
U
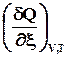 =
= 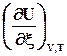 . (2.12)
. (2.12)
4.2.2.2. Теплота при постоянном давлении. 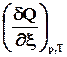
Аналогичные рассуждения приводят к выражению теплоты реакции при постоянном давлении через изменение энтальпии
Q
р
= D
Н
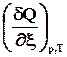 =
=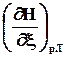 ,
при р=const, T=const, W’ = 0, x = 1. (2.13)
,
при р=const, T=const, W’ = 0, x = 1. (2.13)
4.3. Закон Гесса (1836)
4.3.1. Формулировка
Теплота реакции не зависит от пути протекания процесса, т.е. промежуточных химических стадий, через которые он проходит, а только от начального и конечного состояния веществ. Закон Гесса вкладывает дополнительный смысл в стехиометрическое уравнение реакции, а именно, что каждому веществу соответствует определенный уровень энергии и разность между этими уровнями определяет количество тепла, выделяемое или поглощаемое в химических реакциях. Можно сказать, что вещества образуют потенциальное поле, в котором переходы не зависят от пути процесса.
4.3.2. Расчет изменеия термодинамических функций в химических реакциях
По закону Гесса теплоту реакции можно представить в виде суммы изменения внутренней энергии всех веществ, участвующих в реакции
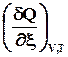 =
=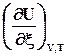 =
= 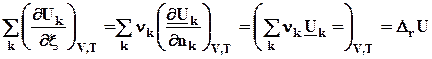
(2.14)
Оператор D r означает действие над любой функцией состояния, сводя-щееся к суммированию мольных значений этой функции для реагентов и продкутов химической реакции, умноженных на соответствующий стехи-ометрический коэффициент. Результат действия оператора D r на функцию выражает изменение данной фунции в химической реакции. В старых учебниках, в которых не используется знаки стехиометрических коэффициентов для различения реагентов и продуктов, последняя формула выглядит более громоздко
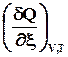 =
D
r
U
=
=
D
r
U
=
![]()
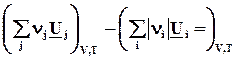 , (2.15)
, (2.15)
где индекс i относится к реагентам, а индекс j - к продуктам.
| Qv = D r U, при V=const, T = const, W’ = 0, x = 1. |
При постоянном давлении теплота химической реакции будет выражаться через действие оператора D r на энтальпию системы
Q
р
= 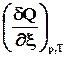 = D
r
Н
=
= D
r
Н
=
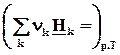 =
=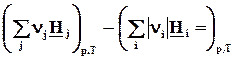 (2.16)
(2.16)
при р =const, T = const, W’ = 0, x = 1.
4.3.3. Классификация реакции по знаку теплового эффекта
D r U = Qv 0
D r Н = Q р 0 реакция эндотермическая
D r U = Qv 0
D r Н = Q р 0 реакция экзотермическая
4.3.4. Связь Q р и Qv в химических реакциях
D r Н = D r U + p D r V
В химических реакциях объем изменяется, если изменяется число молей газообразных веществ
p D r V = D r n газ RT .
При расчете на один пробег изменение числа молей газообразных ве-ществ равно алгебраической сумме стехиометрических коэффициентов этих веществ
D
r
n
газ
=
![]() газ
=(
газ
=(![]() )газ
=
D
n
k
газ
)газ
=
D
n
k
газ
D r Н = D r U + D r n k газ RT (2.17)
Пример: 1/2N2 + 3/2 H2 = NH3 D r H = -46, 19 кДж/моль = Qp
n k -1/2 -3/2 1 Dn = -1
QV = Qp + RT = -46190 + 8,314 298 = -43710 Дж/моль = - 43, 71 кДж.моль
Лекция № 3
4.3.5. Применение закона Гесса. Закон Гесса позволяет комбинировать стехиометрические уравнения, вкладывая в них термохимический смысл. Любые линейные комбинации с одинаковыми общими уравнениями имеют один и тот же тепловой эффект. Это позволяет легко определять теплоты реакций, которые трудно экспериментально провести до конца в соответствие с требованиями
H2 + O2 = H2 O2 D r H -?
+1 H2 + 1/2 O2 = H2 O D r H 1 = -285.8 кДж/моль
–1 H2 O2 = H2 O + 1/2O 2 D r H 2 = -98,7 кДж/моль
H2 + O2 = H2 O2
Подбираем коэффициенты линейной комбинации уравнений реакций, теп-лоты которых известны, чтобы в сумме получалось заданное уравнение. С такими же коэффициенты данные теплоты войдут в искомую теплоту.
D r H = D r H 1 - D r H 2 = -285,8 – (-98,7) = -187,1 Кж/моль
Энергетическая диаграмма – графическое изображение уровней реаги-рующих веществ – позволяет наглядно представить эти процессы и нахо-
________________ H 2 + O 2 дить любые неизвестные теплоты по
![]()
![]() имеющимся данным путем составле-
имеющимся данным путем составле-
-187.1 ния циклов, суммарная теплота кото-
рых равна 0.
![]()
![]() -285.8 H
2
O
2
-285.8 H
2
O
2
-98.7
![]() H
2
O
+ 1/2
O
2
H
2
O
+ 1/2
O
2
4.4. Следствия из закона Гесса
4.4.1. Первое следствие .
4.4.1.1. Понятие стандартной теплоты образования вещества
Согласно 1-ому закону термодинамики невозможно измерить абсолютное значение энергии, а только ее изменение. Поэтому нужно выбрать для различных веществ условный нуль, относительно которого определяются изменения внутренней энергии. За такой уровень отсчета приняты состояния простых веществ при стандартных условиях. Простые вещества образованы из атомов одного элемента. Если элемент существует в нескольких простых формах, то выбирается наиболее устойчивая модификация H 2(газ) , O 2 (газ) , N 2(газ) , Ar (газ) , C графит , S (ромб) , Br 2(ж)
Стандартная теплота образования – это тепловой эффект реакции образования вещества из простых веществ в стандартных состояниях. Обозначается D f H или D f U , для простых веществ D f H = D f U= 0 .
Пример,
C граф. + 1/2 O 2 + 3 H2 = C2 H5 OH(жидк.) ; D r H = D f H
4.4.1.2. Стандартное состояние – наиболее устойчивая форма чистого вещества, для газов – давление 1 атмосфера и газ должен обладать свойствами идеального газа, т.е. для него справедливо уравнение Менделеева-Клапейрона, конденсированные фазы находятся в равновесии со своим паром. Температура не входит в понятие стандартного состояния. Оно возможно при любой температуре. В справочниках теплоты образования приводятся при температуре 298,15 К, но это специально оговаривается D f H 298 .
4.4.1.3. 1-ое следствие из закона Гесса используется для определения теплот химических реакций по справочным данным, т.е. по теплотам образования веществ
0 = ![]() ;
; ![]() D
r
H
-?
D
r
H
-?
![]()
![]()
![]()
![]()
![]()
![]() D
r
H
D
r
H
![]()
![]() Реагенты Продукты
Реагенты Продукты
![]()
![]()
![]()
![]()
![]()
![]() Простые вещества
Простые вещества ![]()
Простые вещества одинаковы для реагентов и продуктов, поэтому
![]() D
r
H
=
D
r
H
= ![]()
![]() =
= ![]() (3.1)
(3.1)
Теплота реакции равна сумме теплот образования конечных веществ минус сумма теплот образования исходных веществ с учетом модуля стехиометрических коэффициентов .
4.4.2. Экспериментальное определение теплот реакций .
4.4.2.1. Калориметрия – метод непосредственного экспериментального измерения теплот химических реакций в приборе, называемом калори-метром. Различают калориметры изотермические , работающие при постоянной температуре, и с переменной температурой, которая и служит измеряемой величиной в этом случае. В последнем случае реакцию проводят в адиабатических (по возможности) условиях. В этом случае изменение D U или D H происходят за счет химической реакции и за счет изменения температуры
0 = D r H + D t H = D r H D x + Cp D T
D r H = - Cp D T/ x = - Cp D Tk / D nk (3.2)
4.4.2.2 .Теплота сгорания .
Для экспериментального определения теплоты реакции необходимо, чтобы реакция протекала однозначно, т.е. не сопровождалась побочными процессами и степень превращения приближалась к единице. Далеко не все реакции отвечают таким критериям. Наиболее доступны для экспериментального исследования теплоты сгорания, которые проводят в калориметрической бомбе в атмосфере кислорода без катализатора. При этом получаются устойчивые оксленные состояния элементов СО2 , Н2 О, SO 2 , N 2 или N О2 , обязательно требуется анализ продуктов.
С2 Н5 ОН +7/2 О2 = 2 СО2 + 3 Н2 О; D r Н = D с Н
4.4.2.3. 2-ое следствие из закона Гесса – определение теплоты реакции по теплотам сгорания
![]()
![]() С6
Н6
+ 3Н2
= С6
Н12
D
с
Н1
= -3267,58 кДж/моль
С6
Н6
+ 3Н2
= С6
Н12
D
с
Н1
= -3267,58 кДж/моль
![]() D
с
Н1
D
с
Н 2
D
с
Н3
D
с
Н1
D
с
Н 2
D
с
Н3
| 6 СО2 + 6 Н2 О |
D с Н2 = D f Н(Н2О) = -285,83 кДж/моль
D с Н3 = -3919,91 кДж/моль
| D
r
Н
= |
(3.3)
Теплота реакция равна сумме теплот сгорания реагентов минус сумма теплот сгорания продуктов с учетом модулей стехио-метрических коэффициентов.
4.4.3. 3-ье следствие из закона Гесса – пересчет экспериментальных теплот сгорания на теплоты образования
3 Сграф. + 3 Н2 + 1/2О2 = Н3 С-СО-СН3 D f H -?
![]() -1 C3
H6
O + 4 O2
= 3 CO2
+ 3 H2
O
D
с
Н
= -1785.3 кДж/моль
-1 C3
H6
O + 4 O2
= 3 CO2
+ 3 H2
O
D
с
Н
= -1785.3 кДж/моль
3 Н2 + 1/2О 2 = Н2 О D с Н = -285,8 кДж/моль
3 С + О2 = СО2 D с Н = -393,51 кДж/моль
D
f
H
= ![]() - D
с
Н
(3.4)
- D
с
Н
(3.4)
Теплота образования вешества равна сумме теплот сгорания простых веществ, образующих его, минус теплота сгорания самого вещества
4.5. Приближенный расчет теплот химических реакций по знергиям связи
4.5.1. Энергия связи – это средняя энергия, необходимая для разрыва связи в 1 моле газообразного вещества до состояния газообразных атомов:
HClгаз = H + Сl; D r Н = HCl
H2 Oгаз = 2 Н + О; D r Н = 2 HCl
H2 Oгаз = Н + ОН D r H = 497 кДж/моль
O Н = О + Н D r H = 421 кДж/моль
e ОН = 918/2 = 459 кДж/моль
C учетом других реакций принято считать энергию связи ОН равной e ОН = 467 кДж/моль. Энергию ковалентных химических связей в слож-ных молекулах в первом приближении можно считать величиной адди-тивной, т.е. энергии связи независимы и всегда положительны, так как разрыв связей – реакция эндотермическая. Поэтому энергия обра-зования газообразного вещества из атомов ( D fа H ) может быть приближенно оценена как сумма энергий связи с обратным знаком
D fа H = - D H атомизации = - n р р (3.5)
4.5.2. Расчет стандартной теплоты образования вещества по энергиям связи.
Составим цикл: проведем атомизацию простых веществ, затратив энергию ![]() , образуем из атомов заданное газообразное вещество и переведем его в стандартное состояние, при этом выделится теплота испарения D
v
H
.
, если стандартное состояние жидкое, и теплота плавления D
m
H
, если вещество твердое.
, образуем из атомов заданное газообразное вещество и переведем его в стандартное состояние, при этом выделится теплота испарения D
v
H
.
, если стандартное состояние жидкое, и теплота плавления D
m
H
, если вещество твердое.
3 Сграф. + 3 Н2 + 1/2О2 = Н3 С-СО-СН3 ж ; D f H -?
![]()
![]()
![]() -
D
v
H
-
D
v
H
3 Сгаз. + 6 Н + О = Н3 С-СО-СН3 газ ; D fа H = - n р р .
D
f
H
= ![]() – S
np
e
p
– D
v
H
.
(3.6)
– S
np
e
p
– D
v
H
.
(3.6)
4.6. Цикл Габера-Борна описывает процессы, вносящие вклад в образо-вание ионных кристаллических соединений. Рассмотрим их на примере образования хлорида натрия
Na тв. + Cl 2(газ) = NaCl тв. ; D r Н = D f Ho
Na + газ + С l газ + е -
![]()
![]()
![]()
Есродства Cl = - 354
Na + газ + С l газ
![]()
![]()
![]() Потенциал ионизации
Потенциал ионизации
![]() Na
газ
+ С
l
I = 502
Na
газ
+ С
l
I = 502
![]()
Na газ + С l 2 D H дисс. = 121
![]()
![]() E
рещетки
= 788
E
рещетки
= 788
Na тв. + Cl 2газ D Hc ублим. Na = 108 D H гидр. Na + +
![]()
![]() + D
H
гидр.
Cl
+ D
H
гидр.
Cl
D f Ho = - 411
NaCl тв
 |
Na + aq + С l - aq DHm
![]()
D f Ho = D H субл. Na + D H дисс С l 2 + INa + Есродств a Cl - E рещетки = (3.7)
= 108 + 121 + 502 – 354 – 788 = 411 кДж/моль
4.7. Теплота растворения
Раствор – это фаза переменного состава, существующая в определенных пределах термодинамических параметров. Раствор – гомогенная система, состоящая из двух или более компонентов. Свойства раствора зависят от концентрации, и теплота образования раствора также является функцией концентрации. В процесс растворения вещества вносят вклад процессы разрушения кристаллической решетки (Q 0 ) и процесс сольватации (Q0 ).
4.7.1 Интегральная теплота растворения (D Hm ) – количество теплоты, выделяемое или поглощаемое при растворении 1 моля вещества в таком количестве воды, чтобы была достигнута заданная моляльная концентрация раствора (m)
![]()
![]() D
Hm
D
Hm
 D
H
0
D
H
0
D Hs
![]()
m , моль/1000г растворителя
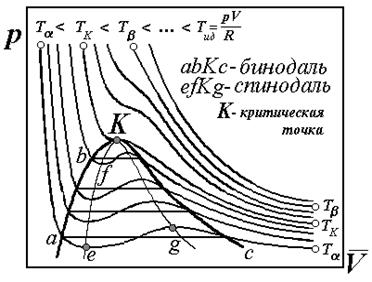
Рис. 4.1. Зависимость теплоты растворения от концентрации раствора
Интегральная теплота растворения изменяется от предельной теплоты в бесконечно разбавленном растворе (D H 0 ) до теплоты растворения в насыщенном растворе (D Hs ) . Величина теплоты растворения ионного крислалла определяется энергией кристаллической решетки и теплотами сольватации катиона и аниона. (см рис. 3.1)
D Hm = E рещетки + D H гидр + + D H гидр - ( 3.8)
4.7.1. Дифференциальная теплота растворения вещества – это количество теплоты, выделяемое или поглощаемое при растворении 1 моля вещества в таком большом количестве раствора заданной концентрации, чтобы при этом концентрация раствора не изменялась.
4.7.3. Теплота разбавления раствора от одной концентрации до другой равна разности между интегральными теплотами растворения
D Hm 12 = D Hm 2 - D Hm 1. ( 3.9)
4.7.4. Теплоты образования ионов в растворе можно представить как суммарную теплоту растворения веществ в растворителе, например, в воде, с образованием гидратированных катионов и анионов. Теплоты образования отдельных ионов можно определить, только если принять теплоту образования какого-либо иона за 0. Условно принимают, что стандартная теплота образования иона водорода равна 0. При этом условии определяются теплоты образования других ионов.
1/2Н2 + 1/2 Cl 2 = HCl газ
HCl + aq = HClaq = Н+ aq + Cl - aq
![]()
1/2Н2 + 1/2 Cl 2 + aq = Н+ aq + Cl - aq , D r H = D f H HCl ( aq ) = D f H H +( aq ) + D f H Cl ( aq ) ; 1/2Н2 + aq = Н+ aq , D f H H +( aq ) =0;
1/2 Cl 2 + aq = Cl - aq , + D f HCl ( aq ) = D r H . ( 3.10)
Лекция № 4
4.8. Зависимость теплоты реакции от температуры
![]() Реагенты Т1
Продукты Т1
; D
r
Hт1
Реагенты Т1
Продукты Т1
; D
r
Hт1
![]()
![]() i
С
р
i
j
С
р
j
i
С
р
i
j
С
р
j
![]() Реагенты Т2
Продукты Т2
; D
r
Hт2
Реагенты Т2
Продукты Т2
; D
r
Hт2
Из изображенного цикла видно, что зависимость теплоты реакции от температуры связана с разностью теплот нагревания реагентов и продуктов реакции, которая связана с их теплоемкостью, которая в свою очередь зависит от температуры.
4.8.1.Зависимость теплоемкости от температуры для идеального газа
4.8.1.1. Связь Ср и С v
С
v
=
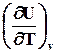 С
p
=
С
p
=
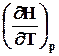
Связь Ср и С v легко определяется для идеального газа:
dH = dU + pdV = dU + p R/p *dT = dU + RdT
(V = RT/p dV = R/p dT)
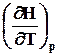 =
=
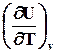 +
R
Cp
=
C
V
+
R
(
4.1)
+
R
Cp
=
C
V
+
R
(
4.1)
R – работа расширения, которую совершает 1 моль идеального газа при нагревании на 1о
4.8.1.2. Энергия молекул как сумма энергий различного вида движения
Внутренняя энергия – это сумма энергии частиц, составляющих термодинамическую систему. В идеальном газе отсутствует энергия взаимодействия молекул, поэтому внутренняя энергия определяется как сумма энергии химических связей в молекулах (e электронная ) и кинетической составляющей движения молекул. Молекулы совершают различные виды движения, и приближенно общую энергию молекул можно представить в виде суммы энергии этих видов движения
e = e электр. + e кол. + e вращ. + e пост. = e е + e v + e r + e t . ( 4.2)
Известно, что энергия микрочастиц квантована, т.е. может принимать только дискретные значения. Расстояние между этими уровнями различно для разных типов движения : D e е D e v D e r D e t (Рис. 4.1).
Поступательная энергия молекул практически не квантуется, т.е. может изменяться непрерывно. Когда системе сообщается тепло, то энергия передается через хаотические соударения молекул. При столкновениях молекулы обмениваются квантами энергии, величина которых зависит от температуры – «тепловыми квантами»– kT , где k – постоянная Больцмана
k = R / N = 1,38*10-23 Дж/К. ( 4.3)
![]()
![]()
![]() e
e
D e е
![]()
![]() kT
kT
![]()
![]()
![]()
![]() D
e
D
e
r
D
e
D
e
r
Рис. 4.1. Квантование уровней различных видов движения
При обычной температуре величина теплового кванта достаточна, чтобы изменить энергию поступательного и вращательного движения, а также наиболее слабых колебаний, но возбуждения сильных колебений, и тем более электронов не происходит
D e v kT D e r ( 4.4)
Эта диаграмма позволяет примерно оценить теплоемкость простейших ве-ществ.
4.8.1.3. Одноатомный газ (He, Ar )
Молекулы одноатомного газа как точечные массы совершают только поступательное движение и имеют три степени свободы. По принципу равномерного распределения энергии по степеням свободы можно определить энергию молекул. На одну степень свободы приходится в среднем e = 1/2 kT , а для 1-го моля Е = 1/2 RT . Cледовательно, на 3 степени свободы одноатомной молекулы приходится
U = 3/2 RT . ( 4.5)
С
v
=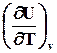 = 3/2
R
~ 3 кал/моль*K = 12,5 Дж/мольК,
= 3/2
R
~ 3 кал/моль*K = 12,5 Дж/мольК,
Cp = C V + R = 5 кал/мольК
Теплоемкость одноатомных газов практически не зависит от температуры.
Таблица 4.1.Теплоемкости С v веществ при разной температуре (кал/мольК)
|
|
nt |
nr |
nv |
150 K |
300 К |
400 К |
| Ar |
3 |
3 |
3 |
2,92 |
2,98 |
2,98 |
| O2 |
3 |
2 |
1 |
4,98 |
5,03 |
6,22 |
| H2 O |
3 |
3 |
3 |
6,04 |
7,57 |
4.8.1.4. Двухатомный газ – линейная молекула
Каждая молекула имеет 3 N степеней свободы, где N –число атомов в молекуле. Для двухатомной молекулы общее число степеней свободы равно 6, из них 3 поступательных, 2 вращательных и 1 колебательная. Вращательных степеней свободы у линейных молекул только 2, так как при вращении вокруг линии связи, молекула не изменяет своего положения и это движение не может изменяться за счет передачи энергии от другой молекулы. При комнатной температуре возбуждаются только поступательное и вращательное движение – 5 степеней свободы
U = 5/2 RT .
С
v
=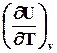 = 5/2 R ~ 5 кал/мольK = 20,8 дЖ/мольК,
= 5/2 R ~ 5 кал/мольK = 20,8 дЖ/мольК,
Cp = C V + R = 7 кал/мольК,
При повышении температуры начинает постепенно возбуждаться колеба-тельное движение, С v 6 кал/(моль К).
4.8.1.5. Многоатомные молекулы . Общее число степеней свободы равно 3 N , из них 3 поступательных, 3 ( или 2 для линейных молекул) враща-тельных и 3 N - 6 (5) колебательных. Колебания тоже могут быть разными: валентные (жесткие) колебания, в которых происходит изменение длины связи, требуют большой энергии для возбуждения, и деформационные , в которых изменяются углы между связями. Последние более мягкие и требуют меньших квантов для возбуждения, и, следовательно, могут возбуждаться при более низкой температуре. В общем можно сделать такой вывод: чем сложнее молекула, тем сильнее зависимость ее теплоемкости от температуры. Нельзя получить общей теоретической формулы, выражающей эту зависимость.
4.8.2. Теплоемкость твердых тел
В твердом теле единственным видом движения является колебания элементов кристаллической решетки, ячейки которой повторяются в пространстве. Твердое тело (например, металл) можно представить как набор гармонических осцилляторов, колеблющихся с одинаковой частотой n . Исследуя такую модель, Эйнштейн вывел теоретическую формулу для расчета теплоемкости твердого тела на основании статистической термодинамики
С v = 3 R ( q / T )2 e q / T , где ( 4.6)
![]() (e
q
/T
–1)2
(e
q
/T
–1)2
где q = h n / k называется характеристической температурой.
При низкой температуре q/T µ, a теплоемкость 0
При высокой температуре q/T 0, a теплоемкость 3 R
Закон Дюлонга и Пти для простых веществ:
С v = суд. М = 6,3 кал/моль.К, где М - атомная масса элемента ( 4.7)
При очень низких температурах вблизи абс. нуля справедлив закон Дебая:
С v = а Т3 ( 4.8)
4.8.3. Представление температурной зависимости теплоемкости в виде температурного ряда. Так как теоретических общих уравнений для зависимости теплоемкости от температуры нельзя вывести, то используются экспериментальные зависимости в виде степенного ряда
для органических веществ Ср = а + bТ + сТ2 + dT 3 ; ( 4.9)
для неорганических веществ Ср = а + bТ + с Т-2 . ( 4.10)
4.8.4. Уравнение Кирхгоффа – зависимость теплоты реакции от температуры
Используя уравнения связи теплот химических реакций с изменением термодинамических функций легко вывести зависимость их от температуры
QV
=
D
r
U =
![]() , (
2.14, 2.15)
, (
2.14, 2.15)
Qp
=
D
r
H =
![]() . (
2.16)
. (
2.16)
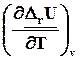 =
= 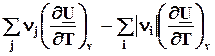 =
= 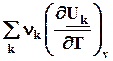 =
= ![]() = D
r
С
v
, (
4.11)
= D
r
С
v
, (
4.11)
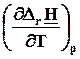 =
= 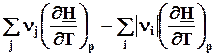 =
= 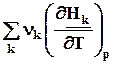 =
= ![]() = D
r
С
p
. (
4.12)
= D
r
С
p
. (
4.12)
D r С p . = D а + D bT + D cT2 + D d T3 + D cT-2 . ( 4.13)
4.8.5. Анализ уравнения Кирхгоффа
4.8.5.1. D r Ср = 0 D r Н T 1 = D r Н T 2 . Теплота реакции не зависит от температуры.
4.8.5.2. D Ср 0, T D r Н Для эндотермической реакции D r Н2 D r Н1 .
Для экзотермической реакции D r Н2 D r Н1 .
4.8.5.3. D Ср 0, T D r Н Для эндотермической реакции D r Н2 D r Н1 .
Для экзотермической реакции D r Н2 D r Н1 .
![]() Ср
реагенты D
r
Н
D
r
Ср
= 0
Ср
реагенты D
r
Н
D
r
Ср
= 0
![]()
![]()
 продукты
продукты
D r Ср 0 D r Ср 0
![]()
![]()
a) T б) Т
Рис. 4.3. Зависимость теплоемкости (а) и теплоты реакции (б) от температуры
4.8.6. Интегрирование уравнения Кирхгоффа
4.8.6.1. Для пересчета теплоты реакции с одной температуры на другую нужно использовать определенный интеграл
 (
4.14)
(
4.14)
D
НТ
=
D
Н298
+ 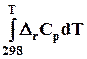 =
D
Н298
+
D
r
Ср
(T-298)
=
D
Н298
+
D
r
Ср
(T-298)
В небольшом интервале температур D r Ср = const . В противном случае нужно представить D r Ср в виде температурного ряда и только после этого интегрировать уравнение ( 4.17)
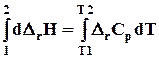 =
= 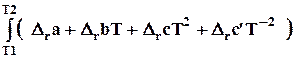 dT
dT
D r Н2 = D r Н1 + D r a ( T 2 - T 1 ) + D r b /2 ( T 2 2 – T 1 2 ) + D r c /3( T 2 3 - T 1 3 ) - D r c (1/ T 2 –1/ T 1 ).
( 4.15)
4.8.6.2. Для вывода общего уравнения зависимости D Н = f ( T ), нужно брать неопределенный интеграл
D r Н = D r Н 0 + D r aT + D r b/2 T2 + D r c/3 T3 - D r c1/T. ( 4.16)
Постоянная интегрирования D r Н0 имеет смысл теплоты реакции при температуре 0 К и может быть найдена по известному значению теплоты реакции при определенной температуре, например, при 298 К
D r Н0 = D Н298 –( D r a 298 + D r b/2 2982 + D r c/3 2983 - D r c1/298). ( 4.17)
Температурные ряды теплоемкостей могут быть оборваны на любом члене в зависимости от выбранного интервала температур: чем больше разность температур, темболшее число членов температурных полиномов следует учитывать.
Лекция № 5
5. Второй закон термодинамики
Первый закон термодинамики устанавливает эквивалентность различных видов энергии и форм их передачи. 2-ой закон термодинамики говорит скорее об обратном. Теплота и работа в определенном смысле неэквивалентны – всю работу можно превратить в тепло, а все тепло перевести в работу в периодическом, т.е. циклически повторяющемся процессе нельзя. Все самопроизвольные процессы протекают в одном направлении. Назначение 2-го закона термодинамики – установление критериев самопроизвольного протекания разнообразных процессов.
5.1. Классификация процессов с точки зрения 2 закона термодинамики.
5.1.1. Самопроизвольные процессы выравнивания, протекающие в системе без внешних воздействий, они идут до установления равновесия. Самопроизвольные процессы всегда протекают в одном направлении.
За счет самопроизвольных процессов может быть получена работа: например, за счет разности давлений можно получить механическую работу или работу электрическую - пьезоэлектричество; за счет разности температур может работать тепловой двигатель или термопара, в процессе установления химического равновесия можно получить электрическую работу – в гальваническом элементе.
5.1.2. Несамопроизвольные не могут протекать в системе в отсутствие внешних сил
5.1.3. Обратимые, равновесные, квазистатические, или регулируемые процессы, после циклического их завершения не остается никаких изменений ни в системе, ни в окружающей среде. Это идеализированные процессы, которые характеризуются следующими особенностями:
1) внешние и внутренние силы почти скомпенсированы и различаются на бесконечно малую величину, например ре » -р i ;
2) могут изменять направление при бесконечно малом изменении внешних сил;
3) в прямом и обратном направлении процесс протекает через одни и те же промежуточные состояния – по одному и тому же пути;
4) бесконечно медленно;
5) могут быть изотермическими или адиабатическими;
6) | d W | полученная = | d W | затраченная ;
7) d W обр = d Wmax . d W необр ..
8) Необратимых путей множество, а обратимый только один. Для проведения обратимого процесса нужно искусственно тормозить его, прилагая внешнюю силу, преодоление которой позволяет извлекать из системы максимальную работу. Для получения такого результата необходимо иметь некоторое усторойство (тепловой двигатель, галь-ванический элемент и т.п.). Обратимый – идеализированный полностью регулируемый процесс.
5.2. Формулировки второго закона термодинамики. Закон прошел длительный путь эволюции и сначала был сформулирован как основной закон действия тепловых машин
5.2.1. Теорема Карно (1824) “Размышление о движущей силе огня” – коэффициент полезного действия обратимого цикла, состоящего из 2 изотерм и 2 адиабат, зависит только от разности температур тепловых резервуаров и не зависит от природы рабочего тела
h = (Q1 – Q2 )/Q1 = (T1 –T2 )/T1 = 1 – Т2 /Т1 . ( 5.1)
5.2.2. Томсон (лорд Кельвин) (1848) ввел понятие абсолютной температуры и (1851) сформулировал 2 закон ТД – невозможно построить периодически действующую тепловую машину, которая только бы черпала тепло из одного резервуара и производила механическую работу, т.е. невозможен вечный двигатель 2-го рода
5.2.3. Клаузиус (1850) дал первую формулировку 2 закона ТД – невозможен самопроизвольный переход теплоты от тела менее нагретого к телу более нагретому . Обе формулировки эквивалентны, одна невозможна без другой. (1854) Ввел понятие энтропии .
5.2.4. Математическое выражение 2 –го закона ТД
Для каждой фазы a , содержащей k компонентов, существует аддитивная функция состояния, называемая энтропией
S
a
= S
a
(U
a
, V
a
, n1
a
, n
a
2
, ..n
a
k
);
![]() , S =
, S = ![]() , D
S = S2
– S1
, D
S = S2
– S1
![]() изменение которой следующим образом связано с теплотой и температурой процесса
р
изменение которой следующим образом связано с теплотой и температурой процесса
р
 dS
=
dS
=
![]()
![]() для обратимых процессов; (5.1) p1
V1
T1
S1
для обратимых процессов; (5.1) p1
V1
T1
S1
![]() dS
dS
![]() для необратимых процессов. (5.2) p2
V2
T2
S2
для необратимых процессов. (5.2) p2
V2
T2
S2
(Неравенство Клаузиуса) V
Рис. 5.1. К понятию энтропии.
Температура – интегрирующий делитель, который превратил функцию процесса в изменение функции состояния, а энтропия – тепловая координата.
Работу всегда можно выразить как произведение интенсивного параметра на изменение экстенсивного
d
W
= -
![]() , (
5.3),
, (
5.3),
а теплоту – аналогично d Q = TdS – для обратимых процессов, (5.4)
где Т – интенсивный параметр, а dS изменение экстенсивного свойства.
Объединяя 1 и 2 законы термодинамики (уравнения 2.2 и 5.1), получаем
d U = TdS – pdV
+ ![]() . (5.5)
. (5.5)
5.2.5. Анализ уравнений типа (5.5) привел Каратеодори к новой формулировке 2-го закона термодинамики, не связанной с тепловыми машинами:
вблизи любого состояния термически однородной и адиабатически изолированной системы есть бесконечное множество других состояний, не достижимых адиабатическим путем . В этом случае Т становится интегрирующим делителем, а S – функцией состояния.
5.3 Расчет изменения энтропии в различных процессах .
Изменение энтропии нельзя непосредственно измерить, измерять можно только теплоту. Количество теплоты может быть различным в обратимом и необратимом процессе, но изменение энтропии в них должно быть одинаковым, если одинаковы начальное и конечное состояния
dSобр.
= ![]() обр.
обр.![]()
![]()
![]()
S2
– S1
= dSнеобр.
![]() необр
необр ![]() обр.
обр.![]()
![]() необр. (5.6)
необр. (5.6)
Как и работа, теплота обратимого процесса всегда больше теплоты необ-ратимого при заданных начальном и конечном состояниях.
5.3.1. Изменение температуры в закрытой сиситеме
5.3.1.1. V
=
const
.
dS
= ![]()
![]() =
= 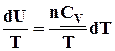
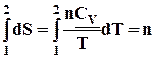
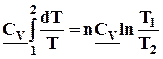 , (5.7)
, (5.7)
если СV = const, т.е. интервал температур небольшой, в противном случае нужно в подинтегральную функцию ввести теплоемкость в виде темпе-ратурного ряда.
5.3.1.2. p
=
const
. 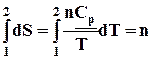
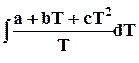
D
S
= n[ ]. (5.8)
]. (5.8)
D SV = 5 кал/(моль*К)* ln 373 K /273 = 1,56 кал/(моль*К) = 6,53Дж/(моль*К)
С и S имеют одинаковую размерность.
5.3.2. Изотермическое расширение-сжатие идеального газа
dS
= ![]() ; DS
=
; DS
=
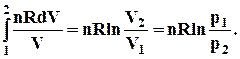 (5.9)
(5.9)
5.3.3. Смешение газов. Модель смешения при постоянных давлении и температуре может быть предствалена так:
 |
 |
na , Va nb Vb na , nb, Va + Vb
p,T p,T p,T
![]()
![]()
nk / S nk = Nk мольная доля
D
S =
D
Sa
+
D
S
b
= na
R ln
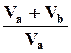 + nb
R ln
+ nb
R ln
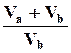 =
=
= na
R ln 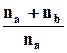 + nb
R ln
+ nb
R ln 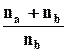 = -R(na
ln Na
+ nb
lnNb
).
(5.10)
= -R(na
ln Na
+ nb
lnNb
).
(5.10)
Изменение энтропии при смешении газов зависит от концентрации получаемой смеси, Это изменение всегда положительно, так как мольная доля всегда меньше единицы, а ее логарифм – отрицателен.
5.3.4. Фазовые переходы
dS
= 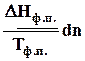 D
S
=
D
S
= 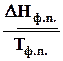 ,
(5.11)
,
(5.11)
так как фазовые переходы чистых веществ произходят при постоянной температуре, если зафиксировано давление.
5.3.5. Химические реакции
D r S = S n j Sj - S n i Si = S n k Sk . (5.12)
5.4. Энтропия – критерий направления самопроизвольных процессов в изолированной системе. d Q = 0, dV = 0, d U = 0
dSU,V 0 самопроизвольный процесс; (5.13)
dSU,V = 0 равновесие; (5.14)
в стабильном равновесии изолированная система достигает максимума энтропии (dS 2 / d Х2 ) U , V 0. (5.15)
В неизолированной системе энтропия может уменьшаться, но при этом должен происходить рост энтропии в окружающей среде.
Таблица 5.1. Изменение энтропии в различных процессах в системе и окружающей среде
| Процесс |
DSсистемы |
DSокр. среды |
DSобщ. |
| Циклический обратимый |
0 |
0 |
0 |
| Нециклический обратимый |
0 |
0 |
0 |
| - “ - |
0 |
0 |
0 |
| Циклический необратимый |
0 |
0 |
0 |
| Нециклич. необратимый |
0 |
0 |
0 |
| - “- |
0 |
0 |
0 |
Лекция № 6
5.5. Статистический смысл энтропии
Термодинамические соотношения не зависят от природы веществ, но термодинамические свойства индивидуальных соединений находят опытным путем. Задача статистической термодинамики – определение характеристик веществ на основании свойств образующих их частиц, законов их движения и взаимодействия. Статистическая термодинамика начала развиваться с конца XIX века. Основные принципы ее были разработаны в трудах Больцмана, Гиббса, Планка, Эйнштейна, Эренфеста, Т. Афанасьевой-Эренфест.
5.5.1. Макро- и микросостояния термодинамической системы . Макро- состояние системы задается набором термодинамических параметров, которые имеют смысл для всей системы в целом.
Микросостояние – это состояние отдельных частиц системы, которые можно разделить на квантовые и классические. Критерием отнесения может служить соотношение разности энергетических уровней D e и энергией теплового кванта kT : если D e kT , то соответствующая степень свободы относится к квантовым характеристикам, в противном случае – к классическим. Будем полагать, что квантовые характеристики постоянны и классическое движение ограничивается поступательным. Тогда для задания состояния каждой частицы необходимо задать для каждой частицы 3 координаты – х k , yk , zk и 3 проекции импульса рх k , ру k и р zk , т.е. всего 6 N переменных, где k $ 1,2, 3… N . Для термодинамических систем
N очень велико, и это приводит к новым, статистическим закономерностям, которые нельзя свести к механическим. Характерной чертой их является представление о динамических переменных как случайных величинах, которым можно приписать определенную вероятность.
5.5.2. Фазовое пространство . Наглядно состояние системы можно представить, используя понятие фазового пространства. Фазовое пространство – математическое понятие, это условное пространство возможных микросостояний системы. Когда Вы изображали электронные конфигурации атомов в виде клеточек, заполненных электронами, то имели дело с фазовым пространством электронов в атоме. В нашем случае координатами фазового пространства служат координаты и проекции импульсов частиц, т.е. это пространство 6 N -мерное, микросостояние всей системы изображается точкой в этом пространстве, при изменении состояния изображающая точка описывает траекторию в фазовом пространстве. Такое пространство обозначают как Г-пространство .
Но молекулы одного вещества обладают одинаковыми свойствами, поэтому можно свести описание микросостояния системы к рассмотрению 6-мерного m - пространства, в котором распределяются N точек - частиц.
Таблица 6.1. Размерности фазовых пространств одноатомного газа
| Фазовое пространство |
Размерность |
Описание микро-состояния системы |
Изменение состояния |
| Г |
6N |
Точка |
Линия |
| m |
6 |
Распределение N точек |
Изменение распределения |
Изменение координат и импульсов происходит непрерывно, поэтому кажется, что состояний бесконечное множество, и сосчитать их очень трудно. Так было во времена Гиббса, в последней четверти ХIХ в. Однако развитие квантовой теории сделало фазовое пространство счетным, когда Гейзенбергом был сформулирован принцип неопределенности, который позволяет разбить фазовое пространство на счетное количество фазовых ячеек, каждая из которых отвечает различимому микросостоянию частицы:
D х * D рх h для одномерного движения (6.1)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() D
х
*
D
рх
*
D
у
*
D
ру
*
D
z
*
D
рz
h
3
для движения в трехмерном пространстве.
D
х
*
D
рх
*
D
у
*
D
ру
*
D
z
*
D
рz
h
3
для движения в трехмерном пространстве.
рх Каждая ячейка отвечает определенному отличимо-
![]()
![]() му состоянию частицы.
му состоянию частицы.
х
Рис 6.1. Ячейки фазового пространства одномерного движения
5.5.3. Термодинамическая вероятность.
5.5.3.1. В равновесии термодинамические параметры системы постоянны , но микрохарактеристики молекул претерпевают непрерывные изменения. Таким образом, макросостояния системы реализуется множеством микросостояний. Число микросостояний, совместимых с данным макросостоянием, называется термодинамической вероятностью
5.5.3.2. Принципы расчета термодинамической вероятности.
5.5.3.2.1. Микросостояния отличаются друг от друга перестановкой частиц.
5.5.3.2.2. Перестановки внутри одной ячейки не ведут к новому микросостоянию, так как состояния внутри ячейки неразличимы.
5.5.3.2.3. В одно макросостояние входят все микросостояния с одинаковым количественным распределением частиц по ячейкам, т.е. задать макросостояние на микроуровне можно определением числа частиц в каждой ячейке фазового пространства Ni .
5.5.3.2.4. Основной постулат – для изолированной системы (U = const ): все S N
микросостояний имеют одинаковую вероятность, т.е. функция распределения r = const. Это позволяет легко рассчитывать термодинамическую вероятность состояния системы, состоящей из N частиц, распределенных по s ячейкам фазового пространства, используя формулу комбинаторики для числа перестановок:
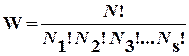 , (6.2)
, (6.2)
Пример: 2 частицы в двух ячейках (микросостояниях), N = 2, S = 2.
| 1, 2 |
2 |
1 |
| 1 |
2 |
1, 2 |
4 микросостояния (22 ) разбиты на 3 макросостояния:
| N1 |
N2 |
W |
| 1 |
1 |
2 |
| 0 |
2 |
1 |
| 2 |
0 |
1 |
5.5.3.3. Наибольшая термодинамическая вероятность получается при равномерном распределении N частиц по ячейкам с одинаковой энергией.
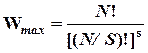 . (6.3)
. (6.3)
С увеличением числа частиц термодинамическая вероятность равномерного распределения частиц по ячейкам очень сильно возрастает
N S Wmax
2 2 2
4 2 6
6 3 15
15 3 756756
5.5.3.4. Направление самопроизвольных процессов. Изолированная термодинамическая система стремится к состоянию с наибольшей термодинамической вероятностью, которое достигается при установлении равновесия.
5.5.4. Связь энтропии с термодинамической вероятностью предложена на основании свойств энтропии и термодинамической вероятности
Аддитивность энтропии S = f(W); S = S1 + S2 .
Мультипликативность термодинамической вероятности W = W 1 * W 2 .
S(W) = S(W1 *W2 ) = S1 (W1 ) + S2 (W2 ) S = k ln W, (6.4)
где k – постоянная Больцмана.
Таким образом, энтропия характеризует неупорядоченность системы, ее беспорядок.
5.5.5. Процессы , ведущие к увеличению энтропии
5.5.5.1. Увеличение числа частиц, например, распад молекул, диссоциация.
5.5.5.2. Увеличение объема фазового пространства, т.е. увеличение числа ячеек, или возможных состояний.
а) увеличение объема, расширение; смешение, свертывание полимера в клубок;
б) увеличение числа доступных уровней энергии, густота энергетического спектра, уменьшение расстояния между уровнями. Это связано с характером движения. Наиболее беспорядочно поступательное движение, затем следует вращательное, колебательное.
5.5.6. Распределение молекул по энергии при постоянной темп ературе.
Система и термостат образуют изолированную систему, но сама система мала по сравнению с термостатом. В этих условиях частицы будут обладать разной энергией e i в состоянии равновесия, Ni – число частиц на i -уровне.
N1 e 1 S Ni = N = const; S e i Ni = U = const
N 2 e 2
Nm ……………e m ……
Распределение Больцмана: ![]() (6.5)
(6.5)
где gi
–кратность вырождения уровня, т.е. число состояний с заданным i- уровнем энергии 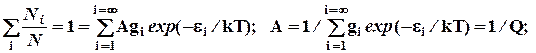 (6.6)
(6.6)
![]() где Q
– статистическая сумма
, характеристика, которая связывает свойства частиц (набор их допустимых энергетических уровней и кратность их вырождения) с макроскопическим параметром – температурой. Поэтому именно эта величина будет фигурировать далее во всех формулах статистической термодинамики.
где Q
– статистическая сумма
, характеристика, которая связывает свойства частиц (набор их допустимых энергетических уровней и кратность их вырождения) с макроскопическим параметром – температурой. Поэтому именно эта величина будет фигурировать далее во всех формулах статистической термодинамики.
![]() Q
=
Q
=
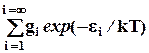 ;
(6.6)
;
(6.6)
![]() (6.7)
(6.7)
6. Третий закон термодинамики
6.1. Формулировки
6.1.1. Тепловая теорема Нернста (1906 г.)
При температуре, близкой к абсолютному нулю, многие свойства системы становятся независимыми от температуры, т.е. становятся постоянными, например теплоты химических реакций, объем системы, поверхностное натяжение и др.
![]() . (6.8)
. (6.8)
Теплоемкости всех веществ становятся одинаковыми и стремятся к 0. Изменение энтропии при всех процессах при абсолютном нуле равно 0.
6.1.2. Постулат Планка: энтропия идеального кристаллического тела при абсолютном нуле равна 0 . Статистическое обоснование постулата Планка – все частицы находятся на низшем энергетическом уровне, т.е. занимают 1 ячейку фазового пространства. Термодинамическая вероятность такого состояния равна 1, а энтропия = 0.
6.1.3. Недостижимость абсолютного нуля . Охлаждение достигается за счет
адиабатического расширения (DТ 0) и изотермического сжатия (DS 0), при последнем процессе нужно отводить тепло, что возможно только к менее нагретому телу. При абсолютном нуле невозможно понизить энтропию, поэтому абсолютный нуль недостижим, хотя в настоящее время достигнуты температуры в несколько тысячных градуса Кельвина.
6.2. Остаточная энтропия
Реальные кристаллы могут иметь дефекты – дырки по Шоттки и Френкелю, дислокации, нарушения кристаллической решетки, основной уровень может быть вырожденным. В этих случаях энтропия при абсолютном нуле будет иметь значение, отличное от 0, которое называется остаточной энтропией. Ее можно оценить статистическим методом по формуле S = R ln g 0 , (6.9)
где g 0 – кратность вырождения низшего уровня.
Аналогично можно рассчитать остаточную конфигурационную энтропию, возникающую, если существует несколько энергетически равноценных ориентаций молекулы в кристаллической ячейки, например, при изотопном замещении. Рассмотрим молекулу метана, в которой 1 атом водорода замещен на дейтерий. Атом дейтерия может занимать одно из 4 положний в ориентированной молекуле метана. Каждое из этих положений можно рассматривать как возможное состояние в фазовом пространстве кристалла (g =4) , эти состояния равновероятны. Следовательно, наиболее вероятным будет равномерное распределение, и термодинамическая вероятность будет рассчитаывться по формуле (6.5). Для очень большого числс частиц (1 моль =6,02 1023 ) с использованием формулы Стирлинга для расчета N!, остаточная конфигурационная энтропия может быть определена по формуле S = R ln g .
6.3. Абсолютная энтропия – это изменение энтропии, отсчитанное от абсолютного нуля до данного состояния. Для ее расчета необходимо суммировать изменение энтропии во всех процессах нагревания и фазовых переходах:
![]()
![]()
![]() 0 К Нагревание твердого тела Нагревание жидкости Нагревание газа
0 К Нагревание твердого тела Нагревание жидкости Нагревание газа
Плавление Кипение.
Небольшой участок температурной шкалы вблизи абсолютного нуля (до 10-15К) недоступен для экспериментального измерения теплоемкости, изменение энтропии на нем можно рассчитать, используя уравнение Дебая
(4.8). В таком случае мольная абсолютная энтропия вещества рассчитывается по уравнению
S
=
C
p
(15)
/3 +
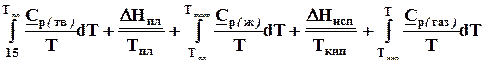
(6.10).
Уравнение (6.10) может быть оборвано на любом слагаемом, если вещества представляют собой твердые или жидкости в стандартном состоянии. Если газ не идеальный, то для стандартного значения энтропии нужно внести поправку.
Лекция № 7
7. Применение 2-го закона термодинамики к изотермическим процессам
7.1. Фундаментальное уравнение Гиббса
Уравнение 2-го закона не очень удобно для использования, так как в нем характеристики системы выражаются через функции процесса. Желательно, чтобы свойства системы выражались через ее параметры. Для этого можно объединить уравнения 1-го (2.2) и 2-го (5.1) законов термодинамики
dS =1/Т dU + p /Т dV + d W ’ , (7.1)
для закрытой системы dW’=0
dS = 1/ T dU + p / T dV (7.2)
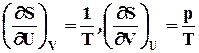 ; S
=
f
(
U
,
V
)
. (7.3)
; S
=
f
(
U
,
V
)
. (7.3)
Энтропия системы является функцией от внутренней энергии и объема, производные по этим параметрам выражаются через отношение интенсивных характеристик системы, направление самопроизвольных процессов в закрытых системах выражается неравенством dSU , V 0 . Уравнение (7.2) называется фундаментальным уравнением Гиббса для закрытых систем в энтропийном выражении.
Перепишем это уравнение для внутренней энергии:
dU = TdS – pdV (7.4)
Последнее содержит эквивалентную информацию о системе и также назы-вается фундаментальным уравнением Гиббса для закрытых систем в энергетическом выражении. Отсюда следует, что
U
=
f
(
S
,
V
);
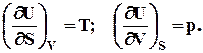 (7.5)
(7.5)
Преимущество уравнения (7.4) состоит в том, что интенсивные характери-стики системы (р,Т) выражаются непосредственно как частные производные внутренней энергии по параметрам.
Из сравнения (2.2) (5.2) следует
dU TdS - pdV - d W ’. (7.6)
Направление самопроизвольных процессов при постоянстве энтропии и объема может быть выражено через изменение внутренней энергии:
dUS , V 0.
Такая ситуация имеет место в механических системах, в которых энтропия постоянна. Устойчивое равновесие достигается при минимуме внутренней энергии:
dUS , V = 0; ( d 2 U / d Х2 ) S , V 0. (7.7)
7.2. Критерии направления самопроизвольных процессах в изотермических условиях. Термодинамические потенциалы.
Фундаментальные уравнения Гиббса определяют свойства термодинамических систем, когда в качестве независимых переменныых выступают экстенсивные параметры (U , V или S , V ), которые нельзя непосредственно контролировать. Это делает их неудобными для их практического использования. В связи с этим требуется преобразовать эти уравнения таким образом, чтобы независимыми параметрами стали бы контролируемые величины, удобнее всего интенсивные (именно в этих условиях обычно проводятся химические реакции) при сохранении характеристичности функций.
7.2.1. Энергия Гельмгольца.
7.2.1.1. Физический смысл
Преобразуем выражение (7.6) таким образом, чтобы функции состояния попали в одну сторону неравенства – влево:
dU - TdS - d W .
Представим изотермический процесс и проинтегрируем это уравнение
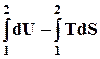 -WT
D
U - T
D
S
-WT
U2
– U1
– T(S2
– S1
)
-WT
.
-WT
D
U - T
D
S
-WT
U2
– U1
– T(S2
– S1
)
-WT
.
( U 2 – TS 2 ) – ( U 1 – TS 1 ) = D A - WT . (7.8)
Получили новую функцию состояния, называемую энергией Гальмгольца
A U – TS (7.9)
![]() ; D
A = A2
– A1
.
; D
A = A2
– A1
.
D A -WT ; - D A WT ; - D A= (WT )max (7.10)
Убыль энергии Гельмгольца равна максимальной работе обратимого изотермического процесса. В необратимом процессе работа полученная оказывается меньше убыли энергии Гельмгольца, а затраченная забота больше роста энергии Гельмгольца.
7.2.1.2. Направление самопроизвольных процессов при Т, V = const .
Напишем полный дифференциал энергии Гельмгольца и подставим в него фундаментальное уравнение Гиббса (7.6)
dA = dU – TdS – SdT dA TdS - pdV - d W’ – TdS – SdT
dA - SdT - pdV - d W ’ .
При Т,V = const в самопроизвольном процессе dW’0, отсюда критерием на-
правления самопроизвольного процесса будет уменьшение энергии Гельмгольца
dA V,T 0 при Т ,V = const (7.11)
Стабильное равновесие достигается при минимуме энергии Гельмгольца.
dA V,T = 0; (d2 A/d Х 2 ) V,T 0 (7.12)
– условие стабильного равновесия при Т, V = const.
7.2.1.3. Полный дифференциал энергии Гельмгольца в зaкрытой системе
dA = – SdT – pdV (7.13)
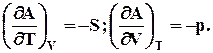 (7.14)
(7.14)
С ростом температуры и объема энергия Гельмгольца всегда падает, так как энтропия и давление системы всегда имеют положительное значение, и производные будут отрицательными.
7.2.2. Энергия Гиббса .
7.2.2.1. Физический смысл
Проинтегрируем фундаментальное уравнение Гиббса при T, p = const
dU - TdS + pdV - d W ’
d ( U – TS + PV ) - d W ’
D ( U – TS + PV ) - W ’ p , T
Новая функция состояния – энергия Гиббса
G U + pV – TS ; (7.15)
![]() ,
D
G
=
G
2
–
G
1
.
,
D
G
=
G
2
–
G
1
.
D G - W ’ p , T ; - D G W ’ p , T ; - D G = W ’ p , T ( max ) (7.16)
Убыль энергии Гиббса равн a максимальной полезной работе изобарно-изотермического процесса.
7.2.2.2. Критерии направления самопроизвольного процесса при T , p = const .
dG p , T 0, D G p , T 0. (7.17)
Процессы при T,p = const идут в сторону убыли энергии Гиббса.
Стабильное равновесие достигается при минимуме энергии Гиббса
dG p,T = 0 ; (d 2 G/d Х 2 ) p,T 0. (7.18)
7.2.2.3. Полный дифференциал энергии Гиббса в закрытой системе
dG = dU + pdV + Vdp – TdS – SdT из определения функции.
Подставим фундаментальное уравнение Гиббса (7.4)
dG = TdS - pdV + pdV + Vdp – TdS – SdT = Vdp – SdT .
Определяющими параметрами для энергии Гиббса будут – р и Т,
dG = Vdp – SdT (7.19)
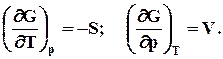 (7.20)
(7.20)
7.3. Характеристические функции
7.3.1. Определение. Характеристические функции - это экстенсивные функции состояния системы, посредством которых, а также производных от них различных порядков по соответствующим параметрам, выражаются все свойства системы . Удобством характеристических функций, полученных преобразованием фундаментального уравнения Гиббса в энергетическом выражении (7.4), служит то, что интенсивные параметры системы получаются непосредственно через частные производные этой функции. Эти функции называют термодинамическими потенциалами, хотя характеристично-стью обладает энтропия и другие функции, получающиеся преобразованием уравнения (7.1) . Каждая характеристическая функция состояния связана со своим набором переменных. Мнемоническое правило P V
![]()
![]()

 S T
S T
U H A G
Можно написать внутреннюю энергию как функцию T , V: U = f ( T,V). Полный дифференциал ее определяется в таком случае так:
dU
= 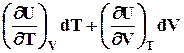
CV 0 (Для идеальных газов)
Таким образом, при указанных независимых переменных внутренняя энергия не является характеристической функцией, так как в этом случае не определены энтропия и давление - важнейшие характеристики системы.
7.3.2. Таблица характеристических функций ( F )
| F |
Естествен- ные параметры |
Условия самопро- извольных процессов |
Условия равновесия |
Производные функций |
Физиче-ский смысл |
| U |
S,V |
D US,V 0 |
D US,V =0
|
|
D U= QV |
| H |
S, р |
D HS,p 0 |
D HS,p =0 d2 H0 |
|
D H = Qp |
| A |
T,V |
D AT,V 0 |
D AT,V =0 d2 A0 |
|
- D A = (WT )max |
| G |
T,p |
D G p,T 0 |
D G p,T =0 d2 G0 |
|
- D G = (W’pT )max |
7.3.3. Полные дифференциалы и частные производные характеристиче-ских функций в закрытых системах (урпанения Массье)
dU = TdS – pdV Эти выражения получились как преобразования
d Н = TdS – Vdp фундаментального уравнения Гиббса к другим
dA = – SdT – pdV переменным, но содержат эквивалентную ему
dG = Vdp – SdT информацию.
В этих выражениях термодинамические параметры получили свое определение, независимое от эмпирической основы. Производные от характеристических функций по экстенсивным параметрам дают интенсивные характеристики системы и, наоборот, производные по интенсивным переменным приводят к экстенсивным параметрам. В фундаментальном уравнении Гиббса естественными параметрами служат экстенсивные величины - энтропия и объем. Это очень неудобно для практических целей, так как нет способа поддерживать постоянную энтропию в ТДС. В то же время интенсивные параметры легко контролировать в различных процессах, поскольку они выравниваются автоматически в состоянии равновесия. Поэтому наиболее важной функцией для химиков является энергия Гиббса, для которой определяющими параметрами служат температура и давление. При постоянстве этих параметров проходит большинство химических процессов. Поэтому остановимся более подробно на анализе этой функции.
7.3.4. Зависимость энергии Гиббса от температуры и давления
G U + pV– TS H – TS (7.21)
D G pT D H -T D S, D r G pT D r H -T D r S (7.22)
D H характеризует общее изменение энергии системы в ходе процесса, а изменение энергии Гиббса показывает, какая часть ее может быть превращена в полезную работу, поэтому раньше ее называли свободной энергией, в противоположность энтропийному члену, который характеризовал связанную энергию, недоступную для превращения в работу.
а) ; б)
; б) 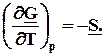 (7.20)
(7.20)
Из уравнения 7.20а следует, что с ростом давления энергия Гиббса увеличивается, так как V 0 , но темп роста замедляется, так как объем постепенно уменьшается. Причем для разных идеальных газов эти кривые будут одинаковыми.
![]()

![]() G
T = const G
p = const
G
T = const G
p = const
 |
p T
Рис. 7.1. Зависимость энергии Гиббса от давления и температуры.
С ростом температуры энергия Гиббса убывает, так как энтропия всегда положительна, причем падение энергии Гиббса будет ускоряться из-за роста энтропии при повышении температуры.
7.3.5. Уравнение Гиббса – Гельмгольца. Эта зависимость позволяет заменить недоступную для непосредственных измерений функцию – энтропию на измеряемую величину - температурную зависимость энергии Гиббса. В результате подстановки этого выражения в уравнение (7.21) получаем
G
H
+
T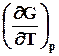 (7.23)
(7.23)
Аналогично можно представить энергию Гельмгольца
А
U
+
T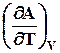 (7.24)
(7.24)
Уравнения (7.24) и (7.25) называется уравнениями Гиббса-Гельмгольца . Можно произвести с ними дальнейшие преобразования: из уравнения (7.24) следует
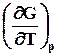 =
= ![]() . (7.25)
. (7.25)
Далее рассмотрим производную от дроби G / T и подставим в нее выраже-ние (7.26):
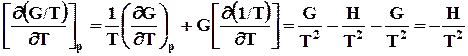 . (7.26)
. (7.26)
Таким образом зависимость приведенной энергии Гиббса G / T от температуры определяется энтальпией системы. Уравнение (7.27) также называют урав-нением Гиббса –Гельмгольца. Аналогично для энергии Гельмгольца можно написать
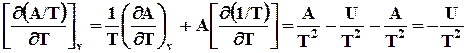 . (7.27)
. (7.27)
Уравнения Гиббса-Гельмгольца находят применение для физических и химических процессов. Для этого требуется заменить в них термодина-мические потенциалы на их изменение в указанных процессах, например
r
G
=
r
H
+
T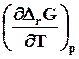 ,
или (7.28)
,
или (7.28)
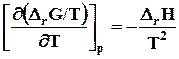 и (7.29)
и (7.29)
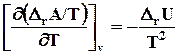 . (7.30)
. (7.30)
Лекция № 8
8. Фундаментальное уравнение Гиббса для открытых систем
8.1 . Дифференциалы характеристических функций
dU = TdS – pdV - d W ’
Гиббс ввел в качестве переменной массу, а точнее количество молей компонентов, т.е. для открытых систем нужно учесть химическую работу, которую можно представить как обмен веществом с окружающей средой.
d
W
хим
.
= - ![]() .
.
dU = TdS – pdV +
![]() . U = f ( S, V, nk
)
(8.1)
. U = f ( S, V, nk
)
(8.1)
dН = TdS + Vdp
+ ![]() . H = f ( S, p, nk
)
(8.2)
. H = f ( S, p, nk
)
(8.2)
dA = - SdT – pdV +
![]() . A = f (V, T, nk
)
(8.3)
. A = f (V, T, nk
)
(8.3)
dG = Vdp –SdT +
![]() . G = f (p, T, nk
)
(8.4)
. G = f (p, T, nk
)
(8.4)
8.2. Понятие химического потенциала.
m k a - химический потенциа л всегда является интенсивной характеристикой состояния компонента k в фазе a.
Химический потенциал k –компонента в фазе a показывает изменение любой характеристической функции при введении в систему (фазу) 1 моля k-вещества при постоянных естественных параметрах данной характеристической функции и неизменном количестве других компонентов (или при неизменном составе фазы), его можно также определить как работу, которую нужно затратить на введение в систему 1 моля k-вещества при указанных условиях .
m
k
=
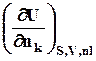 =
=
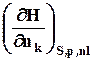 =
=
 =
=
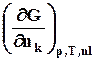 .
(8.5)
.
(8.5)
Наиболее часто используется именно последнее выражение химического потенциала через энергию Гиббса.
8.3. Интегрирование фундаментального уравнения Гиббса (8.1) по числу молей при постоянных температуре, давлении и составе. Будем увеличивать число молей в системе от нуля до n. В фундаментальном уравнении в качестве независимых переменных выступают экстенсивные величины, которые зависят от числа молей. Если n = 0, то и все экстенсивные переменные имеют в качестве нижнего предела 0.
![]() = T
= T
![]() – p
– p
![]() dV
+
dV
+ 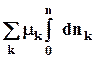
![]() (8.6)
(8.6)
U = TS – pV + S m k nk. (8.7)
H = U + pV = TS + S m k nk (8.8)
A = U –TS = -pV + S m k nk (8.9)
G = U + pV – TS = S m k nk (8.10)
Если система однокомпонентная , то уравнение (8.10) вовсе упрощается
G = m n . (8.11)
| m = G / n = G (8.12) Химический потенциал чистого вещества численно равен мольной энергии Гиббса. |
Отсюда вытекает важное следствие:
8.4. Уравнение Гиббса-Дюгема
Напишем полный дифференциал внутренней энергии из определения (8.7)
dU = TdS + SdT – pdV – Vdp +
![]() +
+ ![]() .
.
Подставим в него фундаментальное уравнение Гиббса (8.1):
TdS – pdV + ![]() = TdS + SdT – pdV – Vdp +
= TdS + SdT – pdV – Vdp + ![]() +
+ ![]()
SdT
–
Vdp
+
![]() = 0,
(8.13)
= 0,
(8.13)
или с учетом других видов полезной работы
SdT
–
Vdp
+
![]() + S
Xi
dYi
= 0.
(8.14)
+ S
Xi
dYi
= 0.
(8.14)
Уравнения (8.13) и (8.14) называются уравнениями Гиббса-Дюгема, неза-
висимыми переменными в них служат интенсивные характеристики. Оно показывает, что изменение интенсивных параметров системы связано между собой: изменение одного интенсивного параметра влечет за собой изменение другого, например, повышаете температуру – изменяются давление и химические потенциалы компонентов, и т.д. Таким образом для определения состояния системы нельзя использовать одни интенсивные параметры, нужно задать хотя бы один экстенсивный.
Если T,p = const, то уравнение Гиббса - Дюгема приобретает вид
![]() = 0 . (8.15)
= 0 . (8.15)
Это означает, что химические потенциалы веществ в системе, связаны между собой. Последнее уравнение играет большую роль в теории растворов.
8.5. Выражение химического потенциала компонента идеального газа
8.5.1 . Чистое вещество в закрытой системе ( n = const )
m = G / n = G .
dG = - S dT + V dp , при постоянной температуре dGT = V dp . (8.16)
Проинтегрируем последнее выражение от некоторого стандартного состояния до заданного с учетом уравнения Менделеева - Клапейрона
V = RT / p .
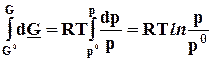
G
T
=
G
0
T
+
RT
ln
p
/
p
0
m
T
=
m
0
T
+
RT
ln
р,
![]() (8.17)
(8.17)
где р = p / p - приведенное давление, т.е. отнесенное к стадартному.
Так как p0 = 1 атм, то его часто опускают, но надо помнить, что под логарифмом не может стоять размерная величина, а только относительное давление ( или приведенное к стандартному давлению). При постоянной температуре химический потенциал пропорционален логарифму приведенного давления, а m 0 T - это стандартный химический потенциал идеального газа при заданной температуре ( и давлении = 1 атм)
8.5.2. Смесь газов
Рассмотрим процесс смешения: исходное состояние – 2 газа в стандартных условиях, конечное состояние смесь газов при той же температуре и том же общем давлении.
|
|
| pA + pB = p0 , T, nA , nB |
D
G A
= 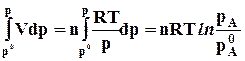 ;
D
GB
= nB
RT ln
pB
/pB
0
.
;
D
GB
= nB
RT ln
pB
/pB
0
.
D G = D G A + D GB = RT(nA ln pA /pA 0 + nB ln pB /pB 0 ) (8.18)
Используя уравнение (8.10), можно также записать
D GpT = nA ( m A - m A 0 ) + nB ( m A - m A 0 ). (8.19)
Сравнение уравнений (8.18) и (8.19) приводит к следующему выражению для химического потенциала компонента газовой смеси
m A = m A 0 + RT ln pA / p 0 и m B = m B 0 + RT ln pB / p 0 ,
т.е. химический потенциал компонента идеальной газовой смеси зависит от парциального давления этого компонента
m k = m k 0 + RT ln p k (8.20)
8.6. Реальные газы
8.6.1. Уравнение состояния реальных газов. Уравнение Ван-дер-Ваальса.
В отличие от уравнения состояния идеального газа уравнение Ван-дер-Ваальса включает поправки на объем самих молекул (коэффициент b - силы отталкивания) и притяжение молекул (член а/V 2 ) и имеет вид:
( p + ![]() ) (V
– b) = RT (8.21)
) (V
– b) = RT (8.21)
Уравнение кубическое – оно имеет 3 корня. Для изотермы Т (Рис 8.1) –это точки aoc . По мере повышения температуры эти точки сближаются, а при температуре Тк сливаются в одну точку К , называемую критической, в ней все корни вырождены – они имеют одно значение
V 1 = V 2 = V 3 = V крит .
При дальн.йшем повышении температуры два корня становятся мнимы-ми. При T Tкрит . газ нельзя перевести в жидкость изотермическим сжа-
|
Рис. 8.1. Состояния реального газа и изотермы Ван-дер-Ваальса
тием. При T Tкрит , напротив, газ переходит в жидкость при сжатии, и область под колоколом а b Кс (называемым бинодалью ) – это область двухфазная – жидкость и пар находятся в равновесии. Так, при сжатии по изотерме Т в точке c начинается конденсация пара, и дальнейшее сжатие в реальности приводит не к увеличению давления, а к увеличению количества жидкости – давление насыщенного пара постоянно.
Таким образом, реальный процесс конденсации пара изображается прямой линией ac , а не кривой ван-дер-Ваальса. Линия cg отвечает метастабильным неравновесным состояниям переохлажденного пара, а участок ae - перегретая жидкость. Область под кривой efKg (спинодаль) – нереализуемые состояния, когда с увеличением давления мольный объем газа увеличивается.
В критической точке изотерма имеет перегиб, т.е. первая и вторая производные от давления по объему равны 0. Эти уравнения дают связь между коэффициентами a и b уравнения Ван-дер-Ваальса, которые имеют индивидуальные значения для каждого газа и связаны с его критическими параметрами: Vкрит. = 3b ; Tкрит. = 8а/27 bR; pкрит. = a/27b2 . Поэтому если мы будем вместо обычных термодинамических параметров использовать их приведенные значения, т.е. отнесенные к критическим, то можно для всех газов написать одно более общее уравнение
(p + 3/j2 ) (3j-1) = 8 t, (8.22)
где p = р/ркрит . ; j = V/Vкрит . ; t=Т/Ткрит .. Это уравнение справедливо для различных веществ, имеющих сходный характер взаимодействия молекул. При критических параметрах все газы ведут себя сходным образом. Это справедливо и в точках равноотстоящих от критических, т.е. при одинаковых приведенных параметрах газы проявляют одни и те же свойства, такие состояния называют соответственными.
Кроме уравнения ван-дер-Ваальса, предложено много других состояний реальных газов, которые могут более точно описать процессы происходящие в них, но все они имеют сложный вид и работают в определенных границах параметров.
8.6.2. Химические потенциалы реальных газов.
Чтобы проинтегрировать уравнение (8.16) для реальных газов нужно было бы иметь аналитическую зависимость мольного объема такого газа от давления, но кубическое уравнение Ван-дер-Ваальса не имеет общего решения и нельзя представить общего вида такой зависимости, поэтому Льюисом был предложен совсем другой подход, который состоит в следующем: для реальных газов остается такая же форма термодинамических соотношений, что и для идеальных газов, но вместо давления используется другая переменная, называемая леутчестью, которая позволяет правильно описать свойства реальных газов.
Идеальные газы Реальные газы
D G = nRT ln p 2 / p 1 D G = nRT ln f 2 / f 1 (8.23)
G = G0 + RT ln p G = G0 + RT ln f (8.24)
m = m 0 + RT ln p m = m 0 + RT ln f (8.25)
8.6.3. Коэффициент летучести. Стандартные состояния.
![]()
![]() m
m
![]() 1
1
![]() m0
2
m0
2
![]()
![]() m*
m*
0 ![]() ln
p
ln
p
Рис.8.2. Зависимость химического потенциала идеального (1) и реального(2)газов от давления.
Химический потенциал идеального газа линейно зависит от логарифма давления (Рис.8.2). Для реального газа зависимость будет криволинейной. За стандартное состояние идеального газа принимают его состояние при давлении 1 атм (ln p = 0 ). Казалось бы на основании уравнения (8.25), что для реального газа – стандартным будет состояние при летучести, рав-ной единице (ln f = 0, точка m* ) . На самом деле стандартное состояние одно и то же для обоих газов: f0 = p0 = 1. Для того, чтобы придти к стандартному состоянию реальный газ нужно расширить по изотерме до бесконечно малого давления, где реальный и идеальный газы имеют одинаковые свойства, в том числе и химические потенциалы, а затем сжать до р = 1 по изотерме идеального газа. Такое сложное определение стандартного состояния позволяет все отклонения реального газа от идеального выразить через коэффициент летучести g , который связывает летучесть и давление:
f = g p , или g = f / p . (8.26)
Свойства реальных и идеальных газов сближаются по мере уменьше-ния давления lim f / p p ® 0 = 1. g p ® 0 = 1 . (8.27)
Таким образом, именно коэффициент активность выражает отклонение реального газа от идеального и связан с взаимодействиями, существующими в реальном газе. Отношение летучести к стандартному давлению называется активностью
a = f / f 0 = p / p 0 . (8.28)
8.6.4 . Методы определения летучести и коэффициента летучести .
8.6.4.1. Летучесть и коэффициенты летучести можно определять эксперименталь-но, измеряя мольные объемы реального газа в зависимости от давления. Эти объемы отличаются от молных объемов идеального газа на величину :
![]() =
V
ид
.
–
V
р
еал.
(8.29)
=
V
ид
.
–
V
р
еал.
(8.29)
V
реал.
=
V
ид
.
-
![]() =
RT
/
p
-
=
RT
/
p
-
![]() (8.30)
(8.30)
d
m
T
= dG
= RT d(ln
f) = V
dp = (RT/p -![]() ) dp,
(8.31)
) dp,
(8.31)
Проинтегрируем уравнение (8.31), приняв за нижний предел бесконечно малое давление, когда f 1 ® p 1 ® 0
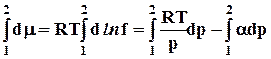
RT ln
(f2
/p1
) = RT ln
(p2
/p1
) - ![]() RT ln
p2
+ RT ln
g
= RT ln
p2
-
RT ln
p2
+ RT ln
g
= RT ln
p2
-
![]()
RT
ln
g
= -
![]() ;
ln
g
= - 1/
RT
;
ln
g
= - 1/
RT
![]() .
(8.32)
.
(8.32)
По экспериментальной зависимости величины от давления графически рассчитывают интеграл в уравнении (8.32) и таким образом находят ln g для разных давлений
![]()
![]()
![]()
![]()
![]() g
1.5 t
g
1.5 t
0.8 t
0.5 t
![]()
![]() 0 р p
0 р p
а) б)
Рис.8.3. Методы определения коэффициентов летучести: а) по уравнению 9.10, б) методом соответственных состояний.
8.6.4.2. Метод соответственных состояний
Как уже указывалось в разделе 8.6.1. разные газы ведут себя одинаково при одинаковых приведенных параметрах p, t. В справочниках имеются номограммы которые позволяют определить коэффициенты летучести разных газов по их приведенным параметрам, т.е. отнесенным критическим.
Таблица 8.1. Летучести и коэффициентов летучести азота при 0 С
| р, атм |
1 |
10 |
50 |
100 |
200 |
400 |
600 |
1000 |
| f |
0.9995 |
9.956 |
49.06 |
97.03 |
194.4 |
424.8 |
743.4 |
1.839 |
| g |
0.9995 |
0.9956 |
0.981 |
0.970 |
0.972 |
1.062 |
1.269 |
1.839 |
Лекция № 9
9. Химические реакции и химическое равновесие
9.1. Общее условие химического равновесия в закрытой системе
В химической реакции происходит изменение числа молей компонентов в соответствии со стехиометрическим уравнением 0 = S n k Ak . Этим системы с химическими реакциями напоминают открытые системы, которые обмениваются веществом с окружающей средой, поэтому полные дифференциалы характеристических функций следует записывать как для открытых систем, например, dG = - SdT + Vdp + S m k dnk .
При p,T = const dG р , Т = S m k dnk . (9.1)
Так же будут выглядеть дифференциалы других характеристических функций при постоянных значениях их естественных параметров. В самопроизвольных процессах при p , T = const энергия Гиббса должна убывать dG р,Т 0 , а в состоянии равновесия достигать минимального значения dG р,Т =0 . Следовательно, в самопроизвольной химической реакции при p , T = const S m k dnk 0 . Но если в истинно открытой системе изменения чисел молей веществ независимы друг от друга, то в закрытой системе с химической реакцией они связаны между собой и могут быть все выражены через химическую переменную
dnk / n k = d x и dnk = n k d x
dGpT = S m k n k d x .
В самопроизвольном процессе при p,T = const производная по степени протекания химической реакции должна убывать, а в состоянии химического равновесия равняться 0:
самопроизвольный процесс 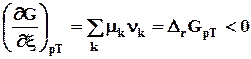 ; (9.2)
; (9.2)
химическое равновесие 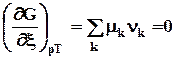 . (9.3)
. (9.3)
В принципе химическое равновесие можно выражать через любую характеристическую функцию, но наиболее просто это можно сделать через энергию Гиббса.
D r GpT = S m k n k = S G k n k = S G j n j - S n i G i = 0. (9.4)
Величина 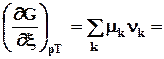 D
r
GpT
показывает изменение энергии Гиббса за 1 пробег (
D
r
GpT
показывает изменение энергии Гиббса за 1 пробег (![]() =1), т.е. при полном превращении реагентов в продукты в мольных количествах, соответствующих стехиометрическим коэффициентам, при р,T = const и заданном составе системы по сравнению с равновесным состоянием, для которого D
r
GpT
= 0. П
оэтому ее можно рассматривать как меру химической неравновесности системы,
а -
D
r
GpT
называют химическим сродством
. На графике 9.1 эта величина определяет угловой коэффициент наклона касательной. По мере увеличения химической переменной этот коэффициент уменьшается в связи с изменением состава реакционной смеси, достигая нуля при равновесии.
=1), т.е. при полном превращении реагентов в продукты в мольных количествах, соответствующих стехиометрическим коэффициентам, при р,T = const и заданном составе системы по сравнению с равновесным состоянием, для которого D
r
GpT
= 0. П
оэтому ее можно рассматривать как меру химической неравновесности системы,
а -
D
r
GpT
называют химическим сродством
. На графике 9.1 эта величина определяет угловой коэффициент наклона касательной. По мере увеличения химической переменной этот коэффициент уменьшается в связи с изменением состава реакционной смеси, достигая нуля при равновесии.
![]()
Рис. 9.1. Химическое сродство.
Поскольку нет возможности определить абсолютное значение энергии Гиббса какого-либо вещества, вводится понятие изменение ее в реакции образования (так же как энтальпии), т.е. получения данного соединения из простых веществ.
Тогда D r GpT = S D f G k n k = S D f G j n j - S n i D f G i = 0. (9.5)
Для простых веществ D f G = 0.
9.2. Уравнение изотермы химической реакции
9.2.1. Гомогенные газовые реакции
Уравнение изотермы химической реакции определяет изменение энергии Гиббса за один пробег (![]() =1) химической реакции при постоянной температуре и давлении. Для выявления факторов, влияющих на эту величину подставим в уравнение (9.4) выражения для химического потенциала
=1) химической реакции при постоянной температуре и давлении. Для выявления факторов, влияющих на эту величину подставим в уравнение (9.4) выражения для химического потенциала
m = m 0 + RT ln p (идеальный газ), m = m 0 + RT ln f / f (реальный газ)
D
r
GpT
=
S
(
m
0
k
+ RT ln
pk
)
n
k
=
S
m
о
k
n
k
+ RT ln
![]() =
=
D
r
GpT
=
D
r
GT
0
+ RT ln
![]() =
D
r
GT
0
+ RT ln
k
p
. =
D
r
GT
0
+ RT ln
=
D
r
GT
0
+ RT ln
k
p
. =
D
r
GT
0
+ RT ln
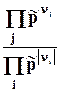 .
(9.6)
.
(9.6)
Для реальных газов вместо давления в уравнении изотермы будет стоять летучесть
D
r
GpT
=
D
r
GT
0
+ RT ln
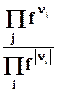 =
D
r
GT
0
+ RT ln
=
D
r
GT
0
+ RT ln
![]() =
D
r
GT
0
+ RT ln
k
f
.
(9.7)
=
D
r
GT
0
+ RT ln
k
f
.
(9.7)
Под знаком логарифма стоят произвольные парциальные давления, которые можно изменять как угодно, но которые поддерживаются постоянными. Проще всего это достигается при использовании проточной системы с массообменом, в которой устанавливается стационарный поток. Это означает, что в любом сечении трубчатого реактора поддерживается постоянный во времени состав реакционной смеси за счет того, что химическая реакция и массообмен компенсируют друг друга, хотя состав будет изменяться по длине реактора в связи с изменением степени превращения () вплоть до равновесного состава смеси, при котором и получают результат химической реакции. При этом через систему нужно пропустить такое количество исходной смеси, чтобы в итоге изменение химической переменной равнялось единице. Разница в энергии Гиббса между выбранным сечением и конечным состоянием, рассчитанная на единичный пробег, и будет отвечать величине, рассчитанной по уравнению изотермы D r GpT . Произвольные парциальные давления удобнее выражать в атмосферах, тогда они будут приведены к стандартному значению, чтобы под логарифмом стояла безразмерная величина.
9.2.2. Гетерогенные реакции
Такие реакции протекают на границе раздела фаз. Рассмотрим реакцию
FeO тв. + H 2газ = Fe тв. + H 2 O ж.
n -1 -1 1 1
D r GpT = m Fe + m H 2 O - m FeO - m H 2 = m Fe + m H 2 O - m FeO - m H 2 – RT ln pH 2
D r GpT = D r GpT – RT ln pH2 . (9.8)
m Fe = m Fe , m Fe О = m Fe О , . m H 2 O = m H 2 O .
Конденсированные фазы находятся в стандартном состоянии, поэтому под логарифмом в уравнении изотермы стоят давления только газообразных веществ. Для обычной температуры – только давление водорода, при высокой температуре - отношение парциальных давлений воды и водорода.
9.2.3. Влияние давления на направление реакции
Уравнение изотермы химической реакции позволяет определить, как изменяется направление реакции, если мы изменяем общее давление в системе
3/2 H 2 + 1/2 N 2 = NH 3 T = 500 K D r G 500 = 9.26 кДж.
Стандартное изменение энергии Гиббса положительно, т.е. при стандартных условиях реакция не идет в прямом направлении. Если сильно повысить давление до 600 атм, т.е. парциальное давление каждого газа будет cоставлять 200 атм, то знак D r G изменится
D
r
G
= D
r
G
+ RT ln![]()
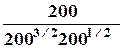 = 9260 - 8.314*500 ln 5.29 = -12600
Дж
.
= 9260 - 8.314*500 ln 5.29 = -12600
Дж
.
Соотношение между веществами осталось то же, но увеличение давления изменило направление реакции, так как в ней уменьшается число молей газообразных веществ D n газ = -1. В связи с этим химическое сродство этой реакции возрастает с ростом общего дваления в системе при неизменном относительном составе.
9.3. Закон действующих масс
9.3.1. Константа равновесия
D
GpT
=
D
GT
0
+
RT
ln
P
p
*
k
n
k
=
D
GT
0
+
RT
ln
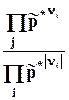 = 0
. (9.9)
= 0
. (9.9)
В состоянии равновесия при p,T = const D GpT = 0. Так как стандартное изменение энергии Гиббса зависит только от температуры, то и второе слагаемое в уравнении (9.10) также является функцией только температуры
- D GT 0 = RT ln P p* k n k = f (T) (9. 10)
Отношение равновесных парциальных давлений продуктов к давлению реагентов в степенях, соответствующих модулю стехиометрических коэффициентов, является величиной постоянной при Т= const и называется константой равновесия.
Kp
= 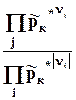 = P
p
*
k
n
k
=
f
(
T
)
и (9.11)
= P
p
*
k
n
k
=
f
(
T
)
и (9.11)
-
D
r
GT![]() =
RT
ln
Kp
(9.12)
=
RT
ln
Kp
(9.12)
Мы пришли к важнейшему выводу: константа равновесия однозначно определяется стандартным изменением энергии Гиббса в химической реакции, а уравнение изотермы можно представить в новом варианте
D r Gp Т = RT ln k / Kp , (9.13)
где k- отношение произвольных парциальных давлений продуктов и реа-гентов.
Для гетерогенных реакций в константу равновесия входят только равновесные парциальные давления газообразных веществ. Константа равновесия величина безразмерная, так как давления должны быть приведены к выбранному стандартному давлению. Таким образом мы получили термодинамический вывод закона действующих масс.
9.3.2. Способы выражения константы равновесия и взаимосвязь между ними
9.3.2.1. Идеальный газ при постоянном давлении и температуре
Парциальные давления компонентов газовой смеси можно выразить через их мольные доли и общее давление в системе р* к = робщ. х k , отсюда
Kp
=
P
p
*
k
n
k
= f
(
T
)
= 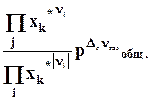 = Kx
p
общ
D
r
n
газ
, (9.14)
= Kx
p
общ
D
r
n
газ
, (9.14)
где Кх = P х* k n k = f ( T , p общ. )
Константа Кх , по сути своей уже не является истинной константой, так как зависит и от температуры, и от давления, но она не зависит от состава системы. Поэтому ее удобно использовать для определения влияния давления на равновесный состав смеси:
если D r n газ 0 , при р Кх ;
если D r n газ 0 , при р Кх , что соответствует принципу Ле-Шателье.
Реальный газ
В выражении константы равновесия реальных газов отношение равновесных парциальных давлений заменяется отношением их летучестей
Kf
=
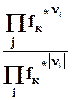 =
P
f*
k
n
k
= f(T) = Kp
P
g
k
n
k
.
(9.15)
=
P
f*
k
n
k
= f(T) = Kp
P
g
k
n
k
.
(9.15)
9.3.2.3. Идеальный газ при постоянном объеме и температуре
pV = nRT, p = nRT/V = cRT
Kp
= 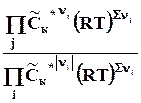 =
P
C*
k
n
k
(RT)
r
n
k
=
Кс
(RT)
r
n
k
= f(T),
(9.16)
=
P
C*
k
n
k
(RT)
r
n
k
=
Кс
(RT)
r
n
k
= f(T),
(9.16)
где r
![]() включает только газообразные вещества. Константу Кс
удобно использовать для газов, если реакцию проводят при постоянном объеме, а также для жидких растворов, так как в в этих случаях изменения количества веществ пропорциональны их концентрациям.
включает только газообразные вещества. Константу Кс
удобно использовать для газов, если реакцию проводят при постоянном объеме, а также для жидких растворов, так как в в этих случаях изменения количества веществ пропорциональны их концентрациям.
Лекция № 10
9.4. Влияние температуры на химическое равновесие
9.4.1. Вывод уравнения Вант-Гоффа
Для вывода потребуются 2 уравнения: уравнение Гиббса-Гельмгольца (7.30) и уравнение изотермы химической реакции – D r GT = RT ln Kp .
ln
Kp
= -
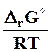 .
.
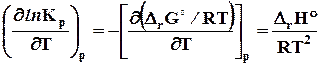 и (10.1)
и (10.1)
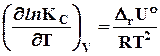 . (10.2)
. (10.2)
Эти уравнения называют изобарой (10.1) и изохорой (10.2) Вант-Гоффа.
9.4.2. Анализ уравнения Вант-Гоффа
Так как RT 2 0 . Изменение константы равновесия с ростом температуры определяется стандартной теплотой реакции.
Если D r H 0 реакция эндотермическая, то при T Kp ;
Если D r H 0 реакция экзотермическая, то при T Kp .
Такие изменения соответствуют принципу Ле-Шателье
9.4.3. Использование уравнения Вант-Гоффа
9.4.3.1. Определение D r H по температурной зависимости константы равновесия
а) две точки в небольшом интервале температур, D r H = с onst
 =
= 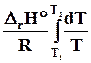
![]()
ln ![]() =
= 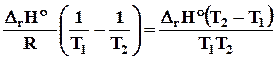
![]()
D
r
H
= R![]()
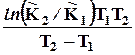 . (10.3)
. (10.3)
b) много точек в небольшом интервале температур (D r H = const ).
ln Kp = - D r H/R T + C (10.4)
Нужно построить график в координатах ln Kp = f (1/ T )
![]()
![]() ln
Kp
ln
Kp
![]() D
r
H 0
tg
a
= -
D
r
H / R
D
r
H 0
tg
a
= -
D
r
H / R
D r H 0
![]()
Рис. 10.1. Зависимость логарифма константы равновесия от 1/ T
В большом интервале температур зависимости могут быть криволинейными,
тогда нужно брать тангенс наклона касательной.
9.4.3.2. Определение константы равновесия при изменении температуры Известна константа равновесия при Т1 и D r H , требуется найти константу при другой температуре
a) малый интервал темпратур D r H 0 = const , из уравнения (10.3)
ln
K
2
–
ln
K
1
=
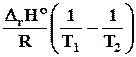 .
Откуда
.
Откуда
ln
K
2
=
ln
K
1
+
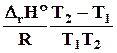 . (10.5)
. (10.5)
b) большой интервал температур D r H = f (T). В дифференциальное уравнение Вант-Гоффа (10.1) нужно подставить D r H = f ( T ) (4.19) и проинтегрировать
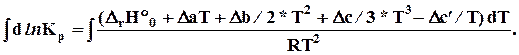
ln Kp = - D r H0 /RT + D a/R* ln T + D b/2R* T + D c/6R*T2 + D c’/2RT2 + const ( 10.6)
Зная константу равновесия при какой-либо температуре, можно найти постоянную интегрирования, а затем рассчитывать константу при любой температуре.
9.5. Расчетные и экспериментальные методы определения D r G 0 и констант равновесия
9.5.1. По справочным данным о стандартной энергии Гиббса для реакции образования веществ D f G . Так как нельзя определить абсолютное значение внутренней энергии, этого нельзя сделать и для энергии Гиббса, поэтому за уровень отсчета принимают стандартные состояния простых веществ, для которых энергию Гиббса полагают равной 0. В справочниках приводятся данные по энергиям Гиббса, отсчитанным от этого уровня. Тогда
D r G = S j n j D f G j - S i n i D f G i = S k n k D f G k (10.7)
9.5.2 . Если нет данных по D f G , то можно использовать справочные данные по стандартным теплотам образования и абсолютным энтропиям веществ
D r G = D r H – T D r S, (10.8)
где D r H = S j n j D f H j - S i n i D f H i = S k n k D f H k
и D r S = S j n j S j - S i n i S i = S k n k S k .
Эти уравнения показывают, что самопроизвольному протеканию реакции
(D r G 0) способствует ее экзотермичность ( D r H 0 ) и рост энтропии, однако обычно, если D r H 0 , то D r S 0 также, т.е. энергетический и энтропийный факторы действуют в разных направлениях, причем роль энтропийного фактора возрастает с повышением температуры:
D r H 0 и D r S 0 при D r H T D r S , тогда D r G 0 ; ln K 0 ; K 1;
при D r H T D r S , тогда D r G 0 ; ln K 0; K 1.
9.5.3. По измерению полезной работы
- D r G T , p = ( W ’) max (7.16), например, в электрохимии можно измерить ЭДС гальванического элемента в обратимом процессе
D r G T , p = - E F z , где
где E – стандартная ЭДС элемента, F – число Фарадея, z – количество электронов в уравнении окислительно-восстановительной реакции.
9.5.4. Экспериментальное определение констант равновесия.
- D r G T = RT ln Kp . Положительное значение D r G T не означает, что реакция вообще не может идти, она не может протекать в стандартных условиях, когда реагенты и продукты присутствуют в системе под давлением 1 атм. Но в отсутствии продуктов в начале реакции, реакция, конечно, пойдет до состояния равновесия и задача экспериментатора найти равновесную степень превращения, равновесный выход или состав равновесной смеси при заданных исходных условиях. Каждая реакция требует своего подхода для определения этого равновесного состояния системы, но в любом случае нужно составить материальный баланс реакции и выразить изменение какой-либо измеряемой величины через химическую переменную. Для газовых реакций в которых изменяется число молей газообразных веществ, такой измеряемой величиной может быть реакционный объем при постоянном давлении. Разберем это на примере реакции
NO 2 = NO + 1/2 O 2 . Если nk 0 = 1, то x = a
n k -1 1 1/2
nk0 1 0 0
nk * 1 - x* = a* 1/2a*
=1 - a* , nk * = 1+1/2a*
Nk
*
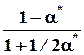
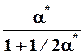
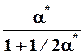
pk
*
p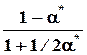 p
p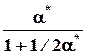 p
p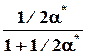
где nk 0 и nk * - начальные и равновесные числа молей веществ, Nk * - равно-весные мольные доли, а pk * – равновесные парциальные давления веществ,
pk * = p . Nk * = p nk * / S nk * , р – общее давление в системе.
Кр
= 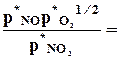
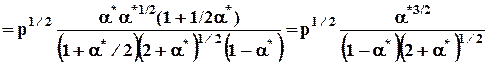 . (10.9)
. (10.9)
V * / V 0 = n * / n 0 = (1 + 1/2 a * ) ; ( V * - V 0 )/ V 0 = 1/2 a * .
Измеряя относительное увеличение объема, можно найти равновесную степень превращения и константу равновесия, и, наоборот, зная констан-ту, легко найти равновесный выход в любых условиях.
9.5.5. По известным константам равновесия некоторых реакций, можно найти константу равновесия для любой линейной комбинации этих реакций.
FeO + C = Fe + CO K = ?
![]() 1 FeO + CO = Fe + CO2
K1
D
r
G1
1 FeO + CO = Fe + CO2
K1
D
r
G1
1/2 2 C + O2 = 2 CO K2 D r G2
-1 CO + 1/2 O2 = CO2 K3 D r G3
D r G = D r G1 + 1/2 D r G2 - D r G3 ;
ln K = ln K1 + 1/2lnK2 – ln K3 ; K = K1 K2 1/2 K3 -1 .
Константа равновесия реакции равна произведению констант равновесия реакций в степенях соответствующих коэффициентам, с которыми эти реакции входят в линейную комбинацию, составляющую данную.
9.5.6. Приведенный потенциал Энтальпия и энтропия химической реакции слабо зависят от температуры, а энергия Гиббса – сильно, так как включает член T D r S . Поэтому в справочниках можно найти для разных веществ так называемый приведенный потенциал
Ф(Т) = ( G Т – H 0 )/ T , (10.10)
который изменяется с ростом температуры значительно медленнее, а значения Т даются с интервалом в 100 . В формуле 10.10 H 0 – теплота реакции образования при абсолютном нуле, которая также приводится в таблицах приведенных потенциалов веществ .
Отсюда для каждого вещества G / T = Ф(Т) + H 0 / T , и применяя оператор D r , находим
ln Kp = - D r G Т / RT = –1/ R [ D r Ф (Т) + D r H 0 / T ]. (10.11)
Таким образом, для расчета константы при равновесия при любой таблич-ной температуре Т нужно найти в справочнике две термодинамические характеристики для компонентов системы Ф(Т) + H 0 . Для уточнения констант при любой температуре можно воспользоваться уравнением Вант-Гоффа, определив теплоту реакции в заданном интервале по табличным значениям разности теплот образования при температуре Т и абсолютном нуле ( H Т – H 0 ) , приводяшейся в этих же таблицах.
D r НТ = D r Н0 + D r ( H Т – H 0 ). (10.12)
9.5.7. Статистические расчеты констант равновесия
Все термодинамические функции выражаются через статистические суммы веществ
Q = S i gi exp(- e i /kT)
![]() m
k
= G
k
= -RT ln Q/NA
+ U
0
.
(10.13)
m
k
= G
k
= -RT ln Q/NA
+ U
0
.
(10.13)
Kc
=
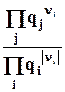 exp
(-
D
r
U
0
0
/
RT
)
(10.14)
exp
(-
D
r
U
0
0
/
RT
)
(10.14)
Q / V = q - статистическая сумма единицы объема
Оглавление
Курс лекций по физической химии
Учебно–методическое пособие
Подписано в печать ……………..…Формат 60х84\16. Бумага писчая.
Отпечатано на ризографе. Уч. изд. листов Тираж 100 экз. Заказ №…
Лицензия на издательскую деятельность
ИД № 03507 (рег. № 003792) код 221
Московская государственная академия тонкой химической технологии им. М.В. Ломоносова
Издательско-полиграфический центр.
119571 Москва, пр. Вернадского 86.