Курсовая работа
СОДЕРЖАНИЕ: Исследование сложной электрической цепи постоянного тока методом узловых потенциалов. R1=130 Ом R2=150 Ом R3=180 Oм R4=110 Oм R5=220 Oм R6=75 Oм R7=150 OмИсследование сложной электрической цепи постоянного тока методом узловых потенциалов.
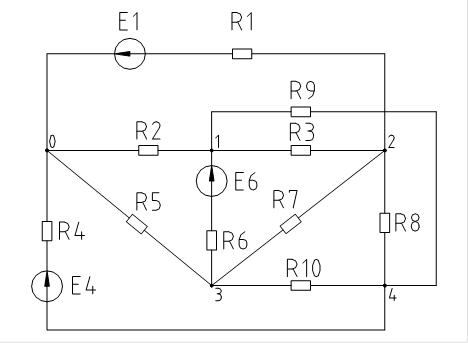
R1=130 Ом
R2=150 Ом
R3=180 Oм
R4=110 Oм
R5=220 Oм
R6=75 Oм
R7=150 Oм
R8=75 Oм
R9=180 Oм
R10=220 Oм
E1=20 В
E4=5.6 В
E6=12 В
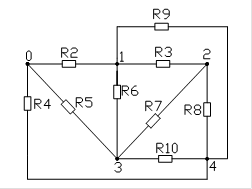
1. Расчет узловых потенциалов.
Заземляем 0й узел, и относительно него рассчитываем потенциалы остальных узлов.
Запишем матрицу проводимостей для этой цепи:
Y=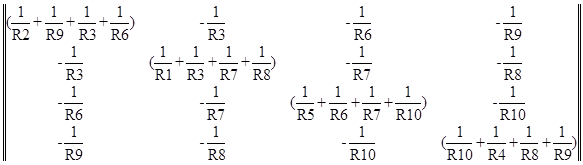
После подстановки значений:
Y=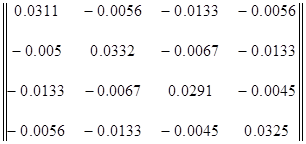
Составляем матрицу узловых токов:
I=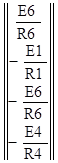
По методу узловых потенциалов мы имеем уравнение в матричном виде:
Y – матрица проводимостей;
U – матрица узловых потенциалов;
I – матрица узловых токов.
Из этого уравнения выражаем U:
Y-1 – обратная матрица;
Решаем это уравнение, используя математическую среду Matlab: U=inv(Y)*I
inv(Y) – функция ищущая обратную матрицу.
U=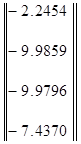
Зная узловые потенциалы, найдем токи в ветвях:
i1
=
= -0.0768; i2
=
= -0.0150; i3
=
= -0.0430;
i4
=
= -0.0167; i5
=
= -0.0454; i6
=
= 0.0569;
i7
=
= 4.228110-
5
; i8
=
= 0.0340; i9
=
= -0.0288;
i10
=
= 0.0116
2. Проверка законов Кирхгофа.
Первый закон
для 0го узла : i4 +i2 -i5 -i1 =0
для 1го узла : i2 +i6 -i3 -i9 =0
для 2го узла : i3 +i7 -i8 -i1 =0
для 3го узла : i10 -i7 -i6 -i5 =0
для 4го узла : i8 +i4 +i9 -i10 =0
Второй закон
1й контур : i1 R1+i2 R2+i3 R3=E1 20=20
2й контур : i2 R2-i6 R6+i5 R5=-E6 -12=-12
3й контур : i4 R4-i8 R8-i3 R3-i2 R2=E4 5.6=5.6
4й контур : i3 R3+i8 R8+i10 R10+i6 R6=-E6 -12=-12
5й контур : i3 R3-i7 R7+i6 R6=E6 12=12
6й контур : i9 R9-i8 R8-i3 R3=0 0=0
3. Проверка баланса мощностей в схеме
Подсчитаем мощность потребителей:
P1 =i1 2 R1+i2 2 R2+i3 2 R3+i4 2 R4+i5 2 R5+i6 2 R6+i7 2 R7+i8 2 R8+i9 2 R9+i10 2 R10+E4i4 = 2.2188
Сюда включёна мощность Е4 так как он тоже потребляет энергию.
Подсчитаем мощность источников:
P2 =E1i1 +E6i6 =2,2188
P1 -P2 =0
4. Метод эквивалентного генератора.
Рассчитаем ток в ветви с максимальной мощностью, методом эквивалентного генератора.
Сравнивая мощности ветвей видим, что максимальная мощность выделяется в первой ветви, поэтому уберём эту ветвь и для получившейся схемы рассчитаем Uxx и Rэк .
Расчёт Uxx методом узловых потенциалов:
Матрица проводимостей:
Y=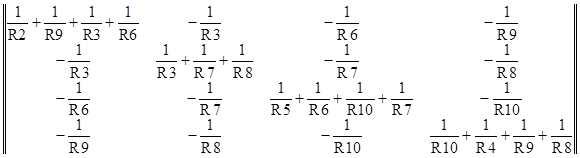
Матрица узловых токов:
I=
По методу узловых потенциалов находим:
=
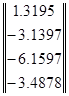
Но нас интересует только разность потенциалов между 0ым и 3им узлами: U30 =Uxx =-6.1597.
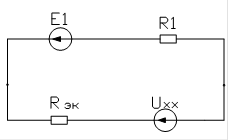
I1
=
=
=-0.0686
Где эквивалентное сопротивление находится следующим образом:
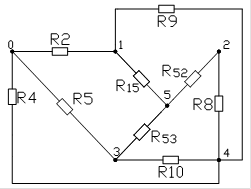
123 :123
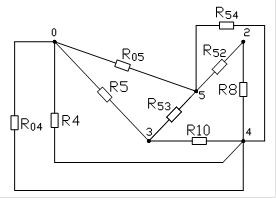
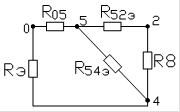
:054 054 :054 054
:024 024
При переходе от : используется формулы преобразования: 
, а при переходе :: 
, две остальные формулы и в том, и в другом случаях получаются путем круговой замены индексов.
Определим значение сопротивления, при котором будет выделяться максимальная мощность. Для этого запишем выражение мощности на этом сопротивлении: 
. Найдя производную этого выражения, и приравняв её к нулю, получим: R=Rэк
, т.е. максимальная мощность выделяется при сопротивлении нагрузки равном внутреннему сопротивлению активного двухполюсника.
5.
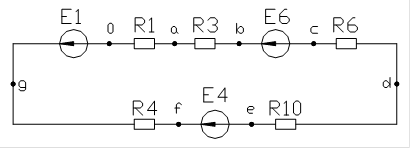Построение потенциальной диаграммы по контуру.
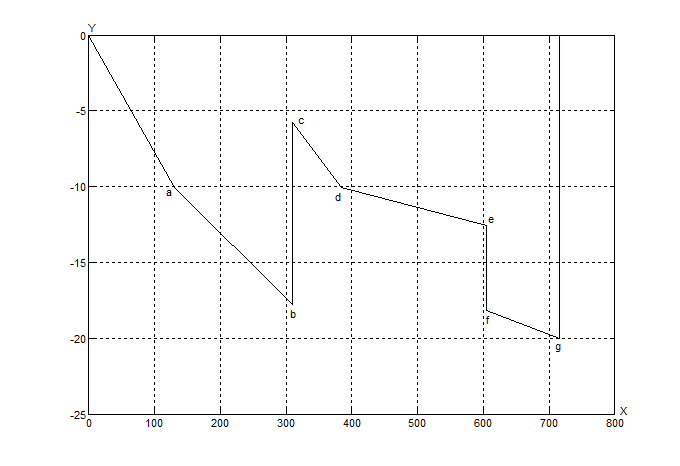По оси X откладывается сопротивление участка, по оси Y потенциал соответствующей точки.
Исследование сложной электрической цепи переменного тока методом контурных токов.
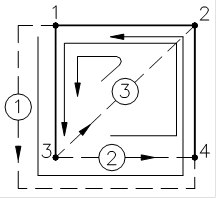
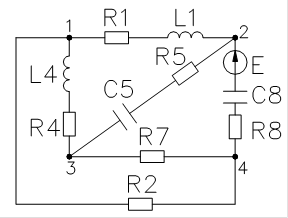
Переобозначим в соответствии с графом:
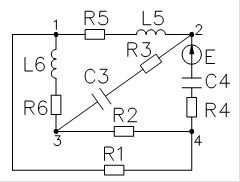
R1=110 Ом L5=50 млГ С4=0.5 мкФ
R2=200 Ом L6=30 млГ С3=0.25 мкФ
R3=150 Ом
R4=220 Ом E=15 В
R5=110 Ом w=2pf
R6=130 Ом f=900 Гц
1. Расчет токов и напряжений в схеме, методом контурных токов.
Матрица сопротивлений:
Z=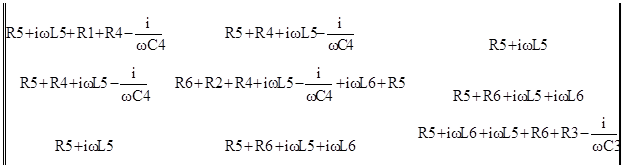
=
=102
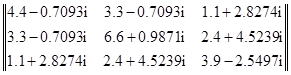
Матрица сумм ЭДС, действующих в ком
контуре: Eк
=
По методу контурных токов: Ix
=Z-1
Eк
=
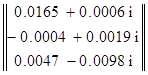
Действующие значения: Ix
=
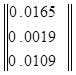
Выражаем токи в ветвях дерева: I4 =I1 +I2 = 0.0161+0.0025i I4 =0.0163
I5 =I1 +I2 +I3 =0.0208-0.0073i I5 =0.0220
I6 =I2 +I3 =0.0043-0.0079i I6 =0.0090
Напряжения на элементах:
UR1
=I1
R1=1.8162 UL5
=I5
wL5=6.2327 UC3
=I3
=7.6881
UR2
=I2
R2=0.3883 UL6
=I6
wL6=1.5259 UC4
=I4
=5.7624
UR3 =I3 R3=1.6303
UR4 =I4 R4=3.5844
UR5 =I5 R5=2.4248
UR6 =I6 R6=1.1693
2. Проверка баланса мощностей.
Активная мощность:
P=I1 2 R1+I2 2 R2+I3 2 R3+I4 2 R4+I5 2 R5+I6 2 R6=0.1708
Реактивная мощность:
Q=I5
2
wL5+I6
2
wL6-I32
=-0.0263
Полная мощность:
S=
=0.1728
С другой стороны:
Активная мощность источника:
P=EI4
cos(arctg
)=0.1708
Реактивная мощность источника:
Q=EI4
sin(arctg)=-0.0265
Полная мощность источника:
S=EI4 =0.1728
3. Построение векторной диаграммы и проверка 2го закона Кирхгофа.
Для 1го контура:
I1
R1+I4
R4+I4
+I5R5+I5282.7433i-E=0.0088-0.0559i
Для 2го контура:
I2
R2+I4
R4+I4
+I5
282.7433i+I5
R5+I6
169.6460i+I6
R6=0.0088- 0.0559i
Для 3го контура:
I5
R5+I6
169.6460i+I6
R6+I3
+I3
R3+I5
282.7433i=-0.0680-0.0323i
Векторная диаграмма:
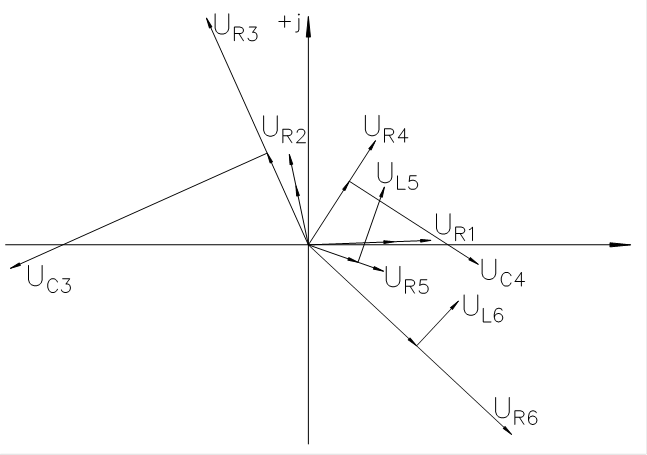
Топографическая диаграмма для 1го контура:
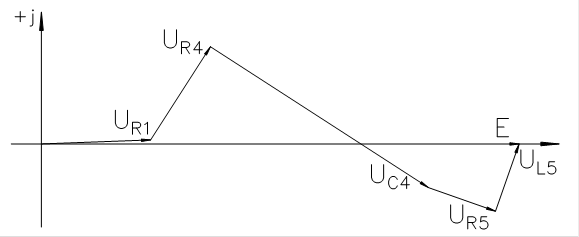
Топографическая диаграмма для 2го контура:
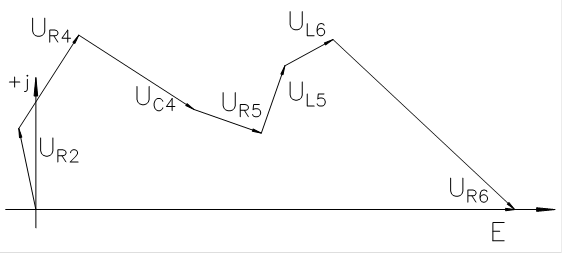
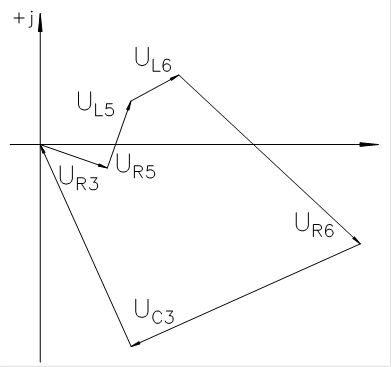
Топографическая диаграмма для 3го контура:
Исследование сложной электрической цепи постоянного тока методом узловых потенциалов. 1
1. Расчет узловых потенциалов. 1
2. Проверка законов Кирхгофа. 2
3. Проверка баланса мощностей в схеме_ 3
4. Метод эквивалентного генератора. 3
5. Построение потенциальной диаграммы по контуру. 4
Исследование сложной электрической цепи переменного тока методом контурных токов. 5
1. Расчет токов и напряжений в схеме, методом контурных токов. 6
2. Проверка баланса мощностей. 6
3. Построение векторной диаграммы и проверка 2го закона Кирхгофа. 7