Квантовая природа света

СОДЕРЖАНИЕ: Волновые свойства света, обна­руживаемые в явлениях интерференции и дифракции, и корпуску­лярные свойства света, проявляющиеся при фотоэффекте и эф­фекте Комптона, кажутся взаимно исключающими друг друга. Однако такие противоречия существовали лишь в классиче­ской физике. Квантовая теория полностью объясняет с единых позиций все свойства света.

. Волновые свойства света, обна­руживаемые в явлениях интерференции и дифракции, и корпуску­лярные свойства света, проявляющиеся при фотоэффекте и эф­фекте Комптона, кажутся взаимно исключающими друг друга. Однако такие противоречия существовали лишь в классиче­ской физике. Квантовая теория полностью объясняет с единых позиций все свойства света. Характерной чертой квантовой теории света является объяснение всех явлений, в том числе и тех, ко­торые ранее казались объяснимыми лишь с позиций волновой теории. Например, явления интерференции и дифракции света квантовая теория описывает как результат перераспределения фотонов в пространстве.

Распределение фотонов в пучках света при интерференции и дифракции описывается статистическими законами, дающими те же результаты, что и волновая теория. Однако торжество современной квантовой теории в объяснении всех световых явле­ний не означает, что никаких волн в природе нет.

Волновые свойства электрона. Полному отказу от волновых представлений о природе света препятствуют не только сила традиции, удобство волновой теории и трудность современной квантовой теории. Есть и более серьезная причина. В 1924 г. французский физик Луи де Б рой ль впервые высказал идею, согласно которой одновременное проявление корпускулярных и волновых свойств присуще не только свету, но и любому дру­гому материальному объекту. Эта идея была лишь теоретиче­ской гипотезой, так как в то время наука не располагала экспери­ментальными фактами, которые бы подтверждали существование волновых свойств у элементарных частиц и атомов. В этом зак­лючалось существенное отличие гипотезы де Бройля о волновых свойствах частиц от гипотезы Эйнштейна о существовании фото­нов света, выдвинутой им после открытия явления фотоэффекта.

Гипотеза де Бройля существовании волн материи была детально разработа­на, и полученные из нее следствия могли быть подвергнуты экспериментальной проверке. Основное предположение де Бройля заключалось в том, что любой материальный объект обладает волновыми свойствами и длина волны связана с его импульсом таким же соотношением, ка­ким связаны между собой длина свето­вой волны и импульс фотона. Найдем выражение, связывающее импульс фото­на р с длиной волны света . Импульсфотона определяется формулой:

P=mc(1)

Л. Де Бройль

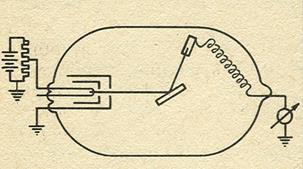
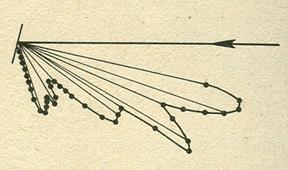
рис.1 рис. 2

Из уравнения

Е= m с² = hv (2)

можно определить массу фотона:

(3)

Учитывая это, можно формулу преобразовать так:

(4)

Отсюда получаем для длины световой волны формулу:

(5)

Если это выражение справедливо, как предположил де Бройль, для любого материального объекта, то длина волны тела мас­сой т, движущегося со скоростью v, может быть найдена так:

(6)

Первое экспериментальное подтверждение гипотезы де Брой-ля подучили в 1927 г. независимо друг от друга американские физики К. Д. Дэвиссон и Л. X. Джермер и английский физик Д. П. Томсон. Дэвиссон и Джермер изучали отражение электрон­ных пучков от поверхности кристаллов на установке, схема кото­рой изображена на рисунке 1. Перемещая приемник электро­нов по дуге окружности, центр которой находится в месте паде­ния электронного пучка на кристалл, они обнаружили сложную зависимость интенсивности отраженного пучка от угла рис. 2. Отражение излучения только под определенными углами означа­ет, что это излучение представляет собой волновой процесс и его избирательное отражение есть результат дифракции на атомах кристаллической решетки. По известным значениям постоянной кристаллической решетки и dугла дифракционного максимума можно по уравнению Вульфа — Брэггов

2d sin=k

вычислить длину волны дифрагировавшего излучения и сопоставить ее с дебройлевской длиной волны электронов , вы­
численной по известному ускоряющему напряжению U:

Вычисленная таким образом из опытных данных длина волны совпала по значению с дебройлевской длиной волны.

Интересны результаты другого опыта, в котором пучок электронов направлялся на монокристалл, но расположение при­емника и кристалла не изменялось. При изменении ускоряющего напряжения, т. е. скорости электронов, зависимость силы тока через гальванометр от ускоряющего напряжения имела вид, представленный на рисунке 3. Электронный пучок испытывал наиболее эффективное отражение при скоростях частиц, удовлет­воряющих - условию дифракционного максимума.

Последующие эксперименты полностью подтвердили правиль­ность гипотезы де Бройля и возможность использования урав­нения (6) для расчета длины волны, связанной с любым материальным объектом. Обнаружена дифракция не только эле­ментарных частиц (электрон, протон, нейтрон), но и атомов.

Выполнив расчеты длины дебройлевской волны для различных материальных объектов, можно понять, почему мы не замечаем в повседневной жизни волновых свойств окружающих нас тел. Их длины волн оказываются столь малыми, что проявление волновых свойств невозможно обнаружить. Так, для пули массой 10 г, движущейся со скоростью 660 м/с, длина дебройлевской волны равна:

Дифракция электронов на решетке кристалла никеля стано­вится заметной лишь при таких скоростях движения электронов, при которых их дебройлевская длина волны становится сравни­мой с постоянной решетки.

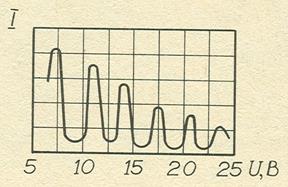
рис. 3 рис. 4

При этом условии дифракционная картина, получаемая от электронного пучка, становится подоб­ной картине дифракции пучка рентгеновских лучей с такой же длиной волны. На рисунке 4 представлены фотографии дифрак­ционных картин, наблюдающихся при прохождении пучка света (а) и пучка электронов (б) у края экрана.

Гипотеза де Бройля и атом Бора. Гипотеза о волновой при­роде электрона позволила дать принципиально новое объяснение стационарным состояниям в атомах. Для того чтобы понять это объяснение, выполним сначала расчет длины дебройлевской волны электрона, движущегося по первой разрешенной круговой орбите в атоме водорода. Подставив в уравнение (6) выраже­ние для скорости электрона на первой круговой орбите, получим:

(7)

Это значит, что в атоме водорода, находящемся в первом стационарном состоянии, длина дебройлевской волны электрона в точности равна длине его круговой орбиты! Для любой другой орбиты с порядковым номером п получаем:

(8)

Этот результат позволяет выразить постулат Бора о стацио­нарных состояниях в такой форме: электрон вращается вокруг ядра неопределенно долго, не излучая энергии, если на его орби­те укладывается целое число длин волн де Бройля.

Такая формулировка постулата Бора соединяет в себе одно­временно утверждение о наличии у электрона волновых и корпус­кулярных свойств, отражая его двойственную природу. Соедине­ние волновых и корпускулярных свойств в этом постулате проис­ходит потому, что при расчете длины волны электрона исполь­зуется модуль скорости , полученный при расчете движения электрона как заряженной частицы по круговой орбите радиуса r.

Взаимные превращения света и вещества. Глубокое единст­во двух различных форм материи — вещества в виде различных элементарных частиц и электромагнитного поля в виде фотонов — обнаруживается не только в двойственной корпускулярно-волновой природе всех материальных объектов, но главным образом в том, что все известные частицы и фотоны взаимно превращаемы.

Самый известный пример взаимных превращений частиц — это превращение пары электрон — позитрон в два или три гамма-кванта. Этот процесс наблюдается при каждой встрече электрона с позитроном и называется аннигиляцией (т.е. исчезновением). При аннигиляции строго выполняются законы сохранения энер­гии, импульса, момента импульса и электрического заряда (элект­рон и позитрон обладают равными зарядами противоположного знака), но материя в форме вещества исчезает, превращаясь в материю в форме электромагнитного излучения.

Процесс, обратный аннигиляции, наблюдается при взаимо­действии гамма-квантов с атомными ядрами. Гамма-квант, энер­гия которого превышает энергию покоя Ео=2m₀ c² пары элект­ рон — позитрон , может превратиться в такую пару.

Таким образом, материя не только многообразна в своих формах, но и едина в своей сущности. Разделение материаль­ных объектов на отдельные группы и виды условно и относи­тельно.

Скачать архив с текстом документа