Лекции по статистике

СОДЕРЖАНИЕ: Основные понятия описательной статистики, графическое изображение статистических данных, числовые характеристики одномерных признаков.

Введение.

Термин “статистика” (“status”в переводе с латинского означает государство) появился в 17 веке.

Первоначально статистика возникла как наука количественного описания происходящих в обществе процессов с использованием “меры, веса и числа”. В современной жизни слово “статистика” имеет два основополагающих значения: во-первых, оно обозначает сами числа или данные. Под этим термином обычно понимают некоторую информацию об окружающем нас мире, не интересуясь способом ее получения, представляющую потенциальный интерес и упорядоченную определенным образом. Примерами данных являются результаты переписи населения, сведения о концентрации вредных веществ в воздушном бассейне города, соответствующие друг другу курсы валют и так далее.

Все возрастающее количество накапливаемых данных порождает проблемы возможного сокращения их количества без существенной потери полезной информации, потенциально в них заложенной. Поэтому, во-вторых, под статистикой понимают науку извлечения полезной информации из множества данных.

Существует несколько определений статистики - наука принятия разумных решений перед лицом неопределенности. Для принятия решения в отношении исследуемого объекта мы должны:

1. иметь о нем информацию, т.е. располагать определенным образом собранными и сгруппированными результатами наблюдения;

2. иметь методы анализа и обработки статистических данных в зависимости от цели исследования.

Таким образом, статистика - наука о методах организации сбора, систематизации и обработки статистических данных с целью удобного из представления, правильной интерпретации и получения научных и практических выводов.

Статистика может быть представлена в виде двух составных частей:

1. описательной статистики, позволяющей с помощью специальных методов осуществить удобное представление данных для последующего анализа в виде частотных распределений, графических изображений и различных характеристик.

2. математической (теории принятия статистических решений)

Зарождение описательной статистики отмечается уже в 2200 году до н. э. в. Китае. В дальнейшем, практическая статистика в административных и военных целях находит применение в Египте, Персии, Римской Империи, подтверждая свое название. Значительно позднее, на базе теории вероятностей, зародилась математическая статистика, благодаря трудам выдающихся математиков Я..Бернулли, П. Лапласа, К. Гаусса.

Общей чертой сведений, составляющих статистику служит то, что в каждом конкретном случае объектом статистического изучения является статистическая совокупность, состоящая из качественно однородных единиц, но отличающихся по каким-то другим признакам. Качественная однородность элементов совокупности определяется исходя из цели исследования. Генеральной совокупностью называются все изучаемые однородные объекты, выборка - специально организованная часть генеральной совокупности.

Задача получения необходимой информации решается с помощью двух взаимно дополняющих принципов: выборочного метода и свертки информации. Первый предусматривается отказ от генеральной совокупности в пользу выборки, второй - заменяет всю выборку несколькими числами (ее характеристиками). Статистические характеристики различают как для генеральной совокупности, так и для выборки. Необходимо сделать несколько замечаний по применению статистических методов:

1. результаты статистического анализа могу противоречить действительности, это происходит тогда, когда исследователь не понимает проблемы либо применяемых статистических методов.

2. существует возможность умышленно вводить в заблуждение с помощью статистики.

3. в последнее время специалисты стараются применят все более тонкие статистические методы. Такой практики следует избегать, так как цель анализа не показать знание сложных аналитических методов, а правильно решить задачу.

Статистические методы в современной жизни находят свое применение в самых разнообразных областях: в экономике (исследования рынка и производства, контроль качества продукции, подбор кадрового персонала, предсказания конъюнктуры рынка и т.д.), в управлении (аппарат которого нуждается в информации о народонаселении, совокупном общественном продукте, внешней торговле). Без применения стат. методов практически невозможно никакое социально-научное исследование. С появлением ЭВМ, статистика проникает и в медицину, биологию, психологию и другие науки.

В зависимости от учреждений, использующих статистические методы, различают официальную и неофициальную статистику. Под официальной статистикой понимают статистические исследования и меры по сбору информации, предпринимаемые в соответствии с правительственными распоряжениями. К неофициальной статистике относят исследования, проводимые в фирмах, институтах общественного мнения и на предприятиях.

Тема 1. Основные понятия описательной статистики.

Совокупность - множество элементов, обладающих некоторыми общими свойствами, существенными для их характеристики.

Единица совокупности - элемент совокупности, подлежащий наблюдению. Признак - свойство элементов совокупности. Самым важным различием признаков является их классификация на контролируемые (входные) и признаки отклика (выходные). Например, уровень финансовых вложений в производство является входным признаком, а продуктивность - выходным. Второй особенностью наблюдений является математический характер соответствующего признака, в частности, тип множества допустимых значений, который принимает признак в процессе наблюдения. В этом смысле признаки делятся на качественные и количественные. Качественные признаки это те признаки, которыми объект либо обладает, либо не обладает. К ним относятся: пол, цвет волос или национальность и т.д. Такие признаки не являются физически измеримыми, однако они могут быть двузначными или многозначными.

Количественные признаки являются измеримыми и определяются путем измерений, взвешиваний и подсчетов. В соответствии с этим различают дискретные и непрерывные количественные признаки. Дискретные признаки могут принимать лишь изолированные значения, отличающиеся друг от друга на некоторую конечную величину. Примером таких признаков является академическая система успеваемости: 5 - отлично, 4 - хорошо и т.д. Совокупность возможных значений, среди которых изменяется (варьируется) дискретный признак называется системой вариант. Отдельное значение системы называется вариантой.

Непрерывные признаки могут принимать любые значения на некотором числовом интервале, отличающиеся друг от друга на сколь угодно малую величину. К таким признакам относятся, например, возраст, рост и вес человека.

Множество допустимых значений признаков как качественного, так и количественного вида характеризуются типом шкалы в которой они изменяются. различают три основных типа шкал: номинальная или шкала наименований, порядковая и количественная, количественная в свою очередь подразделяется на интервальную, шкалу отношений и абсолютную шкалу.

В номинальной шкале все элементы совокупности классифицированы и классы обозначены номерами. То, что номер оного класса больше или меньше другого, еще не говорит о свойствах элементов, за исключением того, что они различаются. Номинальная шкала может быть категоризированной или нет. В категоризированной шкале исследователю заранее известны уровни, принимаемые признаком. Например, раса, цвет глаз, автомобильные номера, клинические диагнозы и т.д.

В порядковой шкале соответствующие значения чисел, которые присваиваются элементам совокупности, отражают количество анализируемого признака. Однако равные разности числе не означают равных разностей в количествах признака. Например, твердость минералов, награды за заслуги, военные ранги, уровень интеллекта и т.д.

В интервальной шкале существует единица измерения ( масштаб), при помощи которой объекты можно не только упорядочить, но и приписать им числа так. чтобы равные разности чисел, присвоенные объектам, отражали бы равные различия в количествах измеряемого признака. Нулевая точка интервальной шкалы выбирается произвольно и не указывает на отсутствие признака. Например, календарное врем, шкалы температур и т.д.

В шкале отношений, числа, присвоенные элементам совокупности, обладают всеми интервальными признаками, но помимо этого существует абсолютный нуль, который свидетельствует об отсутствии анализируемого признака. Отношение чисел, присвоенных элементам в процессе измерений. отражает количественное отношение наличия признака. Например, рост, вес, объем, урожайность.

Абсолютная шкала является безразмерной шкалой отношений.

Тема 2. Вариационные ряды.

Пример 1.

Приведем оценки 45 студентов по курсу статистика в порядке сдачи экзамена:

5 3 3 4 2 4 4 3 5 4 4 5 5 4 4

3 3 3 2 5 5 4 4 4 3 4 3 4 5 4

4 4 4 3 3 4 3 4 3 2 3 2 3 3 3

При таком представлении информации трудно делать какие-либо выводы об успеваемости. Произведем группировку данным путем подсчета количества различных оценок.

оценки	2	3	4	5
количество	4	6	8	7

Как видим, вместо 45 чисел осталось 8, при этом повысилась информативность таблицы, более 50% студентов сдали предмет на хорошо и отлично. Данный пример показывает, что эти данные лучше сгруппировать, то есть разделить их на однородные группы по некоторому признаку. Благодаря группировке данные приобретают систематизированный вид. Если данные систематизированы по времени, то моделью группировки будет временный ряд. Если же по любому другому признаку - то ряд распределения. А для количественных признаков - вариационный ряд.

Пусть Х - одномерный количественный признак и в результате n его измерений наблюдалось n его значений x(1),x(2).....x(n), среди которых могут быть одинаковые. Эти значения называют вариантами. Пуст среди имеющихся n вариант имеется k различных.Причем x1 встречается m1 раз, xk - mk раз. Понятно, что .

Определение.

Вариационным рядом называется последовательность различных вариант. записанных в возрастающем порядке вместе с соответствующими частотами. Вариационный ряд обычно записывается в одном из видов: в таблице с частотами mi, через относительные частоты Wi=mi/n. В зависимости от типа признака различают дискретные и интервальные вариационные ряды. В зависимости от объема исходных данных и области допустимых значений одномерного количественного признак, частотные распределения также подразделяются на дискретные и интервальные. Если различных вариант очень много (более 10-15), то эти варианты группируют, выбирая определенное число интервалов группировки и получая таким образом интервальное частотное распределение. Алгоритм группировки массива данных состоит из следующих шагов:

1. находят минимальную и максимальную варианты

2. весь диапазон значений признака [Xmin,Xmax] разбивают на к интервалов одинаковой длины .

Число К обычно берется в пределах 10-15. Редки случаи, когда требуется более 25 и менее 8 группировок. Существуют формулы для определения “оптимального” значения К и построения таким образом оптимального распределения частот. Формула Старджеса . Для больших n эта формула дает оценку снизу для К.

3. находят граничные точки каждого из интервалов и т.д.

4. подсчитываем число вариант Mi, попавших в интервал , причем варианты, попавшие на границы интервалов, относят только к одному из интервалов, результат заносят в таблицу .

Пример 2.

Приведем вариационный ряд почасовой оплаты 303 рабочих промышленности

Xi	2.49	2.50	2.51	2.52	2.53	2.54	2.55	2.56	2.57	2.58	2.59	2.6	2.61
Mi	1	4	1	1	0	3	2	0	3	2	1	8	1

2.62	3	2.72	9	2.82	11	2.92	6	3.02	2	3.12	0	3.22	1	3.32	1
2.63	0	2.73	3	2.83	3	2.93	2	3.03	0	3.13	0	3.23	0	3.33	0
2.64	5	2.74	10	2.84	4	2.94	4	3.04	3	3.14	2	3.24	0	3.34	2
2.65	7	2.75	11	2.85	7	2.95	8	3.05	4	3.15	4	3.25	3	3.35	2
2.66	3	2.76	4	2.86	5	2.96	5	3.06	2	3.16	2	3.26	1	3.36	0
2.67	2	2.77	2	2.87	3	2.97	2	3.07	0	3.17	0	3.27	0	3.37	1
2.68	3	2.78	9	2.88	8	2.98	3	3.08	2	3.18	2	3.28	0
2.69	2	2.79	5	2.89	4	2.99	1	3.09	0	3.19	1	3.29	0
2.70	14	2.8	22	2.90	16	3.0	9	3.10	7	3.20	4	3.30	4
2.71	4	2.81	3	2.91	3	3.01	1	3.11	0	3.21	0	3.31	0

Построим для данного ряда интервальное частотное распределение.

1. X min = 2,49 Xmax=3,37

2.

Для удобства вычислений возьмем К=10. и т.д.

Для наглядного представления дискретных частотных распределений могут применяться вертикальные линии. Каждый из примеров можно рассматривать либо как выборку, либо как генеральную совокупность. Обычно данные собирают и анализируют для практических результатов.

пример.

Абсолютное частотное распределение прибыли 100 крупных межнациональных компаний, базирующихся в США за 1988 г.

Класс компании, размер прибыли, млн.$	Число компаний в классе
-1500-0	3	|||
0-500	41	|||| |||| |||| |||| |||| |||| |||| |||| |||| |||| |
500 - 1000	32	|||| |||| |||| |||| |||| |||| |||| ||||
1000 - 1500	9	|||| |||| |
1500 - 2000	6	|||| ||
2000 - 2500	6	|||| ||
2500 - 5500	3	|||

3. Графическое изображение статистических данных.

Обычно табличное распределение частот дополняют его графическим представлением. Схематически все множество графических представлений статистических данных разделяют на два класса: диаграммы и линейные изображения. К классу линейных графиков относятся полигон, кумулятивная кривая, кривая концентрации, огива.

Полигоном частот называют ломаную, отрезки которой соединяют точки

Иногда крайние точки соединяют с точками, имеющими нулевую ординату.

пример. (с оценками)

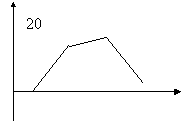
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки .

Замечание.

Если на ось абсцисс наносить возможные исходы событий, а на ось ординат - вероятности этих исходов, то ломаная линия, характеризующая изменение вероятностей различных исходов событий при испытаниях называется полигоном распределения вероятностей.

Кумулятивная кривая (кривая сумм) - ломаная, составленная по последовательно суммированным, т.е. накопленным частотам или относительным частотам. При построении кумулятивной кривой дискретного признака на ось абсцисс наносятся значения признака, а ординатами служат нарастающие итоги частот. Соединением вершин ординат прямыми линиями получают кумуляту. При построении кумуляты интервального признака, на ось абсцисс откладываются границы интервалов и верхним значениям присваивают накопленные частоты. Кумулятивную кривую называют полигоном накопленных частот.

Если на ось ординат нанести значение признака, а накопленные частоты - на ось абсцисс, то получим кривую, называемую огивой.

Кривой концентрации или кривой Лоренца называют кривую относительной концентрации суммарного значения признака. Пусть имеется вариационный ряд, отражающий, например, частотное распределение семей по их доходам, где число (процент) семей с доходом . Тогда общий доход

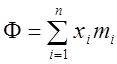- суммарный доход.

Относительный накопленный доход

Построение кривой Лоренца осуществляется следующим образом: по оси абсцисс откладывают накопленные относительные частоты, а по оси ординат накопленный относительный доход.

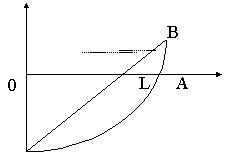
1. Если доход распределяется по семьям равномерно, то кривая Лоренца описывается прямой ОВ. Это означает, что 10% семей получают 10% общего дохода и т.д.

2. абсолютная (полная) концентрация задается ломаной ОАВ. Это означает, что преобладающее число семей ( например 99%) совсем не имеют дохода и только 1% имеет весь суммарный доход.

3. В промежуточных случаях между этими экстремальными графиками кривая Лоренца описывает увеличение концентрации дохода в руках небольшой части семей при приближении ее графика к кривой ОАВ, при уменьшении концентрации ее график располагается ближе к прямой ОВ. Концентрация определяется площадью области ОСВ, чем больше величина площади, тем сильнее концентрация.Площадь S можно найти по формуле средних прямоугольников. В качестве меры концентрации используется коэффициент Джини: .

пример.

4.ДИАГРАММЫ.

Диаграмма ( от греческого diagramma - изображение, чертеж, рисунок) - это графическое изображение, наглядно показывающее соотношение между сравниваемыми величинами. Диаграммы бывают различных видов: полосовые (ленточные), столбиковые, квадратные, круговые, секторные, фигурные, радиальные, знак Варзара.

1. Полосовые - особенно наглядны при сравнении величин, связанных между собой в единое целое. Ширина полос должна быть одинаковой. По длине полосы разбиваются на части, пропорциональные изображаемым величинам.

пример 1.

Данные по классификации безработных в США (средние по месяцам)

Год	ищут работу	частично занятые	нет работы
1989	6.5	4.9	0.9
1990	6.9	5.1	0.8
1991	8.4	6.0	1.1

2. Основным видом столбиковых диаграмм являются гистограммы.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основанием которых служат частотные интервалы длины h, а высоты равны отношению Mi/h - плотность частоты. Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними на расстоянии Mi/h проводят отрезки параллельные основанию. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основанием которых случат частичные интервалы длиной h, а высоты равны Wi/h.

Гистограмма относительных частот - аналог плотности распределения непрерывной случайной величины. Иногда высоты прямоугольников в гистограмме не делят на h, но указывают над столбиками значение высоты и над осью ординат пишут, что ее значение надо делить на h. Такую гистограмму называют масштабированной.

пример.

3. при построении квадратных и круговых диаграмм площади квадратов или кругов выражают изображаемые величины.

пример. Сравнение грузооборота. В СНГ в 1990 г. грузооборот железнодорожного транспорта составил 3505,2 тыс. т, морского - 853.9, автомобильного - 458.9. (Вычислить корни квадратные - сторона квадрата)

4. Круговые секторные диаграммы применяют для графического изображения составных частей целого. Для из построения необходимо изображаемые данные выразить в градусах, т.к. 1% составляет 3,6 градусов, то соответствующие показатели для определения центральных улов надо умножить на 3.6. Чтобы легче различать сектора используют различную раскраску или штриховку.

5. радиальные - они строятся в полярной системе координат и используются для изображения признаков, периодически изменяющихся во времени (в большинстве своем сезонных колебаний). Вычисляется среднее арифметическое, затем строится окружность радиуса равного среднему арифметическому. Данная окружность делится на нужное число секторов (обычно 12) и на каждом радиальном направлении откладываются точки в соответствии со значениями Xi.

6. фигурные диаграммы строятся 2 основными способами: данные изображаются либо фигурами различных размеров, либо разной численностью фигур одинакового размера. Второй способ чаще используется, каждая фигура содержит определенное число единиц признака и сравнение осуществляется по числу фигурок. При этом допускается дробление знака до половины.

7. Stem leaf- данные можно представить в виде десятков и единиц, где десятки - это стебли, единицы - лепестки.

8. Диаграмма “знак Варзара” названа в честь русского статистика. С помощью данной диаграммы можно изображать многомерные признаки на плоскости посредством прямоугольников с разным соотношением между основанием и высотой. Одна из компонент признака изображается основанием прямоугольника, вторая его высотой, третья - равная произведению двух других размером получившейся площади.

примеры.

Тема 4. Числовые характеристики одномерных признаков.

С целью обеспечения обработки частотных распределений и свертки информации, заключенной в статистических данных, вариационные ряды описывают с помощью определенных числовых характеристик. Такими характеристиками для одномерных статистических рядов являются следующие:

1. характеристики положения

2. характеристики рассеяния

3. характеристики формы;

5. СРЕДНИЕ ВЕЛИЧИНЫ. СТЕПЕННЫЕ СРЕДНИЕ.

Схематично средние величины можно представить следующим образом:

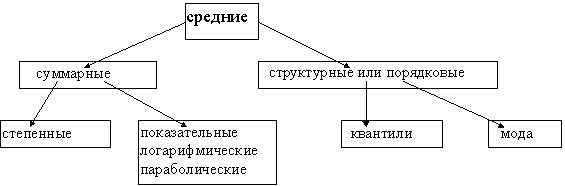
Степенная средняя

Эта формула задает не взвешенную или простую среднюю степенную. Она применяется для не сгруппированных данных. Для сгруппированных данных применяется следующая формула

Рассмотрим различные значения q.

q =-1 получаем среднее гармоническое

q =0 среднее геометрическое

q = 1 среднее арифметическое

q = 2 среднее квадратичное

Справедливо следующее неравенство для средних величин

Рассмотрим среднее арифметическое:

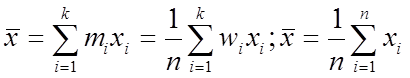
Отметим наиболее важные свойства среднего арифметического:

если из всех значений признака вычесть некоторую константу С,

1. если все значения признака умножить на с, то и среднее умножается на С.

2. пусть исходные данные представлены следующим образом , т.е. данные разбиты на q групп . Взвешенное среднее арифметическое из групповых или частотных средних будет равняться общей средней.

4. сумма взвешенных отклонений значений признака от общей средней арифметической равна 0: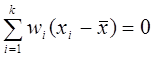

5. сумма квадратов взвешенных отклонений значений признака от меньше аналогичной суммы от любой другой меры положения

, разность между этими суммами равна .

Рассмотрим среднее гармоническое q=-1.

Свойства среднего гармонического:

1. взвешенная гармоническая из групповых гармонических равна общей гармонической .

Применение того или иного вида весов зависит от представления значений признака.

Примеры.

Таким образом, если между показателями существует обратная зависимость как например между числом изготовленных деталей и затратами времени на одно изделие, то надо использовать среднее гармоническое. А если между показателями существует прямая зависимость, например между индивидуальными зарплатами и фондом зарплат, то применяется среднее арифметическое.

Рассмотрим геометрическое среднее:

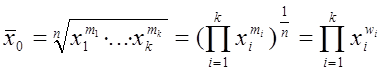
Вычислим предел:

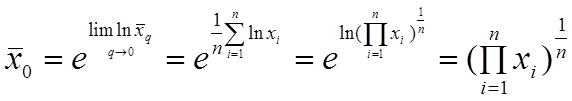
6. Свойства среднего геометрического:

1. общее среднее геометрическое может быть найдено по формуле .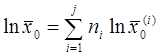

2. если кроме признака х рассмотреть признак у со значениями у(1), у(2),......,, то имеем

3. если есть несколько совокупностей , то имеем

Среднее геометрическое применяется для расчета среднего коэффициента или среднего темпа роста

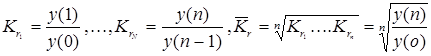
пример.

Пусть известно, что за 5 лет выпуск промышленной продукции предприятия вырос в 1.5 раза, тогда средний ежегодный коэффициент роста , т.е. 108,4 %, а средний ежегодный прирост равен 8,4%.

Среднее квадратическое q=2.

Обычно применяются, если в качестве берутся отклонения значений признака от среднеарифметических .

Если n=30, то применяется исправленное среднеквадратичное отклонение .

7.Структурные (порядковые) характеристики.

Квантили - порядковые характеристики, то есть значения признака, занимающие определенное место в ранжированной совокупности (упорядоченной).

Медиана.

Медиана - значение изучаемого признака, приходящееся на середину ранжированной совокупности.

При вычислении медианы интервального вариационного ряда, сначала находят медианный интервал , где h - длина медианного интервала. Для этого можно использовать кумулятивное распределение частот или относительных частот. Медианному интервалу соответствует тот, в котором содержится накопленная равная 1/2.

Внутри найденного интервала расчет медианы производится по формуле:

, где - кумулятивная частота интервала, предшествующего медианному, - относительная частота медианного инетрвала.

Сумма взвешенных абсолютных отклонений вариант от медианы меньше аналогичной суммы отклонений вариант от любой другой меры положения вариационного ряда.

Это свойство можно использовать при проектировании оптимального (в некотором смысле) расположения остановок общественного транспорта, складских помещений, бензозаправок и т.д.

пример.

Прибыль компаний: Ме=500 +500*(50-44)/(76-44)=593.75 млн. Это означает, что 50% компаний имеет прибыль меньше 593.75 млн.

Оценки студентов: Ме=4

Квартили.

Квартили - порядковые характеристики, отделяющие четверти ранжированных совокупностей.

1 квартиль или нижний отделяет четверть ранжированной совокупности снизу и вычисляется по формуле:

(для интервального)

Медиану можно рассматривать как второй квартиль.

Верхний квартиль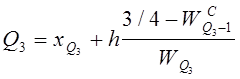

Мода.

Мода - наиболее часто встречающееся в совокупности значение признака. Для дискретного вариационного ряда мода определяется по частотам вариант и соответствует варианте с максимальной частотой. При определении моды обычно применяют следующие соглашения:

1. если все значения вариационного ряда имеют одинаковую частоту, то говорят, что этот вариационный ряд не имеет моды.

2. если две соседних варианты имеют одинаковую доминирующую частоту, что мода вычисляется как среднее арифметическое этих вариант.

3. если две не соседних варианты имеют одинаковую доминирующую частоту, то такой вариационный ряд называется бимодальным.

4. если таких вариант более двух, то ряд - полимодальный.

В случае интервального вариационного ряда с равными интервалами модальный интервал определяется по наибольшей частоте, а при неравных интервалах - по наибольшей плотности.

При равных интервалах мода внутри модального интервала может определяться по следующей формуле:

Данная формула получена исходя из допущения, что в модальном и двух соседних интервалах кривая распределения представляет собой параболу второго порядка. Тогда мода находится как вершина параболы. Для графического определения моды используют 3 соседних столбца гистограммы (самый высокий и 2 прилегающих к нему).

При вычислении моды в формуле можно использовать не только относительные, но и другие частоты.

пример.

Прибыль 100 компаний - Мо=0+500*(41-1)/(41-1+41-32)=408.16 млн.

Оказывается, по расположению средней арифметической, моды и медианы можно судить о форме распределения. Если оно симметричное, то все три величины равны.

В практике мода и медиана иногда используются вместо средней арифметической или вместе с ней. Фиксируя средние цены товаров или продуктов на рынке записывают наиболее часто встречающуюся цену на рынке (моду цены).

Робастные характеристики для оценки среднего арифметического.

В ряде случаев в изучаемой совокупности имеется небольшое число элементов с чрезвычайно большим или чрезмерно малым значением исследуемого признака.

В этих случаях в дополнение к среднему арифметическому целесообразно вычислить моду и медиану, которые в отличие от среднего не зависят от крайних, не характерных для совокупности значений признака. Мода и медиана относятся к классу так называемых “робастных характеристик”, т.е. не чувствительных к аномальным значениям признака. Рассмотрим робастные характеристики, применяемые для оценки среднего арифметического:

1. усеченное среднееарифметическое порядка

Пусть имеем ряд значений признака, упорядоченный в возрастающем порядке

, упорядоченный в возрастающем порядке. Пусть первые x(1),...,x(m) - аномально маленькие, x(n-m+1),...,x(n) - аномально большие.

- указывает долю отбрасываемых значений признака.

2. среднее по Виндору

Отличается от усеченного тем, что аномальные значения признака не отбрасываются, а полагаются крайним значениям, принимаемым на обработку.

x(1)=x(2)...=x(m)=x(m+1)

x(n)=x(n-1)=...=x(n-m+1)=x(n-m)

примеры.

8.Характеристики рассеяния.

Средняя величина признака, а также его мода и медиана в двух совокупностях могут быть одинаковыми. но в одном случае значения признака могут мало отличаться от среднего, а в другом эти значения могут быть велики.

пример.

Пусть имеются данные о стаже работы в 2 бригадах.

стаж	1	2	3	4	5	6	7	8	9	10	средн.
1 бр.	1	2	3	3	4	9	10	12	13	15	7.2
2 бр.	6	6	7	7	7	7	8	8	18	8	7.2

Простейшим из показателей является вариационный размах R=Xmax-Xmin. Размах выборки дает лишь самое общее представление о размерах вариации, так как показывает насколько отчаются друг от друга крайние значения, но не указывают насколько велики отклонения вариант друг от друга внутри этого промежутка. Более точным будет такой показатель, который учитывает отклонение каждой из вариант от средней величины.

Выделяют среднее линейное отклонение , либо среднеквадратичное отклонение .

Если объем выборки невелик, то в качестве оценки дисперсии рассматривают .

пример.

Для вычисления дисперсии можно использовать формулу .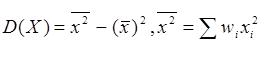

Основные свойства дисперсии:

1.

2.

3.

4. , то есть дисперсия принимает минимальное значение среди всевозможных взвешенных квадратов отклонений значений признака от любой другой меры положения а.

5. правило сложения дисперсий

Пусть ряд значений признака состоит из j однородных групп: x(1),...,X(n1),...X(n1+n2),...X(n),n=n1+n2+...+nj. Обозначим дисперсии групп D1,...Dj/

Надо найти общую дисперсию.

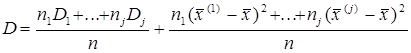
, т.е. общая дисперсия равна сумме внутригрупповой и внешне групповой дисперсий.

Таким образом общая дисперсия равна взвешенной сумме групповых дисперсий и взвешенной сумме квадратов отклонений групповых средних от общей средней. Первое слагаемое выражает величину дисперсии внутри частей совокупности, а второе- различие между этими частями.

пример.

Каждая из перечисленных дисперсий имеет вполне определенный смысл: общая дисперсия показывает величину вариации зарплаты, которая вызвана всеми факторами, влияющими на размер зарплаты. (число обслуживаемых станков, различия в опыте и т.д.) Групповые дисперсии показывают величину вариации, которая вызвана многими причинами кроме различий в числе обсуживаемых станков, так как внутри группы все рабочие обслуживают одинаковое количество станков. Средняя из групповых вариаций вызвана не различиями в числе обслуживаемых станков по всему числу рабочих, различия по числу станков.

Чем больше межгрупповая дисперсия по сравнению , тем больше влияние группировочного признака на величину исследуемого признака.

Если группировать рабочих внутри каждой группы по другому признаку, оказывающему влияние на заработок, например по уровню квалификации, то можно из внутригрупповых дисперсий выделить дисперсию, показывающую величину вариации, вызванной вторым группировочным признаком и дисперсию остаточную, характеризующую вариацию за счет всех причин, кроме 2 группировочных признаков. Теоретически такую комбинационную группировку можно продолжать до тех пор, пока не будут исчерпаны все причины, воздействующие на исследуемый признак. Общая дисперсия в этот случае будет представлена как сумма дисперсий, характеризующих вариацию, вызванную каждой из причин.

Кроме абсолютных для характеристики совокупности значений признаков применяются относительные показатели.

Коэффициент вариации .

Используется для сравнения размеров вариации в вариационных рядах с различными средними, а также для сравнения вариаций разных показателей в оной и той же совокупности. Он отражает состояние между вариацией выборки и ее центром.

1. =30% - выборка имеем довольно большую степень концентрации относительного среднего.

2. 30%==100% - степень концентрации допустимая.

3. =100% - делается вывод о неоднородности выборки.

пример.

Реже используются следующие коэффициенты:

1. Коэффициент вариации по размаху

2. Коэффициент вариации по среднему линейному отклонению

3. Квартильное отклонение .

9.Характеристики формы распределения вариационного ряда.

Существуют 2 основных характеристики: коэффициент ассиметрии и коэффициент эксцессов, которые характеризуют соответсвенно скошенность и крутость распределения.

Моментом порядка р распределения вариационного ряда называется

В зависимости от значения а общая схема моментов разбивается на 3 подсистемы.

1. а=0, получаем систему начальных моментов

2. а=x, получаем систему центральных моментов

3. а=с=const, обычно С близкое к середине вариационного ряда. Получаем систему условных моментов. Она применяется для упрощения расчетов.

Центральные моменты 3 и 4 порядков используются для характеристики ассиметрии и эксцесса распределения вариационного ряда.

10.Сравнение эмпирического и теоретического распределений вариационных рядов.

1. дискретные вариационные ряды

Пусть имеется вариационный ряд. Предположим, что признак Х распределен по некоторому вероятностному закону Р.

Р:

х	х1	х2	....	xk
р	p1	p2	.....	pk

По теоретическому распределению Р можно построить так называемое выравнивающие или теоретические частоты . Если отличия между теоретическими и эмпирическими частотами небольшое, то можно считать, что Х распределен по закону Р.

2. критерий согласия Пирсона

Объективную оценку близости эмпирических частот к теоретическим можно получить с помощью определенных критериев близости, называемых критериями согласия. Существует множество таких критериев. Критерий Пирсона основан на следующем:

.

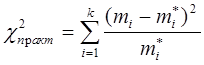Существуют значения (табличные) для соответствующего числа степеней свободы К и уровня значимости . По таблице находятся

K=k-1-r, где r - число общих характеристик теоретического распределения, принятых равными соответствующим эмпирическим.

11.Оценивание параметров распределений по выборке. Доверительные интервалы.

1. требования к оценкам

Пусть требуется изучить количественный признак генеральной совокупности. Допустим из теоретических соображений удалось установить какое именно распределение имеет признак. Естественна задача оценки параметров этого распределения.

Требования к оценкам:

1. несмещенность или асимптотическая несмещенность

2. состоятельность

Требование состоятельности применяется к большим объемам.

3. эффективность

Эффективной называют оценку, которая при заданном объеме выборки n имеет min дисперсию.

2. надежность оценок

Оценку, определяемую одним числом называют точечной. При выборках малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольших объемах выборки пользуются интервальными оценками, которые определяются 2 числами - концами интервала. Эти оценки позволяют установить точность и надежность оценок.

Пусть =const, тем точнее определяет , чем меньше (-). Если есть величина 0, (-), то чем меньше , тем точнее оценка.

- надежность оценки. Обычно надежность задается наперед =95-99%. Величину называют уровнем значимости.

, интервал - доверительный. Концы этого интервала - случайные величины и называются доверительными границами, они могут меняться от выборки к выборке. Говорят, что наш доверительный интервал с вероятностью покрывает .

Скачать архив с текстом документа