Магнитное поле Земли

СОДЕРЖАНИЕ: Ковчегин Игорь 8 Межпланетное магнитное поле Если бы межпланетное пространство было вакуумом, то единственными магнитными полями в нем могли быть лишь поля Солнца и планет, а также поле галактического происхождения, которое простирается вдоль спиральных ветвей нашей Галактики. При этом поля Солнца и планет в межпланетном пространстве были бы крайне слабы.

Межпланетное магнитное поле

Если бы межпланетное пространство было вакуумом, то единственными магнитными полями в нем могли быть лишь поля Солнца и планет, а также поле галактического происхождения, которое простирается вдоль спиральных ветвей нашей Галактики. При этом поля Солнца и планет в межпланетном пространстве были бы крайне слабы.

На самом деле межпланетное пространство не является вакуумом, а заполнено ионизованным газом, испускаемым Солнцем (солнечным ветром[1] ). Концентрация этого газа 1-10 см^-3 , типичные величины скоростей между 300 и 800 км/с, температура близка к 10⁵ К (напомним, что тем­пература короны 210⁶ К).

Поскольку газ солнечного ветра почти полностью иони­зованный, то его электропроводность очень велика (10² Мо/см). Проводники с высокой проводимостью имеют особенность сопротивляться изменению магнитного поля. Другими словами, проникновение магнитного поля в такой проводник невозможно.

Движущийся солнечный ветер будет уносить солнечное магнитное поле в межпланетное пространство. Так как по­ток плазмы начинается в короне Солнца (или ниже нее), то в солнечном ветре имеются магнитные поля. Величина магнитных полей на Солнце составляет от 1 до 1000 Гс.

Поток солнечной плазмы «выметает» из внутренней части солнечной системы планетные и галактические маг­нитные поля. Солнечный ветер будет «гнать» галактическое поле перед собой до тех пор, пока не будет достигнуто динамическое равновесие между давлением солнечного вет­ра и давлением галактической среды. Это происходит на расстоянии от 10 до 100 астрономических единиц[2] (а. е.). Следовательно, межпланетное пространство ограничено полостью в галактической среде, размеры которой дают верхнюю границу величины солнечно-межпланетного маг­нитного поля. Силовые линии магнитного поля солнечного ветра про­стираются в межпланетное пространство за орбиту Земли, при этом один их конец находится на Солнце. Характе­ристики солнечного ветра и межпланетных магнитных по­лей нерегулярны и асимметричны из-за волокнистой струк­туры короны, нерегулярностей магнитных полей в фото­сфере и т. д.

Радиальная компонента межпланетного магнитного поля В_r должна уменьшаться обратно пропорционально квадрату расстояния от Солнца (т. е. как r^-2 ). Она может быть выражена через величи­ну радиальной компоненты поля на поверхности Солнца. Если на Солнце магнитное поле равно Br₀ = 0,5 Гс, то на расстоянии 1 а.е. поле .B_r »1g.

Истечение плазмы из Солнца происходит таким образом, что плазма просто отталкивает силовые линии поля и покидает Солнце в ра­диальном направлении. Если бы Солнце не вращалось, то такое радиальное истечение плазмы привело бы к тому, что силовые линии магнит­ного поля были бы также радиальны и параллельны дви­жению частиц. Поскольку Солнце вращается, то маг­нитное поле приобретает поперечную компоненту (в пло­скостях, перпендикулярных оси вращения) и силовые ли­нии магнитного поля становятся спиральными.

Направление спирального поля можно оценить, если предположить, что один конец силовой линии закреплен на Солнце и вращается вместе с ним. Тогда частицы, ко­торые непрерывно испускаются данной областью вращаю­щейся короны, будут двигаться в экваториальной плоскости по спиралям Архимеда. (Это напоминает работу вращаю­щегося поливального устройства). Таким образом, меж­планетное магнитное поле приобретает и поперечную ком­поненту B_j . Можно оценить, что вблизи орбиты Земли угол спирали с радиусом составляет около 45° и радиаль­ная и поперечная компоненты B_j =B_r =1g.

Первые измерения магнитных полей за пределами маг­нитосферы Земли были проведены на спутнике «Пионер-1» в октябре 1958 г. Они позволили установить существова­ние и положение области перехода от внешней части гео­магнитного поля к межпланетному пространству. Эти результаты были подтверждены измерениями на других ИСЗ. Экспериментально было установлено, что имеются значительные нерегулярности, наложенные на спиральное межпланетное поле.

Спутниковые измерения межпланетного магнитного поля выявили тесную связь между величиной магнитного поля, перпендикулярного оси вращения аппарата (по­перечной составляющей В_^ ), и значением магнитного индекса К или А.

Перед началом и в период геомагнитных бурь вели­чина В_^ увеличивается на порядок и приобретает более нерегулярный характер, чем в спокойные периоды.

Это объясняется тем, что плазма из возмущенных об­ластей на Солнце может уносить в межпланетное про­странство более интенсивные и более нерегулярные поля. А это приводит к появлению нерегулярностей в спокойном межпланетном поле, что подтверждают измерения на спут­никах.

Обнаружена также прямая корреляция между изме­нениями межпланетного поля по данным спутников и сол­нечной активностью. По этим данным была оценена средняя скорость распространения возмущения, равная ~1000км/с.

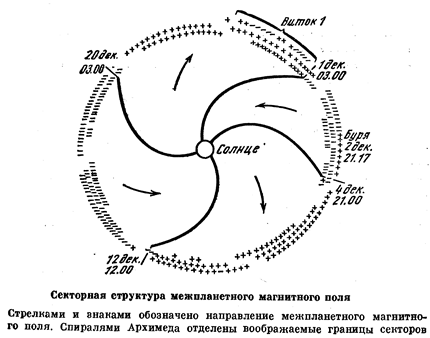
Вектор межпланетного магнитного поля имеет радиаль­ную составляющую В_r , направленную или от Солнца (знак +), или к Солнцу (знак –). Межпланетное про­странство разделено на чередующиеся спиральные секто­ры, в каждом из которых радиальная компонента направ­лена либо наружу, либо вовнутрь.

В пределах каждого сектора скорость солнечного ветра и плотность частиц систематически изменяются. Наблю­дения с помощью ракет показывают, что оба параметра резко увеличиваются на границе сектора. В конце второго дня после прохождения границы сектора плотность очень быстро, а затем, через два или три дня, медленно начинает расти. Скорость солнечного ветра уменьшается медленно на второй или третий день после достижения пика. Сек­торная структура и отмеченные вариации скорости и плот­ности тесно связаны с магнитосферными возмущениями. Секторная структура довольно устойчива, поэтому вся структура потока вращается с Солнцем по крайней мере в течение нескольких солнечных оборотов, проходя над Землей приблизительно через каждые 27 дней.

Магнитное поле земли

Английский ученый Уильям Гильберт, придворный врач королевы Елизаветы, в 1600 г. впервые показал, что Земля является магнитом, ось которого не совпадает с осью вращения Земли. Следовательно, вокруг Земли, как и около любого магнита, существует магнитное поле. В 1635 г. Геллибранд обнаружил, что поле земного маг­нита медленно меняется, а Эдмунд Галлей провел первую в мире магнитную съемку океанов и создал первые миро­вые магнитные карты (1702 г.). В 1835 г. Гаусс провел сферический гармонический анализ магнитного поля Земли. Он создал первую в мире магнитную обсерваторию в Гёттингене.

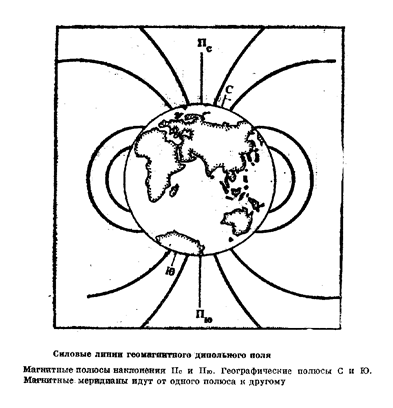О распределении силовых линий магнитного дипольного поля и о магнитных полюсах наклонения П_с , П_ю можно судить по рисунку.

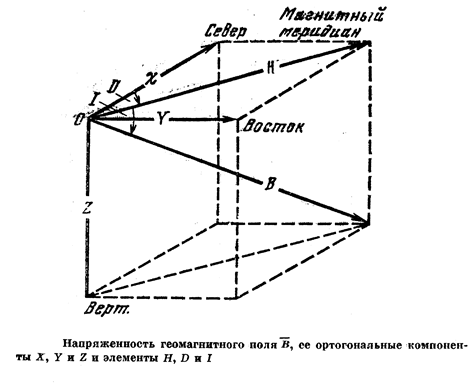
Составляющие геомагнитного поля определены следую­щим образом. В любой точке О вектор напряженности магнитного поля В может быть разложен на составляющие, как это показано на рисунке. Можно выбрать в качестве составляющих абсолютную величину полного вектора В (модуль) и два угла: D и I . Угол D образован направле­нием на север и горизонтальной составляющей вектора В , т. е. Н ; I – это угол между В и Н , Угол D считается по­ложительным, если Н отклоняется к востоку, а I положи­тельно при отклонении В вниз от горизонтальной плоско­сти. Величина D называется магнитным склонением, а I – ­наклонением. Вертикальная плоскость, которая проходит через Н, именуется местной магнитной меридиональной плоскостью.

Используется также разложение В на северную (X) и восточную (Y) составляющие вектора Н. Третьей служит вертикальная составляющая Z, которая считается положительной, если В направлено вниз. Напряженности B, H, Z, X, Y измеряются в гауссах (Гс) или гаммах (g). 1g=10^{- 5} Гс. Углы D и I измеряются в дуговых градусах и минутах. Все приведенные семь величин В, Н, D, I, X, У, Z называются магнитными элементами. Соотношения между ними ясны из рисунка.

H=B cos I, Z=B sin I=H tg I,

X=H cos D, Y=H sin D,

X² +Y² =H² X² +Y² +Z² =H² +Z² =B²

Ясно, что для полного описания вектора В достаточно иметь три независимых элемента. По ним могут быть рас­считаны все остальные.

Обычная стрелка магнитного компаса уравновешивает­ся, вращаясь горизонтально на вертикальной оси. В север­ной полусфере Земли почти везде северный полюс магнитной стрелки направлен вниз (т. е. I положительно), а в южном полушарии I отрицательно, поскольку вниз направлен южный полюс стрелки. Линия, которая разде­ляет области положительного и отрицательного I, назы­вается магнитным экватором или экватором наклонения. Естественно, что на ней I=0, т. е. магнитная стрелка в лю­бой точке на этой кривой располагается горизонтально.

На полюсах магнитного наклонения горизонтальная компонента полного вектора В исчезает и магнитная стрел­ка устанавливается вертикально. Эти точки еще называют полюсами наклонения. Таких точек в принципе может быть несколько. Две основные из них обычно называются магнитными полюсами Земли. Они расположены в Арк­тике и в Антарктиде. Координаты их 75°,6 с. ш., 101° з. д. и 66°,3 ю.ш., 141° в. д. Местоположение магнитных по­люсов не является постоянным. Приведенные выше коор­динаты относятся к эпохе 1965 г.

Чтобы определить азимут[3] вектора Н , нужно выбрать некоторое нулевое направление, от которого можно отсчи­тывать магнитное склонение D. За такое направление при­нято направление на северный географический полюс. Та­ким образом, D определяется относительно условного на­правления, поскольку ось вращения Земли не связана не­посредственно с конфигурацией геомагнитного поля. То же относится и к элементам Х и Y. Поэтому D, X, Y назы­вают относительными магнитными элементами, тогда как H, Z и I именуются собственными магнитными эле­ментами.

Несколько слов о магнитных картах. Обычно через каждые 5 лет распределение магнитного поля на поверх­ности Земли представляется магнитными картами трех или более магнитных элементов. На каждой из таких карт проводятся изолинии, вдоль которых данный элемент имеет постоянную величину. Линии равного склонения D назы­ваются изогонами, наклонения I – изоклинами, величины полной силы В – изодинамическими линиями или изодинами. Изомагнитные линии элементов H, Z, Х и Y назы­ваются соответственно изолиниями горизонтальной, вер­тикальной, северной или восточной компонент.

Направление оси магнитного диполя практически не меняется с 1829 г. При этом магнитный момент диполя систематически уменьшался. Его уменьшение может быть аппроксимировано выражением

m=(15,77-0,003951t)10²⁵ Гссм³ ,

где t — время в годах, отсчитываемое вперед пли назад от 1900 г. н. э. По этой формуле можно рассчитать, что если уменьшение магнитного момента будет продолжаться с та­кой же скоростью, то к 3991 г. магнитный момент станет равным нулю.

Мы будем постоянно иметь дело с геомагнитными си­ловыми линиями, а также различного рода координатами.

Геомагнитные дипольные координаты — это дополнение к широте q’ и восточной долготе j. Они определяются относительно полярной оси и нулевого меридиана. Если точка Р имеет географические координаты q и j, то гео­магнитные координаты могут быть вычислены по следую­щим формулам:

cosq’=-cosq cosq₀ - sinq sinq₀ cos(j-j₀ ),

sinj’=sinq sin(j-j₀ ) cosecq’.

Магнитное склонение дипольного поля Y – это угол, обра­зованный магнитным и географическим меридианами в точке Р. Он определяется из выражения

sin(–y)= sinq₀ (sin(j-j₀ )/sinq’)

Существуют таблицы, которые содержат геомагнитные координаты сетки точек, расположенных через ровные угловые интервалы в географических координатах q и j. Имеются также сетки географических и геомагнитных координат. По этим сеткам можно легко найти геомагнит­ные координаты любой точки с известными географически­ми координатами, и наоборот.

Обратный переход от геомагнитных координат к геогра­фическим можно произвести по формулам

cosq=cosq’ cosq₀ – sinq’ sinq₀ cosj’

Если рассматривать только дипольную часть геомагнит­ного поля в любой точке Р с геомагнитными координатами q’ и j, то потенциал V₁ , описываемый членами первого порядка, равен V₁ = –m(cosq/r² ) Tак как V₁ не зависит от долготы, то восточная компонента дипольного поля В рав­на нулю. Северная Я и вертикальная Z составляющие поля получаются равными

H=m(sinq’/r³ )=H₀ (a/r)³ sinq’,

Z=2m(cosq’/r³ )=Z₀ (a/r)³ cosq’; Z₀ =2H₀

где Z₀ и Н₀ – максимальные значения Z и H на геоцентри­ческой сфере радиуса а , содержащей точку Р. H₀ соответ­ствует полю на геомагнитном экваторе, а Z₀ – на северном полюсе. На южном полюсе Z= –Z₀ .

Наклонение I и магнитную широту l можно опреде­лить из следующих уравнений:

tgI=(Z/H)2ctgq’, tgl=1/2tgI.

Каждая силовая линия дипольного поля лежит в плоскости геомагнитного меридиана. Ее уравнение

r=r_e sin² q’

где r_e – радиальное расстояние, на котором данная сило­вая линия пересекает плоскость геомагнитного экватора, с величиной поля равной m/r_e ³ Величину r_e , можно принять за параметр, определяющий силовую линию.

Напряженность поля в точке Р можно определить через параметр силовой линии

B=H² +Z² =mc/r³ =m/r_e ³ c/sin6q’=B_e c/sin6q’,

B_c =m/r_e ³

Представление геомагнитного поля центральным ди­полем только лишь первое весьма грубое приближение. Используя более высокие члены разложения по сфериче­ским гармоникам, можно построить геомагнитную систему координат, лучшую, чем дипольная. Так, если использовать наряду с дипольными еще пять старших сферических гар­монических членов и рассчитать геометрическое место то­чек пересечения земной поверхности садовыми линиями, которые располагаются в экваториальной плоскости на расстоянии пяти-шести радиусов Земли, то полученная таким образом линия хорошо совпадает с зоной полярных сияний.

Было также показано, что если проектировать по силовым линиям на поверхность Земли лежащие в плоско­сти экватора геоцентрические окружности с радиусами L_c =a cosec² q_c , то полученные таким путем широты q_c упорядочивают явления в полярной шапке лучше, чем дипольные геомагнитные широты.

Часто используют «исправленные» геомагнитные коор­динаты при описании различных авроральных явлений и поглощения космического радиоизлучения в полярной шап­ке. Они были рассчитаны Хакурой на основе исследований Халтквиста. Дальнейшее усовершенствование этих «ис­правленных» геомагнитных координат выполнил Густавсон, использовав коэффициенты разложения поля на эпоху 1965 г.

При объяснении некоторых явлений, которые связаны с суточными вариациями полярных сияний, было введено понятие геомагнитных полуночи и полудня. Затем появи­лось и более общее понятие геомагнитного времени.

Если данная точка определена географическими коор­динатами q и j и геомагнитными координатами q и j, то геомагнитное время может быть выражено соотноше­нием 15°t’=j’_H – j’. Здесь j’_H – геомагнитная долгота полу­дня в данный момент времени. Геомагнитное время t от­считывается от геомагнитного полудня и относительно истинного положения Солнца Н .

Используя схему определения «геомагнитного времени» в системе геомагнитных координат, приведем пример его расчета. Если в Гринвиче истинное время t_G , в точ­ке Р местное истинное время составит t_G +j/15°, то геогра­фическая долгота истинного положения Солнца будет 180° – 15° t_G . Отсюда, учитывая также полярный угол этого положения (который определяется как 90°– d, где d обо­значает склонение Солнца), геомагнитную долготу j’_H мож­но рассчитать по приведенным выше формулам. Гринвич­ское среднее время в этот момент будет t_G – e, где е обозна­чает «уравнение времени».

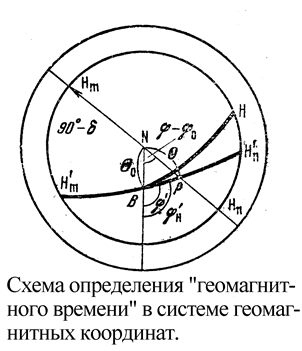Вернемся к рисунку. Там показан круг с угловым радиу­сом 90°– d, который описывает положение Солнца на зем­ной поверхности. Дуга большого круга, проведенная через точку Р и геомагнитный полюс В, пересекает этот круг в точках H’_n и H’_m , которые указывают положение Солнца соответственно в моменты гео­магнитного полудня и геомаг­нитной полуночи точки Р. Эти моменты зависят от широты точки Р. Положения Солнца в местные истинные полдень и полночь указаны точками H_n и Н_m соответственно. Когда d по­ложительно (лето в северном полушарии), то утренняя поло­вина геомагнитных суток не равна вечерней. В высоких ши­ротах геомагнитное время мо­жет очень сильно отличаться от истинного или среднего вре­мени в течение большей части суток.

Говоря о времени и систе­мах координат, скажем еще об учете эксцентричности магнитного диполя. Эксцентрич­ный диполь медленно дрейфует наружу ( к северу и к западу) с 1836 г. Экваториальную плоскость он пересел? примерно в 1862 г. Его траектория по радиальной проек­ции расположена в районе о-ва Гилберта в Тихом океане.

Ось эксцентрического диполя, проведенная через точ­ку О параллельно АВ, пересекает поверхность Земли в точках В и A, которые расположены соответственно вблизи В и А. В этих точках наклонение поля эксцентри­ческого диполя не равно нулю. Полоса наклонения поля эксцентрического диполя (точки В и А) находится в ме­ридиональной плоскости ВОА несколько дальше от точек В и А. Западная долгота этой плоскости в геомагнитной системе координат возросла с 110° в 1836 г. до 143° в 1965 г. Углы ВОВ и АОА за этот же промежуток времени увеличились с 2,4° до 40°. Углы ВОВ и АОА, как правило, не равны друг другу: в 1836 г. они составля­ли 7,2° и 5,5°, а в 1965 г.- 11,8° та. 13,2°.

Геомагнитные индексы. Геомагнитная активность опи­сывается различными геомагнитными индексами, исполь­зуемыми в геомагнетизме, физике ионосферы, солнечной физике, физике полярных сияний. Магнитные обсервато­рии всего мира посылают свои индексы в Международный центр Де Бильт (Нидерланды), который связан с Постоян­ной Службой геомагнитных индексов в Гёттингене (ФРГ). Эти локальные индексы — основа планетарных индексов. Остановимся на них подробнее.

Индексы С и С _i . Магнитограмма на каждой обсерва­тории за каждые сутки (начало суток отсчитывается от 00 ч гринвичского времени) оценивается по степени возмущенности магнитного поля баллами 0, 1 или 2. Баллы выбираются простым просмотром магнитограмм. Это и есть индекс С для данных суток данной обсерватории. Затем индексы С поступают в единый центр и там усредняются с точностью до 0,1 для каждых суток. Так определяется значение международного ежедневного индекса С_i . Индек­сы C_i имеют градации через 0,1, в результате чего полу­чается 21-балльная классификация гринвичских суток (от 0,0 для спокойных дней до 2,0 для возмущенных).

Чаще всего в анализах используются индексы k и k_р . Эти индексы определяются для 3-часовых интервалов, т. е. имеется восемь значений индексов для каждых грин­вичских суток. При определении k-индексов берутся три компоненты магнитного поля: Н, D и Z. Для каждой ком­поненты оценивается амплитуда r в течение 3-часового интервала. Наибольшая из трех амплитуд в каждом вре­менном интервале употребляется для вывода k-индекса. Составлены таблицы, дающие пределы r, определяемые полулогарифмической шкалой, для каждой обсерватории и для каждой из 10 величин k (0,1,... 9). Эта связь меж­ду r и k выбирается такой, чтобы весь диапазон измене­ния геомагнитной активности, от самых спокойных усло­вий до самой мощной бури, можно было выразить в шкале, состоящей из одной цифры. Нижний предел r для k=9 в зависимости от общего уровня геомагнитной активности является большим или меньшим. В зоне полярных сияний этот предел равен 2500g, тогда как для обсерваторий низ­ких широт 300g. Так определяется местный (локальный) индекс k.

Планетарный индекс k или k_p – индекс Бартельса слу­жат для выражения характеристики планетарной геомаг­нитной активности. Исправленные и стандартизованные значения k подготавливаются Постоянной службой в Гёт­тингене для каждой из 12 выбранных обсерваторий, рас­положенных в северном и южном полушариях. Среднее значение k-величин этих 12 обсерваторий и дает величину k_p -индекса. Он называется планетарным трехчасовым ин­дексом и выражается в шкале с точностью до ¹ /₃ :

0₀ , 0₊ , 1_– , 1_о , 1₊ , 2_- , 2_о , 2₊ , 3_- , 3_о , 3₊ ...... 9_- , 9_о , 9₊ .

Всего получится 28 баллов.

Ежедневный индекс Sk_р получается суммированием величин за 8 3-х часовых интервалов суток.

k_р -индекс обладает полулогарифмической связью с ам­плитудой r. Если перевести k_p в линейную шкалу, то по­лучится а_р -индекс. Имеется таблица для пересчета индек­сов k_p в индексы а_p . Сумма восьми величин а_p для каж­дого дня дает ежедневный A_р -индекс.

На основании индексов А_р можно рассчитать индек­сы С_р , которые имеют величины от 0,0 до 2,0 через 0,1 (всего 21 величины). Имеется таблица пересчета А_р в С_р .

На основании индекса С_р рассчитывается индекс С_g (всего 10 величин: 0,1,... 9). Значения С_р разбиты на диапазоны, каждый из которых соответствует определен­ной величине С₉ (0,0-0,1; 0,2-0,3; 0,4-0,5; 0,6-0,7; 0,8-0,9; 1,0-1,1; 1,2-1,4; 1,5-1,8; 1,9; 2,0-2,5).

Описанные индексы геомагнитного поля либо не учиты­вают, либо недостаточно учитывают структуру составляю­щих магнитного поля и его частей. Поэтому они обычно не используются для детальных количественных исследова­ний. Существуют и другие, более детальные индексы.

D_st -индекс дает среднее по долготе уменьшение гори­зонтальной составляющей поля на низких широтах в еди­ницах g, которое пропорционально полной кинетической энергии инжектированных частиц, захваченных в радиа­ционном поясе. D_st -индекс выражает амплитуду первого коэффициента гармонического ряда, который получается при Фурье-разложении поля главной фазы магнитной бури как функции геомагнитной долготы.

Индексы АЕ, AL и AU разработаны для получения интенсивности авроральной электроструи в g. Они позво­ляют контролировать интенсивность полярной электро­струи по вариациям горизонтальной компоненты магнитного поля на обсерваториях зоны полярных сияний и рав­номерно расположенных по долготе. АE-индекс получается суперпозицией этих записей. Когда произведена супер­позиция записей магнитного поля, то расстояние между верхней и нижней кривыми и есть AE-индекс. Верхняя огибающая дает АU-индекс, а нижняя огибающая – AL-индекс. Эти индексы можно получить в неограниченном разрешении во времени. Но обычно достаточно иметь их значение через 2,5 мин.

[1] Солнечный ветер – истечение плазмы солнечной короны в межпланетное пространство. На уровне орбиты Земли средняя скорость частиц Солнечного ветра (протонов и электронов) около 400 км/с, число частиц – несколько десятков в 1см³ .

[2] Астрономическая единица длины – единица расстояний в астрономии, равная среднему расстоянию Земли от Солнца (1а. е.=149,6 млн. км).

[3] Азимут – угол (А) между плоскостью меридиана точки наблюдения и вертикальной плоскостью, проходящей через эту точку и наблюдаемый объект. Азимут – одна из координат системы горизонтальных координат в астрономии.

Скачать архив с текстом документа