Математический анализ
СОДЕРЖАНИЕ: Исследование заданной функции и построение ее графика. Расчет объема тела, полученного вращением вокруг оси абсцисс фигуры, ограниченной линиями и осями координат. Вычисление интеграла при заданной силе. Работа, которую нужно совершить для сжатия пружины.Оглавление
Задание 1.
Исследовать функцию и построить ее график: 
.
Решение:
y = 0, если х = 0 или х = 
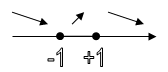
y(-1) = -2, y(1) = 2.
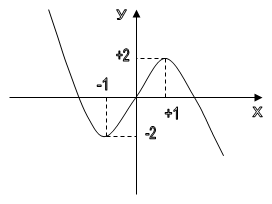
Задание 2
1. 
;
2. 
;
3. 
;
4. 
;
5. Найти dy, если 
.
Решение:
1. 
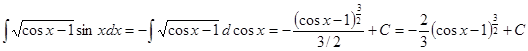
2. 
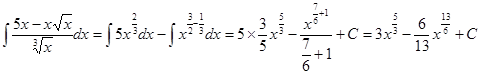
3. 
4. 
5. 
, 
Ответ: 1. 
; 2. 
; 3. 
; 4. 
; 5. 
.
Задание 3.
Вычислить объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной линиями 
, х = 3 и осями координат.
Решение:
.
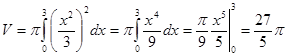Ответ:
.
Задание 4.
Для сжатия пружины на L см требуется сила 9,8 Н. Какую работу надо совершить, чтобы сжать пружину на 0,05 м.
Решение:
Работа 
, где F – сила, s – расстояние, пройденное под действием этой силы.
По закону Гука 
, где 
- абсолютное удлинение стержня, F – сила упругости, k – жесткость материала. Следовательно,
.
Ответ: 
.
Задание 5.
Найти интеграл:
а)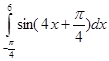 
;б) 
.
Решение:
а) 
б) 
.
Ответ: а) 
; б) 
.
Задание 6.
Исследовать функцию и построить ее график:
1. 
;
2. 
;
3. 
;
4. 
;
5. 
Решение:
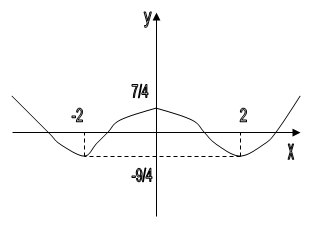
1. - симметрична относительно оси Ох
y = 0, если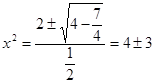 
, т.е. 
.
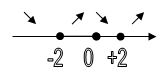
y(-2) = y(2) = -9/4
y(0) = 7/4
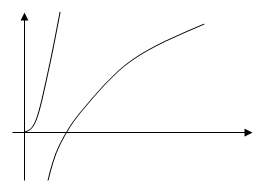
2.
Область определения 
y = 0, если 
, корней нет:
, если 
Корень один, он близок к х = 1, находится между х = 1,05 и х = 1,06, это точка минимума.
y(1) = 2, y(2) = 3.2, y(3) = 4,95
3.
y = 0, если х = 1,
область определения 
,
, х = 0 – асимптота.
;
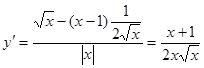корней, принадлежащих области определения, нет.
;
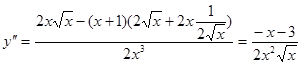корней, принадлежащих области определения, нет.
4.
Уравнение y = 0 корней не имеет,
, 
, х = 1/5 – асимптота
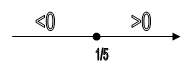
y(0.007) = -0.3
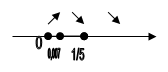
5.
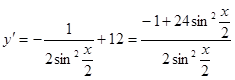
y(0.4 + 4k) = 4.9 + 48k
y(-0.4 + 4k) = -4.9 + 48k
,
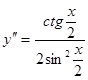знак совпадает со знаком ctg(x/2)
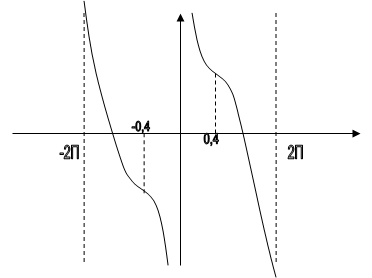
Литература
1. Зорич В.А. Математический анализ. Ч. 1, М., 2001. Ч. 2. 2001.
2. Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч. 1. М., 2001. Ч. 2, М., 2002.
3. Кудрявцев Л.Д. Курс математического анализа: В 3 т. М., 1988-1989.
4. Камынин Л.И. Курс математического анализа. Т. 1. М., 1993. Т. 2. М., 1995.
5. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М., 2003.