Математична статистика
СОДЕРЖАНИЕ: Методи рішення задач математичної статистики, яка вивчає статистичні закономірності методами теорії ймовірностей за статистичними даними - результатами спостережень, опитувань або наукових експериментів. Способи збирання та групування статистичних даних.Математична статистика
(реферат)
1. Задачі математичної статистики
Математична статистика як наука вивчає статистичні закономірності методами теорії ймовірностей за статистичними даними - результатами спостережень, опитувань або наукових експериментів.
Математична статистика розв’язує дві основні задачі.
Перша задача математичної статистики – вказати способи збирання та групування статистичних даних.
Друга задача математичної статистики – розробити методи аналізу статистичних даних у залежності від мети дослідження. Сюди відносяться:
а) оцінка невідомої ймовірності; оцінка невідомої функції розподілу; оцінка параметрів розподілу, вигляд якого відомий; оцінка залежності випадкової величини від однієї або декількох випадкових величин та інші;
б) перевірка статистичних гіпотез про вигляд невідомого розподілу або про величину параметрів розподілу, якщо він відомий.
Сучасна математична статистика розробляє способи визначення кількості експериментів до початку дослідження (планування експерименту ), під час експерименту (послідовний аналіз ) і розв’язує багато інших задач.
Отже, математична статистика вивчає методи збирання та обробки статистичних даних для одержання наукових та практичних висновків.
2. Генеральна та вибіркові сукупності
Нехай необхідно вивчити сукупність однорідних об’єктів відносно деякої ознаки (кількісної або якісної). Іноді для цього проводять суцільне обстеження, при якому досліджується кожний об’єкт сукупності. На практиці суцільне обстеження використовується порівняно рідко. Є декілька причин для цього:
· сукупність має велику кількість об’єктів, яку обстежити фізично неможливо;
· обстеження об’єкта вимагає його фізичного знищення;
· для обстеження одного об’єкту необхідні значні матеріальні витрати.
В таких випадках вибирають із всієї сукупності об’єктів порівняно невелику кількість об’єктів, яку називають вибіркою , і обстежують їх. Множина об’єктів, з якої здійснюється вибірка називається генеральною сукупністю . Число елементів вибірки називають об’ємом вибірки , ачисло елементів генеральної сукупності – об’ємом генеральної сукупності . Генеральна сукупність може мати скінченну або нескінченну кількість елементів.
Приклад 2.1.Множина деталей виготовлена у цеху є скінченною генеральною сукупністю.
Приклад 2.2. Множина можливих значень, які можна отримати у результаті вимірювання фізичної величини є нескінченною генеральною сукупністю.
Часто генеральна сукупність має скінченну кількість об’єктів. Але якщо це число достатньо велике, то можна вважати, що генеральна сукупність має нескінченну кількість об’єктів. Це значно спрощує розрахунки без суттєвої втрати точності результатів. Таке спрощення виправдовується тим, що збільшення об’єму генеральної сукупності практично не впливає на результати обробки статистичних даних.
При здійсненні вибірки можна поступати способами: після того, як об’єкт вибраний і над ним виконано спостереження, його або повертають або не повертають у генеральну сукупність. У відповідності до цього розрізняють повторні вибірки , коли вибрані об’єкти повертаються в генеральну сукупність, і безповторні – коли не повертаються.
Для того, щоб за даними вибірки можна було б зробити вірні висновки про генеральну сукупність, необхідно щоб вибірка правильно представляла пропорції генеральної сукупності. Цю умову коротко формулюють так: вибірка повинна бути репрезентативною .
На підставі закону великих чисел можна стверджувати, що вибірка буде репрезентативною, якщо її здійснити випадково. Кожний об’єкт вибірки вибраний випадково із генеральної сукупності, якщо всі об’єкти мають однакову ймовірність попасти у вибірку.
Якщо об’єм генеральної сукупності достатньо великий, а вибірка складає незначну її частину, то різниця між повторною і безповторною вибірками незначна; у граничному випадку, коли генеральна сукупність нескінченна, а вибірка скінченна, різниця між вибірками зникає зовсім.
На практиці використовуються різні способи відбору об’єктів у вибірку. Принципово ці способи можна розділити на два види:
1) відбір, що не вимагає розбиття генеральної сукупності на частини. Сюди належать: а) простий випадковий безповторний відбір; б) простий випадковий повторний відбір.
2) відбір, при якому генеральна сукупність розбивається на частини. Сюди належать: а) типовий відбір; б) механічний відбір; в) серійний відбір.
Простим випадковим називають відбір, при якому об’єкти вибираються по одному із всієї генеральної сукупності. Якщо при цьому об’єкти повертаються у генеральну сукупність, то відбір є простим випадковим повторним, якщо ні – простим випадковим безповторним.
Типовим називають відбір, при якому об’єкти вибираються не з усієї генеральної сукупності, а з кожної її “типової” частини.
Приклад 2.3. Якщо деталі виготовляються на декількох станках, то деталі випадковим чином вибирають із деталей виготовленних на кожному окремому станку.
Механічним називають відбір, при якому генеральна сукупність випадковим чином розбивається на частини і з кожної частини випадково вибирають один об’єкт. Кількість таких частин має дорівнювати необхідному об’єму вибірки.
Приклад 2.4. Якщо необхідно вибрати 20% деталей, то вибирають кожну п’яту; якщо необхідно вибрати 5% деталей, то відбирають кожну двадцяту.
Суттєвим недоліком механічного відбору є те, що він не завжди забезпечує репрезентативність вибірки.
Приклад 2. Якщо відбирають кожний двадцятий валик, причому одразу після цього міняють різак, то відібраними виявляться валики, обточені затупленним різаком.
Серійним називають відбір, при якому об’єкти вибираються з генеральної сукупності не по одному, а серіями, які піддаються суцільному обстеженню.
Приклад 2.6. Якщо вироби виготовляються великою кількістю станків, то здійснюють суцільне обстеження продукцію лише декількох випадково вибраних станків.
Серійним відбором користуються коли ознака, відносно якої обстежується генеральна сукупність мало коливається в різних серіях об’єктів.
На практиці часто використовуються комбінований відбір, при якому сполучають вказані вище способи.
3. Статистичні розподіли та чисельні характеристики вибірки
Значення чисельної ознаки, які спостерігаються в деякій конкретній вибірці, називають варіантами
. Послідовність таких варіант у зростаючому порядку – варіаційним рядом
. Якщо у вибірці об’єму n
варіанта ![]() зустрічається
зустрічається ![]() разів, то число
разів, то число
![]() (3.1)
(3.1)
називають відносною частотою варіанти
, а ![]() – частотою варіанти
.
– частотою варіанти
.
Від вибірки до вибірки об’єму n
частоти![]() та відносні частоти
та відносні частоти ![]() змінюються. Це означає, вони є значеннями випадкових величин
змінюються. Це означає, вони є значеннями випадкових величин ![]() та
та ![]() , відповідно. В подальшому все що стосується конкретної вибірки буде позначатися малими буквами латинського та грецького алфавітів, а все що стосується вибірки взагалі – відповідними великими буквами.
, відповідно. В подальшому все що стосується конкретної вибірки буде позначатися малими буквами латинського та грецького алфавітів, а все що стосується вибірки взагалі – відповідними великими буквами.
Перелік варіант та відповідних до них частот (або відносних частот) називають статистичним розподілом вибірки . Статистичний розподіл, як правило, задається у вигляді таблиці. Ломана крива, яка з’єднує точки з координатами (xi , ni ), або (xi , wi ) у прямокутній системі координат називається полігоном частот .
Приклад 3.1. Для конкретної вибірки одержали статистичний розподіл відносних частот
![]() .
.
Його гістограма має вигляд
Статистичний розподіл вибірки можна також представити у вигляді послідовності інтервалів та відповідних до них частот, що особливо зручно, коли ознакою є неперервна величина. Інтервал з варіантами розбивають на декілька часткових інтервалів довжиною 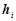 і знаходять для кожного з них суму частот варіант, які потрапили в інтервал. Якщо всі інтервали рівні (
і знаходять для кожного з них суму частот варіант, які потрапили в інтервал. Якщо всі інтервали рівні (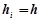 ), то відповідні варіанти називають рівновіддаленими, а їх чисельні значення визначаються серединами відрізків. Якщо частота первинної варіанти знаходиться на границі двох інтервалів, то її частота рівномірно розподіляється між ними. Графічно статистичний розподіл з послідовністю інтервалів задається гістограмою частот (відноснихчастот). Для побудови гістограми частот (або відносних частот), необхідно на вісі абсцис відкласти часткові інтервали і побудувати на них як основах прямокутники висотою
), то відповідні варіанти називають рівновіддаленими, а їх чисельні значення визначаються серединами відрізків. Якщо частота первинної варіанти знаходиться на границі двох інтервалів, то її частота рівномірно розподіляється між ними. Графічно статистичний розподіл з послідовністю інтервалів задається гістограмою частот (відноснихчастот). Для побудови гістограми частот (або відносних частот), необхідно на вісі абсцис відкласти часткові інтервали і побудувати на них як основах прямокутники висотою 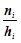
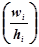 . Величини
. Величини 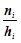 називають густиноючастоти, а величини
називають густиноючастоти, а величини 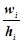 - густиною відносної частоти. Загальна площа гістограми дорівнює сумі всіх частот, тобто об’єму вибірки n, а площа гістограми відносних частот дорівнює одиниці.
- густиною відносної частоти. Загальна площа гістограми дорівнює сумі всіх частот, тобто об’єму вибірки n, а площа гістограми відносних частот дорівнює одиниці.
Приклад 3.2. Для конкретної вибірки обєму ![]() одержали розподіл частот по частковим інтервалам
одержали розподіл частот по частковим інтервалам
Частковий інтервал довжиною
|
Сума частот варіант часткового інтервалу |
Густина частоти |
5-10 10-15 15-20 20-25 25-30 30-35 35-40 |
4 6 16 36 24 10 4 |
0.8 1.2 3.2 7.2 4.8 2.0 0.8 |
Полігон частот такого розподілу має такий вигляд
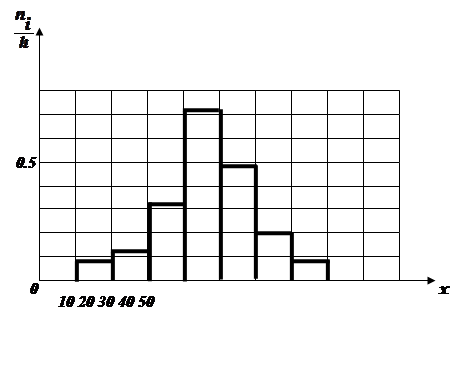
Емпіричною інтегральною функцією вибіркиназивають функцію
![]() ,(3.2)
,(3.2)
![]() –
кількість варіант менших ніж x
(дискретна випадкова аеличина).
–
кількість варіант менших ніж x
(дискретна випадкова аеличина).
На відміну від емпіричної інтегральної функції розподілу вибірки, інтегральну функцію розподілу генеральної сукупності називають теоретичною інтегральною функцією розподілу.
З теореми Бернуллі слідує, що відносна частота події ![]() тобто
тобто ![]() по ймовірності прямуєдо ймовірності
по ймовірності прямуєдо ймовірності ![]() цієї події. Це означає, що емпірична функція вибірки по ймовірності прямує до теоретичної функції розподілу генеральної сукупності. Тому емпірична функція розподілу вибірки є оцінкою
теоретичної функції генеральної сукупності.
цієї події. Це означає, що емпірична функція вибірки по ймовірності прямує до теоретичної функції розподілу генеральної сукупності. Тому емпірична функція розподілу вибірки є оцінкою
теоретичної функції генеральної сукупності.
Із означення емпіричної функції слідують такі її властивості:
1. значення емпіричної функції належать відрізку [0; 1] ;
2. ![]() – неспадна функція;
– неспадна функція;
3. якщо![]() – найменша варіанта, то
– найменша варіанта, то ![]() при
при ![]() ; якщо
; якщо ![]() – найбільша варіанта, то
– найбільша варіанта, то
4. ![]() при
при ![]() .
.
Статистичні розподіли конкретної вибірки характеризуються початковими
![]() (3.3)
(3.3)
та центральними
![]() (3.4)
(3.4)
емпіричними моментами степені k .
Від вибірки до вибірки емпіричні моменти змінюються і тому мають розглядатися як значення випадкових величин
![]()
![]() ,
,
відповідно (![]() - великі букви грецького алфавіту, відповідні до них малі букви
- великі букви грецького алфавіту, відповідні до них малі букви ![]() ).
).
Початкові та центральні емпіричні моменти визначаються аналогічним чином, як і моменти дискретних випадкових величин, лише замість ймовірностей використовуються відносні частоти. Тому всі терміни та співвідношення між моментами випадкової величини справедливі і для емпіричних моментів вибірки (необхідно лише замість теоретичних моментів підставити відповідні емпіричні). При великій кількості спостережень емпіричні моменти прямують по ймовірності до відповідних теоретичних моментів.
При обчисленнях емпіричних моментів зручно використовувати умовні варіанти
![]() ,
(3.5)
,
(3.5)
c – стала величина (умовний нуль) . Якщо варіаційний ряд складається з рівновіддалених варіант з кроком h і в якості умовного нуля вибрана одна з варіант, то умовні варіантами виражаються цілими числами.
Спочатку обчислюються початкові моменти для умовних варіант, які називаються умовними емпіричними моментами:
![]()
![]() ,(3.6)
,(3.6)
а потому і самі емпіричні моменти:
![]() ,(3.7)
,(3.7)
![]() (3.8)
(3.8)
![]() (3.9)
(3.9)
![]() (3.10)
(3.10)
Доведення.
![]() ,
,
звідки ![]() .
.
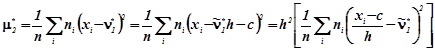
![]()
![]()
![]() .
.
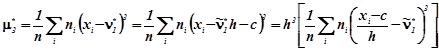
![]()
![]()
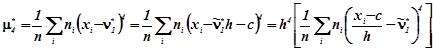
![]()
![]()
Приклад 3.3.
Для вибірки об’єму ![]() одержані такі результати:
одержані такі результати:
1.00 1.03 1.05 1.06 1.08 1.10 1.12 1.15 1.16 |
1 3 6 4 2 4 3 6 5 |
1.19 1.20 1.23 1.25 1.26 1.29 1.30 1.32 1.33 |
2 4 4 8 4 4 6 4 5 |
1.37 1.38 1.39 1.40 1.44 1.45 1.46 1.49 1.50 |
6 2 1 2 3 3 2 4 2 |
Необхідно обчислити початковий момент першого порядку та другий, третій, четвертий центральний моменти вибірки.
Розв’язування
. Об’єм вибірки достатньо великий і тому має зміст перейти до статистичного розподілу для рівновіддалених варіант. Для цього область значень розбивається на однакові інтервали ![]() з кроком
з кроком ![]() і підраховується сума частот для кожного відрізку. За рівновіддалені частоти доцільно взяти середини інтервалів. У результаті одержується такий розподіл:
і підраховується сума частот для кожного відрізку. За рівновіддалені частоти доцільно взяти середини інтервалів. У результаті одержується такий розподіл:
![]() .
.
Для подальших обчислень зручно вибрати в якості умовного нуля варіанту 1.25
: ![]() . У такому випадку розподіл умовних варіант (3.5) такий:
. У такому випадку розподіл умовних варіант (3.5) такий:
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Умовні початкові моменти обчислюються за формулами (3.6):
![]() ;
; ![]() ;
;![]() ;
;![]() ;
;
На підставі формул (3.7 – 3.10) при ![]() :
:
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]()
![]() .
.
4. Стандартні розподіли математичної статистики
4.1 Розподіл ![]() (хі-квадрат
)
(хі-квадрат
)
Нехай ![]() - система нормальних випадкових величин з одинаковими математичними сподіваннями
- система нормальних випадкових величин з одинаковими математичними сподіваннями ![]() та середньоквадратичними відхиленнями
та середньоквадратичними відхиленнями ![]() . Тоді сума квадратів цих величин
. Тоді сума квадратів цих величин ![]() розподілена за законом
розподілена за законом ![]() (хі квадрат) із
(хі квадрат) із ![]() степенями свободи. Густина розподілу
степенями свободи. Густина розподілу ![]()
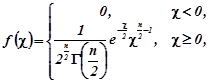 (4.1.1)
(4.1.1)
де ![]() - гамма-функція (додаток 1.11).
- гамма-функція (додаток 1.11).
Розподіл ![]() однозначно визначається одним параметром – числом степені свободи n
. Із збільшенням числа степеней свободи розподіл повільно наближається до нормального (додаток 1.12).
однозначно визначається одним параметром – числом степені свободи n
. Із збільшенням числа степеней свободи розподіл повільно наближається до нормального (додаток 1.12).
Математичне сподівання та дисперсія розподілу ![]()
![]() ,
,
![]() .
.
Доведення . За означенням математичного сподівання
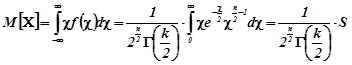 ,
,
![]()
![]() ,
,
(використана рівність ![]() ).
).
З врахуванням цього
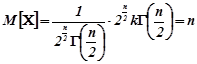 .
.
Для обчислення дисперсії зручно скористатися формулою
![]() .
.
За означенням математичного сподівання
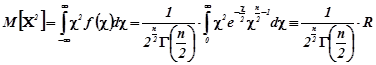 ,
,
![]()
![]()
![]()
З врахуванням цього
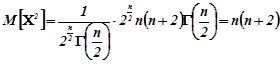
![]() .
.
4.2 Розподіл Стьюдента
Якщо Z
– нормальна випадкова величина з параметрами ![]() та
та ![]() , а V
– незалежна від Z
величина, розподілена за законом
, а V
– незалежна від Z
величина, розподілена за законом ![]() із n
степенями свободи, то випадкова величина
із n
степенями свободи, то випадкова величина
![]()
має розподіл, який називають розподілом Стьюдента , з густиною
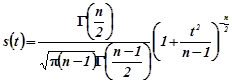 .(4.2.1)
.(4.2.1)
Розподіл Стьюдента однозначно визначається одним параметром – числом степеней свободи розподілу випадкової величини V (додаток 1.13)
Функція ![]() симетрична, тому математичне сподівання розподілу Стьюдента дорівнює нулю:
симетрична, тому математичне сподівання розподілу Стьюдента дорівнює нулю:
![]() ,(4.2.2)
,(4.2.2)
а дисперсія
![]() .(4.2.3)
.(4.2.3)
4.3 Розподіл F Фішера-Снедекора
Якщо U
іV
– незалежні випадкові величини розподілені за законом ![]() з
з ![]() степенями свободи, відповідно, то випадкова величина
степенями свободи, відповідно, то випадкова величина
![]() (4.3.1)
(4.3.1)
має розподіл , який називається розподілом F Фішера-Снедекора з густиною
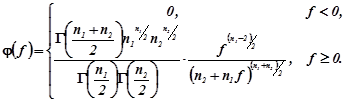 (4.3.2)
(4.3.2)
Розподіл F
Фішера-Снедекора однозначно визначається двома параметрами ![]() (додаток 1.14).
(додаток 1.14).
Математичне сподівання та дисперсія випадкової величини ![]() відповідно дорівнюють
відповідно дорівнюють
![]() ,
(4.3.3)
,
(4.3.3)
![]() .(4.3.4)
.(4.3.4)
Розподіл F
Фішера-Снедекора називають ще ![]() -розподілом.
-розподілом.
5. Статистичні оцінки параметрів розподілу
Нехай необхідно вивчити кількісну ознаку X генеральної сукупності. І нехай відомий вигляд розподілу цієї кількісної ознаки. Необхідно знайти параметри цього розподілу за статистичними даними вимірювань або спостережень.
Приклад 3.1.Якщо відомо наперед, що ознака генеральної сукупності розподілена нормально, то необхідно оцінити параметри 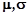 нормального розподілу.
нормального розподілу.
Приклад 3.2.Якщо відомо наперед, що ознака генеральної сукупності має розподіл Пуассона, то необхідно оцінити параметр 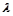 цього розподілу.
цього розподілу.
Нехай ![]() значення кількісної ознаки X
, які одержані в результаті n
спостережень. Від серії до серії спостережень, взагалі кажучи, одержуються різні значення
значення кількісної ознаки X
, які одержані в результаті n
спостережень. Від серії до серії спостережень, взагалі кажучи, одержуються різні значення ![]() . Тому останні мають розглядатися як значення випадкових величин
. Тому останні мають розглядатися як значення випадкових величин ![]() . Щоб знайти точкову
оцінку (точкова оцінка виражається одним числом) невідомого параметра (знайти наближенне значення) необхідно знайти функцію цих випадкових величин, значення якої при їх конкретних значеннях
. Щоб знайти точкову
оцінку (точкова оцінка виражається одним числом) невідомого параметра (знайти наближенне значення) необхідно знайти функцію цих випадкових величин, значення якої при їх конкретних значеннях ![]() було б значенням точкової оцінки невідомого параметра розподілу.
було б значенням точкової оцінки невідомого параметра розподілу.
Отже, статистичною точковою оцінкою невідомого параметра теоретичного розподілу називають функцію випадкових величин![]() .
В подальшому точкова статистична оцінка буде називатися просто статистичною оцінкою.
.
В подальшому точкова статистична оцінка буде називатися просто статистичною оцінкою.
Нехай q
- параметр теоретичного розподілу і ![]() його статистична оцінка. Статистична оцінка називається незміщеною,
якщо її математичне сподівання дорівнює значенню параметра при будь-якому об’ємі вибірки, тобто якщо
його статистична оцінка. Статистична оцінка називається незміщеною,
якщо її математичне сподівання дорівнює значенню параметра при будь-якому об’ємі вибірки, тобто якщо
![]() ,
,
і зміщеною якщо
![]() .
.
Використання зміщеної оцінки приводить до систематичних похибок одного знаку. Цього немає при використанні незміщеної оцінки.
Але незміщена оцінка не завжди дає необхідну точність визначення значення параметра теоретичного розподілу. Для цього необхідно, щоб вона була ефективною, а при великих об’ємах вибірок і умотивованою. Статистична оцінка називається ефективною
, якщо при заданному об’ємі вибірки має найменшу можливу дисперсію. Статистична оцінка є умотивованою
, якщо при ![]() по ймовірності прямує до параметра теоретичного розподілу. Якщо дисперсія незміщенної оцінки при
по ймовірності прямує до параметра теоретичного розподілу. Якщо дисперсія незміщенної оцінки при ![]() прямує до нуля, то така оцінка є умотивованою.
прямує до нуля, то така оцінка є умотивованою.
При малих об’ємах вибірки точкова оцінка може значно відрізнятися від значення параметра теоретичного розподілу. З цієї причини при малих об’ємах вибірок користуються інтервальними оцінками.
Інтервальною називають оцінку, яка визначається двома числами – кінцями інтервала. Інтервальна оцінка дозволяє встановити точність та надійність оцінок.
Нехай ![]() значення оцінки
значення оцінки ![]() для конкретної вибірки.
для конкретної вибірки.
![]() тим точніше
визначає значення параметра q
, чим менша абсолютна різниця
тим точніше
визначає значення параметра q
, чим менша абсолютна різниця ![]() . Нехай d
0 -
деяке число. Ймовірність
. Нехай d
0 -
деяке число. Ймовірність
![]() (1)
(1)
називається надійністю
оцінки ![]() . Рівність (1) можна переписати у вигляді
. Рівність (1) можна переписати у вигляді
![]() ,
,
![]() .
.
Виходить, що ймовірність того, що випадковий інтервал ![]() покриває невідоме значення параметра q
дорівнює g
.
Такий інтервал називається довірчим
. Отже, інтервальна оцінка визначається довірчим інтервалом та надійністю. Чим менша надійність, тим вужчий довірчий інтервал, і навпаки. На практиці надійність задається близькою да 1
. Найбільш часто задають надійності 0.95
,0.99
і 0.999
.
покриває невідоме значення параметра q
дорівнює g
.
Такий інтервал називається довірчим
. Отже, інтервальна оцінка визначається довірчим інтервалом та надійністю. Чим менша надійність, тим вужчий довірчий інтервал, і навпаки. На практиці надійність задається близькою да 1
. Найбільш часто задають надійності 0.95
,0.99
і 0.999
.
6.Статистичні оцінки чисельних характеристик дискретних розподілів
Нехай X дискретна випадкова величина із розподілом
![]() .(1.2)
.(1.2)
Множина значень випадкової величини X є генеральною сукупністю і вважається відомою.
Приклад 4.1.1. Кількість очок, яка випадає при киданні несиметричного кубика є дискретною випадковою величиною з розподілом
![]()
з відомими значеннями та невідомими ймовірностями.
Нехай потрібно знайти математичне сподівання ![]() випадкової величини X
(яке в математичній статистиці називається генеральним середнім
і позначається
випадкової величини X
(яке в математичній статистиці називається генеральним середнім
і позначається ![]() ) та дисперсію
) та дисперсію ![]() (генеральну дисперсією
(генеральну дисперсією
![]() ). Для цього здійснюють вибірку об’єму n
.
). Для цього здійснюють вибірку об’єму n
.
Статистичною оцінкою генерального середнього є випадкова величина
![]() ,(1.3)
,(1.3)
де ![]() – дискретна випадкова величина – кількість значень
– дискретна випадкова величина – кількість значень ![]() у вибірці. Вона може набувати значень від 0
до n
. Статистична оцінка
у вибірці. Вона може набувати значень від 0
до n
. Статистична оцінка![]() є незміщенною (
є незміщенною (![]() ), ефективною та умотивованною.
), ефективною та умотивованною.
Доведення
. Якщо вважати, що вибірка здійснюється по одному, то випадкову величину ![]() можна також представити як суму випадкових величин
можна також представити як суму випадкових величин ![]() - варіанта при
- варіанта при ![]() -вийманні, кожна з яких має розподіл, який співпадає з розподілом випадкової величини
-вийманні, кожна з яких має розподіл, який співпадає з розподілом випадкової величини ![]() :
:
![]()
Тому для математичного сподівання випадкової величини ![]() можна записати
можна записати
![]()
З врахуванням того, що випадкові величини ![]() мають однаковий розподіл з випадковою величиною
мають однаковий розподіл з випадковою величиною ![]() можна записати, що
можна записати, що
![]() ,
,
і, як наслідок,
![]() .
.
Отже, статистична оцінка ![]() є незміщенною.
є незміщенною.
Дисперсії випадкових величин ![]() однакові. Якщо вони обмежені, то згідно теореми Чебишева (3.9.2.1
однакові. Якщо вони обмежені, то згідно теореми Чебишева (3.9.2.1
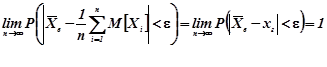 ,
,
а це означає, що ![]() по ймовірності збігається до генерального середнього, що, у свою чергу, означає, що
по ймовірності збігається до генерального середнього, що, у свою чергу, означає, що ![]() є ефективною статистичною оцінкою генерального середнього.
є ефективною статистичною оцінкою генерального середнього.
Випадкова величина (вибіркова дисперсія)
![]() (1.4)
(1.4)
є зміщенною (![]() ) статистичною оцінкою дисперсії дискретної випадкової величини X
– генеральної дисперсії. Тому для генеральної дисперсії використовується “виправлена” вибіркова дисперсія
) статистичною оцінкою дисперсії дискретної випадкової величини X
– генеральної дисперсії. Тому для генеральної дисперсії використовується “виправлена” вибіркова дисперсія
![]() ,(1.5)
,(1.5)
яка є незміщенною (![]() ), ефективною та умотиванною.
), ефективною та умотиванною.
Різниця між вибірковою та “виправленною” вибірковою дисперсіями при достатньо великому об’ємі вибірки мала. На практиці користуються “виправленною” дисперсією , якщо приблизно ![]() .
.
Для оцінки середньоквадратичного відхилення генеральної сукупності (в цьому випадку - дискретної випадкової величини X ) використовують “виправлене” середньоквадратичне відхилення вибірки
![]() ,(1.6)
,(1.6)
яка є незміщенною (![]() , sz
– середньоквадратичне відхилення генеральної сукупності), ефективною та умотивованною.
, sz
– середньоквадратичне відхилення генеральної сукупності), ефективною та умотивованною.
Статистичними оцінками ймовірностей ![]() є відносні частоти
є відносні частоти
![]() ,
,
які є незміщенними (![]() ), ефективними та умотивованими.
), ефективними та умотивованими.
Довірчі інтервали ймовірностей ![]() обчислюються за формулами
обчислюються за формулами
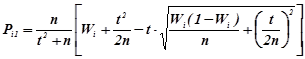 ,(1.7а)
,(1.7а)
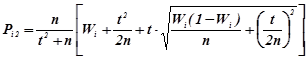 .(1.7b)
.(1.7b)
Значення змінної t
(різне для кожного i
) знаходиться з умови ![]() , де
, де ![]() - інтеграл Лапласа,
- інтеграл Лапласа,![]() - надійність відносної частоти
- надійність відносної частоти ![]() як статистичної оцінки ймовірності pi
.
як статистичної оцінки ймовірності pi
.
Приклад 1.2. Несиметричний кубик кинули 80
разів і при цьому шість очок випало 16
разів. Знайти довірчий інтервал для невідомої ймовірності ![]() з надійністю 0.9
з надійністю 0.9
Розв’язування
. За умовою задачі ![]() . Відносна частота
. Відносна частота ![]() .Значення змінної t
знаходиться рівняння
.Значення змінної t
знаходиться рівняння
![]() . Розв’язок рівняння
. Розв’язок рівняння ![]() . За формулами (4.1.6а) та (4.1.6b)
. За формулами (4.1.6а) та (4.1.6b)
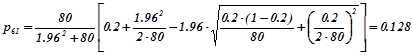 ,
,
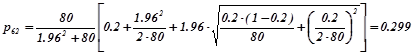 .
.
Отже, довірчий інтеграл для оцінки невідомої ймовірності ![]()
![]() з надійністю 0.9
з надійністю 0.9
7. Метод максимальної правдоподібності
Метод максимальної провдоподібності використовуються для знаходження статистичних оцінок параметрів розподілів випадкових величин (як дискретних, розподіл яких задається аналітичним виразом, так і неперервних випадкових величин).
Нехай X
– випадкова величина з розподілом (якщо вона дискретна) або густиною розподілу ймовірностей (якщо вона неперервна) ![]() , який (яка) однозначно визначається параметром
, який (яка) однозначно визначається параметром![]() , і який невідомий. Для його визначення здійснюється n
експериментів. Результати кожного з експериментів є випадковими величинами
, і який невідомий. Для його визначення здійснюється n
експериментів. Результати кожного з експериментів є випадковими величинами ![]() . Очевидно, що розподіли цих випадкових величин співпадають з функцією
. Очевидно, що розподіли цих випадкових величин співпадають з функцією ![]() випадкової величини X
. Експерименти незалежні, тому за теоремою множення ймовірностей незалежних подійможна записати
випадкової величини X
. Експерименти незалежні, тому за теоремою множення ймовірностей незалежних подійможна записати
![]() .
.
Функція
![]() (2.1)
(2.1)
називається функцією максимальної правдоподібності
. Точка ![]() , в якій функція максимальної правдоподібності досягає максимуму є значенням статистичної оцінки
, в якій функція максимальної правдоподібності досягає максимуму є значенням статистичної оцінки ![]() параметра розподілу
параметра розподілу ![]() . Така статистична оцінка називається оцінкою найбільшої правдоподібності
.
. Така статистична оцінка називається оцінкою найбільшої правдоподібності
.
Функції ![]() та
та ![]() досягають максимуму в одинакових точках. Тому замість точки максимуму функції
досягають максимуму в одинакових точках. Тому замість точки максимуму функції ![]() шукають точку максимуму функції
шукають точку максимуму функції ![]() , що значно зручніше. З математичного аналізу відомо, що точку максимума функції можна знайти за таким алгоритмом:
, що значно зручніше. З математичного аналізу відомо, що точку максимума функції можна знайти за таким алгоритмом:
1) знаходять похідну і прирівнюють до нуля: ![]() ;
;
2) розв’язують одержане рівняння і знаходять екстремальні точки ![]() ;
;
3) знаходять другу похідну ![]() ; якщо друга похідна в екстремальній точці від’ємна, то така точка є точкою максимума функції, якщо додатня, то – мінімуму.
; якщо друга похідна в екстремальній точці від’ємна, то така точка є точкою максимума функції, якщо додатня, то – мінімуму.
Методом максимальної правподібності одержані важливі для практики результати:
1) статистична оцінка параметра ![]() розподілу Пуассона
розподілу Пуассона
![]() ;(2.2)
;(2.2)
2) статистична оцінка параметра p біноміального розподілу є
![]() ,(2.3)
,(2.3)
n1 кількість експериментів у першій серії, X1 - кількість успіхів; : n2 кількість експериментів у другій серії, X2 - кількість успіхіву другій серії;
3) статистичною оцінкою параметра ![]() експоненціального розподілу є обернена величина до вибіркового середнього:
експоненціального розподілу є обернена величина до вибіркового середнього:
![]() .(2.4)
.(2.4)
Якщо розподіл випадкової величини однозначно визначається не одним параметром, а декількома, то функція максимальної правподобності є функцією багатьох змінних:
![]() .
.
В цьому випадку для знаходження точок максимуму необхідно розв’язати систему нелінійних рівнянь
 (2.5)
(2.5)
Саме цим користуються для знаходження статистичних оцінок параметрів нормального розподіл у теорії похибок вимірювання фізичних величин.
8. Теорія похибок вимірювання фізичних величин
Кількісні результати при спостереженнях одержують, як правило, шляхом вимірювання. Якщо істинне значення деякої фізичної величини a
, а в результаті вимірювання одержане значення x,
то похибка вимірювання визначається як різниця між ними: ![]() . Розрізняють три види похибок: промахи, систематичні похибки та випадкові похибки.
. Розрізняють три види похибок: промахи, систематичні похибки та випадкові похибки.
Промахи виникають через грубе порушення умов вимірювання (неправильні дії лаборанта, несправність вимірювальної аппаратури, різка зміна зовнішніх умов) і зазвичай характеризуються порівняно великими похибками.
Систематичні похибки є результатом впливу не врахованих факторів (підвищена температура, електромагнітні завади, тощо) або недоліками вимірювальних приладів (похибка градуювання, недосконалість методу вимірювання) Промахи та систематичні похибки можуть бути виявлені і враховані як при обробці вимірювань, так і при організації вимірювань. Але як би не були добре організовані вимірювання, завжди залишається багато не врахованих факторів, вплив яких приводить до випадкових похибок .
8.1 Основна гіпотеза
Випадкові похибки є результатом дії великої кількості різних факторів , кожна з яких вносить малу похибку, і жодна з них не має домінуючого впливу (похибки зумовлені домінуючими факторами можна віднести до систематичних похибок). У відповідності до теореми Ляпунова є всі підстави вважати , що похибка є випадковою величиною D
з нормальним розподілом (це суть основної гіпотези
).Ця величина може приймати значення похибки ![]() . Є також всі підстави вважати, що відхилення результатів вимірювання рівноймовірні в обидві сторони від істинного значення фізичної величини. Тому математичне сподівання випадкової похибки
. Є також всі підстави вважати, що відхилення результатів вимірювання рівноймовірні в обидві сторони від істинного значення фізичної величини. Тому математичне сподівання випадкової похибки ![]() , а значить її густина розподілу та інтегральна функція матимуть вигляд
, а значить її густина розподілу та інтегральна функція матимуть вигляд
![]() ,(6.1.1)
,(6.1.1)
![]() .(6.1.2)
.(6.1.2)
Результати вимірювання фізичної величини є випадковою величиною X . Якщо похибка вимірювання розподілена нормально, то і розподіл випадкової величини X є нормальним:
![]() (6.1.3)
(6.1.3)
з математичним сподіванням, яке дорівнює істинному значенню a
фізичної величини, та дисперсією ![]() . Результат окремого вимірювання є елементом з нескінченної множини можливих результатів вимірювань в одинакових умовах (такі вимірювання називають рівноточними
). Нескінченна множина значень випадкової величини X
є генеральною сукупністю з нормальним законом розподілу, середньоарифметичне значення якої дорівнює математичному сподіванню, яке, в свою чергу, дорівнює істинному значенню фізичної величини. Це означає, що для одержання істинного значення фізичної величини необхідно виконати нескінченну кількість вимірювань. Але на практиці кількість вимірювань обмежена, і тому знайти істинне значення фізичної величини у результаті вимірювань принципово неможливо. Можна лише поставити задачу знайти наближене значення фізичної величини і оцінити її похибку. А ця задача за основною гіпотезою зводиться до знаходження статистичних оцінок параметрів нормального розподілу.
. Результат окремого вимірювання є елементом з нескінченної множини можливих результатів вимірювань в одинакових умовах (такі вимірювання називають рівноточними
). Нескінченна множина значень випадкової величини X
є генеральною сукупністю з нормальним законом розподілу, середньоарифметичне значення якої дорівнює математичному сподіванню, яке, в свою чергу, дорівнює істинному значенню фізичної величини. Це означає, що для одержання істинного значення фізичної величини необхідно виконати нескінченну кількість вимірювань. Але на практиці кількість вимірювань обмежена, і тому знайти істинне значення фізичної величини у результаті вимірювань принципово неможливо. Можна лише поставити задачу знайти наближене значення фізичної величини і оцінити її похибку. А ця задача за основною гіпотезою зводиться до знаходження статистичних оцінок параметрів нормального розподілу.
8.2 Статистичні оцінки параметрів нормального розподілу
Результати вимірювання фізичної величини є випадковою величиною X . Якщо похибка вимірювання розподілена нормально, то і розподіл випадкової величини X є нормальним
![]() (6.2.1)
(6.2.1)
з математичним сподіванням ![]() , яке у математичній статистиці називають генеральним середнім і позначають
, яке у математичній статистиці називають генеральним середнім і позначають ![]() , та дисперсією
, та дисперсією ![]() ( у матстатистиці
( у матстатистиці ![]() ).
).
Методом максимальної правдоподібності можна довести, що точковими статистичними оцінками параметрів ![]() нормального розподілу (6.2.1) є:
нормального розподілу (6.2.1) є:
![]() ,(6.2.2)
,(6.2.2)
![]() ,(6.2.3)
,(6.2.3)
Оцінка (6.2.3) є зміщеною і тому статистичною оцінкою параметра ![]() є корінь квадратний із “виправленної” дисперсії (1.4) – “виправлене” середньоквадратичне відхилення:
є корінь квадратний із “виправленної” дисперсії (1.4) – “виправлене” середньоквадратичне відхилення:
![]() .(6.2.4)
.(6.2.4)
Довірчий інтервал
![]() (6.2.5)
(6.2.5)
покриває невідоме значення ![]() математичного сподівання із надійностю (ймовірністю)
математичного сподівання із надійностю (ймовірністю) ![]() . Параметр
. Параметр ![]() знаходиться як розв’язок рівняння
знаходиться як розв’язок рівняння ![]() ,
, ![]() - інтеграл Лапласа. Величина
- інтеграл Лапласа. Величина
![]() (6.2.5a)
(6.2.5a)
характеризує точність оцінки (6.2.2). З її використанням довірчий інтервал можна записати у вигляді
![]() (6.2.5b)
(6.2.5b)
Приклад 6.2.1. Випадкова величина має нормальний параметр з відомим середньоквадратичним відхиленням ![]() . Знайти довірчі інтервали для оцінки невідомого математичного сподівання по вибірковому середньому
. Знайти довірчі інтервали для оцінки невідомого математичного сподівання по вибірковому середньому ![]() , якщо об’єм вибірки
, якщо об’єм вибірки ![]() і задана надійність оцінки
і задана надійність оцінки ![]() .
.
Розв’язування . Згідно (6.2.5) довірчий інтервал для оцінки математичного сподівання нормального розподілу є
![]()
Параметр ![]() задовольняє рівнянню
задовольняє рівнянню ![]() . Розв’язок рівняння З
. Розв’язок рівняння З ![]() . Точність оцінки математичного сподівання
. Точність оцінки математичного сподівання ![]() . Довірчий інтервал для оцінки математичного сподівання
. Довірчий інтервал для оцінки математичного сподівання ![]() з надійністю 0.9
з надійністю 0.9
Якщо параметр ![]() невідомий, то довірчий інтервал, який покриває
невідомий, то довірчий інтервал, який покриває ![]() з надійністю
з надійністю ![]() , матиме вигляд
, матиме вигляд
![]() .(6.2.6)
.(6.2.6)
Параметр ![]() є розв’язком рівняння
є розв’язком рівняння ![]() ,
, ![]() - густина розподілу Стьюдента,
- густина розподілу Стьюдента,
![]() (6.2.6a)
(6.2.6a)
точність оцінки (6.2.2) за Стьюдентом.
Приклад 6.2.2. Кількісна ознака генеральної сукупності розподілена нормально. Для вибірки об’єму ![]() знайдено вибіркове середнє
знайдено вибіркове середнє ![]() та “виправлене” середньоквадратичне відхилення
та “виправлене” середньоквадратичне відхилення ![]() .Знайти довірчий інтервал для оцінки математичного сподівання з надійністю
.Знайти довірчий інтервал для оцінки математичного сподівання з надійністю ![]() .
.
Розв’язування . Згідно (2.6) довірчий інтервал, який необхідно знайти,
![]() ,
,
Параметр ![]() задовільняє рівнянню
задовільняє рівнянню ![]() . При
. При ![]() розв’язок рівняння
розв’язок рівняння ![]() . Точність оцінки математичного сподівання за Стьюдентом
. Точність оцінки математичного сподівання за Стьюдентом ![]() . Отже, довірчий інтервал для оцінки математичного сподівання
. Отже, довірчий інтервал для оцінки математичного сподівання ![]() з надійністю 0.9
з надійністю 0.9
Нехай ![]() , де
, де ![]() визначається рівністю
визначається рівністю ![]() . Якщо
. Якщо ![]() , то довірчий інтервал
, то довірчий інтервал
для оцінки середньоквадратичного відхилення нормального розподілу з надійністю ![]() має вигляд
має вигляд
![]() .(6.2.7a)
.(6.2.7a)
Значення q знаходиться як розв’язок рівняння
![]() ,(6.2.8a)
,(6.2.8a)
де ![]() ,
, ![]() .
.
Якщо ![]() , то довірчий інтервал
, то довірчий інтервал
![]() ,(6.2.7b)
,(6.2.7b)
а значення q знаходиться як розв’язок рівняння
![]() .(6.2.8b)
.(6.2.8b)
Функція
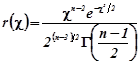 (6.2.9)
(6.2.9)
густина розподілу величини “хі”
![]() .(6.2.10)
.(6.2.10)
Приклад 6.2.3. Кількісна ознака генеральної сукупності розподілена нормально. Для вибірки об’єму ![]() знайдено “виправлене” середньоквадратичне відхилення
знайдено “виправлене” середньоквадратичне відхилення ![]() .Знайти довірчий інтервал для оцінки середньоквадратичного відхилення із надійністю
.Знайти довірчий інтервал для оцінки середньоквадратичного відхилення із надійністю ![]() .
.
Розв’язування
. При ![]() та
та ![]() розв’язок рівняння (6.2.8a)
розв’язок рівняння (6.2.8a) ![]() . Згідно із (2.7a) довірчий інтервал, який шукається у задачі
. Згідно із (2.7a) довірчий інтервал, який шукається у задачі
![]() .
.
Приклад 6.2.4. Кількісна ознака генеральної сукупності розподілена нормально. Для вибірки об’єму ![]() знайдено “виправлене” середньоквадратичне відхилення
знайдено “виправлене” середньоквадратичне відхилення ![]() . Знайти довірчий інтервал для оцінки середньоквадратичного відхилення із надійністю
. Знайти довірчий інтервал для оцінки середньоквадратичного відхилення із надійністю ![]()
Розв’язування
. При ![]() та
та ![]() розв’язок рівняння (6.2.8b)
розв’язок рівняння (6.2.8b) ![]() . Згідно із (2.7b) довірчий інтервал, який шукається у задачі
. Згідно із (2.7b) довірчий інтервал, який шукається у задачі
![]() .
.
8.3 Порядок обробки вимірювань
У теорії похибок вибіркове середнє ![]() позначають як
позначають як ![]() ; її точність
; її точність ![]() при відомому
при відомому ![]() - як
- як ![]() , де
, де
![]() - середня похибка;(6.3.1)
- середня похибка;(6.3.1)
її точність по Стьюденту ![]() - як
- як ![]() .
.
При обчисленні ![]() та s зручно користуватися формулами
та s зручно користуватися формулами
![]() ;(6.3.2)
;(6.3.2)
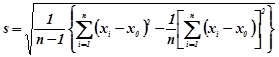 (6.3.3)
(6.3.3)
де ![]() – довільна стала (умовний нуль
), яку вибирають заокругленним числом, близьким до
– довільна стала (умовний нуль
), яку вибирають заокругленним числом, близьким до ![]() .
.
Остаточний результат вимірювання прийнято записувати у вигляді ![]() . У класичній теорії похибок
це означає, що істинне значення фізичної величини покривається довірчим інтервалом
. У класичній теорії похибок
це означає, що істинне значення фізичної величини покривається довірчим інтервалом ![]() з надійністю
з надійністю ![]() (
(![]() - функція ймовірності). У статистиці малих вибірок (мікростатистиці)
це означає, що істинне значення фізичної величини покривається довірчим інтервалом
- функція ймовірності). У статистиці малих вибірок (мікростатистиці)
це означає, що істинне значення фізичної величини покривається довірчим інтервалом ![]() з надійністю (ймовірністю)
з надійністю (ймовірністю) ![]() - (
- (![]() значення густини розподілу Стьюдента у точці
значення густини розподілу Стьюдента у точці ![]() ). При великій кількості вимірювань (
). При великій кількості вимірювань (![]() ) надійності довірчих інтервалів класичної теорії похибок та мікростатистики практично співпадають.
) надійності довірчих інтервалів класичної теорії похибок та мікростатистики практично співпадають.
Приклад 6.3.1.Приклад обробки рівноточних вимірювань, результати яких наведені у наступній таблиці:
| i | |||
1 2 3 4 5 6 7 8 9 10 11 12 |
18338 18316 18325 18341 18332 18319 18313 18329 18310 18322 18330 18314 |
18 -4 5 21 12 -1 -7 9 -10 2 10 -6 |
324 16 25 441 144 1 49 81 100 4 100 36 |
| 49 | 1321 |
![]()
За формулами (3.2), (3.3), (3.1)
![]() ,
, 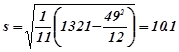 ,
, ![]()
Остаточно
![]() .
.
У класичній теорії похибок це означає, що істинне значення фізичної величини покривається інтервалом ![]() з надійністю
з надійністю ![]() . У мікростатистиці надійність цього довірчого інтервалу менша:
. У мікростатистиці надійність цього довірчого інтервалу менша:![]() (при
(при ![]() ). Із збільшенням довірчого інтервалу його надійність збільшується:
). Із збільшенням довірчого інтервалу його надійність збільшується:
надійність довірчого інтервалу
![]()
дорівнює ![]() у класичній теорії похибок і
у класичній теорії похибок і ![]() у мікростатистиці.
у мікростатистиці.
Якщо вимірювання фізичної величини відбувається при різних умовах, з використанням різних методик та обладнання, то говорять про нерівноточні
вимірювання. При обробці нерівноочних вимірювань, кожному вимірюванню приписується певна вага, яка , як правило, задається цілими числами.Найменш надійному вимірювання приписують найменшу вагу (наприклад, ![]() ), а решту вимірюванням приписуть вагу тим більшу, чим надійніші вимірювання.
), а решту вимірюванням приписуть вагу тим більшу, чим надійніші вимірювання.
Зручно розглядати вагу вимірювання як повторювання вимірювання, тобто вважати, що одне вимірювання з вагою ![]() рівноцінне
рівноцінне ![]() вимірювань з одиничною вагою, що сприяє зменшенню середньої похибки у
вимірювань з одиничною вагою, що сприяє зменшенню середньої похибки у ![]() разів (6.3.1). Обробка нерівноточних вимірювань здійснюється аналогічно до рівноточних з тією лише різницею, що формули для
разів (6.3.1). Обробка нерівноточних вимірювань здійснюється аналогічно до рівноточних з тією лише різницею, що формули для ![]() мають вигляд:
мають вигляд:
![]() ;(6.3.4)
;(6.3.4)
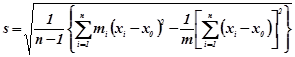 (6.3.5)
(6.3.5)
![]() (6.3.6)
(6.3.6)
де ![]() (n
– кількість нерівноточних вимірювань).
(n
– кількість нерівноточних вимірювань).
Приклад 6.3.2.Приклад обробки нерівноточних вимірювань, результати яких наведені у наступній таблиці:
| i | |||||
1 2 3 4 5 6 7 8 |
236.4 241.6 242.0 240.7 237.4 239.5 243.8 242.5 |
1 3 1 5 3 5 3 5 |
-3.6 1.6 2.0 0.7 -2.6 -0.5 3.8 2.5 |
-3.6 4.8 2.0 3.5 -7.8 -2.5 11.4 12.5 |
12.96 7.68 4.00 2.45 20.28 1.25 43.32 31.25 |
| 26 | 20.3 | 123.19 |
![]() .
.
За формулами (3.4), (3.5), (3.4)
![]() ;
; ![]() ;
; ![]() .
.
Отже, у підсумку ![]()