Матричные игры

СОДЕРЖАНИЕ: ТЕМА: «МАТРИЧНЫЕ ИГРЫ» СОДЕРЖАНИЕ ВВЕДЕНИЕ …. ...…3 1.ТЕОРИЯ ИГР... 3 2.ТЕОРИЯ МАТРИЧНЫХ ИГР … 4

ТЕМА: «МАТРИЧНЫЕ ИГРЫ»

СОДЕРЖАНИЕ

ВВЕДЕНИЕ…………………………………………………………….……………………...…3

1.ТЕОРИЯ ИГР...………………………………………………………………………………3

2.ТЕОРИЯ МАТРИЧНЫХ ИГР……………………………………………………………....4

3.АНТАГОНИСТИЧЕСКИЕ ИГРЫ………………………………………………………….6

ЗАКЛЮЧЕНИЕ………………………………………………………………………………….9

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ……………………………………………10

ВВЕДЕНИЕ

Математическая теория игр является составной частью исследования операций. Она применяется в различных областях человеческой деятельности, таких как экономика и менеджмент, промышленность и сельское хозяйство, военное дело и строительство, торговля и транспорт, связь и т.д.

Зачастую человек осуществляя какую-либо деятельность, сталкивается с проблемой принятия решения в условиях множества факторов, влияющих на само решение. Эффективней всего в подобных случаях пользоваться матричными играми, которые помогают упростить сложившуюся ситуацию и полностью оценить важность каждого фактора.

Принятие решения в условиях неопределенности – это одна из задач теории оптимальных решений. Для решения подобных вопросов разработаны специальные математические методы, которые рассматриваются в теории игр.

1. ТЕОРИЯ ИГР

Теория игр впервые была систематически изложена Дж. фон Нейманом и О. Моргенштерном в 1994 г., хотя отдельные исследования в этой области публиковались ещё в 1920 годах. Нейман и Моргенштерн написали книгу, которая содержала в основном экономические примеры, т.к. описать конфликт легче в числовой форме. После второй мировой войны всерьез теорией игр заинтересовались военные, т.к. увидели в ней аппарат для исследования стратегических решений. Затем внимание снова переключилось на экономические проблемы. Сейчас ведется большая работа, направленная на расширение сферы применения теории игр.

Теория игр – это теория математических моделей, интересы участников которых различны, причем они достигают своей цели различными путями. Столкновение противоположных интересов участников приводит к возникновению конфликтных ситуаций. Необходимость анализировать такие ситуации была причиной возникновения теории игр, задачей которой является выработка рекомендаций к рациональным действиям участников конфликта.

Чтобы исключить трудности, возникающие при анализе конфликтных ситуаций и в результате наличия многих факторов, строится упрощенная модель ситуации. Такая модель называется игрой. Конфликтная ситуация в игровой модели развивается по определенным правилам. Примерами таких игр являются хорошо известные нам шахматы, шашки и карточные игры.

Различают три виды причин неопределенности результата игры:

1. Комбинаторные (наиболее распространенным примером являются шахматы). Особенностью этого вида выступает разнообразие развития игры, что влечет за собой не возможность предсказания её результатов.

2. Влияние различных факторов (чаще встречается в азартных играх, такой как рулетка). Здесь исход игры зависит от случайных причин.

3. Стратегические: неопределенность результата игры состоит в отсутствии информации о действиях противника и его стратегии.

2. ТЕОРИЯ МАТРИЧНЫХ ИГР

Теория матричных игр позволяет нам рассматривать и с легкостью решать задачи принятия решений в ситуациях с несколькими участниками, когда значение целевой функции для каждого зависит также и от решений, принимаемых остальными участниками. Поэтому важная роль в матричных играх отводится конфликтам и совместным действиям.

Характерная черта всякого общественного, социально-экономического явлений состоит множественности и многосторонности интересов и в наличии сторон, выражающих эти интересы. Классическим примером подобной ситуации является столкновение интересов покупателя и продавца, т.е когда на рынок выходят несколько производителей, обладающих достаточной силой для воздействия на цену товара. Более сложные ситуации возникают при наличии объединений и коалиции лиц на рынке, участвующих в столкновении интересов, например, когда ставки заработной платы определяются союзами или объединениями предпринимателей, при анализе результатов голосования в парламенте.

Конфликт может возникнуть из-за различия целей, которые отражают не только несовпадающие интересы, но и многосторонние интересы одного и того же лица. Например, разработчик экономической политики обычно преследует множество целей, согласуя противоречивые требования, такие как рост объемов производства, повышение доходов. Так же конфликт может проявиться не только в результате сознательных действий участников, но и как результат действий тех или иных стихийных сил (ярким примером данного вида являются «игры с природой»). Данные случаи конфликтом могут встретиться как в социологии, так и в психологии, биологии, политологии, военном деле. Самыми простыми примерами матричных игр являются карточные и спортивные игры.

Каждая модель социально-экономического явления должна отражать черты конфликта, т.е. описывать:

множество заинтересованных сторон (в теории матричных игр их называют игроками, т.е. сторонами, участвующими в конфликте. Так же их называют субъектами, сторонами, участниками).
возможные действия каждой из сторон, именуемые стратегиями или ходами. («Ход» - выбор одного из предложенных правилами игры действий; «стратегия» - план, по которому игрок совершает выбор в любой ситуации и т.д.)
интересы сторон, представленные функциями выигрыша (платежа) для каждого из игроков («выигрыш» - исход конфликта).

В теории матричных игр предполагается, что функция выигрыша и множества стратегий, доступна и известна каждому из игроков, т.е. каждый игрок знает свою функцию выигрыша и набор имеющихся в его распоряжении стратегий, а также функций выигрыша и стратегий все остальных игроков, и в соответствии с этой информацией организует свое поведение.

Классификация игр

Различные виды игр можно классифицировать по числу игроков, числу стратегий, свойствам функции выигрыша, возможности предварительных переговоров и взаимодействия между игроками в ходе игры.

В зависимости от числа игроков различают игры с двумя, тремя и более участниками. В теории оптимизации представлены игры как с одним игроком, так и с бесконечным числом игроков.

Согласно другому принципу классификации – по количеству стратегий – различают конечные и бесконечные игры. В конечных играх игроки располагают конечным числом возможных стратегий. Сами стратегии в конечных играх нередко называются чистыми стратегиями. Соответственно, в бесконечных играх игроки имеют бесконечное число возможных стратегий. Так в примере с продавцом и покупателем каждый из игроков может назвать любую устраивающую его цену и количество продаваемого (покупаемого) товара.

Третий способ классификации – по свойствам функций выигрыша (платежных функций). Особым случаем в теории игр является ситуация, когда выигрыш одного из игроков равен проигрышу другого (т.е. прямой конфликт между игроками). Подобные игры называют играми с нулевой суммой или антагонистическими играми. Примерами данных игр являются игры в орлянку. Прямой противоположностью играм такого типа являются игры с постоянной разностью, в которых игроки и выигрывают, и проигрывают одновременно. Между этими крайними имеются множество игр с ненулевой суммой, где имеются и конфликты, и согласованные действия игроков.

В зависимости от возможности предварительных переговоров между игроками различают кооперативные и некооперативные игры. Игра называется кооперативной, если до начала игры игроки образуют коалиции и принимают взаимообязывающие соглашения о своих стратегиях. А игры, в которых игроки не могут координировать свои стратегии, называются некооперативными. Необходимо отметить, что все антагонистические игры могут служить примером некооперативных игр.

3. АНТАГОНИСТИЧЕСКИЕ ИГРЫ

Антагонистические игры являются разновидностью матричных игр, в которых выигрыш одного игрока равен проигрышу другого. Их ещё называют играми с нулевой суммой.

Наиболее часто приводимым примером игр с ненулевой суммой является игра «Дилемма заключенного». Суть игры состоит в том, что два преступника ожидают приговора суда за содеянное. Адвокат конфиденциально предлагает каждому из преступников облегчить его участь, если он сознается и даст показания против сообщника, которому грозит угодить в тюрьму за совершенное преступление на 10 лет. Если никто не сознается, то обоим угрожает заключение на определенный срок (например, 1 год) по обвинению в незначительном преступлении. Если сознаются оба то преступника, то, с учетом чистосердечного признания, им обоим грозит попасть в тюрьму на 5 лет. Каждый заключенный имеет на выбор 2 стратегии: не сознаться или сознаться, выдав при этом сообщника.

Обобщим выше сказанное: 1 игрок – сознаться или не сознаться и 2 игрок – сознаться или не сознаться. В итоге можно получить следующую матрицу «выигрышей» для обоих игроков:

Решение антагонистических игр

Основным допущением при решении данных игр является то, что каждый игрок стремится обеспечить себе максимально возможный выигрыш при любых действиях партнера.

В игре могут участвовать как два игрока (её называют парной), так и множество. Но наибольшее практическое значение имеют парные игры, в которых участников обозначают за A и B. Простейшим видом стратегической игры – игра двух лиц с нулевой суммой (т.е. сумма выигрышей сторон равна нулю).

Игра состоит из двух ходов: игрок A выбирает одну из своих возможных стратегий ( i = 1, 2, …, m ), а игрок B выбирает стратегию ( j = 1, 2, .., n ), причем каждый участник делает выбор в полной ситуации незнании выбора другого игрока. В результате выигрыши и каждого из игроков удовлетворяют соотношению

, откуда если , имеем .

Цель игрока – максимизировать функцию , а игрока В – минимизировать эту же функцию. Каждый из игроков может выбирать одну из переменных, от которых зависит значение функции. Если игрок А выбирает некоторую из стратегий , то это может влиять на значение функции . Влияние на величину значения является неопределенным, а определенность имеет место только после выбора, например, игроком B переменной (при этом определяется другим игроком).

Пусть , тогда составим матрицу:

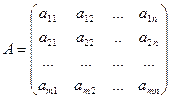Строки матрицы соответствуют стратегиям , столбцы – стратегиям . Матрица А называется матрицей игры, а элемент матрицы – выигрыш игрока А , если он выбрал стратегию , а игрок B выбрал стратегию .

Пусть игрок А выбрал некоторую стратегию , тогда в худшем случае он получит выигрыш, равный . Поэтому предвидя такую возможность, игрок А должен выбрать ту стратегию, которая позволит максимизировать его минимальный выигрыш : . Величина - гарантированный выигрыш игрока А – называется нижней ценой игры, а стратегия , обеспечивающая получение - максиминной.

Игрок В , выбирая стратегию, исходит из следующего принципа: при выборе некоторой стратегии его проигрышнее превысит максимального из значений элементов -го столбца матрицы, т.е. меньше или равен . Рассматривая множество для различных значений , игрок В выбирает такое значение , при котором его максимальный проигрыш минимизируется: . Величина называется верхней ценой игры, а соответствующая выигрышу стратегия - минимаксной.

Фактический выигрыш игрока А при разумных действиях обоих участников ограничен нижней и верхней ценой игры. Если эти выражения будут равны, т.е. , то выигрыш игрока А – вполне определенное число, значит игра называется вполне определенной, а выигрыш – значением игры и равен элементу матрицы .

Вполне определенные игры называют играми с седловой точкой. Элемент в матрице такой игры является одновременно минимальным в строке , максимальным в столбце и называется седловой точкой.

Седловой точке соответствуют оптимальные стратегии игроков, их совокупность – это решение игры, которое обладает следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то для другого отклонение от его оптимальной стратегии не может быть выгодно.

Точка называется седловой из-за формы графика функции выигрыша в точке , которая напоминает седло, убывая при изменении одной из переменных и возрастая при изменении другой переменной.

Необходимо отметить, что в случае, если цена антагонистической игры равна 0, игра называется справедливой.

Задача: определить верхнюю и нижнюю цены для игр, заданных платежными матрицами А и В:

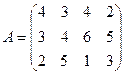и .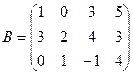

Решение: минимальное значение в строках матрицы А равны соответственно 2,3,1. Максимальное значение из них равно 3. Следовательно, - нижняя цена игры, которой соответствует матрица , равна 3.

Для определения (верхней цены игры) найдем максимальные значения элементов в столбцах матрицы. По столбцам имеем: 4, 5, 6, 5. Следовательно, .

Для матрицы составляем аналогично и :

и .

Таким образом, - цена игры. Решение данной игры состоит в выборе игроком стратегии , при этом выигрыш составит не меньше 4, а для игрока стратегия , позволяющая ограничить проигрыш числом 3.

Игровые системы, содержащие седловую точку, имеют заранее известное решение, т.к. каждый из игроков применяет свою оптимальную стратегию. Решение игры, матрицы которой не содержат седловой точки (т.е. ), довольно затруднительно. Каждый из игроков, применяя минимаксную стратегию, хочет обеспечит себе выигрыш ( не превышающий ) и проигрыш (не меньше ). Для каждого из игроков характерен вопрос о максимизации выигрыша и минимизации проигрыша. Поэтому поиски данного решения состоят в том, что игроки применяют несколько стратегий, причем их выбор осуществляется случайным образом, т.е. смешенной стратегией.

ЗАКЛЮЧЕНИЕ

Теория игр – математический метод изучения оптимальной стратегии в играх. Несмотря на то, что предмет обладает несколько несерьезным названием, он имеет множество экономических приложений и это знание может помочь в оценке многих ситуаций. Теория игр позволяет оценивать игровые стратегии участников и выбрать лучший из предлагаемых вариантов.

Именно теория матричных игр позволяет нам рассматривать и с легкостью решать задачи принятия решений в ситуациях с несколькими участниками, когда значение целевой функции для каждого зависит также от решений принимаемых остальными участниками. Поэтому важную роль в матричных играх отводится конфликтам и совместным действиям.

Теория матричных игр широко нашла свое применение для анализа проблем микроэкономики, а также и в других сферах.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике / Под ред. А.В. Сидоровича. – М.: Издательство «Дело и Сервис», 2004. – с. 368
Кузнецов Ю.Н., Кузубов В.П., Волощенко А.Б. Математическое программирование. – М.: Высшая школа, 1980. – с. 300
Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр. – М.: Книжный дом «Университет», 1998. – с. 304

Скачать архив с текстом документа