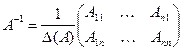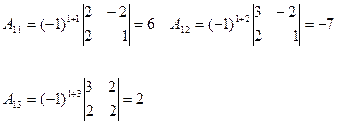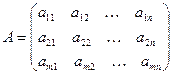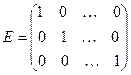Матрицы и определители 3

СОДЕРЖАНИЕ: МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН Рудненский индустриальный институт ДИСТАНЦИОННОЕ ОБРАЗОВАНИЕ МАТЕМАТИКА ЮНИТА № 1 Матрицы и определители.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РЕСПУБЛИКИ КАЗАХСТАН

Рудненский индустриальный институт

ДИСТАНЦИОННОЕ ОБРАЗОВАНИЕ

МАТЕМАТИКА

ЮНИТА № 1

Матрицы и определители.

Рудный 2005

ББК 22.1я73

Авторы : О.Е.Дейвальт

Рецензент: Т.А.Калдыбиев

Рекомендовано к изданию УМС РИИ

Курс: Математика. Базовый курс.

Юнита 1. Матрицы и определители

Юнита 2 Системы линейных уравнений

Юнита 3 Векторная алгебра

Юнита 4 Аналитическая геометрия на плоскости

Юнита 5 Аналитическая геометрия в пространстве

Юнита 6 Предел функции и непрерывность

Юнита 7 Дифференцирование

Юнита 8 Исследование функций и построение графиков

Юнита 9 Неопределенный интеграл.

Юнита 10 Определенный интеграл

Юнита 11 Дифференциальное исчисление функции многих переменных.

Юнита 12 Диффференциальные уравнения (1 и высших порядков) Юнита 13 Дифференциальные уравнения с постоянными коэффициентами.

Юнита 14 Числовые и функциональные ряды

Юнита 15 Ряды Фурье

Юнита 16 Кратные интегралы

Юнита 17 Криволинейные интегралы

Юнита 18 Линейное программирование

Юнита 19 Теория вероятностей

Юнита 20 Математическая статистика

ЮНИТА 1

В данном учебном пособии содержится материал, включающий понятия матриц, определителей, их основных свойств, понятие обратной матрицы. Комплектуется файлом материалов.

Для студентов технических специальностей: 050707, 050709, 050726, 050730, 050729, 050724, 050713, 050718, 050702, 050731, 050901, 050703.

Для студентов экономических специальностей: 050506, 050511

Юнита соответствует типовой образовательной программе

Для внутривузовского использования

© Рудненский индустриальный институт 2005

Содержание

Тематический план………………………………………………………..4

Литература…………………………………………………………………5

Тематический обзор……………………………………………………….6

Глава 1. Матрицы………………………………………………………….7

§1. Основные определения………………………………………………..7

§2. Линейные операции над матрицами…...……………………………..8

§3. Умножение матриц………….…………………………………………8

Глава 2. Определители……………………………………………………10

§1. Определители второго и более высоких порядков……………………………………………………………………10

§2. Свойства определителей………………………………………………12

Глава 3. Обратная матрица. Существование и структура обратной матрицы…………………………………………………………………….13

Файл материалов….………………………………………………………16

Перечень умений…………………………………………………………...21

Тренинг умений…………………………………………………………….23

Задания для самостоятельной работы……………………………………………………………………….30

Глоссарий

Тематический план

Матрицы, действия над матрицами (сложение, умножение на число, умножение матриц).

Определители 2^го и 3^го порядков.

Правило Саррюса (треугольника).

Свойства определителей. Обратная матрица.

Литература

Основная

1. И.В. Виленкин, В.М. Гробер Высшая математика. Ростон-на-Дону, 2002
2. В.Е. Шнейдер, А.И. Слуцкий, А.С. Шумов Краткий курс высшей математики. Т. 1, М. 1978

Дополнительная

3. П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова Высшая математика в упражнениях и задачах. Ч. 1. М. 1980

Тематический обзор

Широкое применение математических методов в самых различных областях науки, техники, экономики и практической деятельности инженеров предъявляет повышенные требования к изучению математических приемов. Особенно важны методы и приемы линейной алгебры, наиболее простые и важные из которых рассматриваются в этом курсе.

В задачи нашего курса входит ознакомление с действиями над матрицами, изучение вычисления определителей, нахождения обратной матрицы.

Глава 1. Матрицы

§1. Основные определения.

МАТРИЦЕЙ размера m^. n называется прямоугольная таблица чисел

,

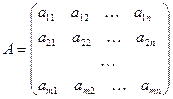содержащая m строк и n столбцов. Каждый элемент матрицы а _ik имеет два индекса: i – номер строки и k – номер столбца. Краткая форма записи матрицы:

А = (а _ik )_{m, n}

Матрица называется КВАДРАТНОЙ порядка n , если она состоит из n строк, и n столбцов.

Матрица размера 1 ^. n называется МАТРИЦЕЙ-СТРОКОЙ , а матрица размера m^. 1 - МАТРИЦЕЙ-СТОЛБЦОМ .

НУЛЕВОЙ матрицей заданного размера называется матрица, все элементы которой равны нулю.

ТРЕУГОЛЬНОЙ матрицей n-го порядка называется квадратная матрица, все элементы которой, расположенные ниже главной диагонали, равны нулю:

.

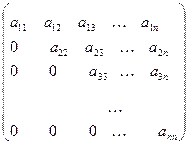ЕДИНИЧНОЙ называется квадратная матрицаn-го порядка, у которой элементы главной диагонали равны единице, а в се остальные элементы – нули:

.

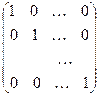Матрицы А = (а _ik )_{m, n} и В = (в _ik )_{m, n} называются РАВНЫМИ , если а _ik = в _ik i = 1,…,m

k = 1,…,n.

§2. Линейные операции над матрицами.

СУММОЙ матриц А = (а _ik )_{m, n} и В = (в _ik )_{m, n} называются матрица А + В = (а _ik + в _ik )_{m, n} .

ПРОИЗВЕДЕНИЕМ матрицы А = (а _ik )_{m, n} на число l называется матрица lА = (lа _ik )_{m, n} .

Для любых матриц одинакового размера и любых чисел l и m выполняются свойства:

1) А + В = В +А 2) А + (В + С) = (А + В) + С

3) А + 0 = А 4) l(mА) = (lm)А

5) l(А + В) = lА + lВ 6) (l + m)А = lА + mА

Докажем свойство 5):

l(А + В) = (l(а _ik + в _ik ))_{m, n} = (lа _ik + lв _ik )_{m, n =} (lа _ik )_{m, n} + lв _ik )_{m, n} = lА + lВ

Доказательство Остальных свойств читатель проведет самостоятельно.

ТРАНСПОНИРОВАННОЙ для матрицы А называется матрица А^Т , строки которой являются столбцами матрицы А, а столбцы – строками матрицы А.

ПРИМЕР 1. Даны матрицы

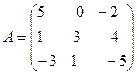и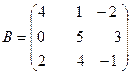

Построить матрицу С = 2А – 3В + А^Т .

РЕШЕНИЕ .

-+

+=.

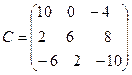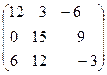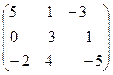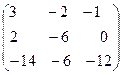§3. Умножение матриц.

ПРОИЗВЕДЕНИЕМ матрицы А = (а _ik )_m,р на матрицу В = (в _ik )_{р , n} называется матрица D размера m^. n с элементами

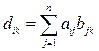
Иными словами, для получения элемента, стоящего в i -ой строке результирующей матрицы и в k -ом ее столбце, следует вычислить сумму попарных произведений элементовi -ой строки матрицы А на k -ый столбец матрицы В.

ПРИМЕР 2. Найти произведение матрицы

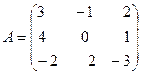на матрицу .

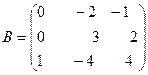РЕШЕНИЕ.

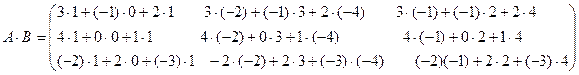
т.е. .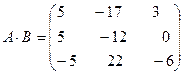

В самом определении произведения матриц заложено, что число столбцов первой матрицы равно числу строк второй. Это – условие согласования матриц при умножении. Если оно нарушено, матрицы перемножить нельзя. Поэтому возможна ситуация, когда произведение А*В существует, а произведение В*А – нет. Кроме того, когда существуют оба произведения, то чаще всего они не совпадают, т.е. в большинстве случаев произведение матриц некоммутативно: А*ВВ*А. Если А, В, С – квадратные матрицы одинакового порядка и Е – единичная матрица того же размера, то справедливы тождества:

Свойство 1) оставим без доказательства ввиду его громоздкости.

Докажем 2):

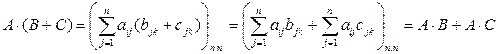
Свойство 3) доказывается аналогично, а 4) следует из определения умножения матриц.

Глава 2. Определители

§1. Определители второго и более высоких порядков.

Пусть 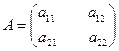- квадратная матрица 2-го порядка.

Определителем 2-го порядка (матрицы а) называется число

D(А) = .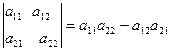

Пример . Вычислить определитель матрицы

.

РЕШЕНИЕ . D(А) = .

Пусть 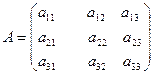- матрица 3-го порядка.

Определителем 3-го порядка (матрицы А) называется число

D(А) =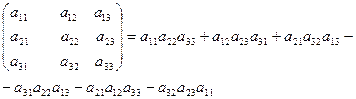

Правило Саррюса (треугольника)

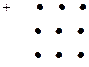
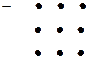
Пример . Вычислить определить

D(А) =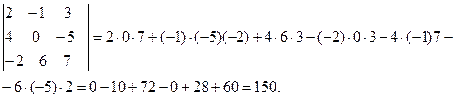

Минором элемента a_ik называется определитель М_ik , составленный из элементов, оставшихся после вычеркивания из матрицы А i -ой строки и k -го столбца.

Алгебраическим дополнением элемента a_ik называется число .

Определителем 3-го порядка (матрицы А) называется сумма произведений элементов первой строки матрицы на их алгебраические допоплнения:

D(А) =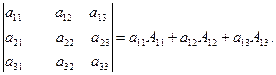

Данную формулу называют разложением определителя по первой строке.

Пример . Вычислить определитель матрицы

.

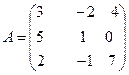Решение . Находим миноры и алгебраические дополнения элементов 1-ой строки матрицы:

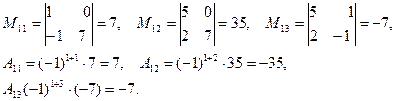
Вычисляем искомый определитель:

D(А) = 3^. 7 + (-2)^. (-35) + 4^. (-7) = 63.

Далее индуктивно вводится понятие определителей более высоких порядков.

Определителем n- го порядка называется число

.

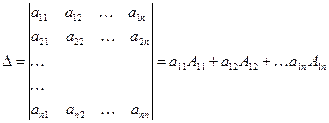§2. Свойства определителей.

Изложенные ниже свойства справедливы для любого n- го порядка. Доказательства будем проводить для n = 3.

1. Определитель не меняется при транспонировании, т.е. D(А^Т ) = D (А). Поэтому в дальнейшем большинство свойств формулируется и доказывается для строк.

2. Если две строки определителя поменять местами, то определитель меняет знак.

3. Если все элементы какой-либо строки (или столбца) равны нулю, то определитель равен нулю.

4. Если все элементы какой-либо строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.

5. Если в определителе две строки (два столбца) одинаковы или пропорциональны, то определитель равен нулю.

6.

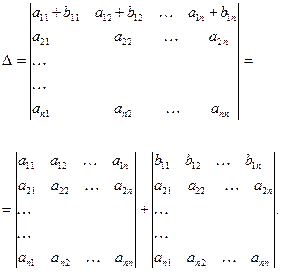
7. Определитель не изменяется, если к элементам какой-либо строки (столбца) прибавить элементы другой строки (столбца), умноженные на одно и то же число.

8. Сумма произведений элементов любой строки (столбца) на свои алгебраические дополнения равна самому определителю. Сумма произведений любой строки (столбца) на алгебраические дополнения другой сроки (столбца) равно 0.

Свойства 1), 2), 8) доказываются непосредственно полным раскрытием определителя. Докажем 3).

Если раны нулю все элементы 1-ой сроки, то по определению

D = 0^. А₁₁ + 0^. А₁₂ + 0^. А₁₃ = 0.

Если нулю равны все элементы другой сроки, то поменяв ее местами с первой (что может повлиять лишь на знак определителя), мы сведем дело к предыдущему. Свойства 4), 6) читатель докажет самостоятельно, используя понятия определителя.

Доказательство 5). Если поменять местами одинаковые строки, то, с одной стороны, определитель не измениться, а с другой – на основании св. 2, он поменяет знак, т.е.

D = -D 2D = 0 D = 0.

Доказательство 7) следует теперь из 6) и 5).

9. Определитель треугольной матрицы равен произведению элементов главной диагонали

.

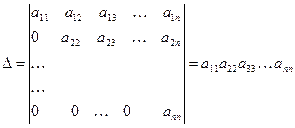Доказательство. Раскладывая D по элементам 1-го столбца, получаем произведение ведущего элемента а₁₁ на определитель такого же вида (n-1)-го порядка с ведущим элементом а₂₂ . Раскладывая этот определитель по элементам 1-го столбца, имеем произведение а₂₂ на определитель такого же вида (n-2)-го порядка. Это значит, что D равен произведению а₁₁ ^. а₂₂ на этот новый определитель. Продолжая этот процесс необходимое число раз, приходим к равенству D = а₁₁ ^. а₂₂ ^. а₃₃ ^. … а_nn .

Сформулируем без доказательств еще один важный факт.

ТЕОРЕМА 1.1. Если А и В – квадратные матрицы одного порядка, то

D(А^. В) = D(А) ^. D(В).

СЛЕДСТВИЕ. D(А^. В) =D(В^. А).

Глава 3. Обратная матрица.

Существование и структура обратной матрицы.

Матрица А^-1 называется обратной к квадратной матрице А, если

А^. А^-1 = А^-1. А = Е.

ТЕОРЕМА 1.2. Для того чтобы матрица А имела обратную, необходимо и достаточно, чтобы она была невыраженной, т.е. чтобы D(А) 0.

ДОСТАТОЧНОСТЬ. Дано: D(А) 0. Докажем, что обратной к матрице А является матрица

.

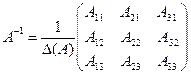В самом деле,

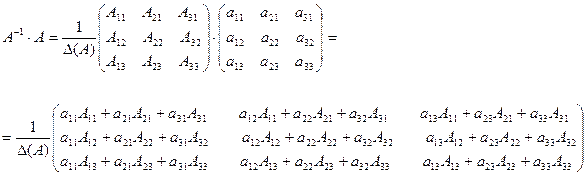
Каждый из элементов главной диагонали равен определителю D(А), ибо представляет собой сумму произведений элементов одной из строк матрицы на свои алгебраические дополнения. Все остальные числа в результирующей матрице равны нулю на основании второй части свойства 8).

Поэтому,

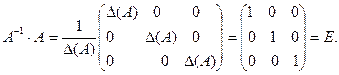
Совершенно аналогично доказывается, что А^. А^-1 = Е.

Это завершает доказательство достаточности.

НЕОБХОДИМОСТЬ . Дано, что матрица А^-1 существует. Надо доказать, что

D(А) 0. Допуска, что D(А) = 0, мы бы получили из равенства А^. А^-1 = Е,

D(А) ^. D(А^-1 ) =DЕ, откуда D(А) ^. D(А^-1 ) = 1, что невозможно, ибо левая часть этого равенства есть 0.

ПРИМЕР . Найти обратную к матрице

.

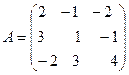РЕШЕНИЕ . Вычисляем алгебраические дополнения всех элементов данной матрицы:

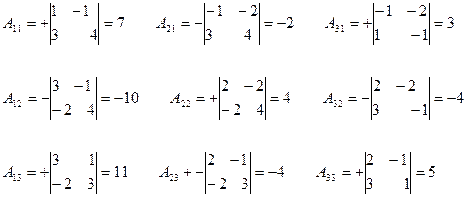
Находим определитель матрицы А:

DА = 2^. 7 +(-1) ^. (-10)+(-2) ^. 11 = 2

Теперь записываем обратную матрицу

.

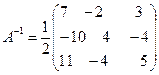ПРОВЕРКА .

=

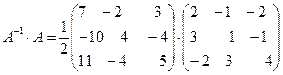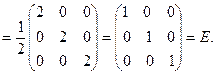
Значит, матрица А^-1 найдена верно.

Файл материалов

Примеры решения задач.

Действия над матрицами (линейные операции над матрицами,

транспонирование матрицы, умножение матриц).

Данной теме посвящены §2,3 главы 1, где изложен теоретический материал и разработаны примеры.

Пример 1 . Найти сумму двух матриц А и В, где

.

Операция сложения двух матриц определена, только если обе матрицы – слагаемые имеют одинаковый порядок. В данном случае матрицы А и В одинакового порядка. Порядок матрицы – это пара чисел, первое из которых m равно числу строк матрицы, а второе n – числу ее столбцов. Матрицы А и В имеют порядок 2^. 4(m =2, n =4).

Матрицы А и В можно сложить. Суммой А+В будет матрица того же порядка, что слагаемые, обозначим ее С.

Элементы с_ij (i = 1,2; j = 1,2,3,4) получаются как суммы элементов матрицы А и В с одинаковыми индексами с_ij = а_ij + b_ij , i = 1,2; j = 1,2,3,4.

Итак, имеем .

Пример 2 . Даны матрицы А и В. Найти матрицу С = 2А + В.

.

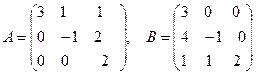Заметим, что наши матрицы – квадратные (число строк равно числу столбцов, это общее число 3 и есть порядок наших матриц). Матрицы А и В – треугольные, у матрицы А под главной диагональю все элементы нулевые. Это свойство матриц исчезнет при их сложении. Чтобы получить матрицу 2А, следует все элементы А умножить на 2.

.

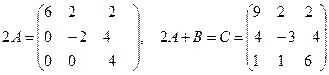Пример 3 . Найти произведение матриц АВ = С, где

.

Для умножения двух матриц их порядки должны быть «согласованы», а именно, число столбцов в первом множителе (матрица А) равно числу строк второго множителя В. В нашем случае обе матрицы квадратные и имеют одинаковый порядок 2. Значит, умножение АВ определено.

Произведение С=АВ будет квадратной матрицей того же порядка. Обозначим ее элементы с_ik , i = 1,2; k = 1,2.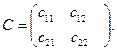

Чтобы получить с₁₁ следует в матрице А выделить первую строку, а в матрице В выделить первый столбец и вычислить их скалярное произведение с₁₁ = 2^. 0+0^. 0=0. Теперь вычислим с₁₂ , для этого выделим в А снова первую строку, а в В – второй столбец, перемножим их соответствующие элементы и сложим.

Далее, , элемент с₂₂ получается при умножении второй строки А и второго столбца В.

с₂₂ = 2^. 2+(-1)^. (-1) = 5.

Запишем теперь матрицу .

Пример 4 . Пусть А и В – матрицы из примера 6. Вычислить произведение ВА=Д, проверить, будут ли матрицы А и В перестановочны.

.

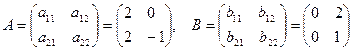Выпишем формулы для вычисления элементов i = 1,2; j = 1,2 матрицы Д:

d₁₁ = a₁₁ b₁₁ + b₁₂ a₂₁ , d₁₂ = b₁₁ a₁₂ + b₁₂ a₂₂ ,

d₂₁ = b₂₁ a₁₁ + b₂₂ a₂₁ , d₂₂ = b₂₁ a₁₂ + b₂₂ a₂₂ .

Подставим в эти формулы числовые значения

d₁₁ = 4, d₁₂ = -2, d₂₂ = 1, и матрица D=ВА имеет вид

Очевидно, АВ ВА, т.е. от перестановки сомножителей произведение изменилось, т.е. матрицы А и В не перестановочны.

Пример 5 . Найти произведение С матрицы А на вектор – столбец .

.

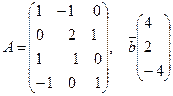Умножение возможно, т.к. вектор можно рассматривать как матрицу, имеющую 3 строки и 1 столбец, а матрица А имеет 3 столбца, и число ее столбцов равно числу строк вектора . Произведение С = А будет иметь порядок 4^. 1, т.е. будет вектором-столбцом с элементами с₁₁ , с₂₁ , с₃₁ , с_41.

с₁₁ = 1^. 4-1^. 2+0 = 2; с₂₁ = 0^. 4+2^. 2-4^. 1 = 0;

с₃₁ = 4+2 = 6; с₄₁ = -4+4 = 0.

.

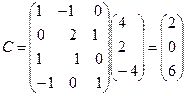Таким образом, если умножение возможно, то произведение матрицы на вектор будет вектором.

Примеры решения задач на вычисление определителей.

Теория изложена в главе 2 §1.

Пример 1 . Вычислить определитель .

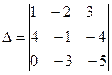
Вычислим по правилу Саррюса

D = 1(-1) ^. (-5)+(-2)(-4)0+4(-3)3-0(-1)3-4(-2)(-5)-(-3)(-4)1=5+0-36+0-40-12=-83.

Пример 2 . Вычислить определитель примера 1 разложением по первой строке.

Найдем алгебраические дополнения.

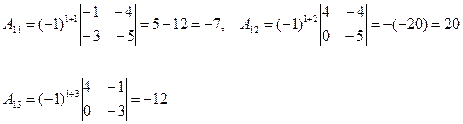
D = 1^. (-7)+(-2)20+3(-12)=-7-40-36=-83.

Пример 3 . Вычислить определитель 4^го порядка.

.

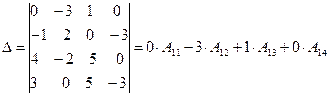Найдем алгебраические дополнения А₁₂ , А₁₃

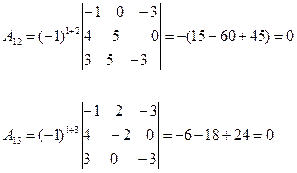
D = 0.

Примеры решения задач на вычисление обратной матрицы.

Теория изложена в главе 3.

Пример 1 . Найти обратную к матрице

Вычислим алгебраические дополнения всех элементов данной матрицы

А₁₁ = +(-4)=-4 А₂₁ = -(-2)=2

А₁₂ = -3 А₂₂ = +1

Найдем определитель D = (А) = 1(-4)-3(-2)=-4+6=2

Проверка

.

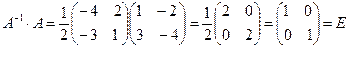Пример 2 . Найти обратную к матрице

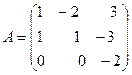
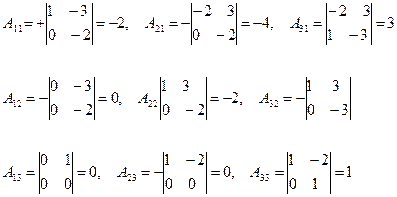
D(А) = -2

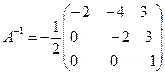
Проверка

.

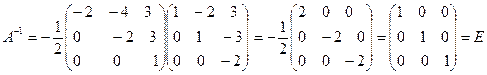Перечень умений.

№ п/п	Умение	Алгоритмы
1	Линейные операции над матрицами. Вычисление С=aА+bВ, где a,b - числа, А,В – заданные матрицы.	1. Определить, имеют ли матрицы А и В одинаковый порядок. Если «да», то перейти к п.2, в противном случае вычислит С нельзя. 2. Умножить все элементы матрицы А на число a aА = (aаij )m, n 3. Умножить все элементы матрицы В на число b bВ = (bbij )m, n 4. Вычислить элементы матрицы С по формулам: сij = aаij + bbij , i = 1,2,…m, j = 1,2…n
2	Умножение матриц. Вычисление произведения матрицы А на В. С = АВ	1. Проверить, совпадает ли число столбцов матрицы А = (аij )m, n с числом строк матрицы В = (bij )n, k («согласованы» ли порядки множителей). Только в этом случае можно умножить А на В. В противном случае вычислить С нельзя. 2. Определить порядок матрицы произведения6 С = (сij )m, k имеет порядок mxk, где m – число строк первого множителя А, k – число столбцов второго множителя В. 3. Вычислить каждый элемент матрицы произведения С по формулам: сij = аi1 b1 j + аi2 b2 j + … + аin bnj i = 1,2, …m, j = 1,2…n. 4. Выписать полученную матрицу С.
3	Вычисление определителей 3го порядка по правилу Саррюса	1. По схеме Саррюса составить произведение трех элементов определителя, взяв по одному из строки и столбца. 2. Вычислить определитель, подсчитав сумму полученных произведений, взяв эти произведения с соответствующим знаком.
4	Вычисление определителей разложением по первой строке	1. Найти миноры Mij элементов первой строки вычеркивая последовательно элементы первой строки и j-ый столбец (j = 1,2 …,n), составляя из оставшихся элементов определители. 2. Найти алгебраические дополнения элементов первой строки А1 j = (-1)1 + j Mij 3. Вычислить определитель 4. D = а11 А11 + а12 А12 +…+ а1 n А1 n

5

Вычисление обратной матрицы

1. Найти алгебраические дополнения элементов матрицы Аij = (-1)i + j Mij 2. Вычислить определитель матрицы D(А) 3. Найти обратную матрицу

Тренинг умений.

Пример выполнения упражнения тренинга на умение 1.

Задание

Вычислить матрицу С = 5А – В, где

.

Решение.

Предварительно заполните таблицу, подобрав к каждому алгоритму конкретное соответствие из данного задания.

№	Алгоритм	Конкретное соответствие данного задания предложенному алгоритму
1	Определить, имеют ли матрицы А и В одинаковый порядок. Если «да», перейти к п.2, в противном случае вычислить С = 5А – В нельзя	Обе матрицы имеют порядок 2. 3 (на первом месте число строк, на втором – число столбцов). Матрицы одного порядка, переходим к п.2.
2	Умножить все элементы А на число 5
3	Умножить все элементы В на (-1)
4	Вычислить элементы матрицы С: сij = 5аij – вij

Решите самостоятельно следующие задачи:

Задача 1.

Даны матрицы А и В. Найти С = 2А + 3В.

.

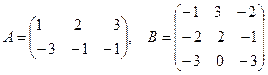Задача 2.

Даны матрицы А и В. Найти С = 3А – 2В.

.

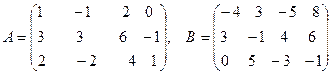Пример выполнения упражнения тренинга на умение 2.

Задание

Даны матрицы А и В. Найти матрицу С = АВ, если возможно.

.

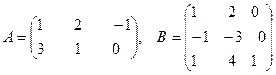Решение.

Предварительно заполните таблицу, подобрав к каждому алгоритму конкретное соответствие из данного задания.

№	Алгоритм	Конкретное соответствие данного задания предложенному алгоритму
1	Проверим, совпадает ли число столбцов матрицы А с числом строк В («согласованы» ли их порядки). В противном случае умножение А на В невозможно.	Матрица А имеет порядок 2. 3, число ее столбцов равно 3, матрица В имеет порядок 3. 3, число столбцов у нее 3, порядки «согласованы», существует произведение А на В С = АВ
2	Определить порядок матрицы произведения: С имеет порядок mxk , где m – число строк А, n – число столбцов В.	Порядок матрицы С будет 2. 3, т.к. матрица А имеет 2 строки, а матрица В имеет 3 столбца С = (сij )23
3	Вычислить каждый элемент матрицы С по формулам: сij = аi1 b1 j + аi2 b2 j + … + аin bnj i = 1,2, …m, j = 1,2…n.	Вычисляем элементы первой строки С: i = 1, j = 1,2,3 с11 = а11 b11 + а12 b21 + а13 b31 = =(1. 1)+2(-1)+(-1) . 1=-2 с12 = а11 b12 + а12 b22 + а13 b32 = =1. 2+2. (-3)+(-1) . 4=-8 с13 =а11 b13 + а12 b23 + а13 b33 = =1. 0+2. 0+(-1) . 1=-1 Вычисляем элементы второй строки: i = 2, j = 1,2,3 с21 =а21 b11 + а22 b21 + а23 b31 = =3. 1+1. (-1)+0. 1=2 с22 =а21 b12 + а22 b22 + а13 b32 = =3. 2+1. (-3)+0. 4=3 с23 =а21 b13 + а22 b23 + а23 b33 = =3. 0+1. 0+0. 1=0
4	Выпишем полученную матрицу-произведение

Решите самостоятельно следующие задачи.

Задача 1.

Найти произведение матриц АВ и ВА, если они существуют.

Сравните матрицы-произведения.

а)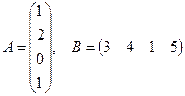

б)

с) .

Задача 2.

Вычислить произведения АВ и ВА.

.

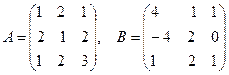Совпадают ли матрицы произведения АВ и ВА?

Задача 3.

Вычислить А³ , где матрица задана:

Указания: найти сначала произведение АА = А² , затем нужно умножить А²

на А,

А³ = А^2. А.

Задача 4 . Найти произведение АВ и сравнить с матрицей ВА.

.

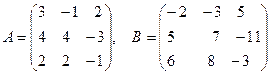Пример выполнения упражнения тренинга на умение 3.

Задание

Вычислить определитель

.

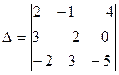Решение.

Предварительно заполните таблицу, подобрав к каждому алгоритму конкретное соответствие из данного задания.

№	Алгоритм	Конкретное соответствие данного задания предложенному алгоритму
1	Перемножить элементы определителя главной диагонали и параллельно главной диагонали построить треугольники, взяв элементы по одному из строки и столбца, сложить их.	Соответствует формуле Саррюса (треугольника) 2. 2. (-5)-1. 0(-2)+3. 3. 4= =-20+48=28
2	Перемножить элементы побочной диагонали и параллельно побочной построив треугольники, затем сложить их, поменяв знак каждого произведения.	-(-2. 2. 4+3. (-1)(-5)+3. 0. 2)= =-(16+15)=1
3	Вычислить определитель, сложив полученные результаты	D=28+1=29 Определитель равен 29.

Решите самостоятельно.

Задача 1 . Вычислить определитель по правилу Саррюса (треугольника)

.

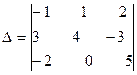Пример выполнения упражнения тренинга на умение 4.

Задание

Вычислить определитель

.

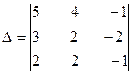Решение.

Предварительно заполните таблицу, подобрав к каждому алгоритму конкретное соответствие из данного задания.

№	Алгоритм	Конкретное соответствие данного задания предложенному алгоритму
1	Вычислить алгебраические дополнения элементов первой строки	Вычеркиваем последовательно элементы первой строки, получаем соответствующие миноры, умножаем на (-1)1+ k
2	Вычислить определитель по формуле D = а11 А11 + а12 А12 + а13 А13	D = 5. 6+4. (-7)-1. 2= =30-28-2 = 0 D = 0

Решите самостоятельно.

Задача 1.

Вычислить определитель .

Задача 2.

Вычислить определитель .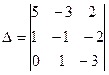

Пример выполнения упражнения тренинга на умение 5.

Задание.

Вычислить обратную матрицу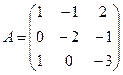

Решение.

Предварительно заполните таблицу, подобрав к каждому алгоритму конкретное соответствие из данного задания.

№	Алгоритм	Конкретное соответствие данного задания предложенному алгоритму
1	Убедится, что обратная матрица существует	Вычислите определитель матрицы и убедитесь, что он не равен нулю D(А) = 6+1+0+4+0-0 = 11 0
2	Найти алгебраические дополнения элементов матрицы А	А11 = 6 А12 = -1 А13 = 2 А21 = -3 А22 = -5 А23 = +1 А31 = 5 А32 = +1 А33 = -2
3	Составить транспонированную матрицу из алгебраических дополнений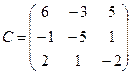
4	Найти обратную матрицу
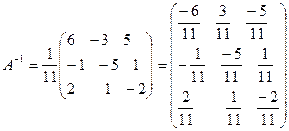5	Убедиться, что обратная матрица найдена верно А-1. А = Е

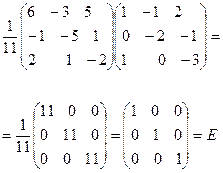Решите самостоятельно.

Вычислить обратную матрицу .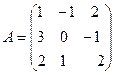

Задания для самостоятельной работы

Самостоятельно решите следующую задачу:

Даны две матрицы

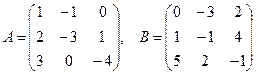
1. Построить матрицу С.
2. Найти определитель матрицы С.
3. Найти матрицу, обратную к матрице С.
4. Найти произведение матриц А и С.

№ вар	С	№ вар	С
1	2А-3В + АТ	11	-2А+В+2АТ
2	А+2В+ВТ	12	-3А+4В-3ВТ
3	-2А-В+2АТ	13	-А+3В+4АТ
4	3А-В+ВТ	14	2А+4В-ВТ
5	А-3В+2АТ	15	3А-В+АТ
6	3В-2А-ВТТ	16	2А+5В-2АТ
7	2А+В-АТ	17	3А-В-3ВТ
8	2В-2А+3ВТ	18	4А+2В-АТ
9	4А+В-2АТ	19	2А+3В+2АТ
10	-2А+4В+ВТ	20	2А-3В-ВТ

ГЛОССАРИЙ

№	Новые понятия	Содержание
1	Прямоугольная матрица порядка mn, обозначаемая	Прямоугольная таблица из mn действительных чисел, где первое число m равно числу строк, а n – числу столбцов матрицы А; коротко матрица А обозначается А = (аik )mn
2	Элементы матрицы	числа аik , из которых состоит матрица; индексы определяют положение элемента в таблице; первый индекс i – номер строки, второй k – номер столбца, на пересечении которых стоит элемент аik
3	Квадратная матрица порядка n	матрица, число строк которой равно числу ее столбцов и равно числу n
4	Главная диагональ квадратной матрицы А	образуется элементами с одинаковыми индексами а11 , а22 , …, аmn
5	Транспонированная матрица	квадратная матрица, элементы которой симметричны относительно главной диагонали, равны аik = аki , i – 1,2,…,m; k= 1,2,…,n
6	Единичная матрица (Е)	квадратная матрица, на главной диагонали которой стоят единицы, а остальные элементы нулевые
7	Произведение матрицы Аmn (порядка mxn) на матрицу Вnk (порядка nxk)	матрица Сmk (порядка mxk), элементы которой вычисляются по формуле: Сij = аi1 b1 j + аi2 b2 j +…+ аin bnj , i = 1,2,…,m; j = 1,2,…,k
8	Определитель квадратной матрицы А	число, которое ставится в соответствие матрице А и вычисляется по ее элементам
9	Алгебраическое дополнение Аij элемента аij	величина Аij = (-1)i+ j Mij , где Mij – определитель порядка (n-1), полученный вычеркиванием i-ой строки и j-го столбца, на пересечении которых стоит элемент аij
10	Вырожденная матрица	матрица, у которой определитель равен нулю
11	Обратная матрица для матрицы А	квадратная матрица А-1 , которая удовлетворяет условию А. А-1 = А-1. А = Е; обратная матрица А-1 существует тогда и только тогда, когда исходная матрица невырожденная, detA 0

Скачать архив с текстом документа